“说理”，撬开数学思维的内核

颜永锵

摘  要：基于核心素养下“说理”的数学课堂不但注重数学知识的重要内涵，而且更侧重培养学生的理性精神。因此，教师应该从凸显知识本真、亲历思动过程、撬开思维内核和拓展知识价值四个方面进行说理、析理、悟理和明理，让学生在“讲理”的思维内生中促使学习更加深入与深刻，让深度学习真正发生！

关键词：“说理”;核心素养;思维内核;深度学习

一、凸显知识本真，溯求“说理”之源

“说理”一个充满灵性的词语，不仅是在课堂上会说、会表达，还应在表达的基础上，在进一步内化知识中触及知识的内核，在明晰数理中直抵数学知识的本质，这样的学习才更有深度。“说理”的核心在于让学生明晰知识的本质属性是什么，进而把握知识的“源”与“流”。

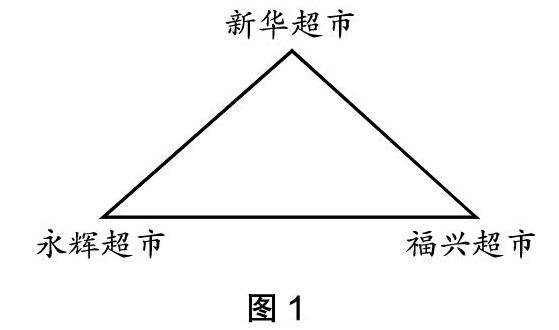
例如《三角形三边关系》这一课，我们知道三角形三边关系的数学本质是“两点之间线段最短”，而这个数学之“理”比较抽象，不易理解。如何让学生基于已有经验感悟这个“理”，用自己的方式来表达这个“理”？教学时基于生活情景设计两个活动，活动一（你看出来了吗）：送货员要将货物从永辉超市运到福兴商场，从永辉超市到福兴商场有几条路，哪条路最近（如图1）？

学生基于已有生活经验判断出由永辉超市直接到福兴商场的路最近。但这个一目了然的“最近”却蕴含着深刻的数学之理，如何凸显呢？此时，教师及时追问：我们一看就知道由永辉超市直接到福兴商场的路最近，这个“最近”同学们是“看”出来的，你们能“想”出来吗？能运用已学过的知识来讲道理吗？活动二（为什么都一样）：从新华超市到福兴商场怎么走最近？从永辉超市到新华商场呢？教师引导学生思考“从上面三次行走路线，你发现了什么共同的地方？为什么这样走最近呢？”，从而明晰了“两点之间线段最短”的道理。那怎样从“两点之间线段最短”引向“三角形任意两条边之和一定大于第三边”呢？这时教师引导学生观察：两条不同路线围成一个什么图形？如果从三角形边的角度去观察，这三条边之间又有怎样的关系呢？三边的关系又蕴藏着一个怎样的“理”？

以“走哪条路最近”这个问题切入，让学生经历从生活的“理”→知识的“理”→数学的“理”逐步内生历程，从直观之“理”走向抽象之“理”，溯求出“三角形三边关系”这一知识的由来，更好地把握知识的本质。可见，只有理解了数理之源，掌握了数理的本质，学生才会真正“讲道理”！

二、亲历思动过程，迸发“说理”之欲

苏霍姆林斯基说：“儿童的智慧在他的手指尖上。”可见，学生要会“读”数学、“说”数学，首先应从“做”数学开始。因此，在教学中教师应有意识地放手让学生边操作边思考，把操作与思维联系起来，让学生在思与动的活动中轻松、愉快地掌握数学知识。

比如在《直角梯形和等腰梯形的認识》教学中，由于直角梯形和等腰梯形都是特殊的梯形，这部分知识学习应基于学生认识一般梯形概念后再进一步深化与延伸。为此，教师引导学生展开以下探究：直接抛出问题“我们已经认识了梯形，那你们认为什么是直角梯形？如果给你一个梯形，你认为怎样操作才会变成直角梯形？”让学生在纸上画一个梯形，剪下来进行操作思考后再呈现学生的操作：在这个梯形剪纸上画一条高，沿着这条高剪开便得出直角梯形。及时叩问：你是怎么想的？能说说道理吗？再进一步追问：除了这条高，还可以怎么剪？有几条呢？能说说无数条的理由吗？最后质疑：如果作两条腰的高，还是直角梯形吗？为什么？通过正反对比，让学生自觉地发现和认识直角梯形的特点：这条高必须与上下底是互相垂直的。

可见，让学生借助动手操作经历知识建构的过程，有效实现了知识与方法的对接，强化了概念的内涵本质，深化了概念的外延，从而引发数学思考，深刻知识之理，迸发学生自觉“说理”之欲望。

三、撬开思维内核，感受“说理”之趣

罗鸣亮老师说过：“撬开学生的嘴说数学的理！”在实际课堂教学中教师都能让孩子表达，让孩子回答，但其往往只关注到浅层次的一问一答，很少有深层次的“溯理”。因此，课堂中我们应进一步深究，引导学生在深究中说理、悟理，这样不但撬开了学生的嘴，而且撬开了学生数学思维的内核。

例如五年级上册《三角形的面积》，教学时直接抛出问题：三角形的面积你们会算吗？在学生回答后及时出示底为8厘米、高为3厘米的等腰三角形，学生列出8×3÷2=12，然后以“知道三角形的面积为什么可以这样计算吗？有没有办法来验证这个答案？”为切入点，让学生主动操作后呈现两种不同的方法，再进一步比较方法的异同点：这两种做法中，三角形的底、高和面积各是怎样变化的？变化过程中，什么变了？什么不变？你是怎么想的？观察一下，底÷2×高，这跟前面讲的公式“底×高÷2”是不一样的，这是怎么回事呢？怎么会与“底×高÷2”不一样呢？“底×高÷2”到底是什么道理？这样通过撬开学生的嘴说“底×高÷2”蕴含着知识之“理”，再让学生深入地研究一下：你能借助两个完全一样的三角形拼成一个什么图形？（平行四边形）从拼成的平行四边形中可以看出“底×高÷2”表示什么？这样的数学臆测过程不仅撬开了学生的嘴，而且撬开了学生数学思维的内核。

通过问题引领、对话交流、思辨提升、追根溯源，引导学生挖掘隐藏在数学知识背后的那些深层次的数学之“理”，从而促进“数学理解”，活化“数学思维”，让学生在新旧知识转化中理通知识脉络，撬开思维内核，感受数学之理！数学之趣！

四、拓展知识价值，感悟“说理”之妙

“拓展，让数学知识更有价值！”数学知识的价值在于引导学生观察和认识周围世界最简单的数量关系，拓展延伸知识的外延，帮助学生不断地运用数学知识发现和解决现实生活问题。

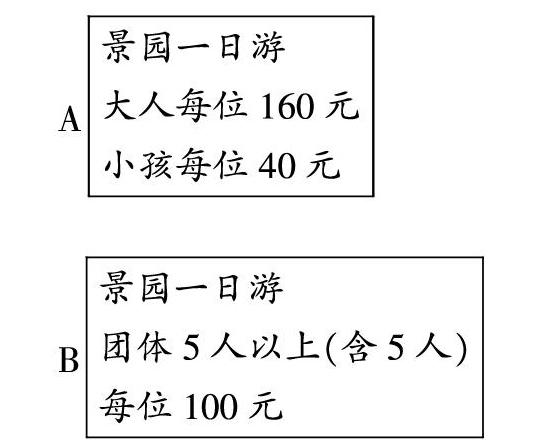
例如在执教五年级上册《旅游费用》一课时，出示这样的问题：（1）4个大人，1个小孩，哪种方案更省钱？（2）2个大人，4个小孩，哪种方案更省钱？

学生根据以上两个问题进行计算比较找出答案，然后诱发学生思考：如果大人和小孩人数相等，该选哪种方案呢？你们能先猜测一下吗？同学的猜测是有依据的，他的猜测对不对，如果不对怎么办？你想用什么方式讲道理？问题到这里已经解决了。但实际教学却不仅仅停留于此，而是顺势而为进一步拓展延伸：从上面的算式中，你又发现了什么？如果是8个大人和8个小孩，该选哪种方案？都是10人呢？20人呢？a（a大于2）个人呢？大家思考一下，为什么大人和小孩的人数相等时，无论选哪种方案都一样呢？同桌互相交流讨论一下，你是怎么想的？学生发现，因为A方案中大人每位160元比B方案中每位100元多60元，而A方案中小孩每位40元比B方案中每位100元少60元，所以刚好抵消掉了。1个大人和1个小孩合起来就是200元。基于这样思考，教师再次引导学生说理：可以举一个算式来说理吗？（160+40）÷2=100，100=100或者160+40=200，100×2=200，200=200，根据A方案我们算出平均每人需要100元，与B方案中每位需要100元一样，所以人数相等，钱数就相等。知识的魅力在于让学生感受到数学之理的奇妙。因此，还需要进一步概括延伸：是不是所有情况都适用呢？我们不妨用大人小孩均为a个人（a大于2）进一步验证一下，你还能讲道理吗？不妨一起算一算：A方案，160a+40a=200a;B方案，100×（a+a）=100×2×a=200a，200a=200a。显然人数相等，钱数就相等。

总之，“说理”的数学课堂应基于学生已有的经验，深入挖掘数学知识的本质，在思动的探究过程中撬开学生数学思维的内核，在知识拓展中促进深度学习真正发生，从而让学生在说理、析理、悟理和明理中有效提升数学核心素养。