教学证据分析的实践样态
周昱城


摘 要:基于证据的教学是“以学生学习为中心”的教学理念的践行,证据的重要性不言而喻。证据有多少价值,能发挥多大的作用,都需要对证据进行分析与挖掘。教学證据分析的实践策略是实现这个目标的手段之一。我们可以用证据链的层层逼近分析法对证据进行分析,最大化发挥其作用,为教学判断与决策提供支撑。
关键词:教学证据;分析;实践样态;证据链
随着时代的发展,科技的进步日新月异,其中信息获取的手段、途径、方式以及信息的价值与以往任何年代相比,其差异都是极大的。当下的儿童在何时运用什么方式获得什么信息或知识,教师很难考证。教育外围的变革对教师的教育教学提出了新的要求。那种“我认为学生……”式的教学前的判断与假设已经不能适应时代的发展,因为它的主观性会让教学迷失方向,行走在错误的道路上。改变现状的方法之一,是让教学立足于证据开展、进行,这就是基于证据的教学。
证据一词无论法律(听到它就让人联想到法律)上还是生活中,都不是一个陌生的词汇。证据是指能够证明某事物的真实性的有关事实或材料。从词汇的释义中可以分析出:(1)证据是事实或材料;(2)证据是真实的;(3)证据与要证明的事物具有相关性,这种相关性是必要且充分的。它们自身的真伪和之间的相互逻辑关系都需要分析与推理。作为指向、为教学服务的证据也具有相同性质与问题。对证据的判断与分析是利用证据开展教学前的必备工作。如何对证据进行甄别、判断与分析,需要研究与实践,笔者在教学中不断学习与探索,下面就结合自己平时的工作,阐述证据链的层层逼近分析法。
一、证据链的层层逼近分析法样态模型
教学目标的确立、起点的把握、方向的判断以及路径的规划都需要证据作为支撑,而首次从学生处收集到的证据往往不能为精准教学提供有价值的信息。这种首次证据与要服务的教学目标状态之间在逻辑上可能存在沟壑。把沟壑的两边联系起来,需要建立一个证据链,即各个证据之间基于反映学生认知水平和能力以及知识结构的逻辑关系而客观形成的链条式关联系统。证据链中前面的链环不能为教师的教学判断提供充分有效的证据,跟进证据的收集分析成为必要,后一个证据链环是对前一个证据链环的补充与推进。证据链得延伸至逼近学生学习的真实状况和教师想要了解的事实内容,为教学决策提供高质量的证据。
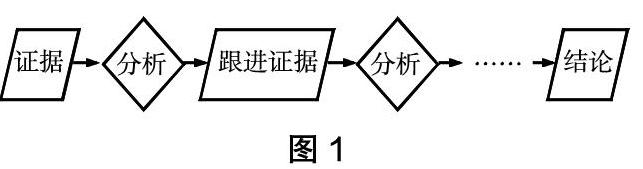
证据链的层层逼近分析模型(如图1):
选取学生中具有代表性的样本作为待分析的证据素材,抽样成功与否决定了后继工作的成败。“如果样本选择恰当,那么这些学生样本的结果能够……在相当程度上,代表所要评估的全体学生中会得出的那种结果”,分析后虽然能得到客观事实,但这些证据又不能为教学判断提供有价值的信息,需要在之后追加证据。接下来为学生提供需要进一步加工的素材,素材的设计必须能延续前面正确的方向深入推进,或者纠偏,使取证指向正确方向,步入正轨。跟进证据的收集,分析层层推进,让证据链一直触及学生认知深处。
二、证据链的层层逼近分析法案例解析
学生,你的困难在哪里?
教学内容是苏教版五年级(下册)第80页《异分母分数加法》。
学习这节课的教学内容时,让学生自主探究后,效果总不是太好。不理想的学习效果背后是什么制约着学生的学习与探究?如果教师有假设的答案,这个假设的答案可靠性是多少,它需要证据;如果教师不武断推论,答案又是什么,它也需要证据。
1. 初始具有代表性的证据分析
教学前让学生完成一份只有一道题的检测试卷,统计学生的解答情况,发现百分之六十几的学生的解答与想法惊人地相似。下面是一份具有代表性的答卷(如图2):
从计算结果的数据特征可以判定学生的计算方法是将分子相加作分子,分母相加作分母。从学生画的图可以推出学生构建的计算方法的知识依据,即学生能理解每个分数的意义,但是没有将两个分数放在统一的背景下去思考,没有意识到两个分数的单位“1”应该是一样的,运算的时候学生只是把每个小正方体作为计量单位,所以将分子与分子、分母与分母直接相加。
通过对学生的答题情况进行分析,可以得到以下两点启示:
(1)学生会进行整数加法,并且会无意识地迁移到分数加法中去;
(2)学生没有意识到整数加法与分数加法之间的区别;
(3)学生没有真正领会加法的本质含义。
这些情况说明教师需要进一步了解学生现有的知识状况以及学习新知的能力水平。
2. 跟进证据的分析
从上面的证据分析得出的结论来看,后面要立足于学生知识的储备状况和解决问题的思考能力两个方面进行调查了解,所以设计了两道学情调查题,一道是启发学生联想与回忆以前学过的知识,另一道是同分母分数加法及其解题过程和思路的呈现。下面是连续跟进调查学生的答题情况(如图3)。
第一问的设置,原本想让学生尽量多地回忆有关学过的分数内容,比如分数的意义、分数单位、单位“1”、同分母分数加减法……哪曾想,学生用“我想到了三年级的初步认识分数”一句话概括了许多内容。虽然如此,但并不影响第二问的解答。学生绘制的图画清晰地表达出计算的想法:因为分母相同,所以只要把分子相加,但却没能说明此时分母不需要相加的原因。学生之所以会这样,原因有两个。其一是以前学的整数加减法的计数单位在其范围内都是统一的,比如13+4表示的是把13个一和4个一合起来,不需要刻意换算,同分母分数加法也是如此。在这个学习背景下的图示讲解只是形式而已,无法触及单位不同及换算相同后才能相加的本质。其二是教师在教学计量单位换算时,并未有意识地将其与计数单位相关内容建立联系,比如“4元+5角”怎样运算?等于9元还是9角?让学生自己明白计量单位不统一就不好直接相加减。
3. 再次跟进证据分析
跟进证据分析后,发现学生原有的知识储备能胜任新知的学习,但是学生没有发现自己构建的计算方法与学过的计算方法不兼容,它们之间存在着矛盾。为了让学生意识到这个矛盾的存在,将问卷聚焦在这个矛盾上,于是笔者又命制了一道用学生的错误思维解答过的同分母加法的题目,激化认知冲突,启发思考,了解学生的思辨能力。
学生能判断出正确的结果,“因为都平均分成了5份,每一份是一样大的”反映出学生意识到分数单位相同才能直接相加,但却没能给出两种算法产生矛盾的解释。(图4)
通过证据链的层层逼近分析,挖掘出学生学习异分母分数加法产生困难的症结:一是完全不知道自己要解决什么问题,不知道异分母加法究竟是什么在相加,比如+表示的是1个加2个;二是没有意识到它们可以相加的本质原因,同分母分数相加是因为分母相同,所以默认了只有相同分数单位才能相加这样的计算前提。这两点促使学生不会把异分母分数加法的运算方法与同分母分数加法的运算方法相联系,而是另外构建了一种运算方法。要想让学生有意识地将两者建立联系,课堂教学决策就必须建立在证据链层层逼近分析得到的结论之上。
证据链层层逼近分析法是教师从学生呈现出的表面现象走入对学生认知深层了解的一个有效手段与方法。在这个方法的实施中,教师需要在“逼近”的进程中洞察学生现状,并据此设计出环环相扣的调查问卷或素材,直至找准学生认知起点。

