从简单到深刻的教学

王佳颖

摘  要：在数学教学中，问题解决作为生活情境教学的重要载体，对学生思维的发展起着至关重要的作用。只有让学生充分理解问题，感悟数学运算产生的必要性，体会多种有效策略解决问题的思路，才能让学生对数学有深层次的理解。

关键词：问题解决;深入教学;思维发展

斯托利亚尔指出：数学教学是数学思维活动的教学。“如何让数学教学由浅入深？如何把简单的内容上得深刻？如何让学生进行深入的数学思维活动，感受数学思维的多维发散？”是数学教学关注的热点问题。

本文以西师版三年级上册《两位数除以一位数》有关比较的问题解决练习课为例，探讨如何把简单的内容上深刻。在教学中，如果仅让学生以机械的计算练习为主，学生将会产生对问题理解不透彻、无法体会数学运算产生的必要性等问题，以致数学教学乏味无趣，缺乏数学味。如果能够改变机械地刷题教学模式，采用以学生的理解为前提，把握数学本质，推动思维的深入，让数学运算自然产生的教学方式，则能够促进学生数学思维的发展。

【片段一】 充分感悟，体会数学运算的作用。

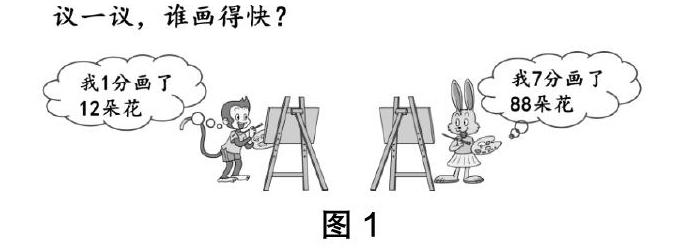
师：能直接比较吗？

生：不能。

师：为什么不能呢？

生：时间不同。

师：时间不同就不能比较了吗？

生：不能，一个是1分钟，一个是7分钟，不公平。

师：那怎么才公平呢？

生：把时间变得一样。

师：也就是说，在时间相同的前提下进行比较，才公平，才有意义。那怎么把时间变得相同呢？

生1：可以都变成7分钟。

生2：还可以变成1分钟。

师：看来有两种思路，这就需要我们进行数学运算了。

生1：让小猴画7分钟，一分钟画12朵，7分钟画12×7=84（朵），再和小兔的7分钟比较，84<87，所以小兔画得快些。

生2：让小兔画1分钟，小兔7分钟画87朵，1分钟平均画87÷7=12（朵）……3（朵）。小兔1分钟画12朵多一点。比较12=12，所以小兔画得快些。

师：小兔1分钟画12朵多一点？怎么看出来的？

生：商12余4，说明比12大，但是还没到13，所以是12朵多一点。

师：12=12，不是相等的意思吗？

生1：虽然都是12，但是此12非彼12。小兔的12，是12多一点，没到13;小猴的12，就是12。虽然算式是相等的，但是意义不同。所以还是能判断出来，小兔画得快。

生2：我觉得可以写成12……4>12，这样就更清楚了。

师：说得都有道理。

师：为了公平比较，把时间变得相同。你们用两种方式把时间变相同，一种是变1分钟，一种是变7分钟。两种计算方式，你更喜欢哪一种呢？

生1：喜欢第一种。乘法好算，不会像除法一样产生余数。

生2：我喜欢第二种，这样我能够清楚地看到，小兔1分钟画多少朵花。

师：只要保证公平地比较，两种方式都是可以的。只是运用除法，有时会遇到余数，要理清余数的含义。

【思考】 教师用层次分明的问题串引导学生深入思考，能够促进学生数学思维能力的发展。由“能直接比较吗？”这个问题引发学生思考，比较的前提是要建立在同一标准下。再由“怎么把时间变相同呢？”这个问题让学生想到把小猴与小兔的时间变得相同的方式有两种，开启思路的大门，让算法多样化。要让学生体会数学运算产生的必要性，数学不是为运算而运算，运算的产生是因为实际需求。“两种计算方式，你更喜欢哪一种呢？”启发学生对比思考每种算法的优缺点，优化算法。

【片段二】发散思维，体会多种解题策略。

师：有什么想法？

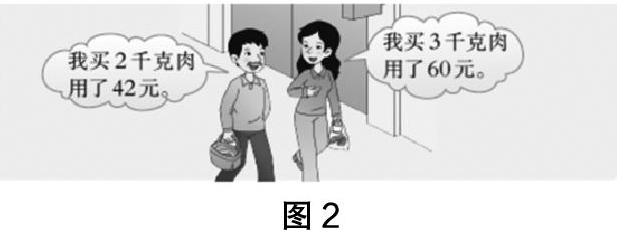
生1：不能直接比较。叔叔买的2千克，阿姨买的3千克，他俩买的重量不同。

生2：应该把它们都变成1千克。

生3：也可以都变成2千克或者3千克。

生4：还可以都变成6千克。

师：听起来方法有点多，咱们一个一个分析。

生1：我觉得把2千克变成3千克，或者把3千克变2千克有点困难，变1千克比较简单。先看看叔叔和阿姨买的肉平均每千克多少钱，再比较。叔叔平均每千克的价钱是42÷2=21（元），阿姨平均每千克的价钱是60÷3=20（元），21>20，所以阿姨买得便宜些。

生2：把2千克变成3千克或者把3千克变成2千克，和变成1千克一样简单，都是两步计算。比如叔叔不变，把阿姨的3千克变成2千克，就要先算阿姨的1千克多少钱，再算3千克多少钱。算式是60÷3=20（元），20×2=40（元），42>40元，所以阿姨买得便宜些。

生3：哦，我懂了，就是先算1千克，再算2千克。那我来补充把3千克变成2千克。阿姨不变，先算叔叔的1千克多少钱，算式是42÷2=21（元），再算3千克的价钱，算式是21×3=63（元），60<63，所以阿姨买得便宜些。

生4：可以都变成6千克。叔叔买2千克是42元，3个2千克就是6千克，所以42+42+42=126（元），阿姨买3千克是60元，2个3千克就是6千克，所以60+60=120（元），126>120，所以阿姨买得便宜些。

师：你们的想法真是太精彩了。可以采用比较1千克的方式，也可以先算1千克，再算几千克后比较，还可以采用多买、买的重量同样多的方式进行比较。老师为你们多样的思考方式点赞！

师：老师有个问题想问大家，小猴画花的题目，可以直接把1分钟变7分钟，或者7分钟变1分钟，一个算式就解决了，但是为什么买肉这道题却多出一步算式呢？

生：7是1的倍数，3不是2的倍数，带小数点的计算，我们还没学。

师：火眼金睛！有倍数关系的，可以一步到位，没有倍数关系的，咱们也可以用学过的知识去解决。

【思考】本题是在比较小猴和小兔画花的基础上，进一步加强在同一标准下的比较计算。小猴的1分钟和小兔的7分钟，是有倍数关系的，可以直接运算转化，再比较。但是叔叔阿姨买肉的2千克与3千克的转化，在学生现有的认知基础上是无法直接运算的，部分学生对此感到困惑，无从下手。因此，分步转化就是解决这道题的关键。在课堂上，学生想到的4种分步转化方法从不同角度精彩地解决了分步转化问题，突破了教学难点。在教学中，教师尊重学生的想法，呈现多种解题策略，充分发散了数学思维。

有关比较类型的问题解决，在教学中是一个既简单又有难度的教学点。学生看到类似“谁多？”“谁快？”等问题时，都知道要进行比较。但是在比较之前，為什么要产生相关的数学运算呢？这个问题，很多学生并没有深入思考。教师的引导，是让学生明白，不在同一个标准下的比较是没有意义的、不公平的。数学运算的产生，是为了得到统一的比较标准，不是为了计算而计算。数学运算是实际需求的必然结果，它能够帮助我们解决问题。而统一比较标准的过程，就是学生深入思考、思维发展的过程，多角度、全面、深入的思考，能够促进学生数学思维能力的有效发展。