层状岩体横观各向同性劣化模型研究

潘洪月，张 丽，宛良朋，王 坤，赵代鹏

(1.中国三峡建设管理有限公司乌东德工程建设部，云南 昆明 651500；2.中国长江三峡集团有限公司科技管理部，北京 100089)

层状岩体作为人类工程活动最密切的地质体之一，岩层是由一系列层间岩石和层面组成的一种天然复合材料。大量试验研究结果都表明，层状岩体的强度、破坏模式[1-3]和变形[4]均具有高度的层面依赖性。此外，大量现场试验研究结果表明，深部洞室开挖后其周边岩体会出现一个损伤松动区，该区域内岩体力学性质会较开挖前明显变差，即开挖引起的应力重分布导致围岩在屈服后的力学性质产生了明显劣化。因此，建立反映深部层状岩体的变形破坏特征及其损伤松动圈内岩体力学参数的劣化规律的力学模型并预测损伤松动圈的范围和深度，成为涉及层状岩体的深部地下工程实践中亟待解决的一个重要课题。

本研究在将层状岩体视作层间岩石与层面组成的复合材料的基础上，分别就层间岩石和层面的力学性质建立相应的力学模型，并考虑横观各向同性条件下弹性参数的劣化对岩体力学性质的影响；最后将该模型应用于乌东德水电站层状岩体洞室群的围岩开挖稳定性分析，并与现场监测结果对比分析，以证明该模型的工程适用性。

1 层状岩体劣化模型

1.1 坐标系

模型将层状岩体视作层间岩石与层面组成的复合材料，分别就层间岩石和层面的力学性质建立相应的力学模型。其中层间岩石力学模型在全局坐标系下建立，层面力学模型在局部坐标系下建立。模型所采用的坐标系如图1所示。图1中，α和β分别为层面走向角和倾向角。α为层面北向夹角，β为层面东向夹角，以此定义层面空间位置。

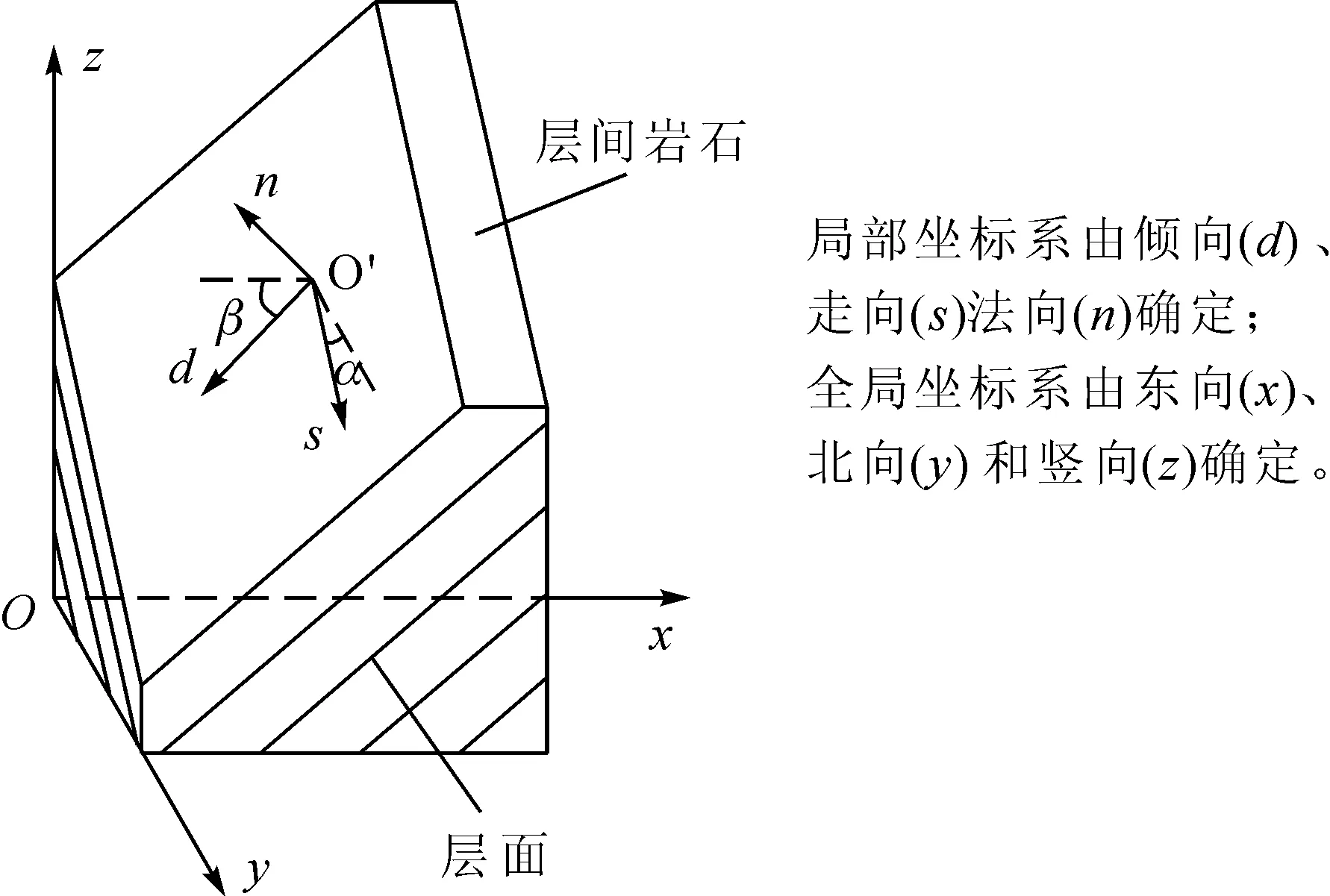
图1 层状岩体坐标系图

1.2 应力-应变关系

横观各向同性条件下在局部坐标空间内的应力-应变关系[5]为

[Δε′e]=[D′][Δσ′]

(1)

式中：[Δε′e]和[Δσ′]分别为局部坐标系下的应变增量和应力增量；[D′]为局部坐标系下的柔度矩阵, 其具体表达式为

(2)

式中：E1和E3分别为平行于和垂直于层面方向的层状岩体的弹性模量；G12=E1/2(1+v12)和G13分别为平行于和垂直于层面方向的层状岩体的剪切模量；v12和v13分别为平行于和垂直于层面方向的层状岩体泊松比。

式(1)可以进一步表达为应力增量由应变增量确定的形式，即

[Δσ′]=[K′][Δε′e]

(3)

式中，[K′]为局部刚度矩阵，等于局部柔度矩阵[D′]的逆矩阵。

全局坐标系下的应力-应变关系为

[Δσ]=[K][Δεe]

(4)

式中：[Δεe]为全局坐标系下的弹性应变增量；[K]为全局坐标系下的刚度矩阵，它可以由下式确定：

[K]=[Q][K′][Q]T

(5)

式中，[Q]为坐标转换矩阵，其表达式为

(6)

式中：l1=cosαcosβ；l2=-sinα；l3=-cosαsinα；m1=sinαcosβ；m2=cosα；m3=sinαsinβ；n1=-sinβ；n2=0；n3=cosβ。

1.3 屈服函数和塑性势函数

层间岩石的屈服函数采用线性Mohr-Coulomb准则(见图2)建立。层间岩石的塑性势函数为剪切屈服函数fms和拉伸屈服函数fmt组成：

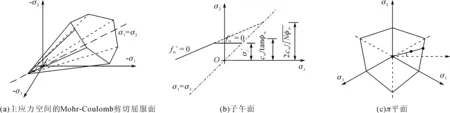
图2 层间岩石的复合屈服准则图

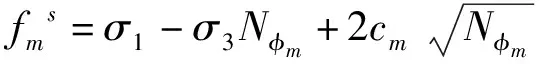
(7)

fmt=σ3-σmt

(8)

式中：σ1和σ3分别为大主应力和小主应力；cm和φm分别为层间岩石的粘聚力和内摩擦角；且Nφm为

(9)

式中，σmt为层间岩石的抗拉强度，其最大值为

(10)

层间岩石的塑性势函数为考虑抗剪和抗拉的复合函数形式(gms和gmt)。剪切塑性势函数gms和拉伸塑性势函数gmt形式如下：

gms=σ1-σ3Nψm

(11)

gmt=σ3

(12)

式中，ψm为层间岩石的剪胀角，且Nψm为

(13)

层面的塑性势函数由剪切屈服函数fjs和拉伸屈服函数fjt组成(见图3)。

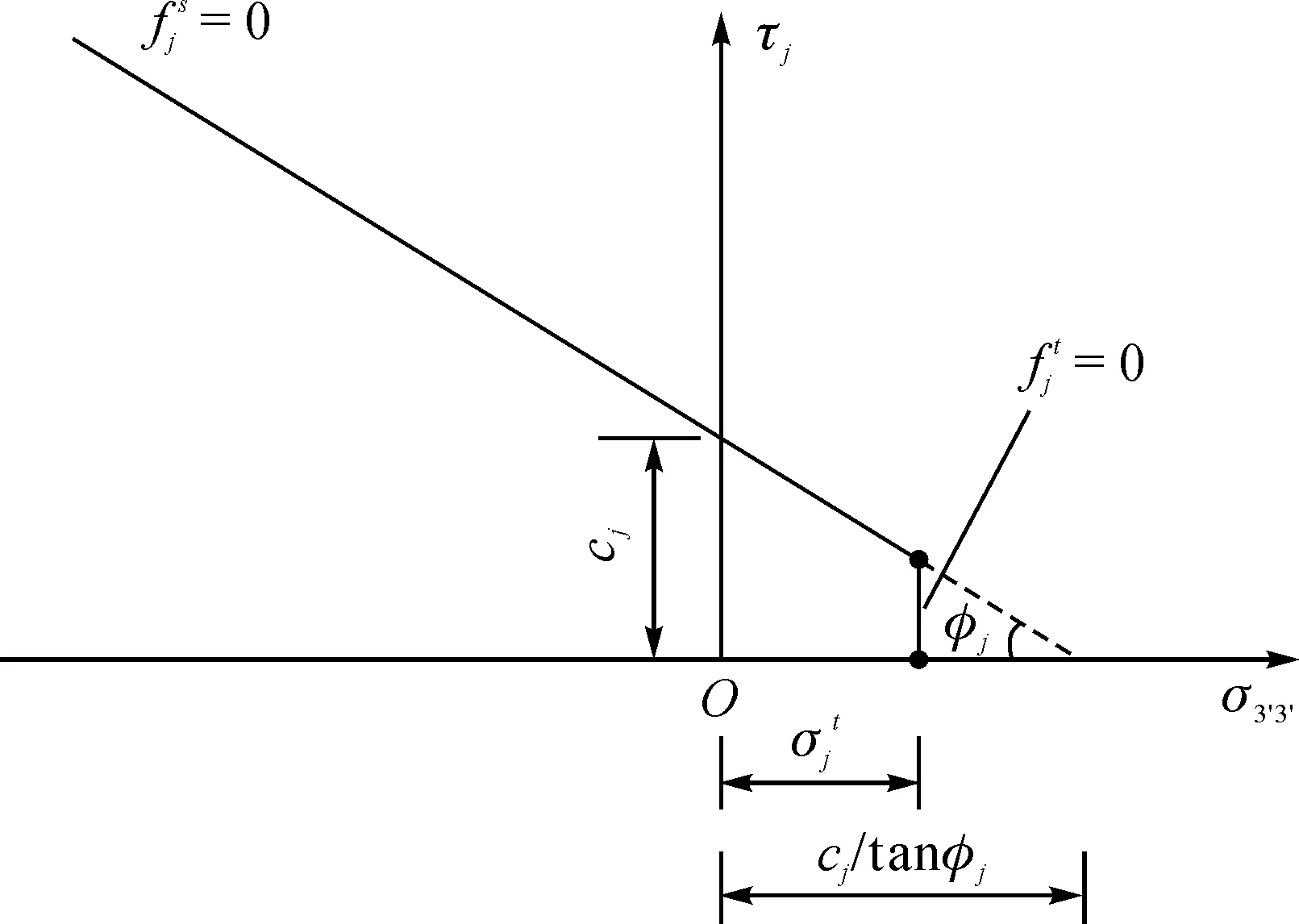
图3 层面的复合屈服准则图

fjs=τj-cj+σ3′3′tanφj

(14)

fjt=σ3′3′-σjt

(15)

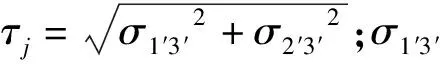
层面的塑性势函数为考虑抗剪和抗拉的复合函数形式(gjs和gjt)。剪切塑性势函数gjs和拉伸塑性势函数gjt形式如下：

gjs=τj+σ3′3′tanψj

(16)

gjt=σ3′3′

(17)

式中，ψj为层面剪胀角。

2 力学参数演化规律

2.1 弹性模量劣化规律

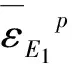
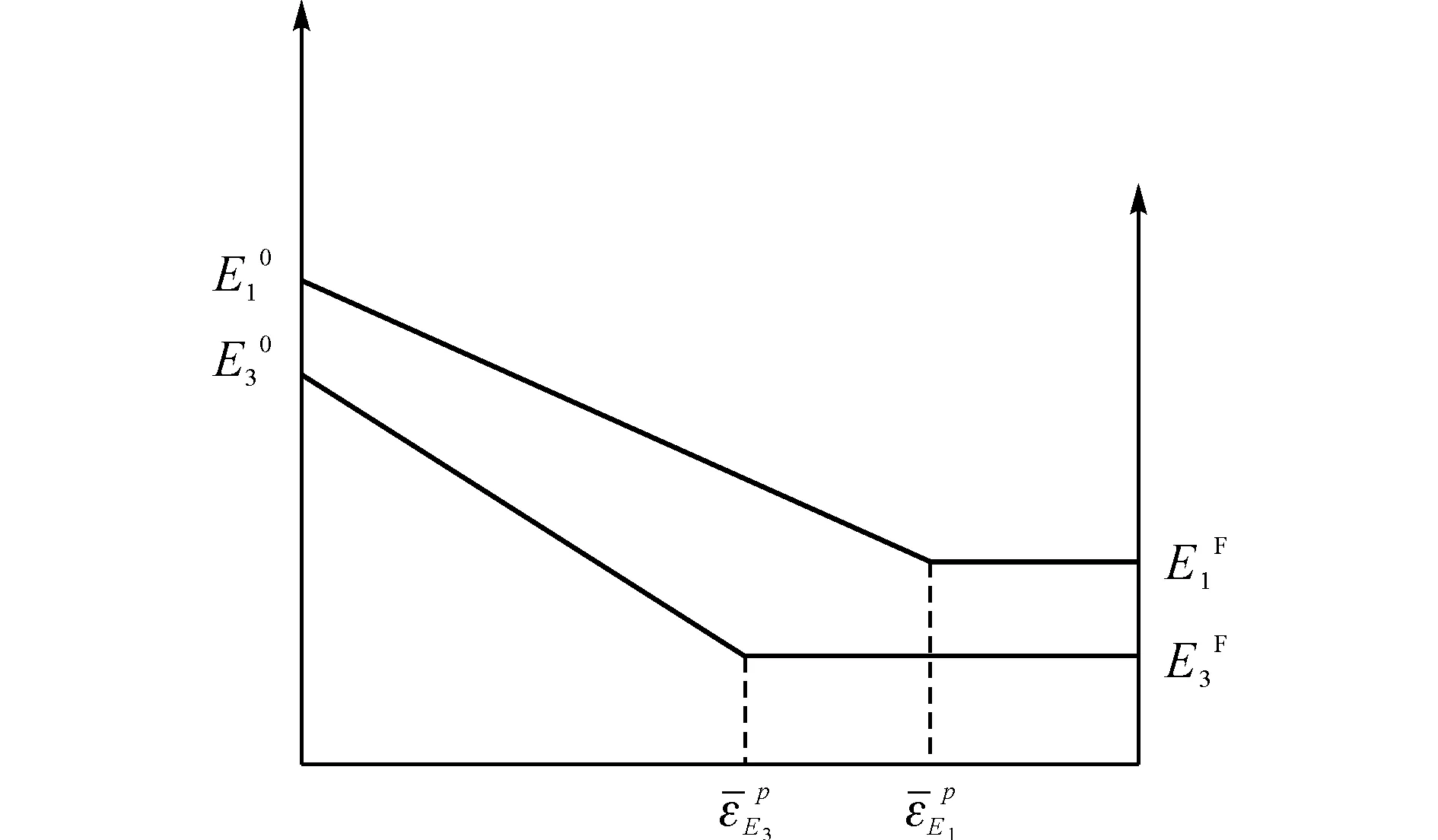
图4 弹性模量随等效塑性应变变化示意图

为有效解决模型中弹性模量劣化极限随意取值导致出现加卸载线相交从而违背Drucker公设的问题，确保岩体弹塑性耦合模型理论的严密性，这里采用Zhang等[6]提出的各向同性同性岩体弹塑性耦合模型的弹模裂化极限取值统一限定条件，即认定和的劣化极限值要满足下式

EF/E0≤ζ

(18)

式中，ζ为临界值，其基于线性Mohr-Coulomb准则的具体表达式为

(19)

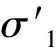
2.2 强度参数弱化规律

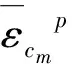
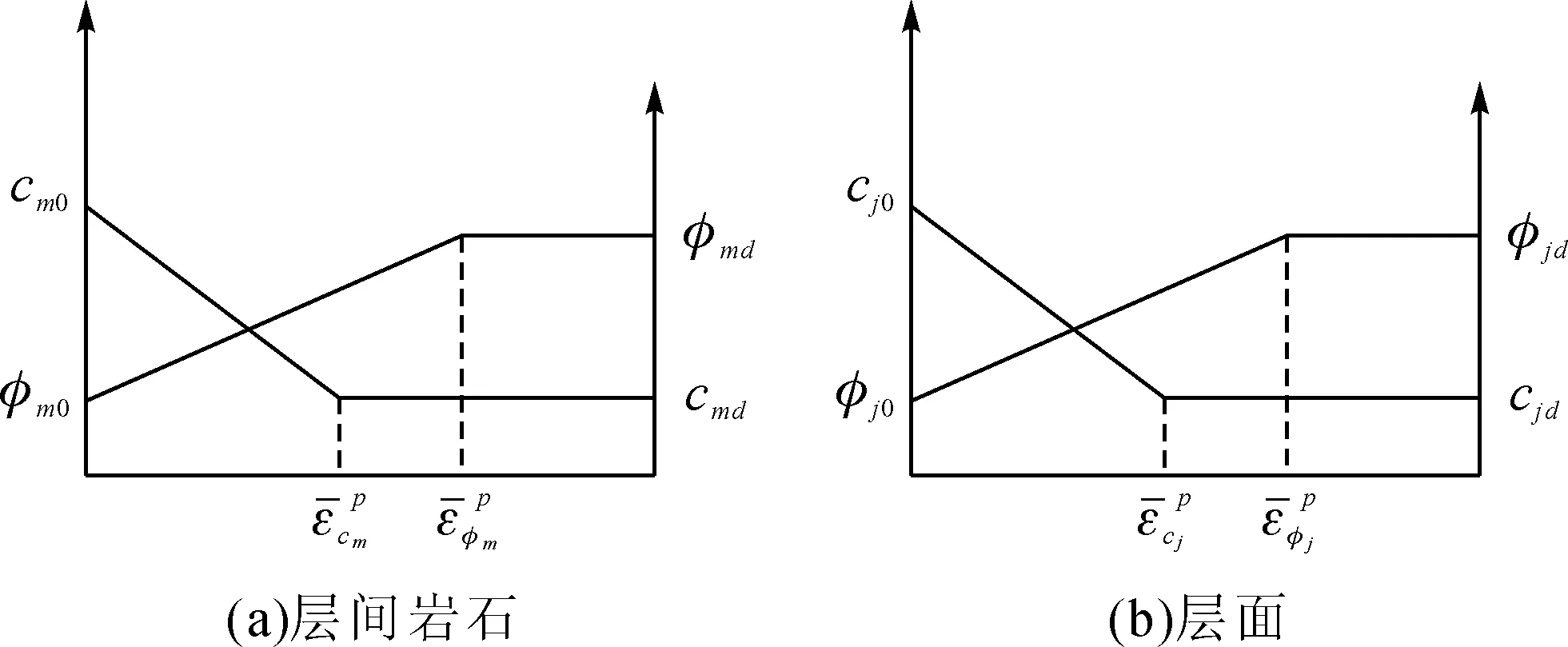
图5 强度参数随等效塑性应变的变化规律图

3 工程应用

3.1 工程背景

乌东德水电站厂区地层主要由褶皱基底浅变质岩及盖层沉积岩构成，褶皱基底左岸分布在高程1 000～1 200 m 以下，右岸分布在高程1 400～1 600 m以下，上部为不整合接触缓倾盖层。褶皱基底地层陡倾、岩层走向与河流走向大角度相交，岩性主要为中厚层～厚层变质灰岩、大理岩和白云岩，地下厂房围岩稳定总体条件优良。空间地应力测试成果表明，左岸厂房开挖区岩体内第一主应力皆属中等地应力水平，量值较集中，范围为11.3～14.9 MPa，平均值为13.3 MPa，方位多集中在40°～70°和210°～270°；倾角较多集中在30°～60°。右岸厂房开挖区岩体内第一主应力皆属低～中等地应力水平，范围为5.6～13.0 MPa、平均值为7.2 MPa；方位角相对较多集中在290°～340°和120°～180°；倾角较多集中在30°～80°。水电站地下厂房洞室群区域层状岩体分布广泛，具有工程规模大、洞室布置密集、挖空率较高等特点，因此在洞室群的施工建设中遭遇较为突出的大跨度、高边墙洞室稳定问题。

3.2 分析与验证

图6为根据实际地质勘查资料和施工开挖组织设计建立的乌东德左右岸地下厂房围岩稳定分析模型。模型在设定初始地应力场时以自重应力为主，并考虑了地表剥蚀的影响(图6a)，同时为降低模型的总体网格数量在厂房开挖周边一定范围内网格进行了精细剖分(图6c、d)，其他区域则粗分。图6中，Pt2l2-2为互层灰岩夹大理岩化白云岩；Pt2l2-3为互层夹中厚层、薄层的大理岩化白云岩；Pt2l3-1为厚层-巨厚层灰岩；Pt2l3-2为巨厚层白云岩夹薄层灰岩；Pt2l3-3为厚层夹中厚层灰岩；Pt2l3-4为厚层白云岩夹中厚层石英岩；Pt2l3-5为中厚层夹薄层灰岩；Pt2l4-1为极薄层-薄层大理岩化白云岩。

图6 乌东德地下厂房围岩稳定分析模型图

地应力根据文献[7]的地应力测试结论，采用自重应力场。力学模型采用本文提出的横观各向同性劣化模型，其力学参数采用文献[8]提供的反演参数。为验证计算结果合理性，将计算获得的松动圈与现场实测松动圈结果进行对比。数值计算中的围岩松动圈主要以Xu等[9]等提出的基于该模型的层状岩体破坏接近度指标FAI来划定，该指标认定在大于1.0时岩体屈服；对于围岩开始松动所对应的FAI值需根据现场实测信息和工程经验予以确定。这里以1.05作为围岩开始松动所对应的FAI值。

图7为典型机组断面(1、3、5、7、10号和12号机组断面)在第Ⅴ层开挖后松动圈分布云图。从图7中可以看出围岩松动圈的大小与洞室开挖尺寸密切相关，洞室尺寸越大，松动圈相对而言更大。不过，总体而言，围岩松动圈深度不大，在0～3.5 m之间。图8为乌东德水电站左、右岸地下厂房Ⅴ层开挖后各典型剖面围岩松动圈深度的计算结果与监测结果对比。从图8中可以看出，地下厂房各监测点测试获得松动圈深度与计算获得的松动圈深度比较接近。这表明采用层状岩体的横观各向同性弹塑性耦合模型并结合与之配套的层状岩体破坏接近度指标，预测层状岩体洞室的围岩松动圈分布特征是可行的。

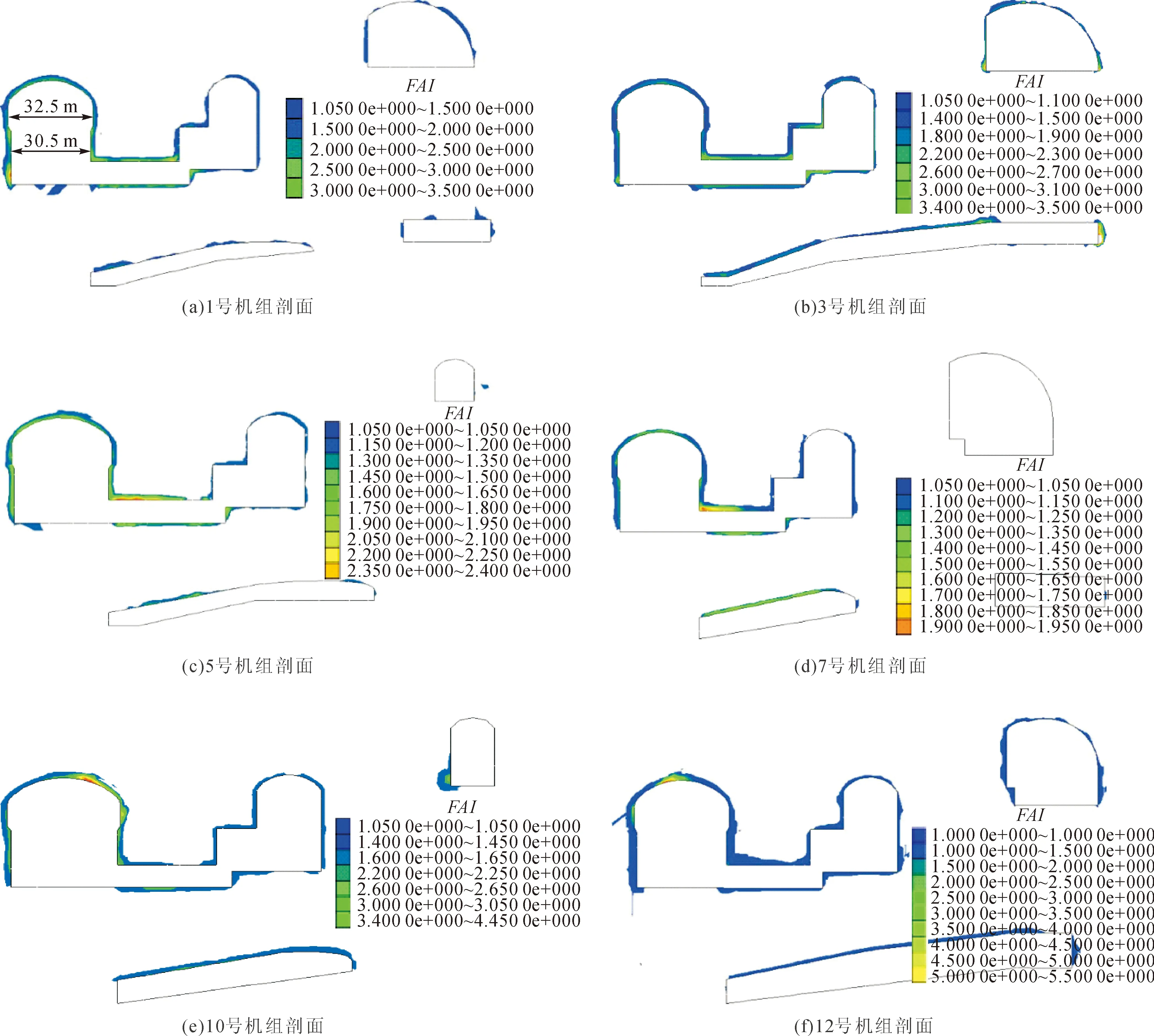
图7 典型机组剖面第V层开挖后松动圈分布云图

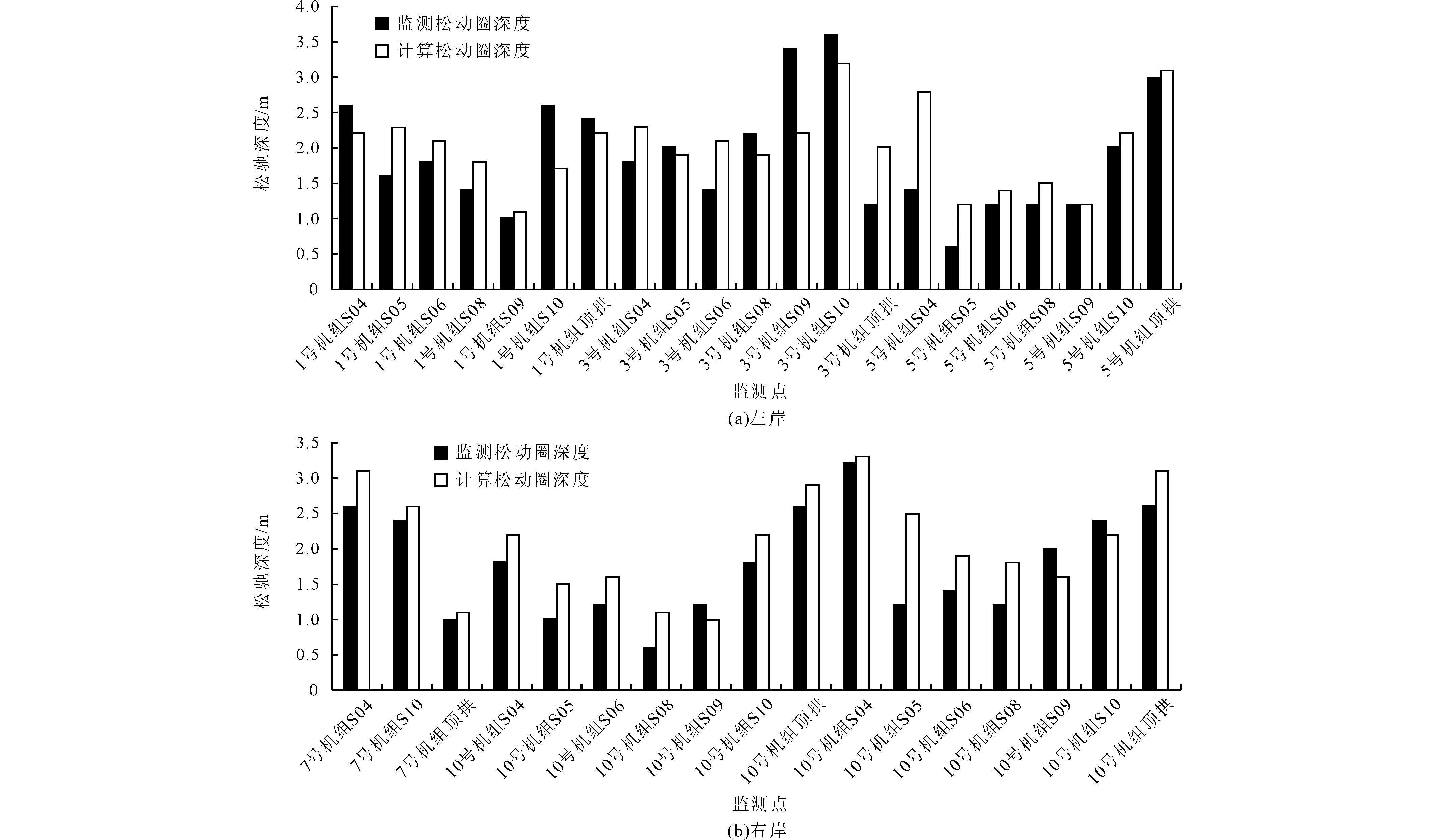
图8 主厂房典型机组剖面监测点处第Ⅴ层开挖后监测松动圈深度与计算松动圈深度对比图

4 结 语

将层状岩体视作层间岩石与层面组成的复合材料，分别就层间岩石和层面的力学性质建立相应的力学模型，并考虑横观各向同性条件下强度参数弱化和弹性参数劣化规律，最终建立了一个可描述层状岩体力学特性的横观各向同性弹塑性耦合模型.将该模型应用于乌东德水电站陡倾层状岩体洞室的围岩开挖稳定性分析，并与现场监测结果进行了对比分析，证明了该模型的工程适用性，最终得到如下结论：

1)层状岩体的横观各向弹塑性耦合模型抓住了层状岩体破坏的实质，即层状岩体的破坏由当前状态下的层间岩石或层面的破坏引起，因而可有效表征层状岩体在开挖扰动下的破坏模式；

2)层状岩体的横观各向弹塑性耦合模型既可以考虑层状岩体强度在峰后随塑性应变增大而减小的情况，也能描述其弹性模量在峰后随塑性应变增大而不断劣化的现象，可为更准确地模拟层状岩体洞室开挖的力学响应提供了理论模型支撑；

3)基于层状岩体的横观各向同性弹塑性耦合模型和破坏接近度指标的乌东德地下厂房围岩稳定分析结果显示，地下厂房Ⅴ层开挖后各监测点测试获得松动圈深度与计算获得的松动圈深度比较接近，表明采用层状岩体的横观各向同性弹塑性耦合模型并结合与之配套的层状岩体破坏接近度指标，预测层状岩体洞室的围岩松动圈分布特征是可行的。