环境激励下钢板组合梁桥模态参数识别

李超，王佐才、2，李德安

（1.合肥工业大学土木与水利工程学院，安徽 合肥 230000；2.土木工程防灾减灾安徽省工程技术研究中心，安徽 合肥 230000）

1 引言

随着土木工程技术的快速发展，桥梁建设事业取得了长足的进步，但随之而来的桥梁的安全状况问题更加突出。在已建成和正在修建的桥梁工程中，急需采用切实有效的检测手段进行安全评估，识别和控制损伤，防止灾难发生。结构一旦发生损伤，必然引起其物理特性的变化，即结构模态参数的变化。一般情况下结构模态参数包括以下3个方面，即结构的阻尼比、结构的振动频率以及结构各阶模态的振型。此外，利用模态参数对桥梁结构进行损伤识别和安全评估具有十分重要的工程意义。

传统的模态参数识别方法需要同时测得激励和响应信号，但是在一些大型结构中无法施加激励或者施加激励成本很高，因此对结构在环境激励下的模态参数识别尤为重要。环境激励下桥梁结构的模态参数识别具有以下优点：①只需要根据结构在环境激励下的响应信号就可以识别结构的模态参数，而且识别的结果能真实的反映结构的动力学特性；②无需额外施加激励，不会对结构造成损伤。

本文以一座四跨连续钢板组合梁桥为研究背景，利用设计院提供的结构设计图纸建立了该桥梁的FEM模型，并通过环境激励试验测得结构的加速度响应，随后利用SSI方法对加速度数据进行分析进一步得到桥梁结构的模态参数，接着提出了在SSI方法的基础上，先利用离散解析模式分解将加速度动态响应分解为模态响应，再利用分解后的模态响应识别结构的模态参数，最后分别对比两种识别结果和有限元分析结果，验证了以上两种方法的适用性，并从中可以发现，在加速度响应时程较短的工况条件下，基于离散解析模式分解方法可以显著提高桥梁结构阻尼比识别的准确性。通过利用这两种方法对环境激励下的桥梁结构进行模态参数识别，可以深入了解桥梁动力特性，并且可以利用测试结果修正有限元模型，对于桥梁结构更好的维护和使用具有重要的意义。

2 基于环境激励的模态参数识别理论

2.1 随机子空间法

随机子空间法（SSI）是一种典型的环境激励下结构模态参数识别方法，系统的空间模型描述如下：

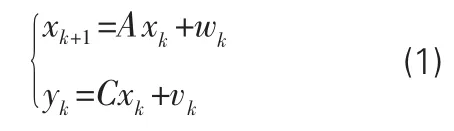
式中：xk为离散的时间状态向量；yk为输出向量；vk是传感器误差引起的噪声，wk是处理过程和建模误差引起的噪声；矩阵A为离散状态矩阵，矩阵C为离散输出矩阵。假设wk与vk是均值为零的高斯白噪声，同时，wk和vk的协方差矩阵Q、S、R满足下式：

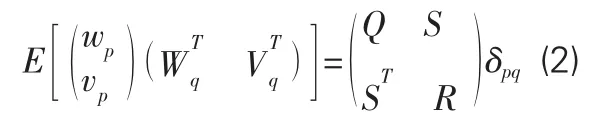
式中E为数学期望，δpq表示克罗内克算子（当 p=q时,δpq=1，当 p=q时,δpq=0），p和q是任意两个时间点。

基于SSI的参数识别方法首先需要将系统输出响应组成系统的分块Hankel矩阵，接着对分块Hankel矩阵的行进行投影得到行投影矩阵，最后利用SVD进行矩阵分解，经过一系列变换得到离散状态矩阵A和输出矩阵C，利用现有方法即可以得到结构的模态参数。

系统的离散状态矩阵A可表示为：

式中：Λ＝diag（λ）i（i=1,2，…，n）；Ψ为系统的特征向量矩阵。

根据离散时间系统和连续时间系统的特征值关系，求出连续时间系统的特征值和特征向量：

式中：λi为离散时间系统的特征值，为连续时间系统的特征值。再根据模型特征值与系统的模态阻尼比ξ、固有频率ω的关系：

得到系统的固有频率和阻尼比。

系统的振型可由输出矩阵C和特征向量矩阵Ψ得到：

2.2 基于离散解析模式分解的模态参数识别方法

2.2.1 解析模式分解

解析模式分解（AMD）是信号处理方法的一种，其主要目的是用来提取某段频率范围内的信号数据，一般情况下，对于实测试验数据可利用AMD提取所关心的信号数据。AMD定理的相关描述如下：

假设原信号是x（t）由多个频率的子信号组成，相应的频率分量为（ω1，ω2，…，ωn）。原信号可被分解为n个子信号此时 x（t）可以被表示为：

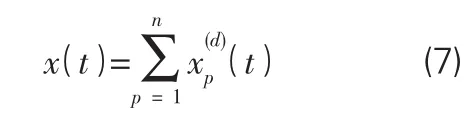
如果x（t）中的每一个频率分量满足：ω1＜ωc1，ωc1＜ ω2＜ωc2…，ω（cn-1）＜ωn＜ωcn其中ωcp为选定的截断频率，则每个子信号分量可以表示为：

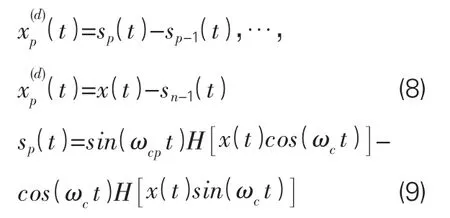
式中，表示对括号中的函数进行希尔伯特变换。理论的核心是利用选取的截止频率提取结构振动响应信号中的低频部分，且能够由下式获得：

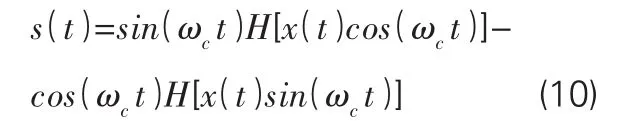
因此，上式如同一个低通滤波器，滤掉了信号的高频部分，通过了信号的低频部分。

2.2.2 离散解析模式分解

由于解析模式分解方法是对于连续信号的推导，当信号为离散信号时，可能会导致低频部分提取失败。因此，为了能够有效分析离散信号，在解析模式分解的基础上进一步提出了离散解析模式分解（DAMD），DAMD定理描述如下：

对于一个具有N个样本点的离散信号：x（1），x（2），…，x（i），…（i=0，1，2，…，N-1），离散信号的各个分量可以表示为：

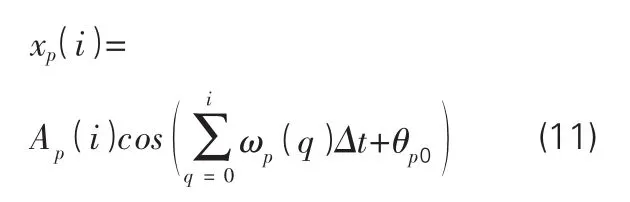
式中ωp（q）表示信号分量xp在时间点 qΔt处的频率，θp0为信号分量 xp的初始相位角。则式(10)的离散形式可以表示为：

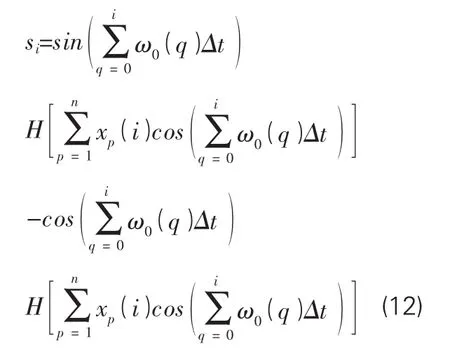
如果在任意时间点qΔt处，都有ωp（q）≤ωs/4，则频率满足，

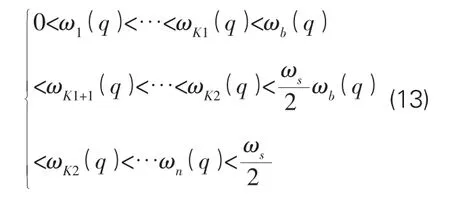
式中，ωs是离散时间序列的采样频率。ωK（1q）代表采样频率的第K1个分量，ωK（2q）代表采样频率的第K2个分量。

因此，解析模式分解的离散形式可以进一步表示为：

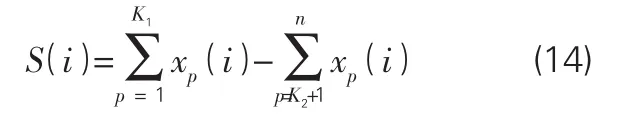
在上式中，对于解析模式分解的离散形式，分解信号S（i）包括低频分量和高频分量，为了消除高频成分，进一步提出了两步式AMD，并命名为DAMD，其步骤如下：

第一步：输入信号 x（i）/2，选取合适的截止频率，滤出信号S（'t）。

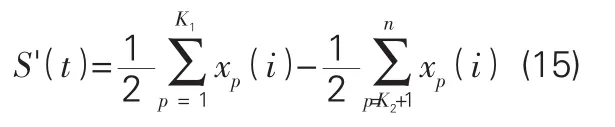
第二步：将第一步滤出的信号S（'t）作为输入信号，选择与第一步相同的截止频率，滤出信号S（"t）。

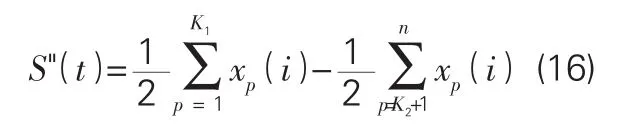
通过叠加上面两个公式，可以发现提取的低频信号的频率在任意时间点均小于截止频率。

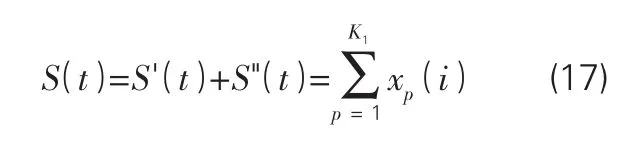
3 数值模拟

该连续钢板组合梁桥跨径为（4×35）m，主梁采用双工字钢板组合梁，组合梁桥面全宽26.5m，钢梁中心线处的梁高为1.75m。主梁标准横断面如图1所示。

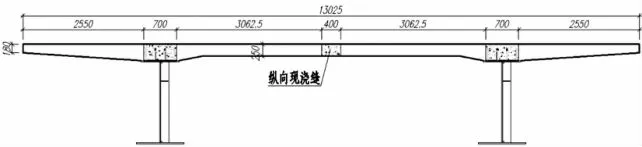
图1 主梁横断面图（mm）

根据设计图纸提供的截面尺寸，材料参数以及边界条件，以SAP2000有限元软件为平台，建立该钢板组合梁桥的有限元模型，桥梁有限元模型如图2所示。

图2 基于SAP2000建立的空间有限元模型

利用该软件建立的空间有限元模型，进行模态分析,得到模型的前两阶频率和振型，如图 3（a）和（b）所示。

诸多材料记载，镜湖处士方干早年热衷于谋求功名。据《唐才子传》：“干早岁偕计，往来两京，公卿好事者争延纳。”[6]375但方干天生丑陋的相貌使他几乎断绝了仕进的希望。《鉴戒录》记载：“有司议干，才则才矣，不可与缺唇人科名，四夷所闻，为中原鲜士矣。”[7]卷八在归隐镜湖后，方干并没有放弃博取功名的努力。正因为镜湖处于浙东政治中心越州，他希望通过干谒当时的权贵以获得仕进的机会，并且为此补好了自己的缺唇，然而时运不济终究没有获得仕进的机会。

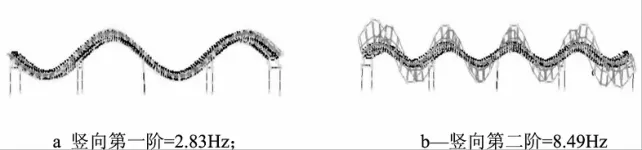
图3 桥梁模型前两阶竖向振型

4 环境振动试验

通车前为了全面了解该桥的固有动力特性，对其进行了环境激励下的振动试验，主要测试在车辆激励下桥梁结构的振动加速度响应。

为了能够测得全桥纵向前若干阶的频率和振型，沿桥跨纵向共布置了15个测点，每个测点都布置了纵向加速度传感器，测点平面布置图如图4所示。

图4 桥面测点布置图

运用加速度采集系统选择在正常时段进行加速度数据采集，由传感器拾得环境激励下桥跨结构振动加速度信号,采样频率100Hz，其中C6测点的加速度时程响应如图5所示。

为了研究前文两种方法识别结构模态参数的准确性，本文一共考虑了四种工况。工况一：使用SSI方法直接分解时长20s的加速度响应信号，识别结构的模态参数。工况二：使用SSI方法直接分解时长100s的加速度响应信号，识别结构的模态参数。工况三：基于离散解析模式分解方法，采用20s的加速度响应时程，识别结构的模态参数。工况四：基于离散解析模式分解方法，采用100s的加速度响应时程，识别结构的模态参数。

模态参数识别结果

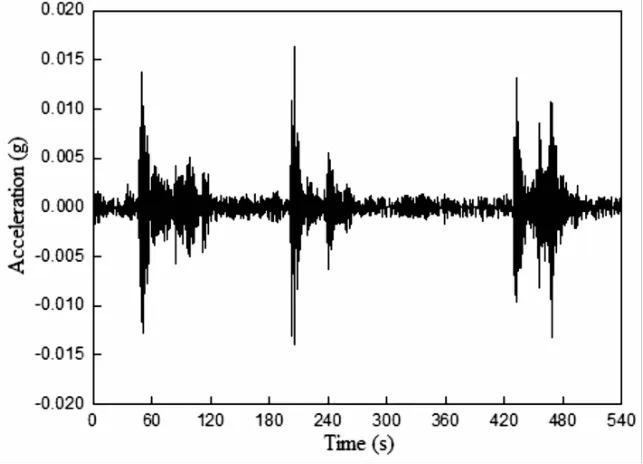
图5 C6点加速度时程响应

工况二中，对传感器采集到的加速度信号经过滤波，降噪处理后，采用随机子空间法对其直接进行参数识别，得到桥梁结构基于SSI方法在竖向振动下的频率稳定图，如图6所示，在信号稳定图中选取稳定点，并使所选取的稳定点的阻尼比小于5%，得出的梁桥的一阶竖弯频率为 2.67Hz，二阶竖弯频率为8.04Hz。工况四中，利用离散解析模式分解，可以有效的将动态响应分解为模态响应，得到的结果如图7所示，通过识别分解后的模态响应，得到梁桥的一阶竖弯频率为 2.64Hz，二阶竖弯频率为8.05Hz。工况一和工况三的识别步骤分别同工况二和工况四。

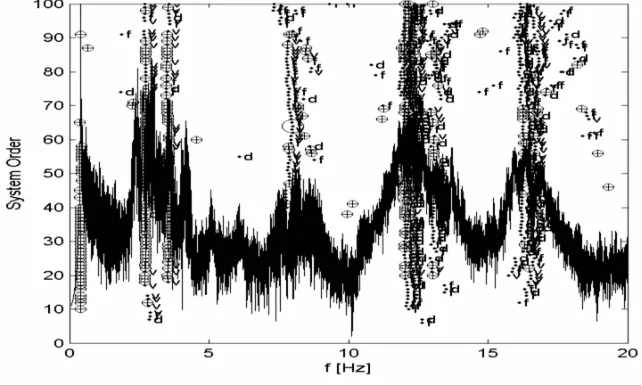
图6 基于SSI竖向振动频率稳定图

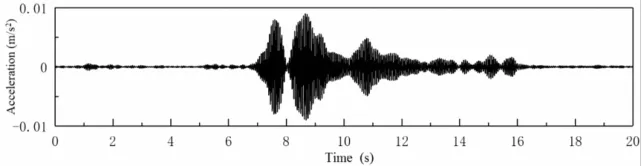
图7 模态响应图

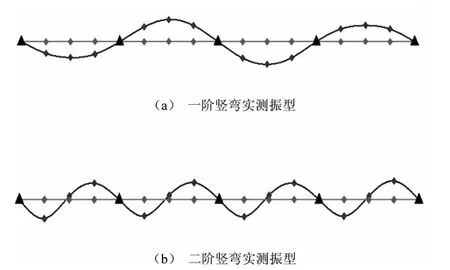
图8 结构振型图

四种工况下桥梁固有频率和阻尼比的识别结果如下表所示。

以工况二为例，其相应的振型图如图 8（a）和（b）所示。

将基于DAMD方法识别的桥梁固有频率同直接使用SSI法和有限元计算结果对比，可以发现，四种工况下所确定的桥梁固有频率基本一致。但是，工况一中识别的结构阻尼比与其他三个工况识别结果相比差别较大，也就是说，通过SSI方法确定的结构阻尼比与加速度响应时程的长度有关，时间历程短会导致阻尼比的识别结果出现较大误差，与工况四的识别结果相比，SSI方法识别的阻尼比最大误差为50%。同时，基于DAMD方法所确定的结构阻尼比，在加速度响应时程较短的工况下，其识别的结果仍具有较高的精度。

根据工况二得出的一阶与二阶竖弯振型结果，和前文中基于有限元软件得到的一阶和二阶振型图比较，发现形状吻合，这说明利用SAP2000有限元软件推导梁桥的振型以及频率都是真实可行的，也说明了利用基于DAMD方法可以有效的将结构的动态响应分解为模态响应，分解后的模态响应可进一步用于模态参数识别，结果表明该方法能够较好的识别梁桥的工作模态参数。

5 结语

本文研究了基于环境激励下钢板组合梁桥的模态参数识别方法，分别采用了随机子空间法和基于离散解析模式分解方法对桥梁结构的模态参数进行识别，将识别的结果同理论值进行对比，得到以下结论：

①SSI法和基于DAMD方法识别出的桥梁结构的固有频率和理论值误差结果较小，表明两种方法对该钢板组合梁桥固有频率的识别效果良好；

②基于DAMD方法对桥梁结构阻尼比的识别精度高于SSI法，特别是在加速度响应时程较短的工况下，利用DAMD方法可以显著提高桥梁结构阻尼比识别的准确性。