基于改进三参数灰色模型的海上交通事故预测

徐东星， 尹 勇， 张秀凤， 孙 珽， 叶 进， 付昭斌

(1.广东海洋大学 海运学院， 广东 湛江 524088; 2.大连海事大学 a.航海学院;b.航海动态仿真和控制交通行业重点实验室， 辽宁 大连 116026)

海上船舶交通事故(包括碰撞、搁浅、触礁、触损、浪损、火灾/爆炸、自沉和其他)的预测和控制是海上交通管理的重要内容，其预测的准确性将直接影响海上通航能力和海洋环境，关系到海上航行安全。目前，国内外水上交通事故常用的预测方法有时间序列预测模型、自回归预测模型、神经网络模型、支持向量机和马尔科夫模型等。[1-2]受诸多因素的影响，水上交通事故的发生具有随机性和不确定性，而灰色预测模型对解决 “部分信息已知、部分信息未知”的海上船舶交通事故预测具有很好的适用性。

目前,学者们利用不同的灰色系统方法对不同海域的海上船舶交通事故进行预测和分析，不同的灰色理论方法预测水上交通事故的结果与实际情况会存在不同程度的差异。郝庆龙等[3]和牛佳伟等[4]分别采用加权灰色关联理论、改进关联系数的加权灰色关联理论和加权灰色预测模型对宁波水域和辽宁水域的海上交通事故的主要致因和事故数量进行分析和预测,取得满意结果，但是加权灰色预测模型在确定模型参数时需要人为选取合适的权值矩阵。甘浪雄等[5]采用摆动灰色模型对某港口的海上交通事故进行定量计算，并结合定性分析来预测未来该港口海上交通事故数量和事故种类的比例,该模型对摆动幅度较大的原始数据具有较好的预测精度。陈海山等[6]对海上交通事故数呈现非单调的摆动发展趋势的序列采用灰色Verhulst模型对其预测，拟合效果良好。王祺等[7]采用马尔科夫链对系统云灰色模型的海上交通事故预测值进行修正，并采用等维递补法和滑动转移概率法对组合模型进行改进，结果令人满意。李铃铃等[8]基于误差补偿思想，采用BP(Back Propagation)神经网络对灰色预测模型进行残差修正，建立灰色神经网络模型对海上交通事故进行预测。王当利等[9]引入诱导有序加权平均(Induced Ordered Weighted Averaging,IOWA)算子对灰色模型和支持向量机的回归模型进行组合，对全国和长江某流域的水上交通事故进行预测。陈昌源等[10]通过引入弱化缓冲算子降低原始数据的随机性对传统的灰色预测模型进行改进，对我国海上交通事故进行预测并取得良好的效果。但文献[7]～文献[10]所采用的海上交通事故灰色预测模型仅对数据进行预处理或基于误差补偿思想对预测结果进行残差修正等措施来提高模拟精度和预测精度，忽略灰色预测模型结构固有的局限性。因此，本文针对基于非齐次指数离散函数的灰色模型NHGM(1,1,k)在海上交通事故预测中存在的不足，提出一种优化背景值和残差综合修正的三参数灰色预测模型INHGM(1,1,λ,k)，通过改进的自适应粒子群优化(Adaptive Particle Swarm Optimization,APSO)算法对模型中的初始值和背景值进行优化计算，并用优化模型对我国海上交通事故数进行模拟和预测。结果表明：改进的INHGM(1,1,λ,k)模型模拟和预测的平均相对误差比NHGM(1,1,k)模型更小，并且预测精度较传统GM(1,1)模型有所提高，减少原模型的由于参数近似替代所导致的模拟误差，为海上交通事故预测提供新的理论基础和方法。

1 灰色预测模型NHGM(1,1,k)基本原理

设非负序列X(0)=(x(0)(0),x(0)(1),…,x(0)(n))为原始序列，X(1)=(x(1)(0),x(1)(1),…,x(1)(n))为X(0)的一阶累加序列，[11-12]Z(1)为X(1)紧邻均值生成序列，有

(1)

式(1)为NHGM(1,1,k)的基本形式(以下简称三参数灰色预测模型)。将一阶微分方程求导为

(2)

式(2)为三参数灰色预测模型NHGM(1,1,k)的白化微分方程。

(3)

则NHGM(1,1,k)模型为

(4)

最小二乘参数估计需满足：

(5)

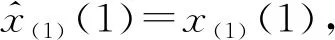
(6)

还原值为

k=1,2,…,n-1

(7)

3) 在三参数灰色预测模型模拟误差平方和最小的前提下，模型的最优初始条件为

(8)

2 改进三参数灰色模型的构造

2.1 NHGM(1,1,k)模型的背景值重构

在系统学习NHGM(1,1,k)模型建模机理的基础上，发现影响模型的模拟和预测精度与背景值的构造形式有关。当原始序列波动较大时，背景值的构造采用紧邻均值生成的形式为

z(1)(k)=0.5[x(1)(k)+x(1)(k-1)]

(9)

式(9)会引起较大的滞后误差，存在一定的缺陷。为此，引入一种背景值优化方法为

z(1)(k)=λx(1)(k)+(1-λ)x(1)(k-1)

(10)

式(10)中：0≤λ≤1。

设:

(11)

(12)

根据灰色建模理论可知:式(11)与式(12)需同时成立，联立式(10)、式(11)与式(12)可得

(13)

在式(10)中，如果λ仅取值0.5，会导致模拟与预测精度变差。对背景值重构的灰色模型简称为NHGM(1,1,λ,k)。

2.2 残差修正的NHGM(1,1,λ,k)参数综合优化模型

根据灰色系统理论建模的思想可知:对原始序列进行平移和残差修正可提高灰色模型的模拟与预测精度。[13-14]在综合考虑优化初始值与背景值的基础上，首先对原始序列进行平移变换，再建立NHGM(1,1,λ,k)模型；根据灰色模型的预测值与原始序列求取残差序列，然后对残差序列建立NHGM(1,1,λ,k)模型；对灰色模型的模拟值进行残差修正即可得到校正后的预测值。具体建模步骤如下：

设原始序列为

X(0)={x(0)(k)},k=1,2,…,n

(14)

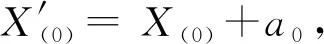
3) 模型预测值为

(15)

4) 残差序列为

(16)

5) 对残差序列进行平移变换得到新残差序列(a1为平移量)为

(17)

7) 对NHGM(1,1,λ,k)模型进行残差修正的预测值为

(18)

实际使用过程需要对以上模型中的未知参数(平移值、背景值系数、初始值修正量)进行计算。采用改进的APSO算法，以均方根误差(Root-Mean-Square Error, RMSE)最小为约束条件，进行函数寻优计算，得到最优的模型参数值。对背景值进行优化和残差综合修正的模型称为改进的三参数灰色模型(简称INHGM(1,1,λ,k))。

3 改进的自适应粒子群算法优化灰色模型

3.1 自适应粒子群算法

KENNEDY等[15]提出一种群体智能寻优算法即粒子群优化(Particle Swarm Optimization，PSO)算法。该算法的基本思想如下：

1) 假设在一个D维的搜索空间中，由n个粒子组成的种群X=(X1,X2,…,Xn),其中第i个粒子表示为一个D维的向量Xi=(xi1,xi2,…,xiD)T,代表第i个粒子在D维搜索空间中的位置，即问题的潜在解。

2) 根据适应度函数即可计算出每个粒子位置Xi对应的适应度值。第i个粒子的速度为vi=(vi1,vi2,…,viD)T,其个体极值为Pi=(Pi1,Pi2,…,PiD)T,种群的群体极值为Pg=(Pg1,Pg2,…,PgD)T。

3) 粒子通过个体极值和群体极值更新自身的速度和位置，直到达到终止条件时停止搜索，即

(19)

(20)

式(19)和式(20)中：w为惯性权重；d=1,2,…,D；i=1,2,…，n；k为当前迭代次数；vid为粒子速度；c1和c2为自适应学习因子，属于非负的常数；r1和r2属于[0,1]的随机数。

为提高粒子群算法的寻优能力，避免在寻优过程中出现早熟收敛现象，引入自适应调整惯性权重和学习因子的APSO。自适应惯性权重为

(21)

自适应学习因子[16]为

(22)

式(21)和式(22)中：k为当前迭代次数；Iter为最大迭代次数；wstart为惯性权重初始值；wend为最终惯性权重。通常取wstart=0.9，wend=0.4。

3.2 自适应粒子群算法优化灰色预测模型参数的算法步骤

采用改进的APSO算法对INHGM(1,1,λ,k)模型的参数(平移值、背景值、初始值修正量)进行寻优，以RMSE为适应度函数，得到最优的模型参数值。具体优化步骤如下：

1) 参数初始化即随机初始化粒子的位置和速度，粒子维数为6维：

Pi=(a0i,λ1i,η1i,a1i,λ2i,η2i)

Vi=(vi1,vi2,vi3,vi4,vi5,vi6)

(23)

式(23)中：0≤λ1i,λ2i≤1。

2) 以RMSE为目标函数计算粒子的适应度值(目标函数值)，再根据目标函数值确定个体和群体极值。目标函数为

(24)

3) 根据粒子位置和速度更新公式，对粒子速度和位置进行更新，计算粒子的适应度值，并与个体和群体极值进行比较，取粒子的适应度值、个体极值与群体极值中的较小者为当前粒子的位置。

4) 当粒子的适应度值达到预设的精度或迭代次数超过预设的迭代次数即停止搜索，输出全局最优模型参数即粒子的最优位置。

4 实例试验与分析

以2004—2018年我国海上交通事故数据(摘自《交通运输行业发展统计公报》){562 532 440 420 342 358 331 298 270 262 260 212 196 196 176}(单位:起)为研究样本，分别建立NHGM(1,1,k)模型和本文提出的优化模型INHGM(1,1,λ,k)，验证所提出的灰色预测模型的准确性和预测精度。

1) 选取2004—2012年的部分历史数据为建模样本，然后对2013—2014年我国海上船舶交通事故进行预测并与文献[10]预测结果相比较，验证模型的准确性。在MATLAB语言环境下分别建立NHGM(1,1,k)模型和本文提出的优化模型INHGM(1,1,λ,k), 其中:APSO的粒子总数为80;最大迭代次数为200。两种模型的模拟值和预测值及其相对误差，见表1～表4。

表3 NHGM(1,1, k)模型预测值

表4 INHGM(1,1,λ,k)模型预测值

由表1和表2可知：基于INHGM(1,1,λ,k)模型的平均相对误差3.172 2%比原始NHGM(1,1,k)模型的平均相对误差4.076 6%小0.905 4%。为验证改进模型的预测精度，分别对2013—2014年的我国海上船舶交通事故进行预测。原始NHGM(1,1,k)模型预测值分别为2013年286起、2014年277起,如表3所示。INHGM(1,1,λ,k)模型预测值分别为2013年268起、2014年258起,如表4所示。2013年与2014年实际海上交通事故分别为262起、260起，结果表明:本文提出的INHGM(1,1,λ,k)模型比NHGM(1,1,k)模型的预测精度高，预测精度为0.76%～2.29%，与文献[10]预测结果相近，可为海上交通事故预测与控制提供新的理论依据。

2) 为比较优化模型与其他灰色模型的预测精度，选取2004—2016年的部分历史数据为建模样本，然后对2017—2018年我国海上船舶交通事故进行预测并与NHGM(1,1,k)模型、传统GM(1,1)模型预测结果进行比较，见表5～表8。由表5～表8可知：本文提出的模型的模拟精度优于原始NHGM(1,1,k)模型，低于传统GM(1,1)模型，但优化模型的预测精度高于GM(1,1)模型与NHGM(1,1,k)模型。本文采用优化模型对2019年我国水上交通事故进行预测，预测值为176起。从预测结果来看，我国水上交通事故趋势平稳。

表5 GM(1,1)模型模拟值

表6 NHGM(1,1, k)模型模拟值

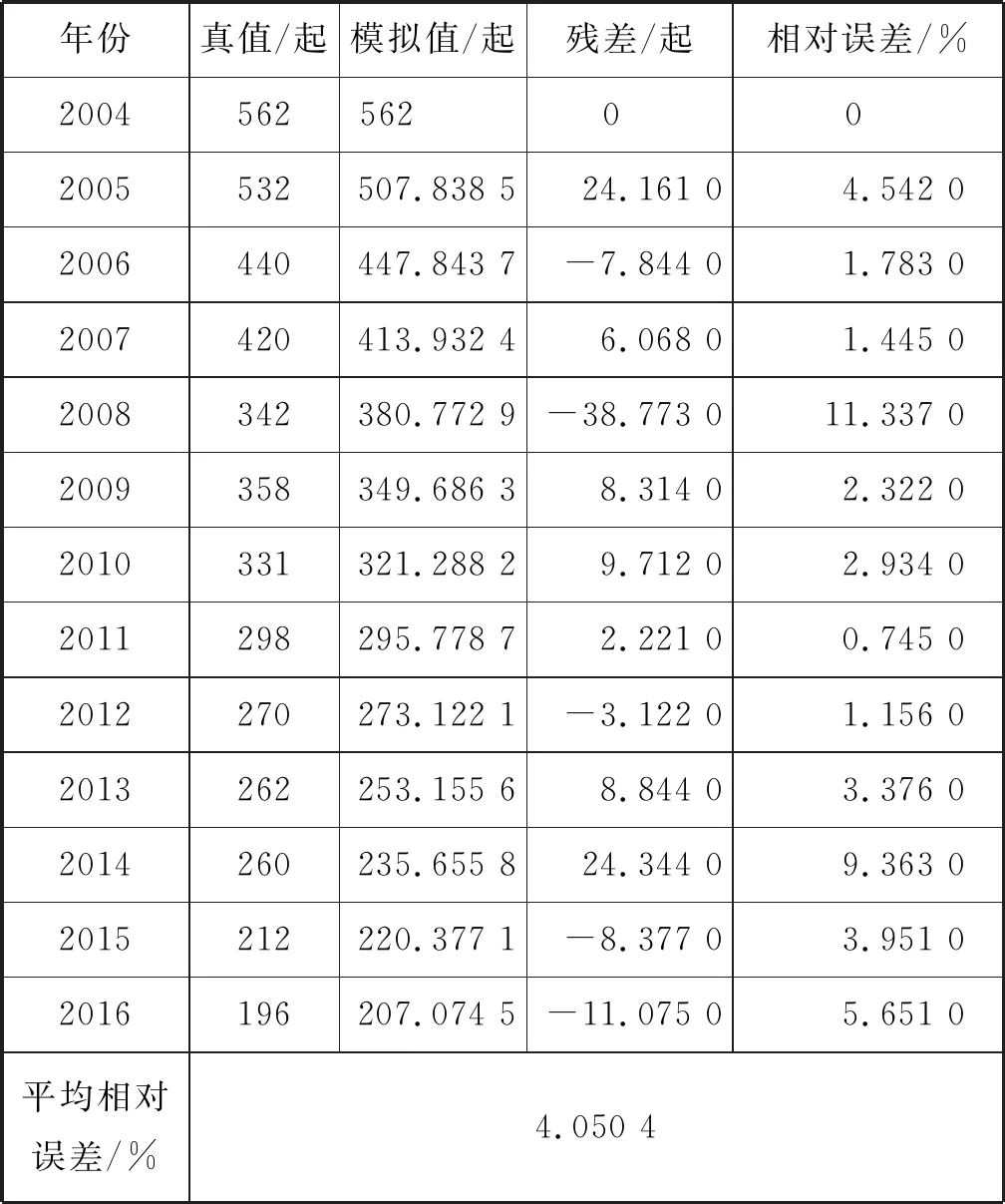
表7 INHGM(1,1,λ, k)模型模拟值

表8 模型预测值比较 起

3) 为验证优化模型在长期预测中的预测精度问题，选取2004—2011年的部分历史数据为建模样本，对2018年我国海上船舶交通事故进行预测。优化模型预测结果为273起 ，而实际值为176起，相差97起。综上可知：本文提出的模型对海上交通事故短期预测具有较高的预测精度，长期预测的可信度较低。

5 结束语

针对基于非齐次指数离散函数的三参数灰色预测模NHGM(1,1,k)模型存在的不足，提出一种优化背景值和残差综合修正的INHGM(1,1,λ,k)模型，并通过改进的APSO对参数进行优化。通过对2004—2018年我国海上船舶交通事故的模拟值与预测值的分析，可得出以下结论：

1) 改进灰色模型适用于海上交通事故的短期预测，长期预测精度较低。

2) 改进灰色模型与原模型的模拟与预测精度相比较好，并且预测精度高于传统的灰色GM(1,1)模型，在误差允许的范围内，能够较好地反映水上交通事故的发展趋势，具有一定的拟合度和外推性。