管道流模型参数敏感性分析及其在许家沟泉域的应用

武亚遵，李彦涛，林 云，曲鹏冲

(1.河南理工大学资源环境学院，河南 焦作 454000；2.中原经济区煤层(页岩)气河南省协同创新中心，河南 焦作 454000)

我国北方岩溶泉域多为大型的、完整的岩溶地下水系统，系统内地下水贮存和运移较复杂。岩溶介质受岩溶发育程度的影响，多为溶蚀裂隙，少数发育成管道[1-2]。管道的存在使系统内地下水出现偏流，呈现不同流态[3]。在此情况下，若采用多孔介质模型评价系统内地下水的渗流特征，难免会出现一定的误差，甚至与实际完全不符[4]。管道流模型(Conduit Flow Process，CFP)的出现较好地解决了这些问题[5-6]。初期更多的是模型精度的测试和与之有关的研究[7-8]，与实际结合较少[9-10]。近些年来对管道流的研究已从原理、使用方法及适用范围[11]逐渐转向结合实际的应用，比如模拟泉流量对降雨的响应[12-14]、岩溶系统泉流量模拟及溶质离子在系统中的运移等[15-16]，但这些应用多集中在管道发育强烈，部分地段靠落水洞直接补给的南方地区，而将该模型应用于以溶蚀裂隙为主、管道不甚发育，多以含水层间交换补给的北方岩溶地区的研究较少。此外，岩溶管道的特征参数是如何影响系统流量和流态的，尚有待进一步确定。为此，本文拟借助CFP管道流模型探讨管道特征参数对岩溶水系统流量及流态的影响，确定管道各参数的敏感性，而后基于河南鹤壁许家沟泉域水文地质特征构建MODFLOE-CFP模型，对岩溶地下水渗流进行模拟，并预测不同降水保证率下的泉流量，以期为北方大泉保护和地下水开发利用提供借鉴。

1 管道特征的敏感性分析

1.1 管道流模型

为确定岩溶系统管道特征对地下水流的影响程度，构建了一系列CFP管道流模型，并运用离散管道网络与层流结合模型(CFPM1)模拟方式进行求解[2]。模型首先设置了一个5×5×3的空间网格，将含水层分为5行、5列、3层的单元网格，网格的平面大小为10 m×10 m，每层厚3 m。并对含水层基本参数进行设置，包括水平渗透系数为2 m/d，垂向渗透系数为0.2 m/d，贮水系数为0.000 25，模型的初始水头为9 m；模型的第一列为定水头边界，水头值为9 m，其余边界为零通量边界；模型运行50 d，为一个应力期；降雨补给强度为0.003 m/d，并保持不变。岩溶管道在含水层的平面分布见图1。

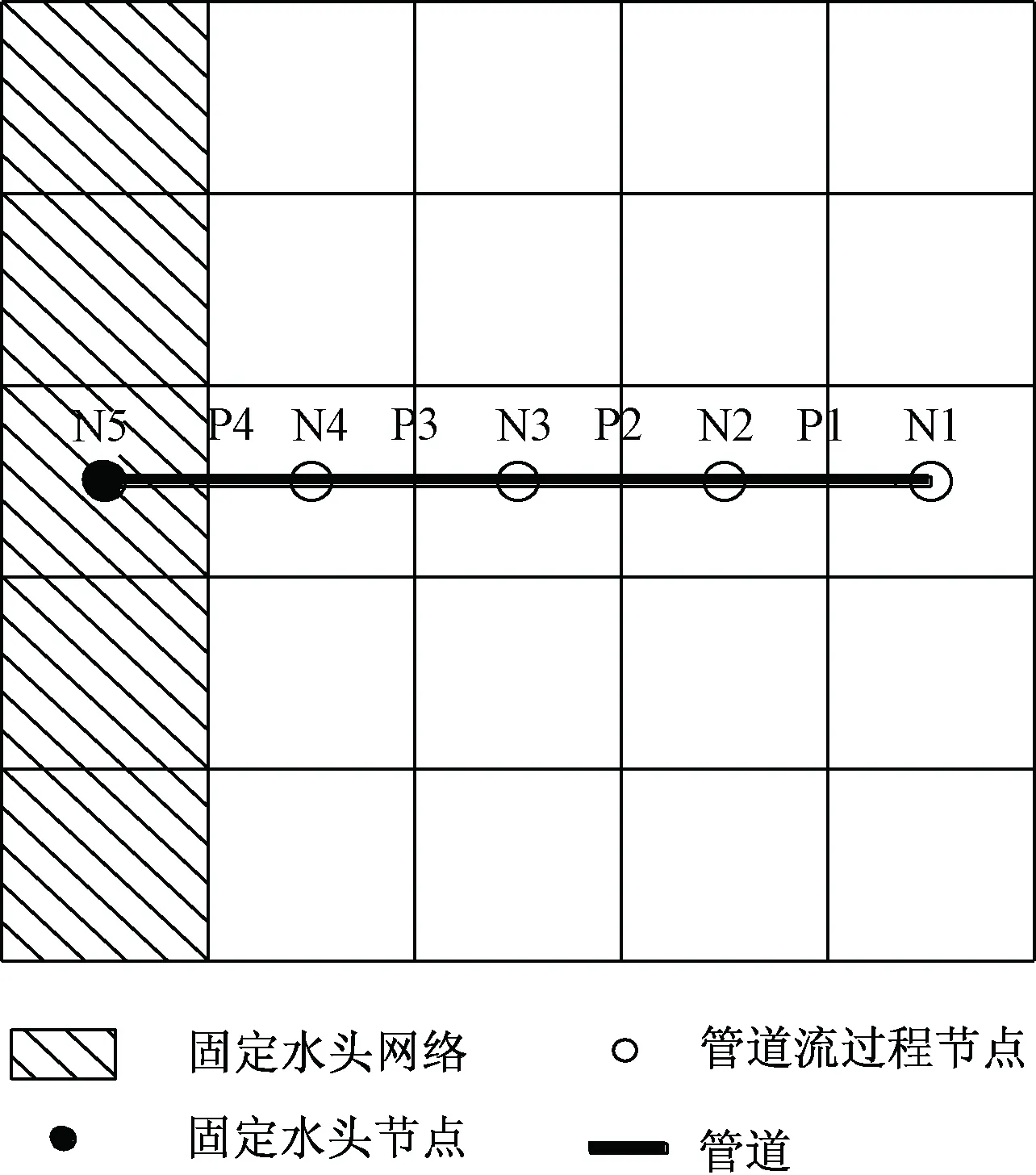
图1 管道分布平面图Fig.1 Pipeline distribution plan

1.2 模拟结果及分析

1.2.1管道特征的影响

(1)管道直径

根据北方泉域勘探资料，岩溶含水层中发育的管道直径多在0.5 m以内，为此探讨了管道直径在0.03～0.50 m范围内的流量和流态变化情况。图2为不同管径下的模拟结果，管径与管道流量呈正相关。当管径小于0.08 m时，流量与管径呈线性关系：Q=3.6d+2.5(R2=0.91)；当管径大于0.1 m时，流量几乎不变。而随着管径的增大雷诺数逐渐减小，管道中水流速度也随之减小。

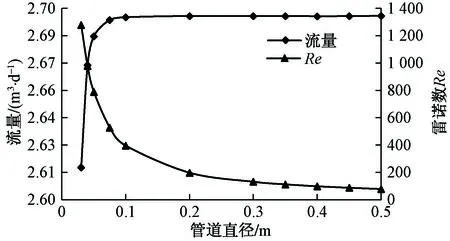
图2 不同管径模拟结果变化曲线Fig.2 Simulation results for different pipe diameters

(2)管道埋深

将整个含水系统分为7层，每次模拟将管道置于一个含水层，保持管径不变，随着管道埋深的增加流量和雷诺数Re先增加后降低(图3)。当管道埋深为2 m时，管道流量达到最大，峰值流量为2.8 m3/d；当流量随埋深增大而降低时，降速逐渐加快，且与埋深呈线性关系：Q=-0.91h+3.5(R2=0.96)。此外在CFP管道流模型中，若管道置于不分层的含水系统或同一含水层不同埋深时，则埋深对流量和雷诺数几乎没有影响。

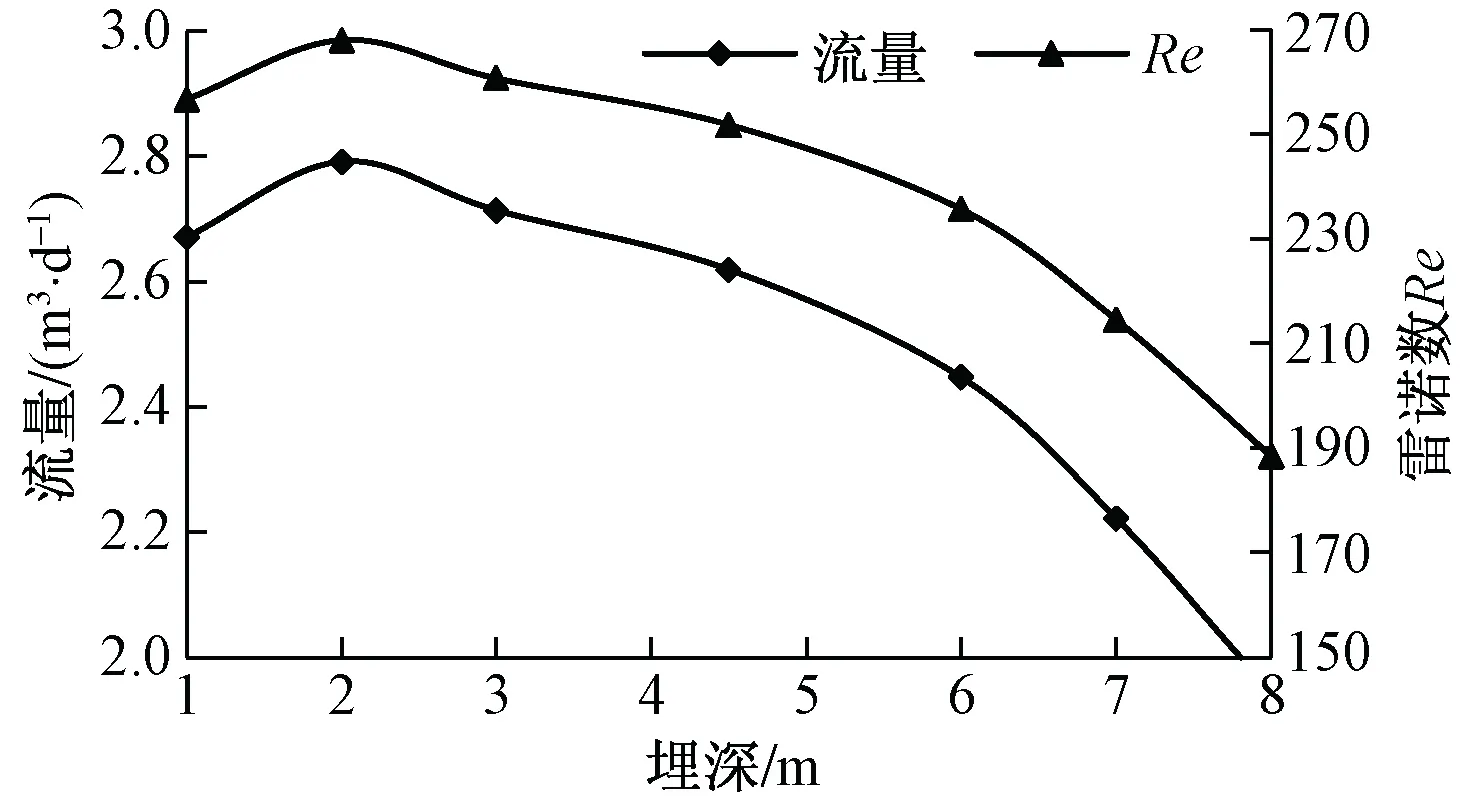
图3 不同管道埋深模拟结果变化曲线Fig.3 Curves of simulation results for different pipeline depths

(3)管道坡度

当管径和埋深保持不变时，管道坡度与管道流量及雷诺数Re呈正相关(图4)，随着雷诺数Re逐渐变大，水流由层流转变为紊流，且越接近管道出口，滞留时间越短，其流速越快。

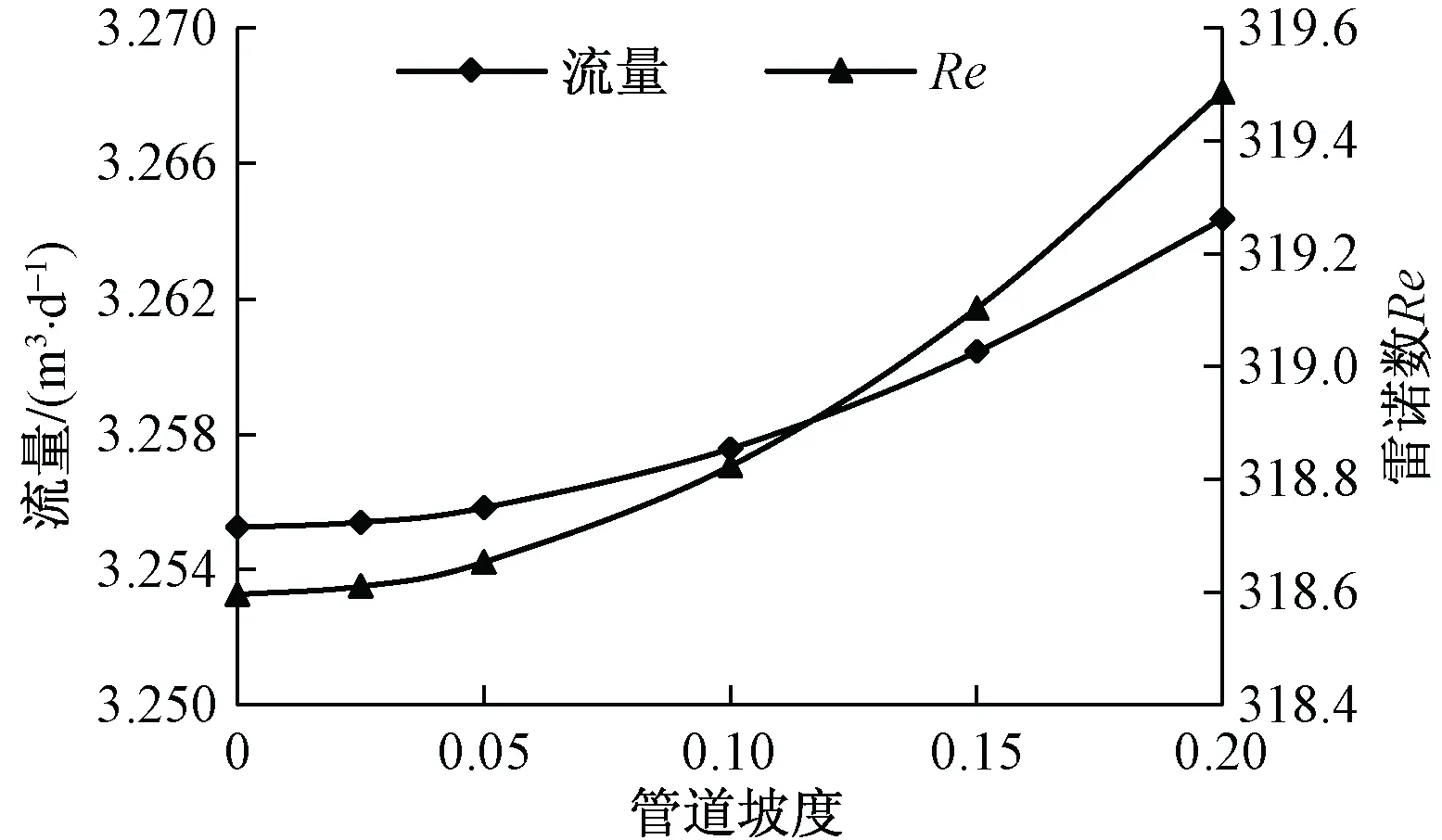
图4 不同管道坡度模拟结果变化曲线Fig.4 Variation in slope simulation results for different pipelines

(4)管道弯曲度

将岩溶管道水平置于含水层中，并保持不变。随着弯曲度的增大，管道流量先增加再稳定后减小(图5)。当管道弯曲度为50时，管道流量达到了峰值。随着弯曲度的增加，管道越来越长，管壁面积越大，即管道水流交换面积越大，从而使含水层中更多水的流入管道，进而使管道流量增大；同时随着管道弯曲度的增加，管道也越来越曲折，使得管道水流受阻，流速越来越慢。当流量达到峰值之前，前者对流量的影响起主导作用，而达到一定程度后，后者对流量的影响更大。

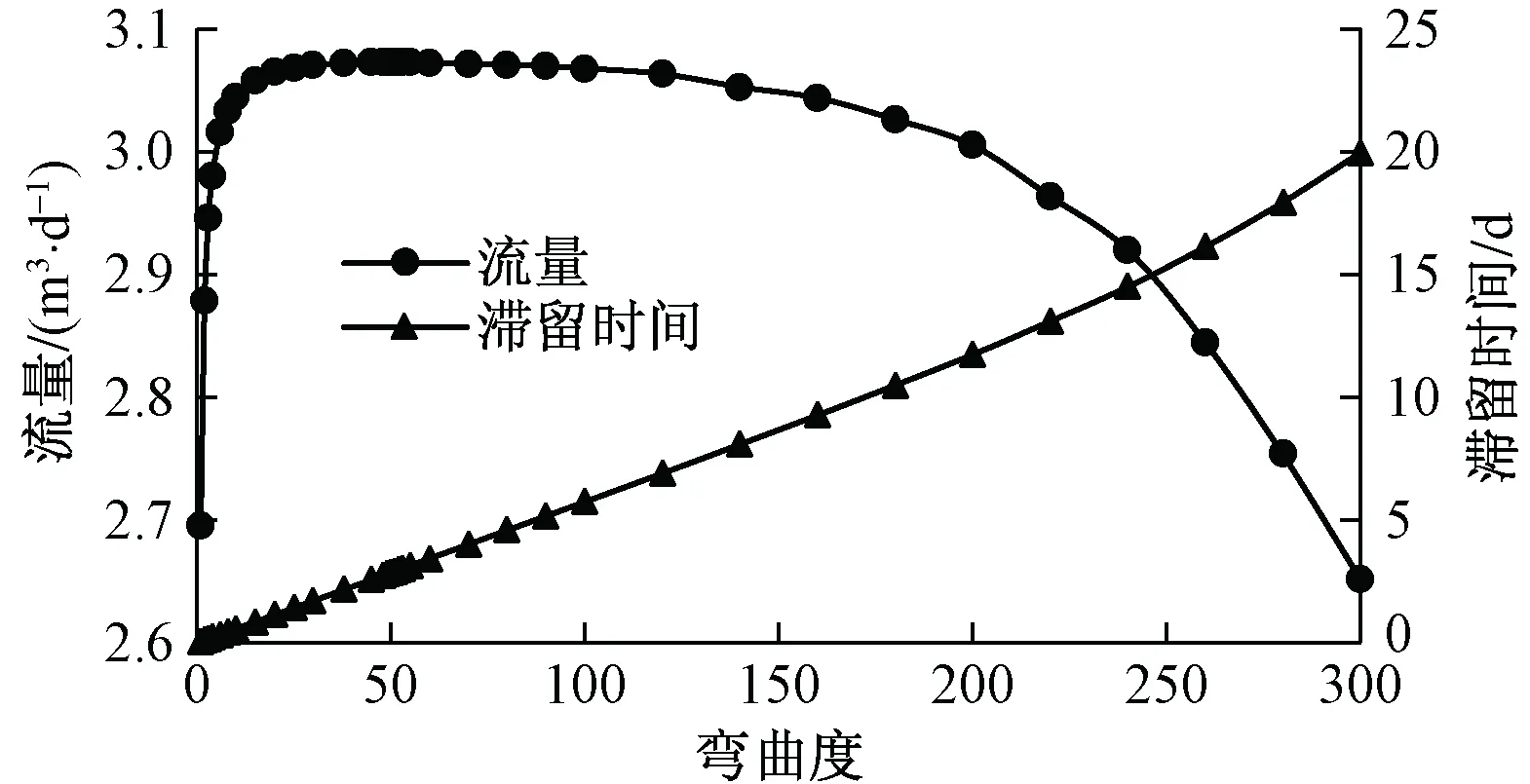
图5 不同弯曲度模拟结果变化曲线Fig.5 Simulation results for different bending degree

(5)管壁渗透系数

当其他管道参数均保持不变时，管壁渗透系数与管道流量及雷诺数Re呈正相关(图6)，由图可知管壁渗透系数在0～3 m/d之间时，流量增长速度较快，呈线性关系：Q=1.6α+0.9(R2=0.88)；当大于3 m/d，流量增长缓慢，并趋于稳定，雷诺数Re具有相似的变化规律。管壁渗透系数较大时，其不再是影响含水层与管道之间水流交换的主要因素，这与Reimann的研究结果相一致[17]。

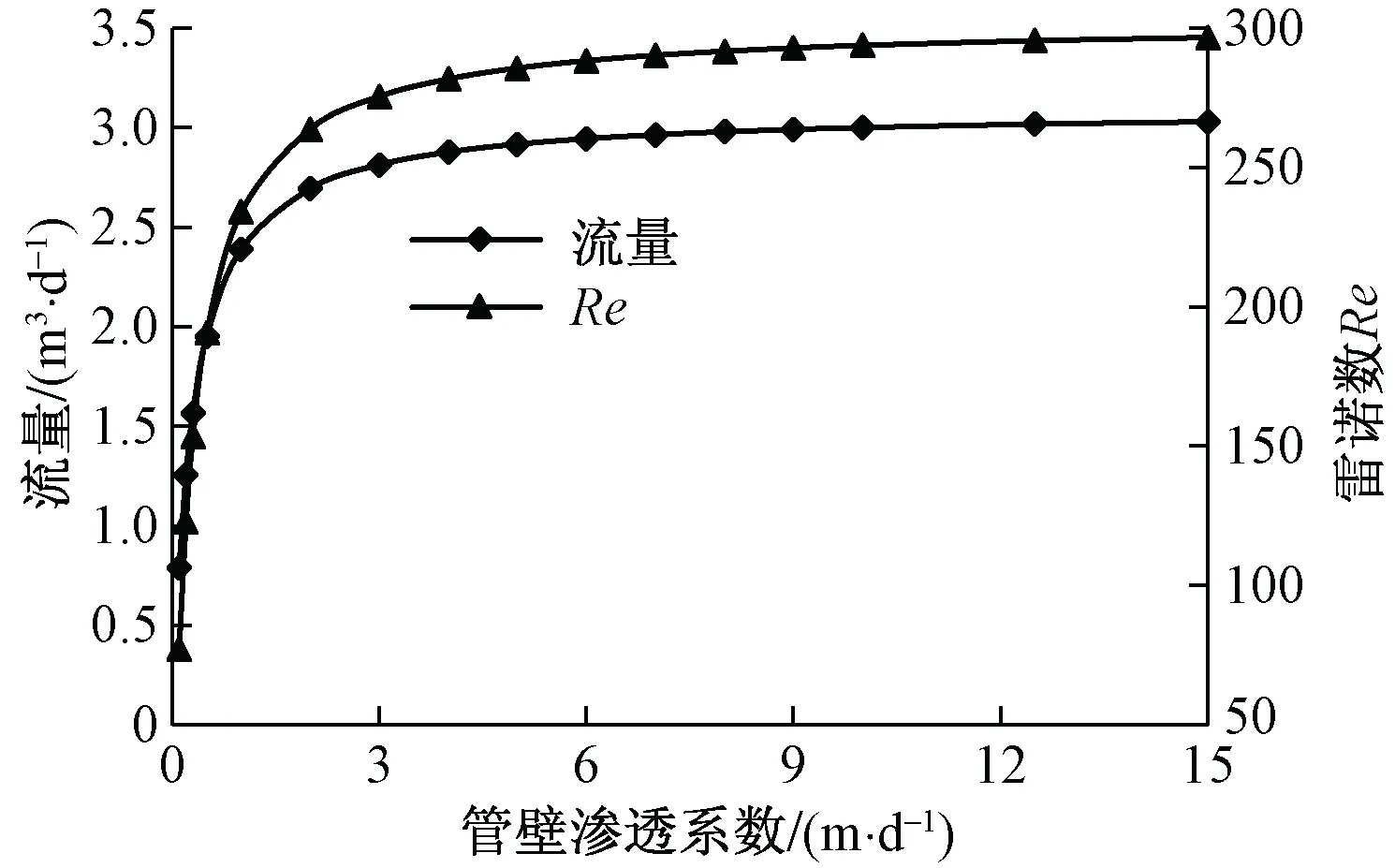
图6 不同管壁渗透系数模拟结果变化曲线Fig.6 Simulation results for different coefficients of permeability of pipe wall

(6)管壁粗糙度

通过管道流模型分析了管壁粗糙度对流量的影响，发现粗糙度整体上对管道流量的影响并无特定规律，粗糙度较小时流量上下波动(图7)，特别是当管壁粗糙度小于0.001 m时，流量波动比较明显。在粗糙度小于0.001 m范围内共做了12组数值模拟，其中有6组管道流量均为2.696 m3/d，而粗糙度在0.001～0.1 m之间时，管道流量虽有波动，但整体上管道流量是减小的。这与管壁粗糙度的增大导致管道内径空隙减小有关，至于管道流量的波动，可能是管道中地下水流动状态(如由层流变为紊流)改变时，导致管道流量突变。在实际岩溶管道中，由于含水层不同位置管道粗糙度不同，地下水流态可能会发生变化，致使在降雨量不变时泉流量也会产生波动，但这种波动较小，常规的观测不易察觉，同样Bahrami指出相对粗糙度小于3%时其影响可以忽略[18]。

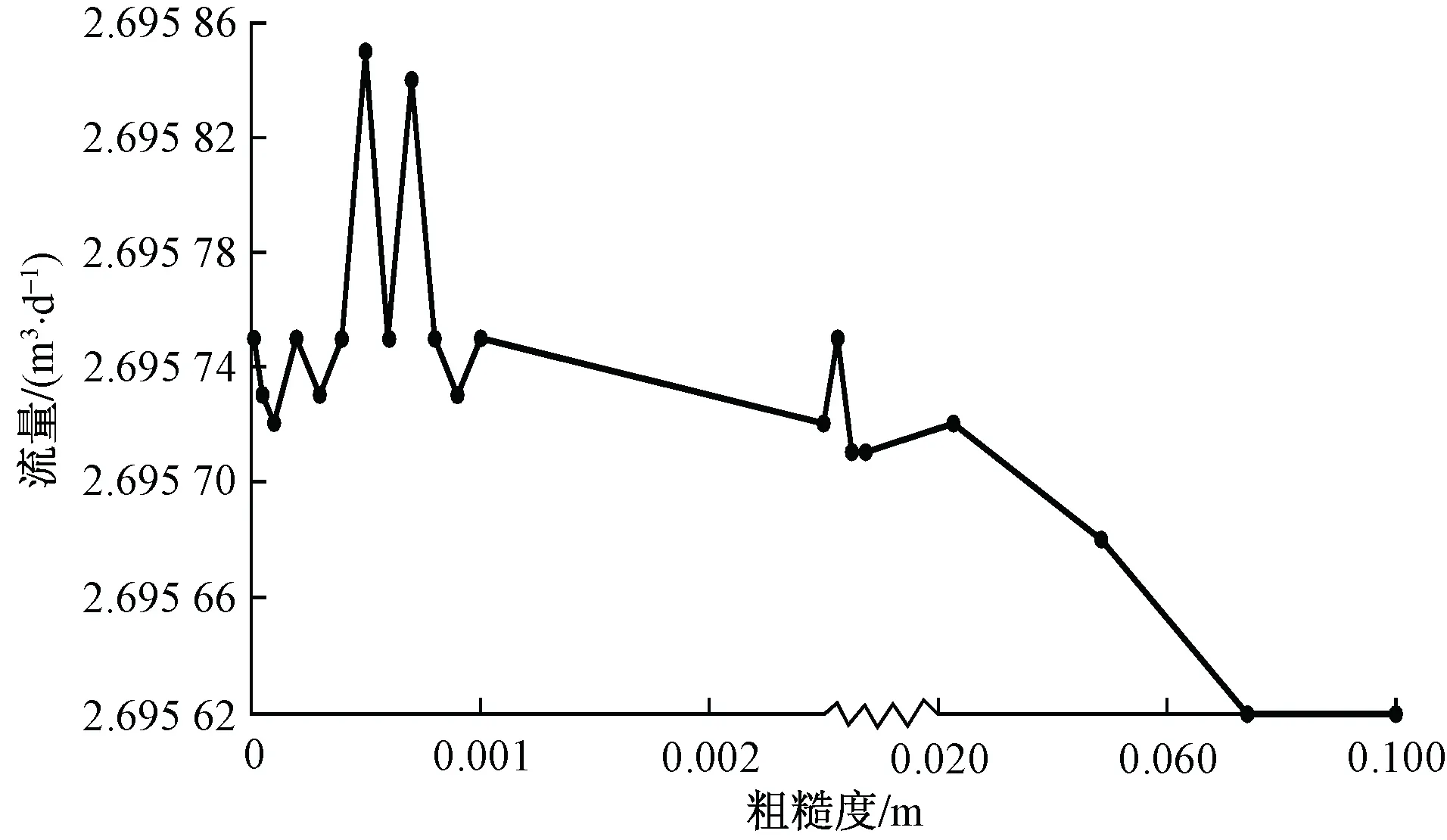
图7 管道流量随管壁粗糙度变化曲线Fig.7 Pipeline flow vs. pipe wall roughness

1.2.2灵敏度分析

用管道流量变化量与对应的参数值变化量的比值作为灵敏度系数，通过对比不同参数灵敏系数，得出特定管道参数对管道流量的影响程度。选取渗透系数为1 m/d、粗糙度为0.001 m、弯曲度为10、管道坡度为0.1、埋深为4.5 m、管径为0.3 m为基础参数，将基础参数值的±80%作为分析区间进行灵敏度分析。经灵敏度分析发现不同参数对管道流量的影响程度差别很大，其中渗透系数和埋深对管道流量影响最大，灵敏度最高；弯曲度和管道坡度次之；管径和粗糙度灵敏度最低。虽然在管径较小时流量发生了一次突变，然而选取区间内的其他管径对流量影响却很小，因此管径的敏感性也较低，影响程度最小的是管道粗糙度，在选取的区间内管道流量几乎不变(图8)。

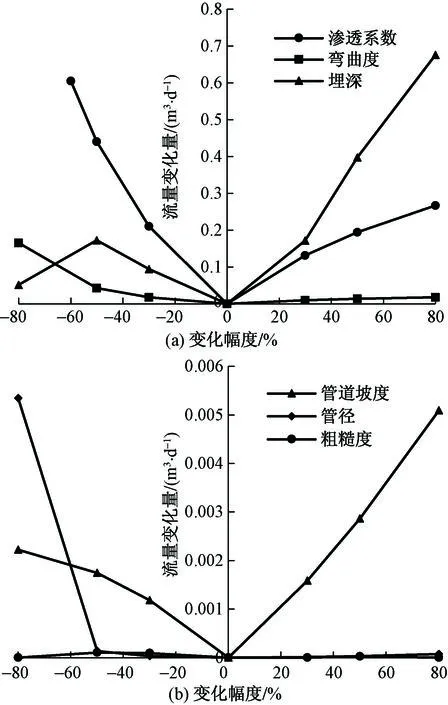
图8 各管道参数对流量影响的灵敏性分析Fig.8 Sensitivity analyses of the influence of various pipeline parameters on flow

管道参数敏感性分析结果为采用CFP模型解决实际问题时管道特征参数的选取提供了依据。

2 许家沟泉域地下水数值模拟

2.1 泉域水文地质概况

许家沟泉域位于河南省鹤壁市，太行山东麓，东邻华北平原，地势西高东低[19]，区域内地表高程由西部600 m逐渐过渡至东部的120 m。西部为纵贯南北的基岩山区，山岭连绵，峰巅险峻，东西向沟谷横切山区，谷深壁陡，迂回曲折，形成山陡谷狭、岗洼相间的典型岗丘地形，泉域面积249 km2，多年平均蒸发量1 467.7 mm。根据鹤壁市气象站的降雨量资料，年最大降雨量达到1 392.8 mm，最小降雨量为266.6 mm，年降水总量在600 mm左右。泉域内河流均属海河流域卫河水系，除淇河为常年性河流外，其它均为季节性河流。淇河是研究区内最大河流，长约150 km，多年平均流量12.53 m3/s，历年瞬间最大流量5 590 m3/s，历年最小瞬间流量0.68 m3/s[20]。

2.2 概念模型

许家沟泉域以奥陶系灰岩含水层为主，其岩溶发育较强烈，是本次模拟的主要含水层。泉域东边界为近SN向延伸的奥陶系灰岩与二叠系泥岩、古近系和新近系砾岩深部接触带，阻碍了奥陶系岩溶水向东运动，是一条相对隔水的边界；南边界与水峪—形盆断裂走向一致，其断层切割寒武系中统徐庄组页岩—奥陶系中下统灰岩、白云岩地层，形成了一条阻水边界；西边界南段大致与盘石头背斜轴部走向一致，出露的寒武系中下统砂页岩与岩溶含水层接触，起到隔水作用，西边界北段与地表分水岭吻合，视为地下分水岭边界；北边界为小南海泉域与许家沟泉域的地下水分水岭(图9)。整个泉域可以概化成无压-承压混合含水系统。前期勘探资料显示，在碳酸盐岩与碎屑沉积岩接触带鹤壁集—鹿楼—许沟形成南北向强径流带，该径流带上多数钻孔揭露有直径0.2～0.5 m的溶洞；此外，修建鹤壁电厂时物探结果显示，淇河北部出现一NWW—SEE向的低阻异常区，后经钻探验证为宽大的溶蚀裂隙。这为构建等效多孔介质-管道模型提供了依据。

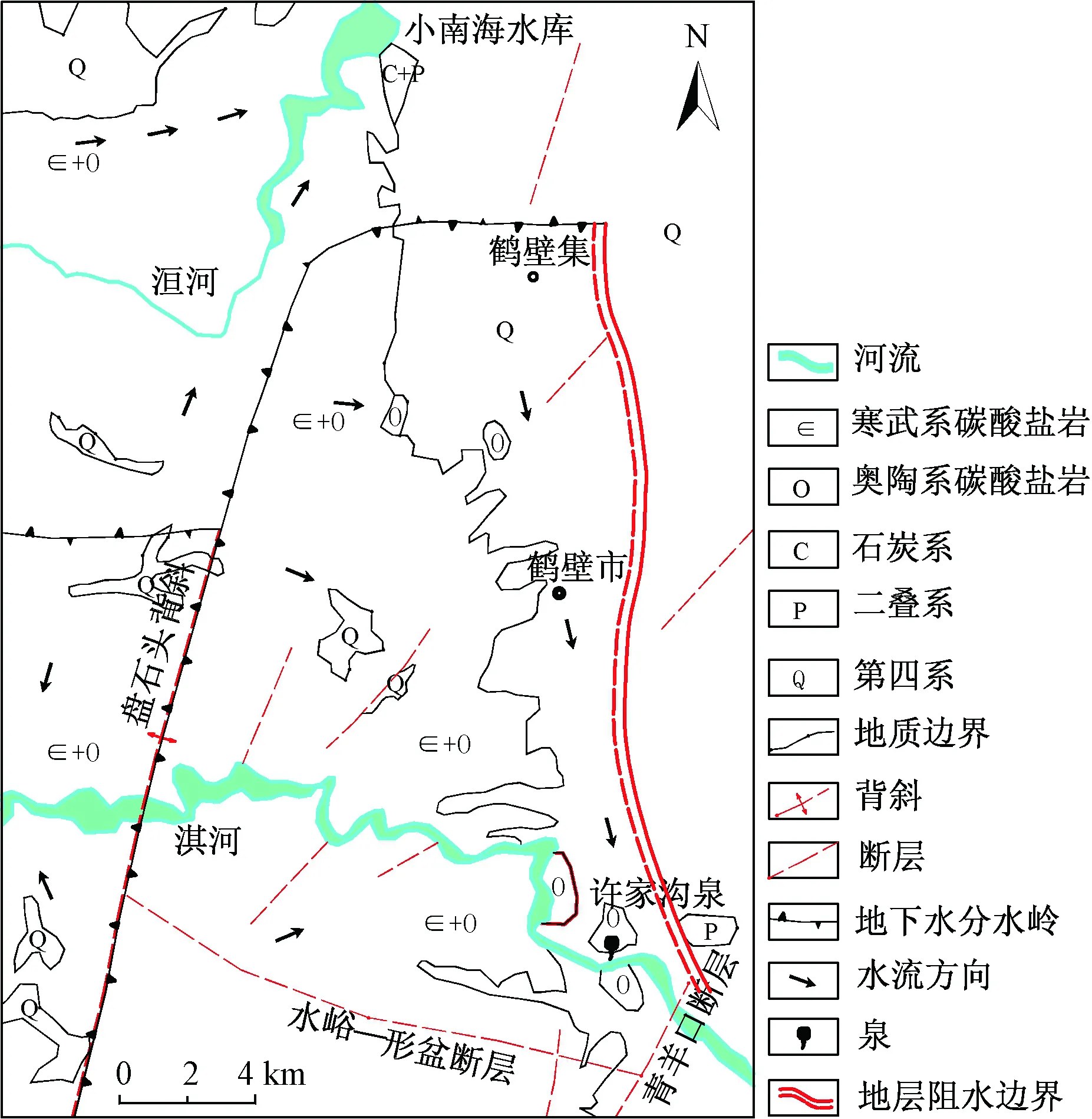
图9 鹤壁许家沟泉域水文地质概图Fig.9 General hydrogeological map of the catchment area of the Xujiagou spring in Hebi

2.3 数值模型

根据研究区水文地质概念模型，建立岩溶管道流数学模型如下：

式中：Kxx、Kyy、Kzz——渗透系数在x、y、z方向上的分量/(m·d-1)；

H0——地下水初始水头/ m；

W——单位时间从单位体积含水层流入或流出的水量，即源汇项/ d-1；

Ss——孔隙介质的贮水率/ m-1；

t——时间/ d；

Ω——模拟区范围；

Γ2——第二类边界；

Q——管道流量/(m3·d-1)；

d——管道直径/m；

Δl——管道长度/m；

v——运动黏滞系数/(m2·d-1)；

Δh——管道水头损失/m；

τ——管道弯曲度；

kc——管道粗糙度/m。

模拟模型依据北京54坐标建立坐标系，对研究区进行网格剖分，剖分成正方形网格，沿x方向上剖分55列，沿y方向剖分102行，在垂向上分为1层，每层为等长等宽不等厚的六面体单元，每个单元网格大小为250 m×250 m。根据勘探资料确定了水文地质参数分区及岩溶管道位置(图10)，耦合了9条岩溶管道(表1)，其中管道5与许家沟泉直接相连，节点6设置为定水头112 m，与泉口标高保持一致，结合泉域岩溶水文地质条件，构建了许家沟泉域的MODFLOW-CFP模拟模型。

模型以2015年6月地下水流场作为初始流场，参数以勘探时抽水试验结果数据为初值，利用半年的观测资料，经调参识别与校正(图11～12)，得出如表2所示的水文地质参数。

图10 MODFLOW-CFP模型中水文地质参数分区及管道位置分布Fig.10 Division of hydrogeological parameters and location of pipelines in the MODFLOW-CFP model

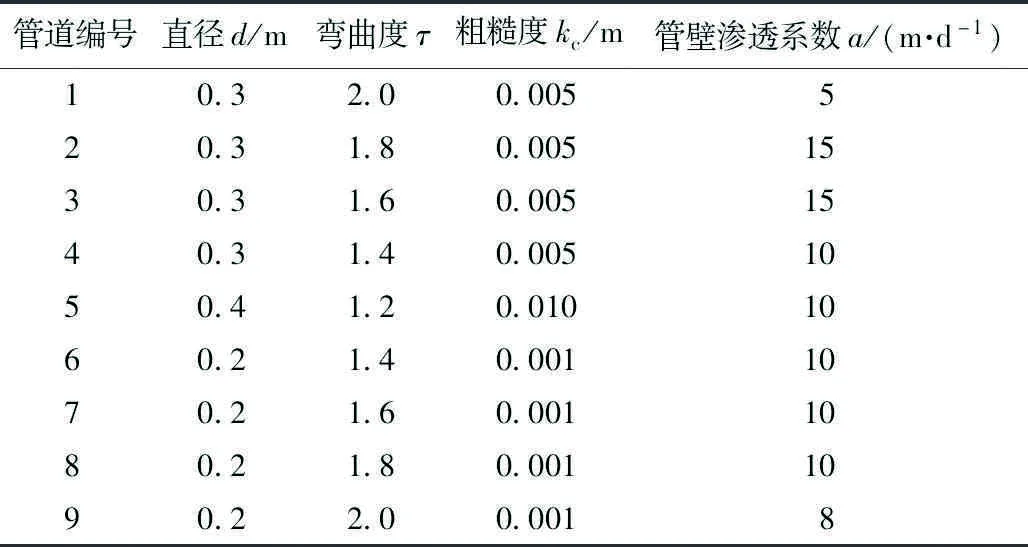
表1 岩溶管道参数Table 1 Karst pipeline parameter characteristics

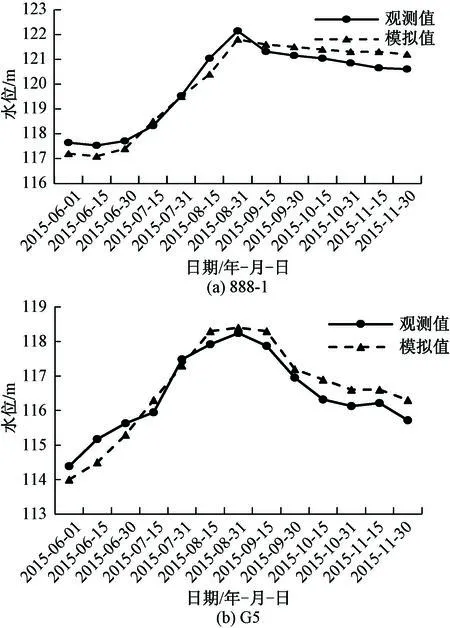
图11 观测孔模拟计算值和实测值对比曲线Fig.11 Comparison of the simulation values and the measured values at the observation hole

图12 岩溶地下水流场拟合图Fig.12 Fractal map of the karst groundwater flow field

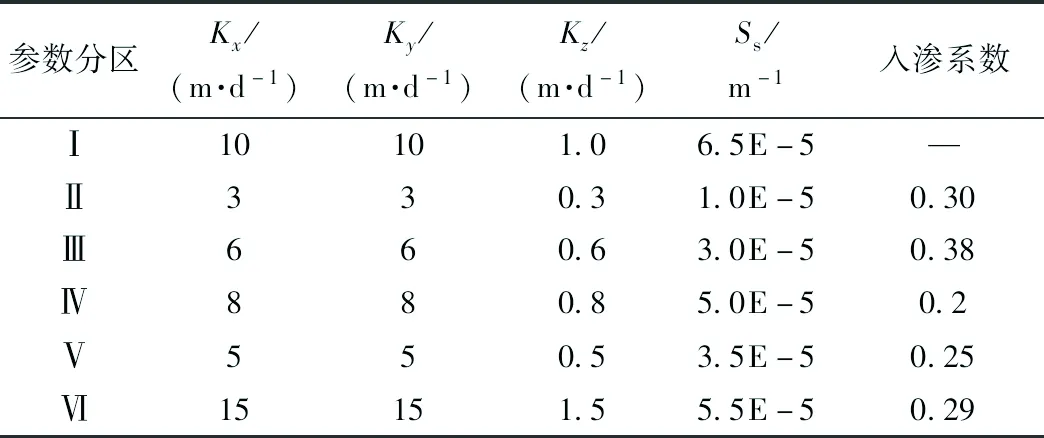
表2 含水层参数设置及分区Table 2 Aquifer parameters setting and zoning

图13为泉流量实测值与模拟值对比曲线，结果显示，模拟值略小于实测值，且模拟的泉流量峰值有所提前。在实际中，降雨受岩溶含水介质特征的影响，泉流量会存在滞后效应，这一点在模型中虽也有体现，但滞后效应并不明显，可能与管道坡度、管壁粗糙度及弯曲度的取值有关。虽然管径和埋深可根据钻井资料确定，但管道弯曲度和管道坡度却不易获得。整体上看，模拟计算水位与实测地下水水位基本一致，地下水流场拟合效果良好，模型较符合实际。

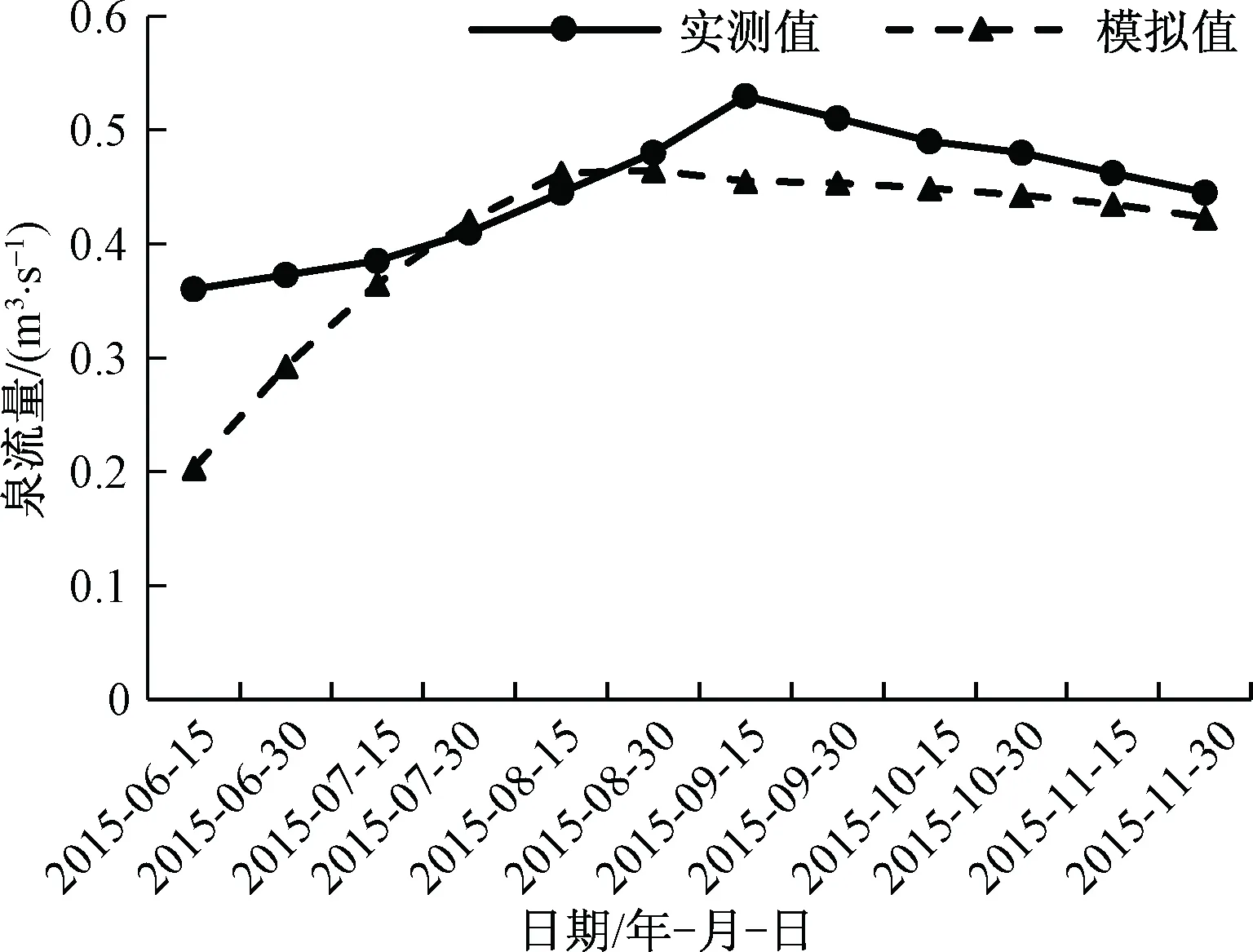
图13 泉流量实测值与模拟值对比曲线Fig.13 Comparison of measured values and the simulated values of the spring discharge

2.4 不同降水保证率下预测泉流量

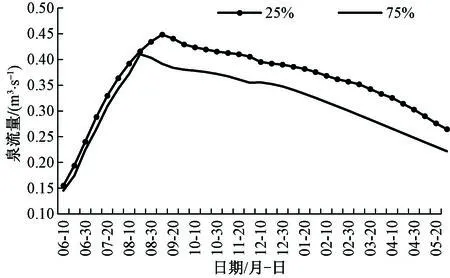
图14 预测的泉流量动态变化曲线Fig.14 Predicted dynamic changes in the spring discharge

依据1966—2016年降水量资料，确定了不同降水保证率下的降水量以及各月平均降水量及其占年均降水量的百分比，而将不同降水保证率所对应的年降水量乘以该比例系数，得出每月的降水量，并分配到所构建的模拟模型中，预测不同降水保证率下泉的出流量。保持开采量不变，将25%降水保证率对应的年降水量作为丰水年进行分析，结果显示(图14)：丰水年泉口水位约为114～115 m，高出泉口附近标高2～3 m，年最大泉流量为0.45 m3/s，平均泉流量为0.36 m3/s；将75%降水保证率对应的年降水量作为枯水年进行分析，结果显示：枯水年泉口水位约为113 m，略高于泉口标高112 m，年最大泉流量为0.41 m3/s，平均泉流量为0.31 m3/s。

借助该模型探讨了不同降水保证率下降雨量对泉流量影响，根据模型运行结果可知：虽然枯水年泉流量相对丰水年较小，但也保持了较好的流量溢出。说明降雨量在一定程度上影响了泉流量，但不是许家沟泉继续溢出的决定性因素。近年来许家沟泉域水位有所下降，许家沟泉流量也有衰减趋势，很大程度上是由于对地下水开采量增加导致的。

3 结论

(1)管壁渗透系数、管道坡度和管径与管道流量呈正相关。当管壁渗透系数和管径较小时，其对管道流量的影响较大；反之，当该参数较大时，对流量影响较小。随着管道弯曲度和埋深的增大流量和雷诺数先增大后减小，存在峰值。管壁粗糙度对流量和雷诺数影响较小，且呈现出一定的波动性，特别是在管壁粗糙度较小时，波动比较明显。

(2)岩溶系统流量对管壁渗透系数和埋深的敏感性最高，其次为弯曲度和管道坡度，而管道直径和管壁粗糙度的敏感性最低。

(3)构建的MODFLOW-CFP模型较符合许家沟泉域岩溶水文地质条件，模型预测结果显示：在25%降水保证率下，许家沟泉域年最大泉流量为0.45 m3/s，平均泉流量为0.36 m3/s；在75%降水保证率下，年最大泉流量为0.41 m3/s，平均泉流量为0.31 m3/s。