针对小规模数据集的多模型融合算法研究

李春生，曹 琦，于 澍

(东北石油大学 计算机与信息技术学院，黑龙江 大庆 163318)

0 引 言

机器学习作为人工智能的重要研究内容，经过半个世纪的发展，现今已和模式识别、数据挖掘、统计学习、计算机视觉、自然语言处理等多个领域相互影响、交织发展[1]。

集成学习目前是机器学习领域中的一种研究方向。使用弱学习器通过多模型融合的思想可以极大提高准确率。当前集成学习(Bagging)主要使用弱学习器，且为同类模型，例如随机森林使用多棵深度较浅的决策树，在构建Bagging集成的基础上将决策树作为基学习器[2]，最终进行投票获得最终结果。文中尝试使用多类强学习器进行模型融合，并与单一强学习器进行指标对比。

1 相关研究

1.1 决策树模型

决策树是一个有监督的机器学习算法，常用于分类预测等诸多领域，由于其高效性、误差小的优点，在分类问题中得到了广泛的应用。在决策树中，内部分支节点表示一个条件属性，而叶子节点表示一种决策属性或分类结果[3-5]。决策树是一个预测模型，其叶节点代表最终样本分类，各属性划分代表分类规则。

由于文中解决二分类问题，选用当前较为流行的C4.5算法作为其中一种基类模型，C4.5算法是由J.Ross Quinlan开发并且用于决策树的算法[6]。C4.5算法流程与ID3类似，相比ID3，将信息增益改为信息增益比，选择信息增益比大的特征当作决策树的节点并不停递归构建决策树，同时设置阈值避免过拟合。主要公式如下：

数据集S的信息熵：

特征F对于数据集S的条件信息熵：

特征F的信息增益：

Gain(S,F)=H(S)-H(S/F)

特征F对数据集S的分裂信息：

特征F对数据集S的信息增益比[7]：

1.2 逻辑回归模型

逻辑回归(logistic regression)是一种可以用来分类的常用统计分析方法，并且可以得到概率型的预测结果，属于一种概率型非线性回归[8-10]。逻辑回归是经典的分类模型，它将模型拆分为线性部分和激活函数，主要公式如下：

假设x为输入变量，W为权重矩阵，B为偏置，A为线性部分输出，则线性部分函数为：

A=Wx+B

激活函数使用sigmoid函数，将线性部分输出A当作sigmoid函数输入值，y为预测结果：

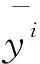
通过使用梯度下降或者mini-Batch梯度下降等算法完成对模型损失函数的迭代，最终给出权重W和偏置B。

1.3 SVM模型

文献[11-15]指出支持向量机(support vector machines，SVM)是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机。文中选用线性可分支持向量机，通过核函数与软间隔最大化，学习得到分类决策函数：

其中K(x,xi)为正定核函数，使用序列最小最优化(sequential minimal optimization，SMO)算法实现支持向量机的优化过程。SMO算法要解决的是凸二次规划的对偶问题：

SMO基本思路为选择两个变量，固定其他变量，针对这两个变量构建一个二次规划问题，这时子问题可以极大提高算法的运算速度。SMO算法将原问题不断分解为子问题并对子问题进行求解，进而达到求解原问题的目的。

2 多模型融合算法

2.1 基本思想

多模型融合算法思想与Bagging集成学习算法思想类似，对比Bagging集成学习将弱学习器当作基学习器，使用平均投票得出最终结果的方式。文中提出的多模型融合算法使用强学习器决策树、逻辑回归、SVM作为基学习器，并将基学习器输出当作下一阶段的输入，加入权重矩阵并使用最大似然估计迭代优化参数，计算出基学习器模型的输出权重参数，从而完成多模型融合过程。

2.2 算法描述

多模型融合算法共分为两部分：基学习器训练、基学习器权重训练。

第一部分：

输入：训练数据集T={(x1,y1),(x2,y2),…,(xN,yN)}；各基学习器损失函数{L(y,f(x))}；基学习器集{b(χ;γ)}；

输出：各基学习器模型{f(x)}。

(1)初始化各f(x)。

(2)针对各个基学习器极小化损失函数：

min(Loss(y,f(x)))

(3)更新基学习器模型参数。

(4)得到{f(x)}。

第二部分：

输入：训练数据集合T={(x1,y1),(x2,y2),…,(xN,yN)}；第一部分已经训练完成的基学习器模型，MSE损失函数；

输出：各基类学习器权重参数。

(1)初始化权重矩阵W，初始化多模型融合函数：

fall(x)=w1×fLR(x)+w2×fTree(x)+w3×fsvm(x)

(2)目标函数:

(3)最终输出各基学习器参数与对应权重。

3 实 验

3.1 数据分析

文中使用泰坦尼克号之灾数据集验证算法效果。泰坦尼克号之灾是Kaggle上经典的二分类问题，造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管幸存下沉有一些运气因素，但有些人比其他人更容易生存，比如女人，孩子和上流社会，通过分析数据，使用机器学习模型，判断乘客能否存活。通过最终结果表明，该数据集可以有效检验各模型性能对比情况。

泰坦尼克号之灾数据集共有训练数据891条，有12列属性，其中Cabin属性由于缺失值占比过多，将属性值转化为有值(yes)，无值(no)，同时使用众数补偿Age中Null值。属性信息如表1所示，训练数据如图1所示。

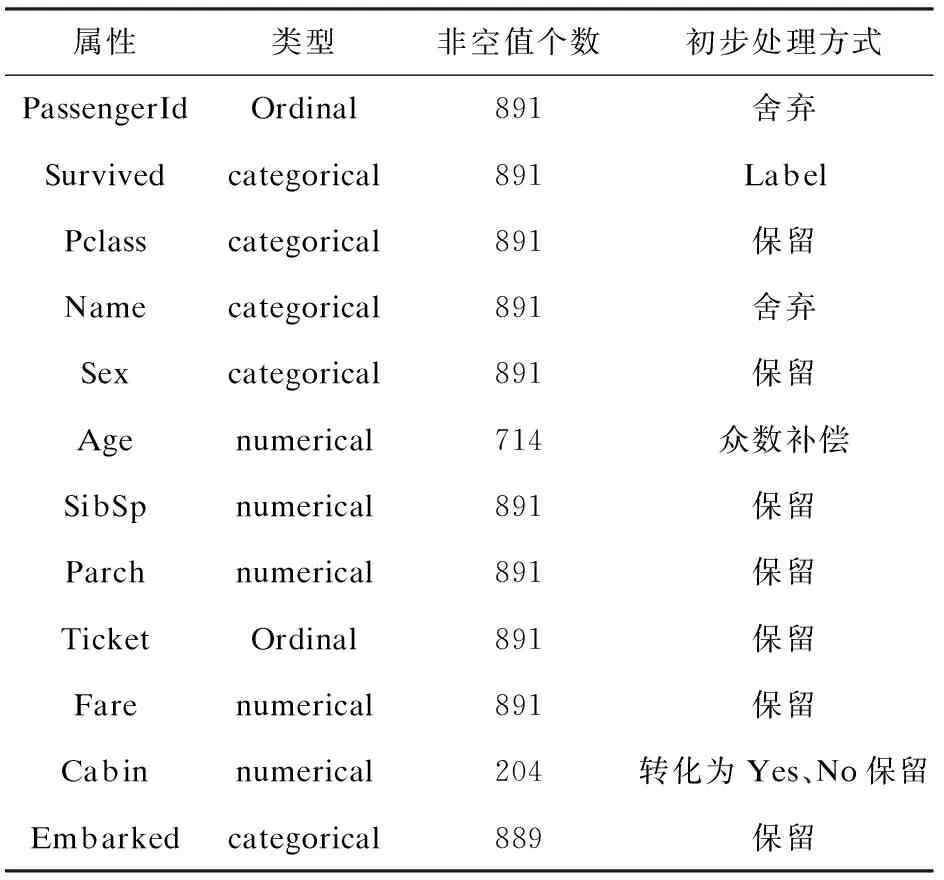
表1 属性列表

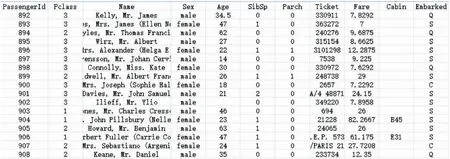
图1 训练数据

针对所有保留属性创建与label变量的映射图，直观观察变化关系，剔除无明显相关关系的属性，使用保留属性建立特征集合，对离散特征进行因子化，对连续特征进行归一化操作，最终生成特征变量，部分有效属性与label对应关系图如图2所示。在图中可以明显观察出Age、Sex等变量与label相关性强，而变量Name、Ticket由于是随机化数据从而导致与label无明显关系。

图2 部分变量与Label对应关系

3.2 评价指标

评价模型指标有多类，由于文中为二分类问题，所以选用精确率、召回率、准确率、ROC评价模型性能。

精确率(Precision)指的是模型输出结果中判断为正样本的数据中真实为正样本的比例。

召回率(Recall)指的是有多少正样本被准确标出。

设模型输出的正样本集合为A，真正的正样本集合为B，则有：

准确率(Accuracy)衡量的是分类正确的比例。假设是y＾是模型输出的预测label，y为样本中正确的label，则准确率为：

ROC曲线是以假正率为横坐标，真正率为纵坐标的曲线图。设模型预测的正样本集合为A，真正的正样本集合为B，所有样本集合为C，则A与B的交集个数除以B的个数为真正率(true-positive rate)，A与B交集的个数除以C减B的个数为假正率(false-positive rate)。AUC(area under curve)分数是曲线下的面积，越大意味着分类器效果越好。

3.3 实验结果与分析

在表2实验数据指标中列举出各个模型在测试集中的评价指标，并增加神经网络与多模型融合进行横向对比，通过对比得出，多模型融合算法在精确率、召回率、准确率、AUC各个指标上均有明显提升。相对于神经网络这类深度学习模型，多模型融合算法更加适用于小规模数据集。

表2 实验数据指标

4 结束语

在小规模数据集合中，多模型融合算法可以融合各个模型优势，对基学习器预测正确结果给予更大权值，对预测错误结果减小权值，通过数据累加，最终增大模型预测准确率，同时提升模型各项指标。相对于深度学习模型需要大量数据进行训练，多模型融合算法更加适用于小数据集。文中在特征选择中并不完善，后续可以通过特征组合等方式进行提升。