在计算教学中培养小学生的数学建模意识

钟斌

【摘要】数学知识的探究、归纳、总结与交流活动有利于锻炼小学生的反思、交流与提炼的数学思想。在教学中培养小学生建立数学模型的思想，让学生联系生活实践来创设情境、感知数学模型，在探究、交流融合之间提炼数学模型，让学生在互动交流、相互纠错的过程中体验彼此数学思维的异同，多角度的探讨数学思想的过程中感受数学模型的价值。

【关键字】计算数学 探究归纳 数学建模

【中图分类号】G623.5

【文献标识码】A

【文章编号】1992-7711（ 2020） 06-119-03

数学问题是学生在探究、认识新知识、总结深化并运用新知识的目标定向。小学数学的建模是通过让学生探究新知识的生成背景、新旧知识的融合点、联系具体的生活情境凝练出数学问题，在探究归纳新知识的过程中领悟数学思想，在感悟过程中创造、交流、总结数学知识，促使学生在解决问题的过程中建立起数学模型思想。数学建模可以有效地帮助学生建立起数学知识系统，激活学生的认知系统，让学生在创造数学、交流数学以及相互反馈、融会贯通数学原理的过程中发散数学思维，提高学生的思维探索能力以及数学模型意识。

《义务教育阶段的数学课程标准》强调：“要从学生已有的生活经验出发，让学生亲身经历将实际问题抽象成数学模型，并加以解释与应用，进而使学生在思维能力、情感态度与价值观等多方面得到进步和发展”。现代信息技术的迅速发展、普及为教育工作者和学生的思维方式、学习模式以及建立小学数学模型等提供了有力的支撑。学生在创设新知识的数学情境、呈现数学问题、创造属于自己的数学模型，探究总结数学知识的过程中，利用信息技术，彼此间相互交流、分享知识的见解，在相互的思维碰撞之间知错、思错、纠错、融会贯通知识，最终建立起数学模型思想。

一、借助“小微课”，呈现计算的思维过程，感知数学建模

数学问题的产生往往来源于实际生活的需要，而学生探索知识、破旧立新则是通过以往的知识与自己的认知结合起来，然后去总结、验证新知识、梳理清楚数学知识的原理、规律，在探究中凝练出具体生活情境中的数学，了解生活中的数学，最后将生活中的数学提炼、创造，形成自己的数学模型，初步地感知数学建模的思想。而信息技术的发展普及，尤其小微课，它所具备的短小精悍、容量丰富以及碎片化的知识集中清楚的特点，可以清楚地将学生构建感知数学模型的细微过程融合展现。

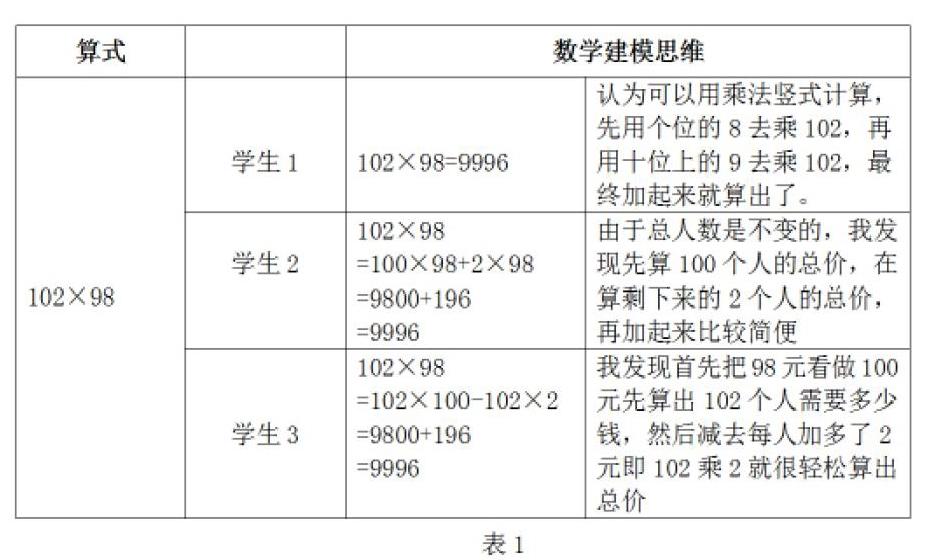
学生只有亲历数学建模的过程，从生活的情境中去体验数学化的模型，才能对数学建模感兴趣。因此在教学运算律计算的时候，我便以孩子们最感兴趣的亲子游为数学问题的产生情境：周六班级举行亲子游活动，每人需要102元，大小同价，我们班共98人报名参加，那么一共需要多少元？

孩子们对于这样的数学问题非常感兴趣，我趁势引导孩子们制作小微课视频，将自己分析问题的过程、寻找或者创造适当的解决方法记录下来，初步地感知数学建模思想，进而将自己的建模过程与同学之间分享交流、对比验证融合彼此的建模思想。

数学建模需要学生把实际问题归纳总结成数学模型，将自己的数学知识与生活化情境结合，主动参与探究，在探究的过程中形成自己的数学建模思想。通过先进的信息技术一一小微课呈现自己如何建立“人数与单价”之间的数学模型，交流彼此的数学建模过程，感受到数学建模带来的成就感。通过小微课的呈现为纽带，融合彼此的数学建模思想，在提升自我数学建模能力的同时享受数学源于生活，服务于生活所带来的乐趣。

二、借助信息技术，梳理知识结构，建立数学模型

小学生对于身边直观的生活情境情有独钟，很善于从中观察分析有关数学信息，将数学信息进行处理，然后从不同的角度去思考、用不同的方式去诠释实际生活中的数学知识，理解数学内涵，最后用数学符号语言来建立起属于自己的数学模型。

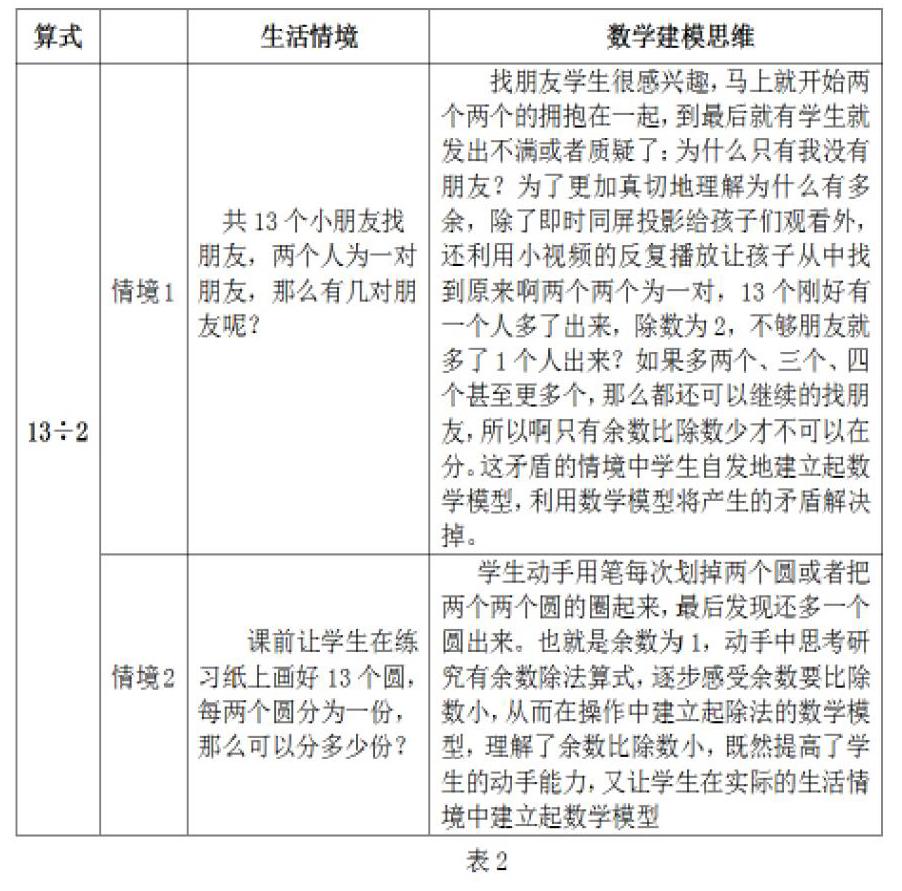
在人教版小学数学三年级上册《有余数的除法》时候，如果直接揭示被除数，除数，商和余数之间的关系，直截了当地告诉学生余数必须比除数小。那么学生由于没有体会到除法的产生背景与应用价值，对“余数必须比除数小”这一关键点就有疑惑：为什么余数一定比除数小？为了顺利地帮助学生突破难点，引导学生从实际的生活情境中建立起数学模型，我引导他们利用信息技术，比如同屏技术、小微课等即场呈现甚至反复重现学生的即时思维建模过程。

通过利用信息技术達到反复观摩引导、对比分析、归纳总结初步建立起2的倍数以及余数比除数小的模型后，可以利用小微课准备好的21个小朋友，每4个小朋友围一个圈，可以围成几圈？如果5个小朋友围一圈呢？6个小朋友围一圈呢？在2的倍数基础上不断地让学生运用建立起来的数学模型延伸运用，逐步地感受除法各部分之间的联系，这样学生学得有兴趣，对建立数学模型也就更感兴趣。

三、重本求源，合作交流，亲历数学建模

小学生局限于生活经验少，基础知识储备相对比较单薄，分析抽象内容，概括抽象内容能力相对薄弱，但他们的生活实际操作能力强，善于从操作中感受出隐藏的数学问题，并且用数学的语言符号与方法将抽象的内容简便表述出来，建立起数学模型。

比如小学数学中的《方程》是在以往整数、小数计算模型的基础上的一次华丽转身。方程是在学生掌握理解了四则运算以及会用字母表示数的基础上展开学习将已知的数据与未知的数据有机结合，是个新的抽象知识，对学生的数学思维建模方式有了新的挑战方向，对学生迁移旧数学知识建立新的数学模型能力有很大的提升。

学生在整数计算的建模中已经有了一定程度的经验积累，对于如何分析实际生活中的数学问题、猜测数学结论、验证数学结论、运用数学也有了一定的经验沉淀，因此在教学《方程》，我引导学生小组合作，实践操作，将以往的数学建模思想迁移到新的数学知识上，在实践操作分析思考中建立起方程的数学模型。

（一）观察体验，感知数学模型

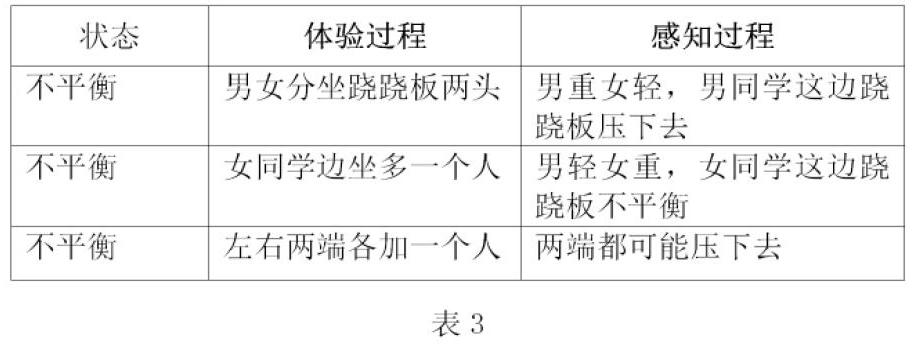
在教室做了个简易跷跷板，随机一男一女同学坐分坐在两头，让学生在兴趣昂然中感受不平衡，体验中感知等式数学模型。

有趣的体验唤醒了学生已往的知识经验，抽象的未知数在跷跷板的平衡与否中变得具体形象起来。这时候学生在两端加坐人的过程中会产生疑惑：坐多重的人才能使跷跷板两端达到平衡？体会到加多少还是未知的，可以用字母或者符号如a、x、y、？…来表示。学生在观察体验跷跷板由不平衡到平衡的过程中，探究用数学语言、数学符号来表达，如80=50+a、80=50+x、80=50+？等，从具体的生活情境中逐步体验未知数，从跷跷板的平衡中去感知方程是等式以及建立起方程的数学模型：

（1）首先是等式。

（2）含有未知数。

（二）实践操作，合作探究，建立初步的方程数模

提出疑惑：含有未知数的方程，怎么解出它的大小？

方程模式是小学生在计算学习过程中的一个重要知识演变，它直接地从整数的计算模型中进入含有未知数的模式，从整数模型之间过渡到方程思想思维。

（1）借助天平秤，合作探究思考，初建数模

小组实践操作：

①当这样天平时：原来这个未知数x=50。

②天平两端都增加变化时：可以将左右两边的30都一起拿掉，那么x=50。

③天平一端这样放：有了前面的模型经验，

学生很快就知道如果左边的30拿掉，那么右边的也相对应地减少30，那么未知数就可以知道。

在这样的实物操作中经历天平两端的加与减的过程中，理解到两端的变化，从实际的问题向数学问题的解决方面转变，同时用数学语言来表达两端的变化规律，建立起初步的解方程模型。

（2）借助信息技术，丰富数学建模内容

学生在实际的问题情境中通过实践探究，迁移旧知识，构建起了初步的方程计算模型。在这样的基础上继续丰富方程计算數模的内涵，提升学生党建模兴趣与能力。而信息技术的普及发展，可以形象地还原、呈现方程计算的过程，利用信息技术的动画等功能帮助学生探究方程计算模型的规律。

学生小组合作探究，引导学生对比挖掘以上几次的变化，给予学生探究的时间机会：如果3X-30=80等又该怎么样呢？学生会自主发现总结：构建方程数模，只要根据天平原理即等式的性质就可进行方程的解答。

（3）拓展延伸，运用数模

在经历现场生活情境，在情境中挖掘数学计算的信息，通过计算建模的过程中提高了解数学，体验数学以及运用数学的建模能力。问题是数学的心脏，探索研究运用知识，梳理知识结构，运用数学模型进行拓展延伸。在基本的方程模型后，学生会产生这样新的疑问：如果是其他的方程模型又该怎么去思考解决？

对于新的15-x=10.15÷x=5的模型，利用多媒体帮的帮助，将新的方程模型一步步剥离还原成旧数模，这样可以提高学生寻求建立新数学模型的动力。

小学数学计算中培养学生的建模能力，通过数学计算的建模，训练着学生的思维能力，提高着学生用数学语言与符号表达建模的过程，有利于提升学生在数学计算学习中建立模型，运用数学模型去解决生活中的实际问题的能力，在学生的学习过程中形成自我的模型构建意识。

【参考文献】

[1]中华人民共和国教育部，义务教育课程标准（2011年版）[S]，北京：北京师范大学出版社.

[2]马丽雅，“数学建模”教学模式在小学数学中的应用[J].课程教育研究，2016（26）：121.