一种基于WPF 方法的SEIR 传染病动力学模型仿真研究
陈 恩,段德光,李 昊,陶学强,高树田
(军事科学院系统工程研究院卫勤保障技术研究所,天津300161)
0 引言
近年来,突发传染病的疫情防控受到国内外高度重视,烈性传染病在防控过程中如果采取措施不当很容易造成大规模的暴发[1-3]。随着全球化的发展,原来仅限于某一地区的疾病可能迅速传播和蔓延,引起社会恐慌、经济衰退等问题。突发性传染病的防治研究已成为全球公共卫生工作的重点和热点[4]。
传染病动力学是用数学方法描述传染病的传播过程,实现对感染人群数量及趋势的预测,从而指导相关部门采取相应的措施来控制传染病的传播。传染病动力学模型可以分为2 类:决定论模型和网络动力学模型。目前决定论模型以微分方程为主,代表性模型有SIR(susceptible-infected-recovered)、SIS(susceptible-infected-susceptible)、SEIR(susceptible-exposed-infected-removed)等[5-7]。SEIR 模型在SIR 模型的基础上增加了潜伏期环节E,是一种更适用于有潜伏期传染病的数学模型。针对传染病SEIR 模型的仿真,曾有很多专家进行深入研究[2],但大部分研究重点是趋势性仿真,将实现短期数据预测作为研究重点的还比较少。
为此,本文以SEIR 模型为基础,结合WPF(Windows Presentation Fundation)编程,以新型冠状病毒肺炎(以下简称“新冠肺炎”)在湖北省传播过程为例,开展传染病动力学模型的数字化、图形化的仿真研究。SEIR 仿真模型可以根据已有疫情数据进行迭代修正参数,实现仿真预测短期数据和长期走势,提升应对传染病疫情的处理能力。
1 基于SEIR 的传染病动力学模型建立
1.1 模型假设
根据新冠肺炎在湖北省实际传播情况,结合Kink 的传染病“四阶段说”,将传染病疫情大致分为征兆期、暴发期、高峰期、衰退期4 个阶段[8]。SEIR 仿真模型针对湖北省新冠肺炎疫情4 个不同阶段进行独立分析,在各个阶段建立有效的控制参数,根据疫情发展进程,采取切实可行的防控措施。为了建立科学可信的传播扩散模型,作出如下假设:
(1)忽略传染病发病期的城市人口自然出生率和自然死亡率,且传染病的持续周期不会很长;
(2)自我隔离可以有效减少传染病传播概率;
(3)不考虑人口大量流动,假设在人口封闭的环境下传播。
1.2 符号定义
本文中所用的符号定义如下:a1为1 名潜伏期人员与1 名易感人员接触感染的概率;a2为1 名确诊人员与1 名易感人员接触感染的概率;b 为潜伏期人员单位时间内恢复为易感人群的概率;c 为潜伏期人群单位时间内确诊的概率;d 为确诊人群单位时间内康复的概率;f 为确诊人群单位时间内死亡的概率;f1为1 名潜伏期人员单位时间内接触人数;f2为1 名确诊人员单位时间内接触人数;N 为总人数,包括易感人群、潜伏期人群、确诊人群、康复人群和死亡人群。
1.3 模型建立
社会人群可以分为以下5 类:
(1)S类:称为易感人群,该类成员没有染上传染病,但缺乏免疫能力,可以被染上传染病;
(2)E类:称为潜伏期人群,该类成员已经染上传染病,而且可以传染给S 类成员;
(3)I类:称为确诊人群,该类成员已经染上传染病,而且可以传染给S 类成员;
(4)R类:称为康复人群,失去传染能力;
(5)D类:称为死亡人群。
S(t)、E(t)、(It)、R(t)、D(t)分别表示t 时刻上述5 类人群数量。
变量S(t)、E(t)、I(t)、R(t)、D(t)视为连续变量,并可进一步连续可微。假设人群中S(t)、E(t)、I(t)、R(t)、D(t)成员均匀分布,传播方式为接触和飞沫传播。单位时间内1 名确诊者与他人的接触感染的概率为a2,接触人数为f2,则1 名确诊者在单位时间内与S 类成员接触传播人数为f2×a2×S(t)/N,同理,1 名潜伏期人员在单位时间内与S 类成员接触传播人数为f1×a1×S(t)/N。人群转换关系如图1 所示。
通过以上分析可以得出SEIR 的数学模型:

该模型中参数a1、a2、f1、f2和d 在疫情发展的各个阶段受实际因素影响会有比较明显的变化,现分析如下:

图1 SEIR 模型框图
(1)参数a1、a2表示单位时间内1 名传染者与他人的接触感染概率。该参数与全社会的警觉程度和政府、公众采取的各种措施有关,例如:佩戴口罩、减少停留在公共场所的时间、喷洒消毒药剂、提高隔离强度等都能有效地降低接触感染概率[9-10]。
(3)参数d 为确诊人群单位时间内康复的概率,疫情传播初期没有特效药与针对性的治疗方法,康复率比较低;随着疫情阶段的发展,相关药物研制推出,康复概率大幅上升[11]。
2 基于WPF 方法的仿真实现
2.1 疫情数据存储与可视化
2.1.1 数据存储
本模型使用MySQL 8.0.14 数据库完成存储工作。MySQL 数据库存储了全国各省市疫情数据,存储表字段见表1。

表1 新型冠状病毒感染数据表字段
读取数据库相关数据的代码如下:


2.1.2 数据可视化
根据2020年1月27 日至2月28 日国家卫生健康委员会公布的湖北省新冠肺炎感染人数,由WPF 中chart 图表控件分别展示现有感染人数、治愈人数、死亡人数、日死亡率和日治愈率趋势曲线图(如图2~4 所示)。
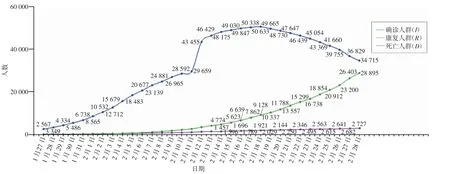
图2 湖北省新冠肺炎感染人数
从图2 中可以得出,2月18 日现存确诊人数为50 633 人,达到峰值,在此之后现存确诊人数开始下降,由于潜伏期人群的存在,可以估算2月16 日f1、f2达到最低值0,由此确定2月16 日以后为衰退期。根据疫情暴发规律的4 个时期,可以把1月27 日之前定为征兆期,1月28 日到2月6 日定为暴发期,2月7 日到2月15 日定为高峰期。
渔业养殖。推广稻田养鱼技术,科学规划,开挖鱼沟、鱼凼,放养鱼苗,主要包括鲤鱼、鲫鱼、辅以少量白鲢,开挖面积达到田块总面积的10%左右。
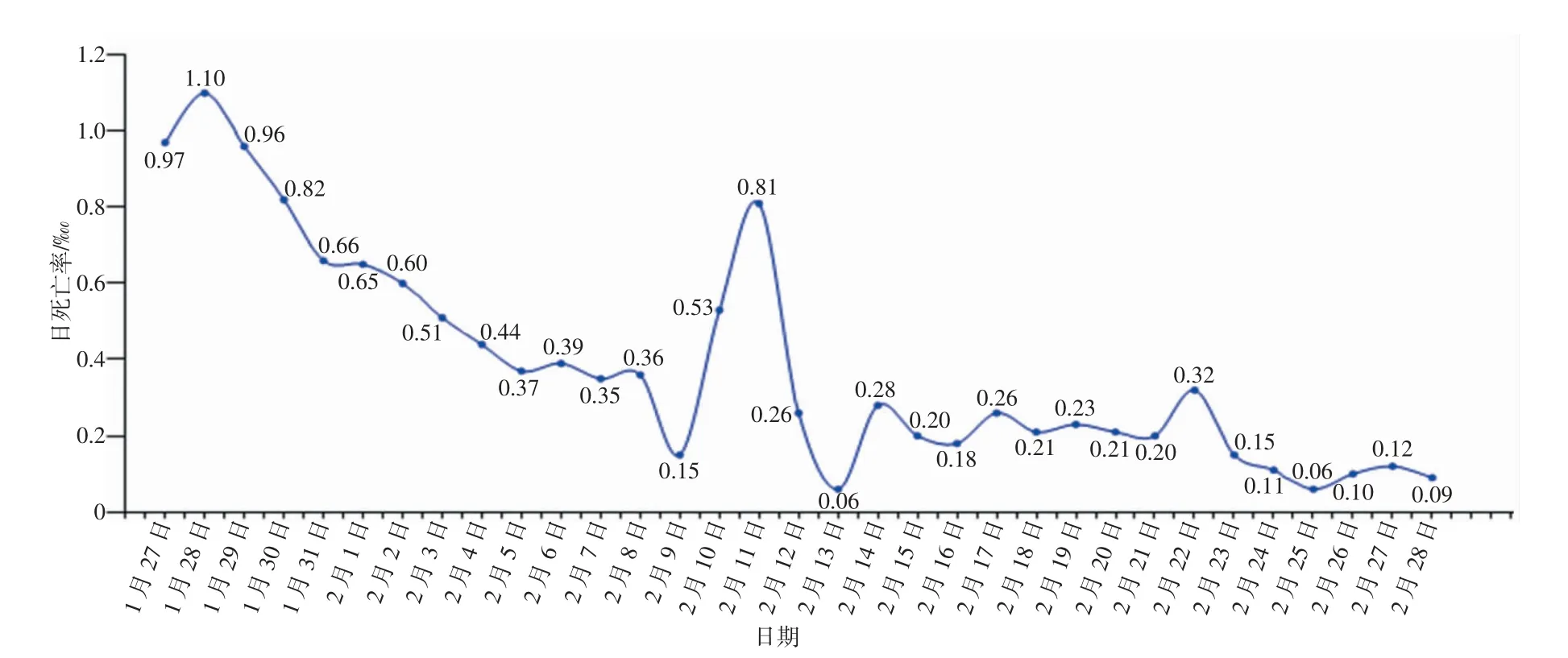
图3 湖北省新冠肺炎日死亡率

图4 湖北省新冠肺炎日治愈率
根据划分的4 个阶段,可以分阶段拟合计算日死亡率(fn)和日治愈率(dn),计算公式:fn=(Dn-Dn-1)/In,dn=(Rn-Rn-1)/In。由图3、4 可以看出,随着疫情发展日死亡率不断降低,日治愈率不断上升。
2.2 仿真模型算法实现
由SEIR 微分方程可以推导出如下关系:

SEIR 微分方程是由WPF 编程实现的,程序中S、E、I、R、D 的数值与前一天的数值是递推关系,可以通过多次调用private void Button_Click(object sender,RoutedEventArgs e)函数来实现计算,每次计算结果都通过图表chartAttMed1 显示出来。WPF 编程实现如下:

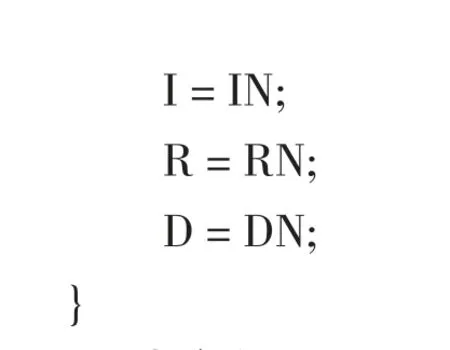
2.3 仿真参数分析
(1)征兆期。第一阶段是征兆期,主要发生在传染病初期,感染者临床症状表现不明显,在这个阶段病毒已经传播开了,但是并不能引起公众和政府的注意。由于携带病毒的传染源没有得到控制,所以这个时候感染率比较高、传播周期较长,但整个社会的发病率还比较低。潜伏期人群有2~14 d 的潜伏期,取平均值在8 d 后才会显现出来,c=1/8。征兆期死亡人数和治愈人数较少,因此忽略死亡人数和治愈人数,模型简化为

1月27 日湖北省新增新冠肺炎病例1 291 例,由此得出
根据钟南山院士对疫情预测数据,取a1=0.052 49,a2=0.052 49(95%置信区间0.050 68~0.054 29)[12]。
(2)暴发期。随着感染者不断增加,公众恐慌情绪增加,政府虽然采取多种防控措施,但对病毒传播的特点不清楚,没有收到预期效果,疫情进入暴发期。在这个时期,传播源的平均传播期依然较长,整个社会的潜伏期人员和确诊人员不断增加。暴发期内的潜伏期人员传播率(f1×a1)和确诊人员传播率(f2×a2)还维持一个高水平,确诊人员得到一些医疗救治,死亡率fn平稳线性降低,治愈率dn平稳线性上升;b 为潜伏期人群自我恢复的概率,为固定值。
第n 天参数值为

根据实际疫情数据可以大致估算出各参数值为:fn=(1.139 3-0.078 4×n)/100,dn=(0.747 3+0.015 9×n)/100,c=1/8,b=0.057,N=50 000 000,a1=0.052 49,a2=0.052 49,f1=4,f2=2。
(3)高峰期。当高强度的措施实施后,病毒扩散速度已经减慢,发病人数保持稳定,处在一个高平台防疫阶段。在这个时期,由于采取了有效隔离措施,降低了接触感染的概率,但由于病患基数较大,社会发病率依然很高。高峰期由于没有有效的治疗措施,所以死亡率f 维持在一个高水平,但轻度患者能及时恢复,治愈率d 因此有所提升。
同理取fn=(0.629 3-0.018 7×n)/100,dn=(0.815 7+0.055 7×n)/100,b=0.03,N=50 000 000,a1=0.052 49,a2=0.052 49。
2月12 日湖北省的病例诊断分类中增加了“临床诊断”,以便患者能及早接受规范治疗,对新就诊患者按照新的诊断分类进行诊断,进一步提高了救治成功率。因此2月12 日c 值明显提高,大幅减少了潜伏期人群数量,这里假设c=0.35;2月12 日以后假设所有的确诊人员都被收治,不再具有传染性,取f2=0。
2月7 日到2月11 日各参数值为:f1=3,f2=1,c=1/8。
2月12 日各参数值为:f1=3,f2=0,c=0.35。
2月13 日到2月15 日各参数值为:f1=3,f2=0,c=1/8。
(4)衰退期。在高平台现象持续一段时间以后,控制措施的作用开始显现,患病人数开始下降,进入衰退期。在这个时期,平均感染率最低,确诊人数增长出现拐点。衰退期各参数值为:fn=(0.532 2-0.011 3×n)/100,dn=(-7.835+0.453 7×n)/100,c=1/8,b=0.057,N=50 000 000,a1=0.052 49,a2=0.052 49,f1=0,f2=0。
3 仿真结果
将4 个阶段的参数输入仿真模型得到的仿真结果如图5 所示。由图5 可以看出,此仿真模型是参照现有疫情数据将疫情划分为不同阶段,分别建模计算参数。4 个阶段主要根据潜伏期人群增长率拐点划分,可以看出防护措施对潜伏期人群作用明显,但滞后作用于确诊人群。征兆期内潜伏期人群数量较少,增长率较高;随着防控的加强,潜伏期人群增长率降低,但是由于基数较大,潜伏期人群数量明显增加,进入暴发期;高峰期潜伏期人群增长率接近为0,数量维持在高位;衰退期潜伏期人群呈现负增长,数量急剧下降。由于潜伏期人群潜伏期为2~14 d,确诊人群数量变化滞后于潜伏期人群,影响潜伏期人群增长率的主要参数为f1、f2;疫情进入衰退期后f1=0、f2=0,确诊人数I 主要受康复的概率d 影响,提高康复率有助于缩短疫情周期。
根据仿真模型相关参数,可以推算出2月29 日到3月4 日现有确诊人数、死亡人数、治愈人数的数量,如图6 所示。从总体上看确诊人数依次递减,累计死亡和累计治愈人数依次递增,符合目前疫情真实趋势。仿真数据与真实数据对比情况见表2~4。
仿真模型通过存入数据库的疫情数据信息计算出最新的参数信息,再由WPF 编程实现迭代计算,通过WPF 中chart 控件呈现出预测的短期数据和长期走势图。从表2~4 中可以看出,现有确诊人数误差率在3%以内,平均误差为-1.04%;治愈人数误差率在3%以内,平均误差为-0.8%;死亡人数误差率在3%以内,平均误差为0.88%。综上,本仿真模型对未来5 d 的预测数据与真实数据吻合度较高,整体误差率在3%以内。

图5 湖北省新冠肺炎感染仿真图

图6 湖北省新冠肺炎感染人数预测

表2 现有确诊人数仿真数据与真实数据对比

表3 治愈人数仿真数据与真实数据对比
4 结论

表4 死亡人数仿真数据与真实数据对比
本文通过对传染病传播过程的分析,结合SEIR模型,通过WPF 编程仿真实现了对传染病传播趋势的预测。SEIR 模型在SIR 基础上引入了潜伏期人群,并考虑到潜伏期人群的潜伏期和传染性,根据潜伏期人群数量增长率划分了4 个阶段,然后分阶段编程计算参数信息,最终实现了新冠肺炎传播过程模拟仿真。通过对仿真结果定性、定量的分析,揭示了新冠肺炎传播的规律、变化趋势。初步结果表明:SEIR 模型仿真短期预测确诊人数、治愈人数和死亡人数的误差率在3%以内,并能根据现有参数信息仿真出未来长期走势图;疫情暴发征兆期、暴发期、高峰期确诊人数主要受到潜伏期人群数量影响,衰退期周期主要受到治愈人群康复率影响。该仿真模型可以为突发公共卫生事件防护工作中疫情分析、疫情研判、应急预案提供辅助决策支持。但该仿真模型并未对a1、a2、b、f1、f2进行动态分析,只是采用阶段性均值处理,对于疫情传播的征兆期、暴发期以及未来趋势预测的影响有待进一步研究。

