不同介电常数模型的平静海表面亮温仿真差异性分析

吴义生，韩震，2，3，周玮辰，王艺晴，劳国栋

(1.上海海洋大学 海洋科学学院，上海 201306；2.国家远洋渔业工程技术研究中心，上海 201306；3.上海河口海洋测绘工程技术研究中心，上海 201306)

0 引言

海洋盐度是认识和揭示海洋现象的基本物理参量之一，是研究温盐环流、海气相互作用和全球气候变化的重要依据[1]。走航观测与浮标观测等传统技术手段获取的海洋盐度数据时空分辨率不能满足海洋盐度业务化需求。为解决海洋盐度遥感数据严重不足的问题，2009年欧洲航天局ESA(European Space Agency)发射了SMOS卫星(soil moisture and ocean salinity)[2]，2011年美国航天局NASA(National Aeronautics and Space Agency)发射了“宝瓶座(aquarius)”卫星[3]，并且在2015年年初NASA发射了搭载L波段(1.4～1.427 GHz)辐射计的SMAP(soil moisture active and passive)卫星[4]。

卫星被动微波遥感通常利用L波段观测海表面盐度。在理想情况下，水平极化亮温对盐度的灵敏度为0.2～0.6 K/psu，垂直极化亮温对盐度的灵敏度为0.35～0.8 K/psu[5]。介电常数模型是电磁波频率、海表盐度和海水温度的函数，许多学者开展了海水复介电常数模型研究。早在20世纪90年代，Kelin和 Swift[6]利用在频率为1.43 GHz和2.653 GHz上获取的不同温度、盐度数据，拟合出Debye方程中各项参数，建立了经典的K-S模型，该模型适用于较低的微波波段频率。Blanch等[7]2003年根据电磁波信号传播方法，利用标准矩形波导，提出一个静态结构模型(Bl模型)，模型测试环境为1.43 GHz，盐度范围为0～40 psu。现在常用的介电常数模型还有Meissner-Wentz介电常数模型(简称M-W模型)[8-9]，该介电常数模型是基于双Debye方程，适用于较高的微波频率。

在前人的研究中，很少有学者专门进行不同介电常数模型仿真平静海表面亮温的分析。在本次研究中，使用Matlab R2016a软件，通过改变不同的输入参数的S函数，对K-S模型、Bl模型和M-W模型这3种介电常数模型进行了建模仿真，分析了介电常数实部、虚部值的差异性；计算了3种介电常数模型得到的平静海表面亮温和盐度变化率的关系，以及不同入射角对亮温的影响。

1 介电常数模型仿真分析

1.1 K-S模型仿真分析

在20世纪70年代，Ho和Hall利用NaCl溶液和海水在L和S波段进行实验，但是Klein & Swift对前者的数据统计分析，发现Ho等人测量的介电常数存在偏差，因此提出K-S模型[6]，其公式(1)为：

(1)

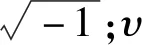
εs(T，S)=εs(T)a(S，T)

(2)

εs=87.134-1.949×10-1T-1.276×
10-2T2+2.491×10-4T3

(3)

a(S，T)=1+1.613×10-5ST-3.656×
10-3S+3.210×10-5S2-4.232×10-7S3

(4)

式中：S、T分别为实验数据的盐度、温度。

K-S模型在频率为1.43 GHz和2.65 GHz条件下进行实验得出静态介电常数、弛豫时间、离子电导率，假定η为0，则该模型中亮温的精度达到0.3 K，且盐度在4～35 psu(practical salinity units)的范围内效果较好。K-S模型是基于单一的Debye方程，对K-S模型进行仿真分析海水介电常数的实部与虚部，根据模型的特性，分析实部和虚部随电磁波频率与温度之间的关系，本次研究设定盐度为全球通用的盐度值32.54 psu，结果如图1 所示。

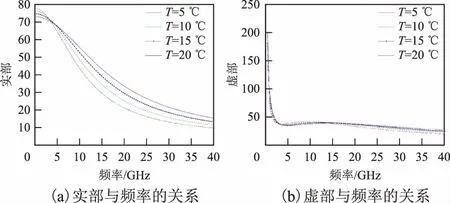
图1 不同温度下K-S模型介电常数与电磁波频率的关系

从图1(a)中可以看出，在不同的温度下，海水介电常数的实部随电磁波频率的变化。在频率为0～4 GHz之间，海水温度越低，介电常数实部值越高，在4～40 GHz的频段，实部值随着温度的升高有上升的趋势；从图1(b)中可以看出，对于介电常数虚部，在0～4 GHz频段，虚部随频率变化率很高，说明电磁波能量衰减率高。总体来看，介电常数实部值随着入射电场频率升高而减小，虚部在0～4 GHz频段随着频率升高快速减小，在4～40 GHz的频段，随着频率升高虚部值逐渐增加，变化比较缓慢，最终基本处于稳定的趋势，说明电磁波能量衰减很缓慢。

1.2 M-W模型仿真分析

Meissner和Wentz[8-9]提出的M-W模型是使用双Debye方程来拟合海水介电常数模型，模型如公式(5)所示：

(5)

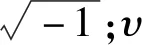
εs(T，S)=εs(T，S=0)·exp[b0S+b1S2+b2TS]

(6)

(7)

式中：b0、b1、b2为拟合系数。

对M-W模型进行仿真分析海水介电常数的实部与虚部，模型仿真条件同样设定盐度为全球通用的盐度值32.54 psu，得出的结果如图2所示。

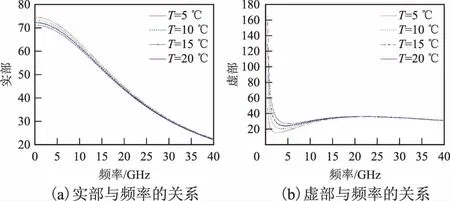
图2 不同温度下M-W模型介电常数与电磁波频率的关系

从图2(a)可以看出，由M-W模型得出的海水介电常数实部值随着入射频率的升高而降低，在0～4 GHz的频段下降得较缓慢，在4～40 GHz的频段下降速率变大；从图2(b)中可以发现，虚部值是在0～4 GHz频段下降速率很高，在4～40 GHz频段有增加的趋势并且逐渐趋于稳定状态，即在0～4 GHz频段电磁波能量随着入射频率变高衰减快，在4～40 GHz频段能量衰减很缓慢；M-W模型介电常数实部在0～4 GHz频段随着温度的升高有下降的趋势，随着频率升高，不同温度的海水实部值基本上无差异，同时虚部表现的也是在0～4 GHz频段差异较明显，且海水温度越高，衰减值越高。

1.3 Bl模型仿真分析

Blanch和Aguasca实验条件是测量频率为1.43 GHz，盐度范围为0～40 psu，低盐度间隔为2 psu，高盐度间隔为1 psu，温度变化从0～40 ℃，间隔为0.7 ℃，通过对该条件下的数据进行拟合，得出Bl模型。Bl模型同样也是基于单一的Debye方程，只是获取静态介电常数、弛豫时间和离子电导率的方法有差异，模型的形式如(8)所示[10]：

(8)

式中：ε∞值为4.9；εs为静态介电常数，跟温度和盐度有关；Bl模型实验数据拟合出相关系数；ε0为真空中的电容率，数值为8.854*1e-12；τ为弛豫时间，其中Bl模型的静态介电常数[7]形式如下：

εs(T，S)=εs(T)c(S，T)

(9)

εs=87.346-3.436×10-1T-1.912×
10-3T2+3.812×10-5T3

(10)

c(S，T)=1+1.552×10-5TS-3.970 3×
10-3S+3.059 6×10-5S2

(11)

式中：S、T分别为实验盐度、温度。

对Bl模型进行仿真分析海水介电常数的实部与虚部，模型仿真条件同样设定盐度为全球通用的盐度值32.54 psu，得出的结果如图3所示。

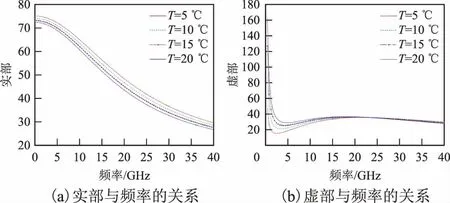
图3 不同温度下Bl模型介电常数与电磁波频率的关系

从图3(a)中可以看出，由Bl模型得出的海水介电常数实部值随着入射频率的升高而降低，在0～4 GHz频段下降得较缓慢；从图3(b)中可以看出，对于介电常数虚部，在0～4 GHz频段，虚部值随频率变化率很高，此时电磁波能量衰减率高，在4～40 GHz频段有增加的趋势并且逐渐趋于稳定状态；Bl模型介电常数实部值在0～4 GHz频段随着温度的升高有下降的趋势，而且下降的值几乎是等间隔的，虚部表现出在0～4 GHz频段差异较明显，且海水温度越高，衰减值越高，但是在4～40 GHz频段随着频率升高，海水温度对虚部值几乎没影响，即电磁波能量衰减程度是一样的。

1.4 3种模型不同入射频率的差异性分析

3种模型的实部值、虚部值与入射频率密切相关。本文计算了盐度为全球通用平均盐度32.54 psu和海水表面温度为平均海水温度17.4 ℃的情况下[11]，3种模型实部、虚部值随不同入射频率的变化(图4)。

图4 3种介电常数实部和虚部与入射频率的关系

从图4(a)可以看出，在0～4 GHz低频段，K-S模型得出的介电常数实部值相对于其他2个模型是较大的，在之后的较高频段M-W模型的值是最高的，且K-S模型的值变为三者中最小的；从图4(b)中可以看出，对于虚部，由于盐度遥感所选用的是L波段(1.4～1.427 GHz)，所以重点比较3种模型在这个频段内的差异，但是从4(b)可以看出，在1～2 GHz频段内，K-S模型的衰减量更大，而M-W模型和Bl模型衰减值基本上是一致的；总体上3种模型的介电常数实部随着频率的升高，实部值逐渐减小，虚部在0～4 GHz是快速降低，接着逐渐升高，最后趋于稳定。3种模型介电常数总体趋势是相同的，但是也存在着差异，产生这些差异最主要的是由于静态介电常数方程的建立不同。

2 平静海表面亮温建模仿真

根据普朗克黑体辐射定律，定义物体的亮度温度(亮温)为与物体具有相同辐射功率的黑体的温度，因此亮温可以用来表征物体的微波辐射能量[12]，微波波段的平静海面亮温TB与海表物理温度SST有如下的关系：

TB=e(θ)·SST

(12)

式中：e(θ)为海面发射系数；SST为海表温度，根据基尔霍夫定律，发射系数与反射系数存在如下的关系：

e(θ，φ)+Γ(θ，φ，ε)=1

(13)

式中：Γ为菲涅尔反射系数，是入射角θ、海水介电常数ε、方位角φ、极化方式P的函数，在水平(h)和垂直(v)极化条件下，反射系数分别为：

(14)

(15)

式中：ε为海水介电常数，可以由介电常数模型计算。

为了分析不同介电常数模型在不同入射角下，根据盐度卫星入射角的规律[13-14]，本文将入射角θ分别设定为15°、35°和55° 3种情况，在此基础上分析了不同模型平静海面亮温对盐度的灵敏度的差异性。图5温度设定为17.4 ℃时，3种模型在频率为1.413 GHz的水平极化亮温(Th)、垂直极化亮温(Tv)。

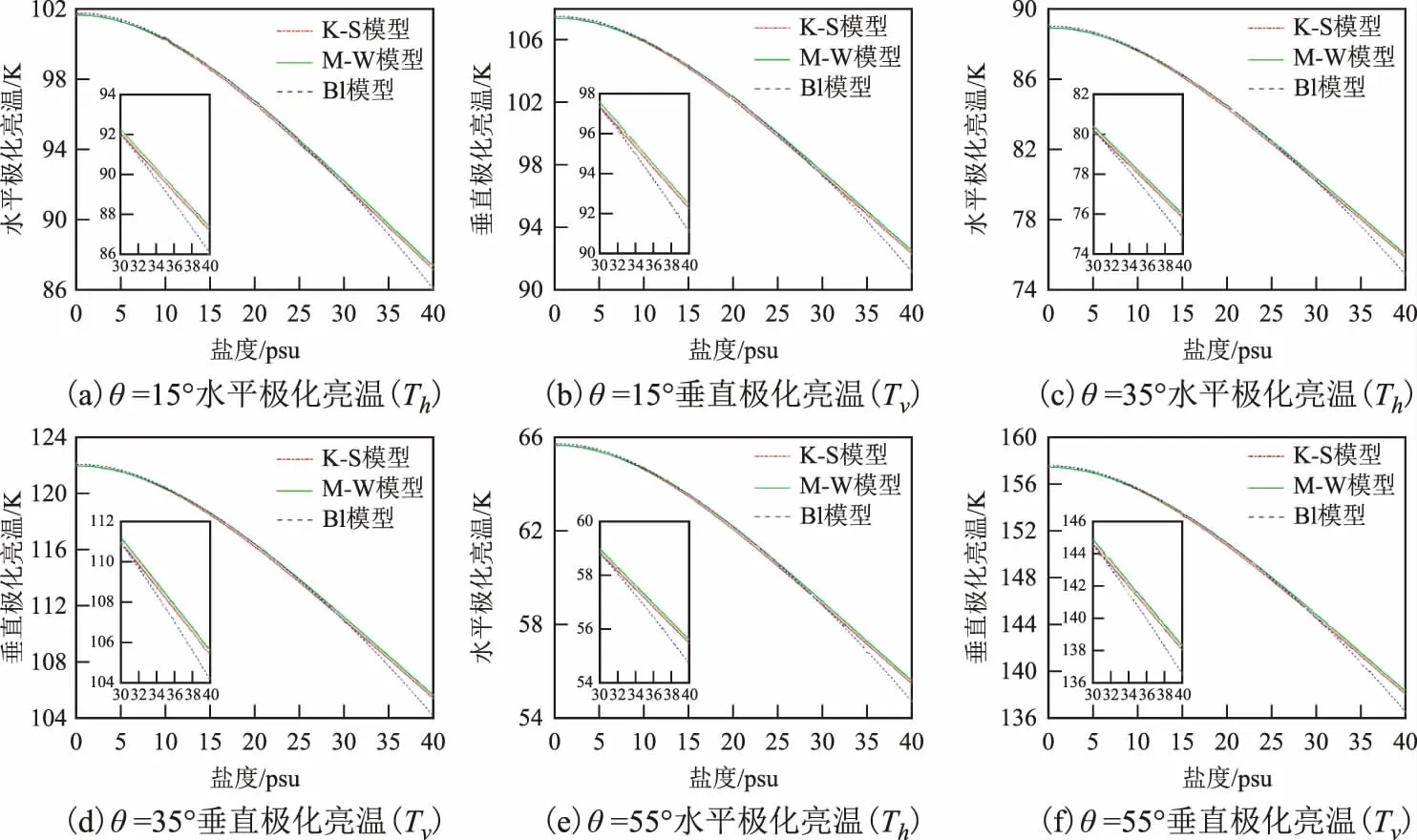
图5 不同介电常数模型在不同入射角的情况下的亮温和盐度的关系

从图5可以看出，电磁波入射角越大，水平极化亮温值越低，而垂直极化亮温值是随着入射角的增大而升高；对于平静海面亮温，盐度与亮温的关系是随着盐度的升高，水平极化和垂直极化亮温值逐渐降低；3种模型下亮温和盐度关系的差异主要是由于模型中变量参数环境不同造成的。由于全球开放海域的盐度值一般大于32 psu，所以为了更直观地体现3种模型亮温与盐度的关系，重点关注盐度区间为30～40 psu，变化率用如下公式计算：

(16)

式中：T30、T40分别代表盐度为30 psu、40 psu的极化亮温;S30、S40分别代表盐度为30 psu、40 psu；P为极化方式。表1是盐度范围为30～40 psu的条件下，3种模型不同极化方式下亮温和盐度的关系。

表1 不同模型和极化方式下亮温与盐度变化率的关系 K·psu-1

注：Th_variance、Tv_variance分别为水平极化亮温、垂直极化亮温与盐度的变化率。

从表1中可以看出，在同一介电常数模型下，垂直极化亮温与盐度的变化率高于水平极化亮温与盐度的变化率，在入射角为15°时，亮温与盐度的变化率基本不受亮温的极化方式影响；在入射角为55°时，亮温与盐度的变化率受亮温的极化方式影响最大，3种介电常数模型的水平极化亮温与盐度的变化率分别为0.307 8 K/psu、0.310 1 K/psu、0.382 5 K/psu，垂直极化亮温对盐度的变化率分别为0.603 1 K/psu、0.604 6 K/psu、0.748 8 K/psu，3种模型的垂直极化亮温与盐度的变化率比水平极化亮温与盐度的变化率高30%左右；随着电磁波入射角的增大，水平极化亮温与盐度的变化率是逐渐降低的，垂直极化亮温与盐度的变化率是逐渐升高的；在同一入射角的情况下，K-S模型和M-W模型的极化亮温与盐度的变化率大致相同，而Bl模型的极化亮温与盐度的变化率要高于前二者模型。

基于微波遥感理论反演海表面盐度的主要影响要素分别为：海表面亮温、海表面温度、微波辐射计的入射角和工作频率。海表面亮温是反演海表面盐度的关键，3种模型的平静海面亮温存在一定的差异，对其差异性进行分析对于提高海表面盐度遥感反演精度具有重要的指导意义。3种模型平静海面亮温的差异产生的原因主要是因为三者的实验频率、温度和盐度不完全相同(表2)。K-S模型适合海水盐度在4～35 psu的情况下，1.43 GHz和2.653 GHz频率的微波遥感探测；Bl模型适合海水盐度在0～40 psu的情况下，低频微波遥感探测，在同样海水盐度范围内；M-W模型适用的电磁波频率范围更广。

表2 3种介电常数模型主要实验条件

3 不同入射角和亮温关系

由上述分析可知，极化亮温与入射角有关。本文计算了海水盐度为32.54 psu和温度17.4 ℃的情况下，3种模型平静海面极化亮温与入射角的关系(图6)。

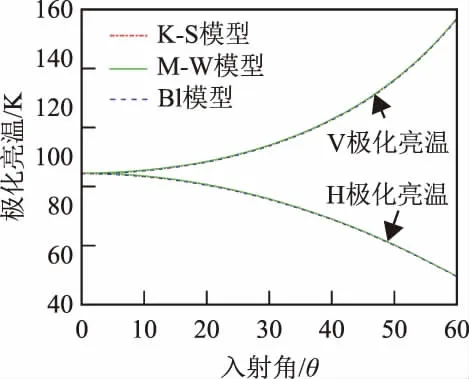
图6 平静海面极化亮温与入射角关系

从图6中可以看出，3种模型得到的垂直极化亮温随着入射角的增大而升高，而水平极化亮温随着入射角的增大而降低，而且相同的入射角，垂直极化亮温的值是高于水平极化亮温的，但是在入射角为0°的情况下，2种亮温值是相同的。此外，本文还取3种模型极化亮温的平均值作为参考值，计算了其绝对偏差值(图7)。

绝对偏差值=观测值-平均值

(17)

式中：观测值为3种模型的亮温值；平均值为3种模型的平均亮温。

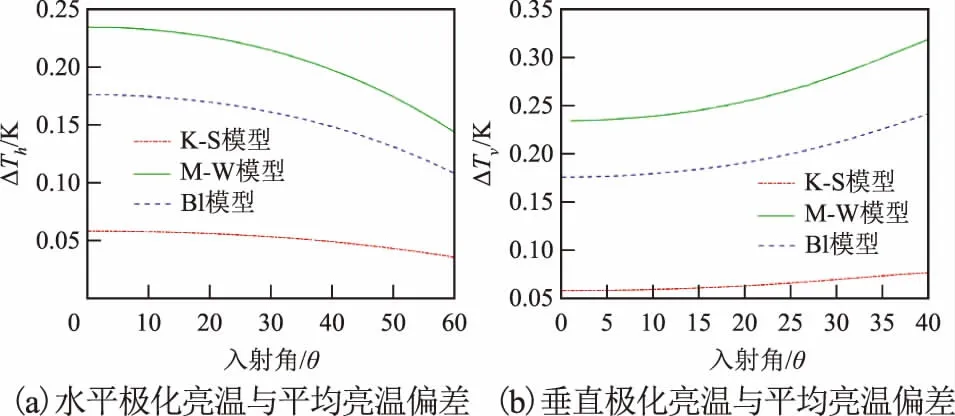
图7 3种模型极化亮温与平均亮温偏差曲线

从图7可以看出，水平极化亮温偏差随着入射角的增大而减小，垂直极化亮温随着入射角的增大而增大，K-S模型亮温偏差是最小的，M-W模型偏差是最大的，即K-S模型得出的亮温值最接近3种模型的亮温均值。3种模型的差异主要是由于三者的静态介电常数、弛豫时间设置是不一样的，以及模型实验数据是在不同条件下获得的，因此实验所获得的拟合系数有着较大的差别，导致其亮温值存在差异。

4 结束语

不同介电常数模型进行平静海表面亮温仿真具有差异性。本文利用Matlab软件对K-S模型、M-W模型和Bl模型3种介电常数模型进行平静海表面亮温了仿真分析，得出的主要结论有：

①在0～4 GHz频段范围，K-S模型介电常数实部值高于其他2个模型；在4～40 GHz频段范围，M-W模型的介电常数实部值最高，K-S模型的介电常数实部值最小。在虚部，3种模型的变化基本一致，在L波段(1.4～1.427 GHz)，K-S模型的衰减最强，而M-W模型和Bl模型衰减程度值基本一致。

②在进行海表面盐度遥感时，海水盐度在0～40 psu的情况下，Bl模型适合低频微波遥感探测，M-W模型适用的电磁波频率范围更广，K-S模型适合海水盐度在4～35 psu的情况下，低频微波遥感探测。

③在入射角为55°时，亮温与盐度的变化率最大；随着电磁波入射角的增大，水平极化亮温与盐度的变化率逐渐降低，垂直极化亮温与盐度的变化率逐渐升高；在同一入射角的情况下，K-S模型和M-W模型的亮温与盐度的变化率大致相同，Bl模型的亮温与盐度变化率要高于前二者模型。

④电磁波入射角越大，水平极化亮温越低，而垂直极化亮温是随着入射角的增大而升高，K-S模型亮温偏差最小，M-W模型偏差最大。