基于DRGAN和支持向量机的合成孔径雷达图像目标识别

徐 英，谷 雨，彭冬亮，刘 俊

(杭州电子科技大学 自动化学院，浙江 杭州 310018)

1 引 言

合成孔径雷达(Synthetic Aperture Radar， SAR)图像自动目标识别(Automatic Target Recognition， ATR)是SAR图像解译的一个重要研究方向，通过对SAR图像进行处理，实现对感兴趣目标的自动检测、鉴别与分类，是导弹末制导、海洋监视与矿藏探测等应用的重要环节之一[1]。

SAR传感器通常搭载在航空器和航天器等运动平台，利用合成孔径原理实现高分辨率微波成像，故SAR图像数据获取成本高。SAR图像具有目标方位角敏感性，在不同操作条件(成像参数)下SAR图像中目标外观差异大。SAR图像具有较强的相干斑噪声，严重影响目标的分割检测质量。虽然研究学者已经提出了很多SAR ATR算法，但这些算法通常在特定的操作条件下才能够取得理想的分类结果，距离成熟应用还有一段距离[2]。对于SAR ATR问题，在目标方位角不完备及成像参数变化较大情况下导致训练样本有限时，如何提高SAR图像的目标识别性能，是值得深入研究的一个重要问题[3]。

特征提取与选择、分类器优化设计是影响识别精度的两个关键要素[4]。目前用于SAR图像目标识别的典型分类器包括模板匹配、支持向量机(Support Vector Machine， SVM)[5]、稀疏表示[6]和集成学习[7]等。随着深度学习理论和技术的飞速发展，卷积神经网络(Convolution Neural Networks， CNN)作为一类典型的监督深度学习模型，在目标检测与识别方面取得了优于传统方法的成果，已经开始应用于SAR图像目标识别。在模型结构设计方面，文献[8]参照VGGNet结构，设计了一种用于SAR ATR的CNN结构，但由于采用较小的卷积核(3×3)，所以对MSTAR(Moving and Stationary Target Acquisition and Recognition)数据集中10类含变体目标的分类精度仅为93.16%。文献[9]提出的模型(A-ConvNets)使用了较大的卷积核(5×5，6×6)，且采用全局平均池化代替全连接层，由于减小了模型参数，故在数据增强的情况下对10类不含变体目标的分类精度能够达到99.13%。文献[10]通过实验分析了加性和连接特征融合结构对基于CNN的SAR图像识别性能的影响，并提出了一种基于多特征决策级融合的CNN模型结构(Fusion-CNN)，对10类不含变体目标的分类精度达到了99.42%。文献[11]研究了CNN模型中第一层，即空间特征提取层，对识别精度的影响，设计了一种基于多尺度空间特征提取的深度CNN结构(MultiScale-CNN)，对10类含变体目标的分类精度达到了97.69%。

将CNN用于SAR ATR时，为解决数据集中训练样本不足的问题，通常采用数据增强手段获得足够多的训练样本来提高模型的泛化能力。文献[3]提出了一种基于目标散射中心的SAR图像增强方法。文献[5]研究了仿射变换和弹性形变两种数据增强手段对SAR图像识别精度的影响。文献[8]采用平移、添加噪声和角度合成等操作获取增强后的训练样本集，实验结果表明这3种数据增强手段能极大提高模型的分类精度。文献[9]通过随机裁剪的方法，从分辨率为128×128的图像中提取分辨率为88×88的子图像。除数据增强手段外，采用深度生成模型生成样本也是一种有效增加样本数量的方法。为解决目标域SAR图像方位角缺失的问题，文献[12]首先采用光线追踪原理生成多种方位角下的SAR仿真图像。为提高仿真图像的质量，基于CycleGAN算法[13]将图像由仿真域转换到目标域，实现了目标域图像的数据增强。文献[14]提出了可旋转隐空间的思想，通过输入具有不同方位角的两幅SAR图像，采用编码器-解码器结构作为输入图像的隐空间特征表示，利用该特征学习得到一个旋转变换矩阵，然后利用学习得到的矩阵生成多种方位角下的SAR图像。文献[15]设计了基于深度生成神经网络的目标特征空间零样本学习模型，设计的模型包括构造器、生成器和解析器3个模块，其中构造器将输入的样本标签转换到目标特征空间，然后结合目标的方位角信息通过生成器重构目标图像。文献[16]通过改进Wasserstein自编码器模型结构和重构误差提高了SAR图像样本生成的质量。

考虑到SAR图像具有目标方位角敏感性，本文借鉴人脸识别领域提出的基于解耦表示学习的生成对抗网络模型 (Disentangled Representation Learning Generative Adversarial Networks， DRGAN)[17]，首先基于多尺度分形特征估计图像中的目标方位角，对其量化编码后，将训练样本和目标方位角编码向量等作为输入优化DRGAN模型参数。然后，将训练得到的DRGAN模型视为目标方位角估计器，将训练样本和测试样本归一化到同一方位角量化区间。最后，从变换后的图像中提取归一化灰度特征，采用SVM训练分类器。采用MSTAR数据集进行模型训练和目标识别实验，验证了提出算法的有效性。

2 基于DRGAN和SVM的SAR图像目标识别流程

本文提出的基于DRGAN和SVM的SAR图像目标识别算法总体框图如图1所示。

采用多尺度分形特征对SAR图像进行增强，对经过阈值分割后的二值图像基于Hu不变矩估计目标方位角。对估计的目标方位角进行量化编码；利用SAR训练图像及方位角编码向量对DRGAN模型进行参数优化；基于训练得到DRGAN模型中的深度生成模型对SAR训练图像进行方位角归一化，提取SAR图像灰度特征，训练SVM分类器；基于训练得到DRGAN模型中的深度生成模型对SAR测试图像进行方位角归一化，提取SAR图像灰度特征，利用训练得到的SVM分类器进行测试。

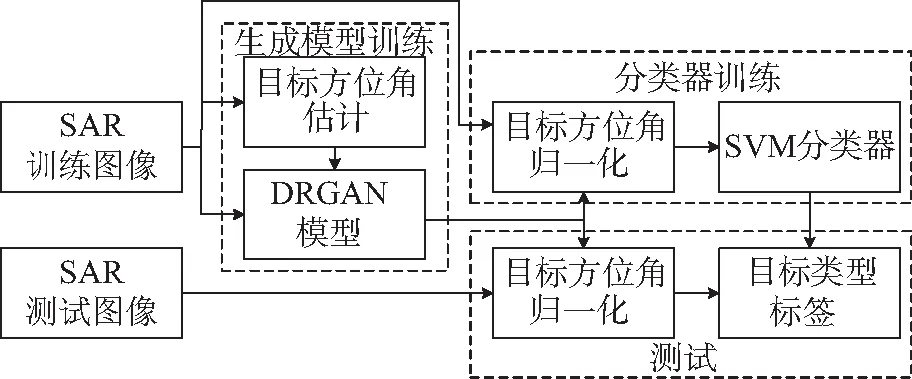
图1 本文算法流程框图Fig.1 Flowchart of proposed algorithm

3 算法实现细节

3.1 基于多尺度分形和Hu二阶矩的目标方位角估计

由于SAR图像具有较强的相干斑噪声，在计算多尺度特征进行图像增强前，首先采用5×5的滤波核对输入SAR图像进行均值滤波。

依据分形理论，利用地毯覆盖法在尺度ε=1，2，…，εmax的情况下计算二维图像表面积A(x，y，ε)的公式如式(1)和式(2)所示[18]：

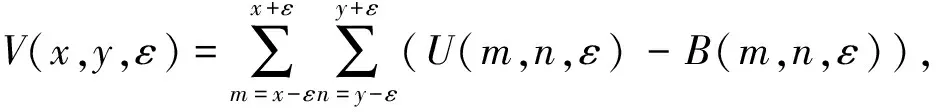
(1)

A(x，y，ε)=V(x，y，ε)/2ε，

(2)

其中，U(m，n，ε)和B(m，n，ε)分别为像素坐标x，y处，尺寸为(2ε+1)×(2ε+1)范围内像素的最大值和最小值，V(x，y，ε)为像素坐标x，y处由最大值和最小值曲面围成的三维空间的体积。

定义一个随尺度变化的分形特征K(x，y，ε)，其计算公式为[18]：

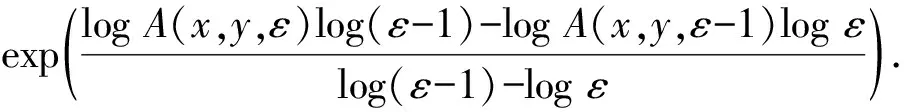
(3)

基于多尺度分形特征K(x，y，ε)定义一个度量IMFFK(x，y)用于图像增强，如式(4)所示：

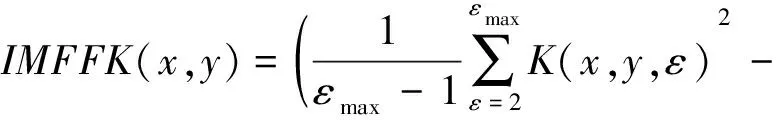
(4)

得到增强后图像采用自适应阈值分割算法得到目标检测结果，即目标二值图像。由于相干斑噪声的影响，分割后的图像中会有多个非连通区域。本文采用面积滤波法，计算目标二值图像中的每个连通区域的包围盒，然后选择面积最大的区域作为候选目标区域，基于Hu二阶矩估计目标的方位角[19]。估计得到目标方位角后，需要对其量化编码才能作为DRGAN模型中生成模型G的输入。本文将角度范围[0°， 360°)均分为Na个区间，每个区间的角度范围θ如式(5)所示。此时能够将目标方位角估计值转化为独热(one hot)编码形式a。

(5)

3.2 DRGAN模型设计与参数训练

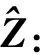
(6)

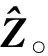
考虑到SAR图像样本数较少，本文在文献[17]设计模型基础上，将卷积操作的输出通道数减少为原来的一半，设计的判别模型D和生成模型G如表1所示。其中，Conv*表示Conv+BN+elu组合，DeConv*表示DeConv+BN+elu组合，Conv表示卷积操作，DeConv表示反卷积操作，BN表示批归一化操作，elu表示指数线性单元激活函数，详细见文献[17]。

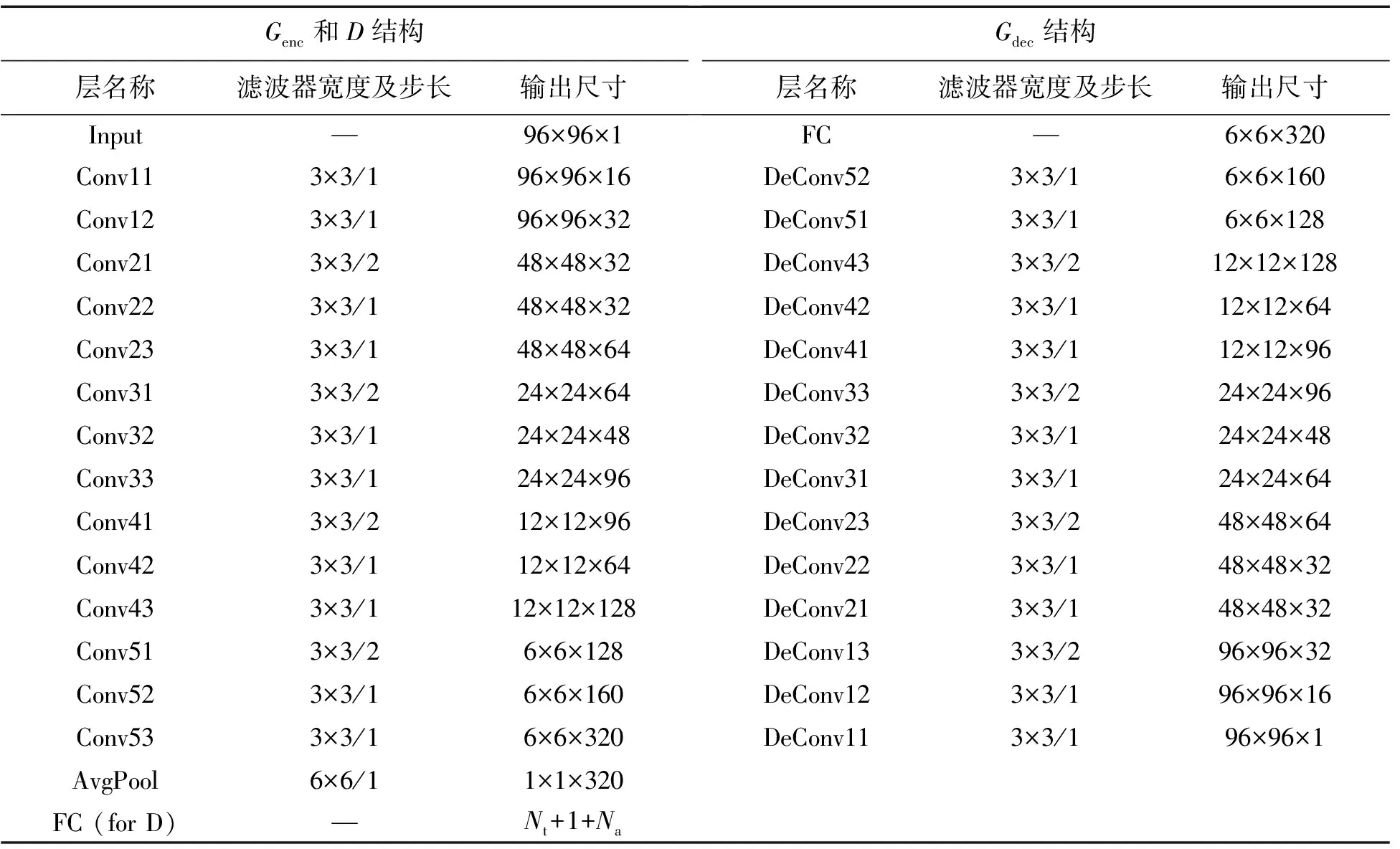
表1 DRGAN模型中判别模型D和生成模型G结构

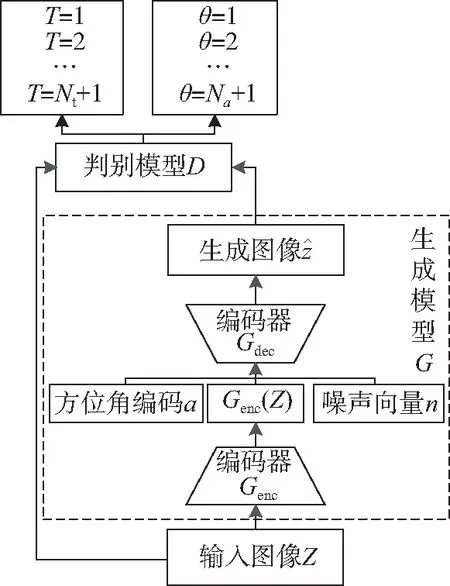
图2 DRGAN模型结构框图

Fig.2 Block diagram of DRGAN model

3.3 基于SVM的分类器设计

训练得到DRGAN模型后，一方面可以用于生成不同角度的训练样本，另一方面可以将不同角度的图像归一化到同一方位角区间。因为本文估计得到的目标方位角带有一定误差，且对其进行了量化处理，故采用第一种方法生成图像时与输入训练样本图像的分布会有一定差异，故本文采用后一方法对输入图像进行方位角归一化。

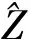
4 实验结果分析

为验证本文提出算法的有效性，采用MSTAR数据集在多个场景下进行算法测试，并与目前已知的算法分类结果进行对比分析。训练DRGAN模型时，输入SAR图像的分辨率为96×96。采用Adam优化器，学习率设定为0.000 2，批大小设定为32。目标方位角量化区间设为Na=30，随机噪声n维度设定为50。每训练完一次判别模型D，训练4次生成模型G。训练模型D采用的损失函数为交叉熵损失函数。SVM分类器采用径向基(rbf)核函数，gamma值设定为0.000 1，惩罚系数C设定为32，采用“一对多”的分类策略，迭代次数设定为1 000。

参考文献[8]，标准操作条件下MSTAR数据中10类训练样本和测试样本类别和数目见表2，将其记做SOC。本文对测试样本中包含变体和不包含变体情况分别进行了算法性能测试。此外，采用了文献[6]和文献[9]中使用的4种扩展操作条件测试提出算法的性能，分别记做EOC1-EOC4。EOC1和EOC2的配置见文献[9]，其中EOC1场景对2S1，BRDM2，ZSU234和T72 4类目标进行分类，用于比较在较大平台俯视角差异情况下的识别精度，EOC2主要用于测试型号不同情况下的目标识别能力。EOC3和EOC4的配置见文献[6]。在EOC3条件下，对BMP2，T72，BTR60和T62 4类目标进行分类，其中BMP2和T72存在变体情况，训练时采用SN9563和SN132型号，测试样本的型号分别为SN9566，SNC21，SN812，SNS7。EOC4主要测试分类器对于含变体情况的目标识别能力。与EOC1不同，EOC4仅采用2S1，BRDM2和ZSU234 3类目标，并没有采用T72。测试样本分别采用俯视角为30°和45°下的目标样本图像，其中BRDM2和ZSU234存在变体情况。本文仅测试俯视角为30°情况下的识别精度。

表2 MSTAR数据集描述

采用本文设计的DRGAN模型中的深度生成模型G对训练样本进行角度归一化后的图像如图3所示。其中，方位角a的one hot编码设定为[1， 0， …， 0]，随机噪声n设定为零向量。从图3可以看出，几乎所有的目标方位角均沿水平方向，仅图像的灰度分布有一定差异。方位角归一化后的SAR图像位于高维欧氏空间的若干低维流形，这将有利于后续分类器的设计。

图3 型号为2S1的方位角归一化SAR图像(前60个训练样本)

Fig.3 Aspect angle normalized SAR images for 2S1 class (first 60 training samples)

本文算法在SOC配置下进行目标识别的混淆矩阵、平均分类精度(Average Accuracy， AA)和总体分类精度(Overall Accuracy， OA)如表3所示，其中每一行最右边一列代表该类别的分类精度(Percentage of Correct Classification， PCC)。在测试样本包含变体的情况下总体分类精度达到97.97%，与目前基于深度CNN模型的方法接近。在4个扩展操作条件EOC1-EOC4条件下本文算法的识别结果分别如表4～表7所示。从表中可以看出，在扩展操作条件下，本文提出算法仍然取得了优异的分类性能，总体分类精度分别达到了97.83%，91.77%，97.11%，97.04%，平均分类精度分别达到了97.83%，91.77%，97.63%，97.19%。这说明了本文提出算法的适用性，在多种操作条件下均能取得较好的识别性能。

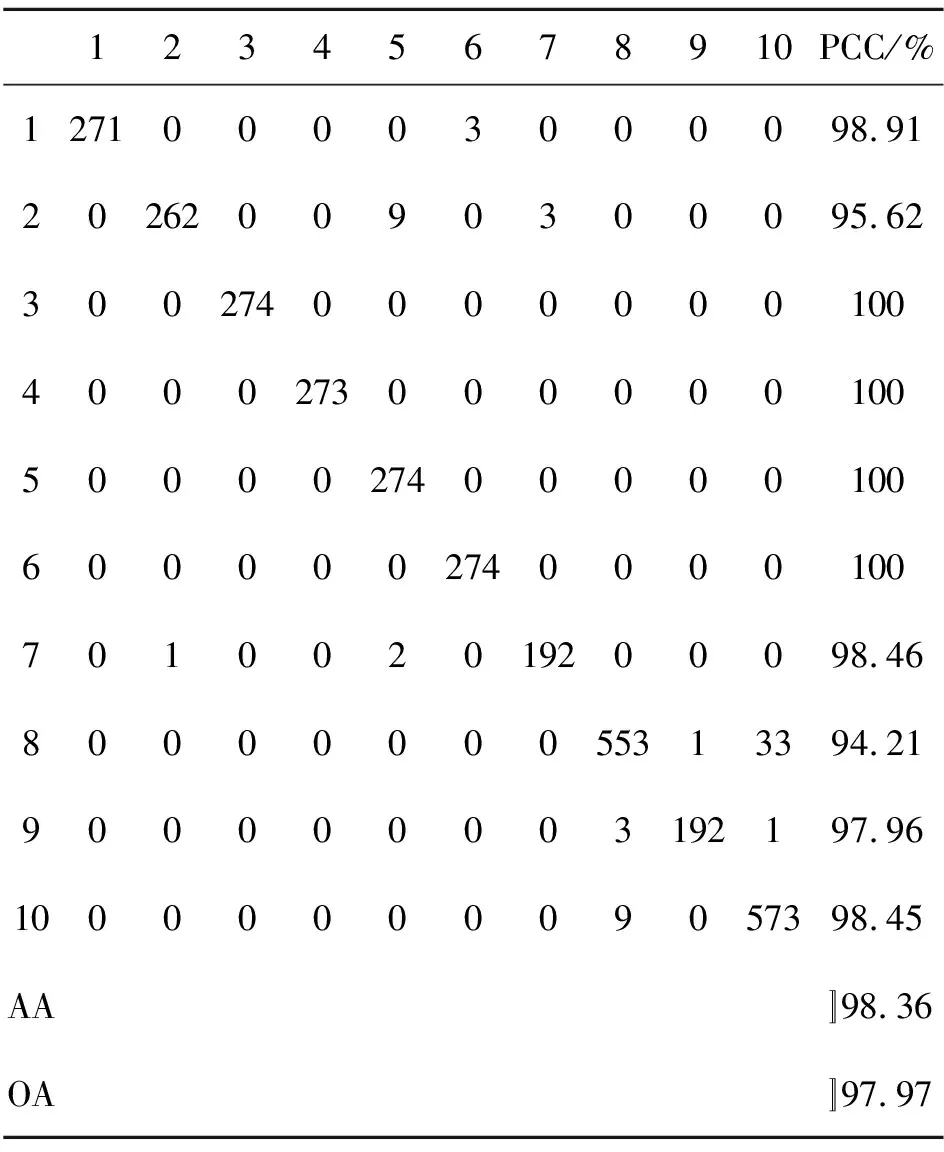
表3 标准操作条件下本文算法的混淆矩阵

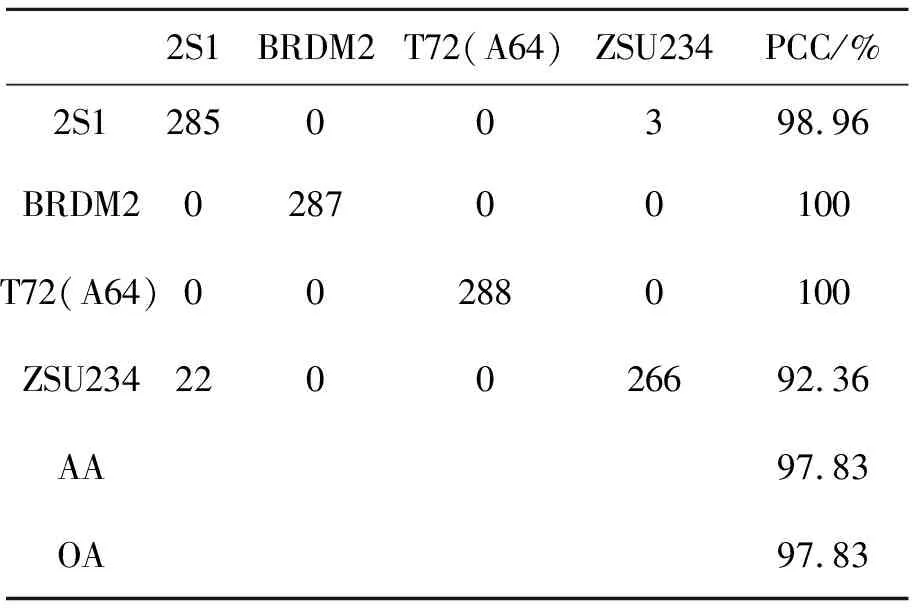
表4 EOC1下本文算法的混淆矩阵

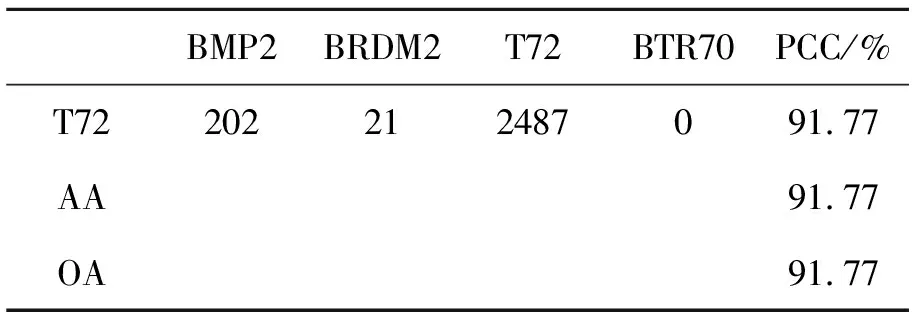
表5 EOC2下本文算法的混淆矩阵

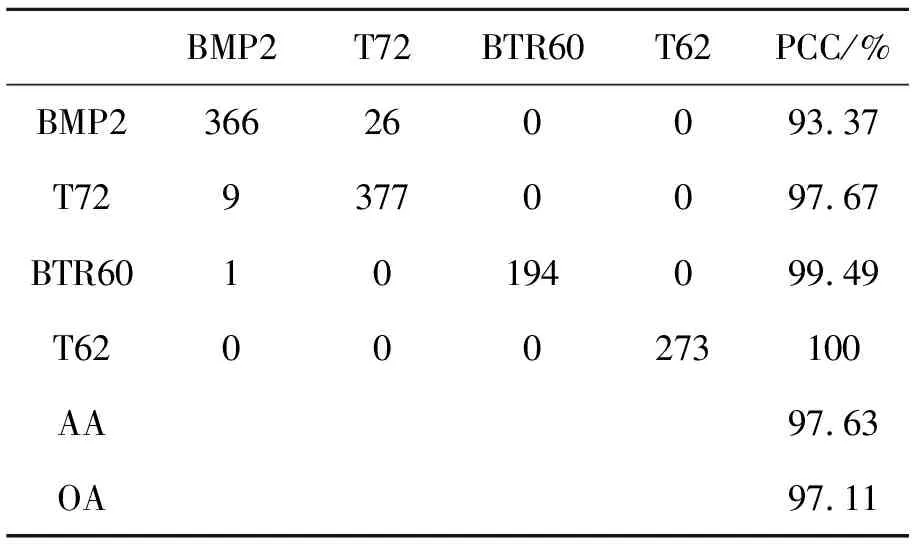
表6 EOC3下本文算法的混淆矩阵

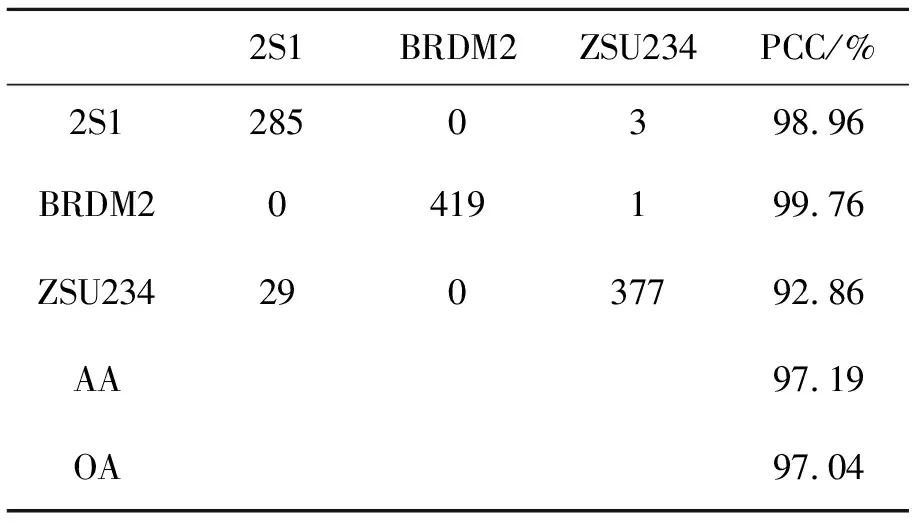
表7 EOC4下本文算法的混淆矩阵

本文算法与文献中提出算法在多种操作条件下的对比结果如表8所示。当采用表2中的训练样本进行训练时，本文提出算法的识别精度如表8中OURS所示。基于本文提出的目标方位角估计算法直接对SAR图像进行方位角归一化，然后提取灰度特征，利用SVM进行分类，该结果记做SVM+ROTATED。文献[5]采用经过预训练的CNN模型作为特征提取模块，基于SVM训练分类器。虽然文献[5]在SOC场景下取得了最优的分类精度，但是该算法需要已知目标的精确方位角信息对原始图像进行校正，同时采用了表2中的所有训练样本，且采用了更加有效的数据增强手段。

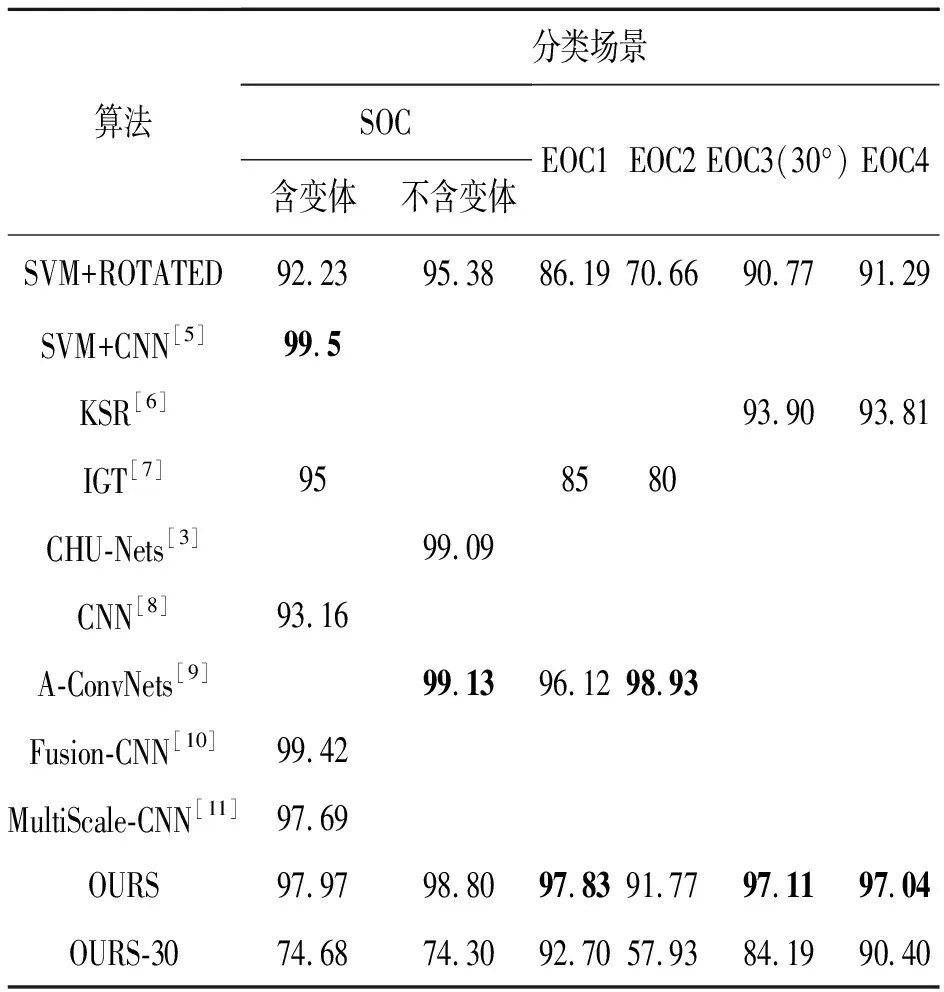
表8 多种操作条件下各算法的总体分类精度

从表8中可以看出，本文提出算法在多个扩展操作条件下取得了最高的识别精度，而直接利用估计的方位角对训练样本进行旋转的分类精度不高，故也验证了本文采用的基于DRGAN的深度生成模型进行方位角归一化的有效性。为验证DRGAN模型的目标方位角解耦学习能力，采用表2中每类训练样本的前30个样本训练DRGAN模型(注：MSTAR数据集中每60个样本使得目标方位角基本能够覆盖0°～360°)，并利用训练模型对这些训练样本和所有测试样本进行方位角归一化处理，目标识别结果如表8中OURS-30所示。从中可以看出，本文提出算法仅在EOC2的情况下识别精度不理想，在其他4种操作条件下，均取得了较高的识别精度。这主要是因为在EOC2场景下测试样本包含了T72的5个不同子型号(S7， A32， A62， A63， A64)，而训练样本的子型号与之不同(SN132)，当没有足够训练样本的情况下，深度生成模型对样本分布的学习不是很充分，导致识别精度较低。

与基于稀疏表示和基于深度CNN等主流SAR图像目标识别方法对比结果可以看出，本文提出算法优于或者接近多数经过数据增强训练得到的CNN模型的分类精度，要明显高于基于稀疏表示识别算法。

本文采用的DRGAN模型是一种深度生成模型，若能准确地估计SAR图像中的目标方位角，则可以利用该模型进行训练样本的增广，从而解决SAR图像识别中训练样本缺乏的问题，进而通过深度模型的优化设计提高SAR图像目标识别的准确率。

5 结 论

本文提出了一种结合DRGAN和SVM的SAR图像目标识别算法，采用MSTAR数据集在多种操作条件下验证了提出算法的有效性。由于SAR图像具有目标方位角敏感性，故采用DRGAN学习能够得到与方位无关的目标外观表示。虽然采用的目标方位角估计算法带有一定的误差，但通过设置较大的量化区间，能够削弱该估计误差对识别精度的影响。从变换后图像中提取特征，采用SVM进行分类器设计，能够取得与基于深度CNN模型相当的精度，这也验证了采用的深度生成模型的有效性。实验结果表明，本文提出算法在标准操作条件分别取得了97.97%和98.80%的识别精度，在扩展操作条件下分别取得了97.83%、91.77%、97.11%和97.04%的识别精度，能够在不进行复杂数据预处理的情况下，取得优异的识别正确率，能够满足SAR图像目标识别应用的需求。