空间机器人捕获航天器操作的避撞柔顺无源神经网络H∞控制

艾海平，陈 力

(福州大学 机械工程及自动化学院，福建 福州 350116)

1 引 言

近年来随着空间技术的发展以及人类对太空的深入探索，空间机器人被期望在太空服务中扮演更重要的角色并能执行更复杂的任务(如失效航天器的维修、在轨燃料加注、在轨装配和后勤支援等)，以实现延长在轨航天器服务寿命、提升在轨服务性能的目的，因此对其的研究引起了国内外学者的诸多关注[1-7]。为了实现上述在轨服务任务，空间机器人对目标航天器的捕获操作能力是其中不可或缺的一项关键技术，对空间机器人捕获航天器操作的研究已逐渐引起研究人员的重视[8-10]。

空间机器人系统进行捕获操作时，一般包含4个阶段：(1)观测阶段，对目标航天器进行参数估计、辨识。(2)接近阶段，使空间机器人到达可抓捕区域。(3)接触、碰撞阶段，空间机器人系统对航天器进行捕获操作。(4)镇定运动阶段，对空间机器人与航天器形成的失稳混合体系统进行镇定控制。由于执行第(3)阶段时，空间机器人与航天器的接触、碰撞过程不可避免地会产生较大的冲击力矩，若关节所受冲击力矩过大，将对关节造成冲击破坏，进而导致空间任务失败。现阶段仅采用极小的相互接近速度来减小冲击力矩，虽然该方法对合作目标是可行的，但对具备逃逸装置的非合作目标基本上是无法实现的。因此，在(3)～(4)阶段采取一定措施以避免这种冲击、碰撞对关节执行器造成破坏，此项研究有着重要的探索价值和意义。

国内外学者经过多年研究，对空间机器人捕获航天器操作的运动学和路径规划问题，已经取得了大量成果。张旭等[11]针对在轨捕获的路径规划问题，提出了一种基于控制变量参数法的策略。Stolfi等[12]提出了一种用于控制双臂空间机械手捕获非合作目标的阻抗控制方案。Meng等[13]针对含柔性构件空间机器人自主捕获目标前的弹性振动抑制问题，基于动态耦合模型设计了一个闭环控制系统。梁捷等[14]讨论了碰撞后稳定运动控制方案。Virgili-L等[15]通过地面实验模拟验证了装备机械手的航天器自主捕获驻留空间物体的方法。但是，国内外关于空间机器人在捕获操作过程中如何避免其关节免受冲击破坏的研究却鲜见报道。

考虑到研究现状，本文针对空间机器人在轨捕获航天器过程避免关节受冲击破坏的控制问题，将RSEA(Rotary Series Elastic Actuator)装置引入到空间机器系统，同时设计了结合适时开启、关闭关节电机的控制策略以实现避撞柔顺控制。这是因为RSEA装置在机器人与外界环境发生碰撞时，在缓冲、保护机器人关节执行器避免外部冲击破坏方面发挥了很好的作用[16-17]。然而由于RSEA装置存在缓冲弹簧，因此也为系统带来了关节柔性。因此，本文基于奇异摄动理论，将空间机器人与被捕获航天器形成的混合体系统分解为表征柔性部分的快变子系统及表征刚性部分的慢变子系统。针对快变子系统，设计了速度差值反馈控制器，以实现系统弹性振动的主动抑制。针对慢变子系统，提出了基于无源性理论的神经网络鲁棒H∞控制器。该控制方案秉承了无源性理论本身具有的良好动态特性及较强的鲁棒性[18]，可快速实现捕获操作后混合体系统受扰运动的镇定。最后通过对含RSEA空间机器人系统捕获航天器进行数值仿真，仿真结果验证了该避撞柔顺控制策略的正确性。

2 柔顺机构结构及避撞策略

含柔顺机构空间机器人系统的机械臂关节由电机通过RSEA传动装置驱动，本文所设计RSEA传动装置的驱动结构如图1所示。其由输入圆盘(与外部电机相连)、传动弹簧组、支撑中轴和输出扫臂组成。3只扫臂为星形且呈120°均布，每只扫臂通过轴承与固定在输入圆盘上的支撑中轴连接；3组安装在输入圆盘的附加挡块与扫臂之间的弹簧组，呈内接等边三角形布置，每组有2根弹簧，共同驱动其相对应的扫臂。图中R为弹簧端面圆心到支撑中轴中心的距离，r为弹簧的半径。

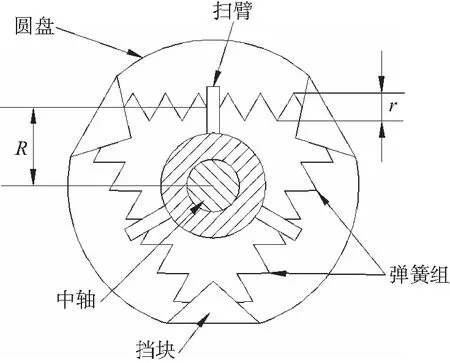
图1 RSEA装置结构图Fig.1 Structure of RSEA

在捕获接触、碰撞阶段，目标航天器与机械臂末端发生碰撞，进而产生了巨大的冲击力矩，该力矩先通过机械臂传递到RSEA装置的扫臂上，扫臂再把力传递给弹簧，通过其内置缓冲弹簧的变形来吸收、缓冲冲击力矩，进而达到减小关节所受冲击力矩的目的。而在镇定运动阶段，受冲击效应的影响，电机开启时也会受到冲击力矩的影响，若所受力矩超过电机所能承受的极限而不关停电机，电机将遭受过载、破坏。基于此，当关节所受冲击力矩大于关节电机能够承受的阈值时，则适时关机，由于关节电机没有力矩的输入，此时RSEA装置的内部弹簧组会提供弹力来减小关节所受的冲击力矩，因此可将关节电机所受冲击力矩限制在安全范围内，进而避免了过大的冲击力矩对关节电机的破坏，实现了对关节电机的保护。同时，因弹簧力作用，空间机器人将进行姿态调整使得关节冲击力矩降低，而在关节冲击力矩低于设置的开机阈值时，则需要适时开机完成失稳混合体系统的镇定。

3 动力学建模及碰撞冲击分析

3.1 空间机器人及目标航天器系统动力学建模

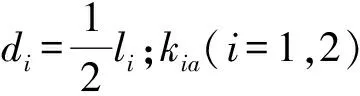
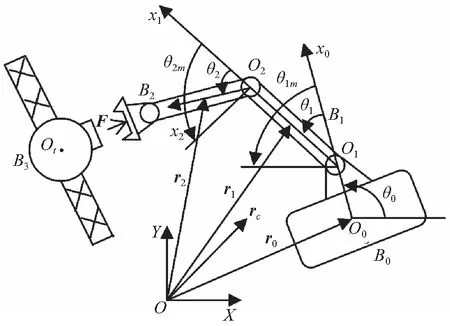
图2 含RSEA的空间机器人系统及目标航天器系统Fig.2 Space robot with RSEA and target spacecraft systems

根据图2的几何位置关系，可得捕获前载体、两杆质心在惯性坐标系下的位置矢量表达式为：

(1)

(2)

其中：xa，ya为载体质心位置坐标；ei(i=0，1，2)为各联体坐标系xi(i=0，1，2)方向的基矢量。

通过对式(1)、式(2)进行求导，并在此基础上，得到含柔顺机构空间机器人系统总动能表达式如式(3)：

(3)

其中：ωi(i=0，1，2)表示载体及两机械臂杆相对于惯性坐标系的角速度，ωjm(j=1，2)表示电机转子相对于惯性坐标系的角速度.。

忽略太空微弱的重力影响，可知空间机器人系统势能只来源于RSEA装置，因而其总势能有：

(4)

其中：ΔxiL=Rsinαi，ΔxiR=-Rsinαi；ΔxiL，ΔxiR分别表示为其左右侧弹簧变形量，αi为输入圆盘与扫臂之间的角度差。

基于上述总动能、势能表达式，结合第二类拉格朗日方程，可得捕获碰撞前载体位置不受控制，姿态受控制的空间机器人动力学模型为：

(5)

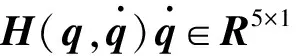
将被捕获航天器视为均质刚体，则可通过牛顿-欧拉法获得被捕获航天器系统的动力学模型：

(6)

其中：Dt∈R3×3为被捕获航天器具有对称、正定性的惯量阵，qt=[xt，yt，θt]T为被捕获航天器的广义坐标列向量，xt，yt为其质心位置坐标，θt为航天器姿态转动角；Jt∈R3×3为其碰撞接触点对应的运动Jacobian矩阵，F′∈R3×1为航天器所受作用力。根据牛顿第三定律，其满足F=-F′。

3.2 捕获目标航天器过程碰撞冲击效应分析

空间机器人系统对目标航天器进行捕获操作时，两者末端所受作用力满足牛顿第三定律，基于此并结合式(5)、式(6)，可得：

(7)

由于空间机器人系统对目标航天器进行捕获操作过程未受外力作用，所以整个系统满足动量守恒，因此，对式(6)两端进行积分并整理得[11]：

(8)

其中t0为捕获接触时刻，捕获完成后，两者形成混合体系统。对于混合体系统，空间机器人末端与目标航天器接触点满足速度约束，即：

(9)

结合式(8)、式(9)，可得捕获后混合体广义速度：

(10)

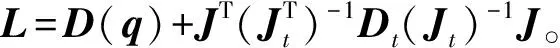
对式(5)第1项进行积分，并整理得：

(11)

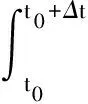
(12)

其中(JT)+1为JT的伪逆，且(JT)+1=J(JTJ)-1。由于捕获碰撞时间Δt极小，则碰撞力可以近似为：

(13)

3.3 捕获完成后混合体系统动力学模型

空间机器人对航天器完成捕获后，两者形成混合体系统，即式(9)恒成立。对式(9)求导，可得：

(14)

结合式(5)、式(7)、式(14)，可得混合体系统动力学模型为：

(15)

考虑空间机器人系统在轨服务寿命等原因，载体位置处于不受控的状态。所以，式(15)为欠驱动形式，不利于控制的设计。为将式(15)化为全驱动形式，将其写成分块子矩阵形式：

(16)

(17)

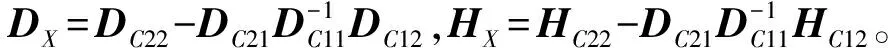
4 控制器设计

4.1 快变子系统控制器设计

考虑RSEA装置的引入使得系统关节具备柔性，其将导致机械臂运动过程产生弹性振动，为了抑制弹性振动，基于奇异摄动理论，将混合体系统分为快变子系统和慢变子系统分别进行控制。因此，系统的总控制律可写为如下形式：

τm=τs+τf，

(18)

其中：τs∈R2×1为慢变子系统控制力矩，τf∈R2×1为快变子系统控制力矩。

定义Γ=Km(θm-θ)为系统“快”变量。假设正比例因子ε及正定对角阵K1，并令其满足：

(19)

将式(19)代入式(17)下面两个方程，得到如下形式描写系统弹性振动的快变子系统方程：

(20)

针对快变子系统，采用速度差值反馈控制器：

(21)

将式(18)、式(21)代入式(20)，可得：

(22)

当ε→0时，关节等效刚度Km→∞，混合体系统等效为刚性模型；则由式(17)、式(18)可得出慢变子系统的动力学方程：

(23)

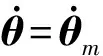
4.2 慢变子系统控制器设计

针对所得到的慢变子系统动力学方程，对HSθ适当选取，可使其满足如下关系：

(24)

因为捕获目标为非合作航天器，所以捕获操作将导致系统的惯性参数无法精确获得，且参数的摄动是难以避免的，因此，存在着建模误差，即有：

(25)

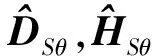
定义慢变子系统相关误差矢量为：

(26)

其中qθd∈R3×1为系统期望位置矢量。

2017年全国煤层气勘探开发投入24.19亿元，共钻探井123口、开发井506口。新增煤层气探明地质储量104.8亿立方米，同比减少81.8%，地面开发的煤层气产量47.04亿立方米，同比增长4.6%。

针对系统标称模型，设计如下形式控制器：

(27)

将式(27)代入式(23)，可得：

(28)

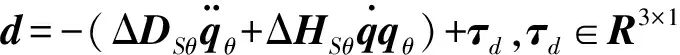
为便于分析，引入如下状态空间变量：

(29)

其中λ为正常数。若不考虑建模误差及外部扰动项，则慢变子系统(28)可改写为如下状态空间方程：

(30)

定义系统输出信号为：

y=z2，

(31)

定义能量函数为：

(32)

对式(32)进行求导，可有：

(33)

根据式(33)，选取如下控制器：

(34)

结合所设计控制器，式(34)可化简为如下：

(35)

将ν视为系统输入，则该系统满足传统的无源性控制理论[18]，因而输入ν到输出y是无源的。

考虑建模误差及外部扰动项是不可忽略的因素，为了实现对慢变子系统的精确控制，必须对总扰动项d进行补偿，则式(35)应写为：

(36)

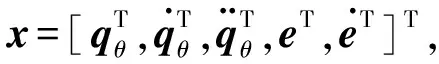
(37)

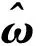
(38)

其中bi，δi分别为高斯基函数相对应的函数中心及宽度。同时，对于任意小的正数σ，存在网络最优权值ω*，使其满足：

(39)

基于以上RBF神经网络补偿项，对控制器进行如下：

(40)

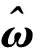
(41)

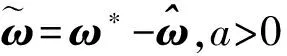
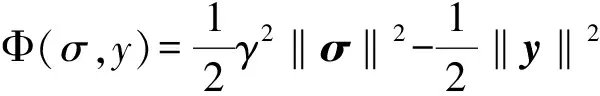
证明：定义如下Lyapunov函数：

(42)

对式(42)进行求导，可得：

(43)

令最优逼近误差σ为外部干扰，同时选取：

(44)

将式(43)代入式(44)，可得：

(45)

由式(45)可知：

(46)

5 仿真算例

5.1 捕获碰撞过程RSEA抗冲击性能模拟

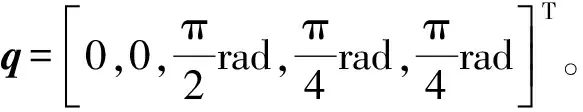
Km=2Ka(3R2+r2)(2cos2φ-1)，

(47)

其中：Ka=diag(k1a，k2a)，R=0.1 m，r=0.01 m，φ为机械臂末端施加τF=[20 N·m，20 N·m，0 N·m]T的载荷时扫臂的转角，仿真时选取φ=diag(3°，2°)。

为了验证RSEA装置在捕获碰撞过程的抗冲击性能，采用未配置与配置RSEA装置空间机器人对3组不同速度航天器进行捕获碰撞仿真模拟，并计算碰撞过程关节所受冲击力矩，结果如表1所示。

表1 航天器不同初速度下RSEA的抗冲击性能模拟

表1中，第1列为航天器速度项，前2项为线速度，单位为m/s，第3项为角速度，单位为rad/s；第2、3列为关节1、2所受冲击力矩，其中，前、后项分别为未配置与配置RSEA装置关节所受冲击力矩，冲击力矩单位为N·m。第4列为冲击力矩最大降低百分比。

由表1可看出，由于RSEA装置内置弹簧的缓冲作用，针对不同初速度航天器的捕获接触过程，都可通过机械臂把力矩传递给RSEA装置的弹簧组使得弹簧拉伸或压缩，进而把冲击能量存储在弹簧组里；较未配置RSEA装置的空间机器人，各关节冲击力矩均得到有效降低，从而实现了对关节电机的保护。

5.2 镇定运动过程避撞柔顺控制策略性能模拟

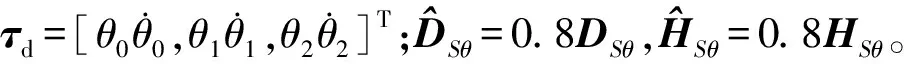
图3给出了镇定运动阶段未结合主动开、关机策略时，关节电机所受冲击力矩。此时，空间机器人虽然因其配置的RSEA装置降低了冲击力矩，但仍然超出安全阈值，因此结合适时开、关机策略进行控制。本文设置电机关机阈值为τO=60 N·m，开机阈值为τI=10 N·m。图4及图5分别为开启本文所提开、关机策略时，关节电机所受冲击力矩及关节电机开关机情况。此时，当关节所受冲击力矩大于设定关机阈值时，电机适时关闭，由于没有外部力矩输入， RSEA装置的内部弹簧组会提供弹力来减小关节所受冲击力矩；同时，因弹簧力作用，空间机器人将进行姿态调整，使得冲击力矩降低，当冲击力矩低于开机阈值时，电机再次开启。对比图3与图4可知，所提策略实现了对关节电机的保护。

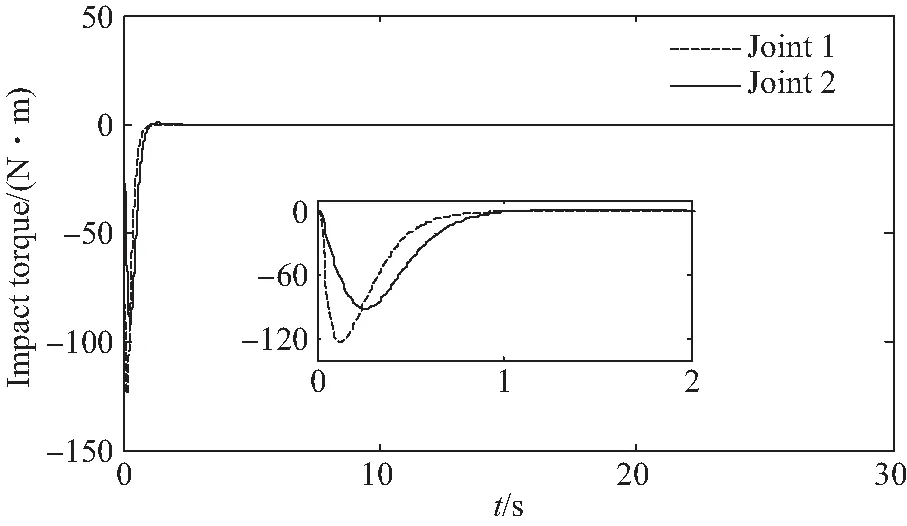
图3 未开启开、关机策略关节所受冲击力矩Fig.3 Joint impact torque without switching strategy

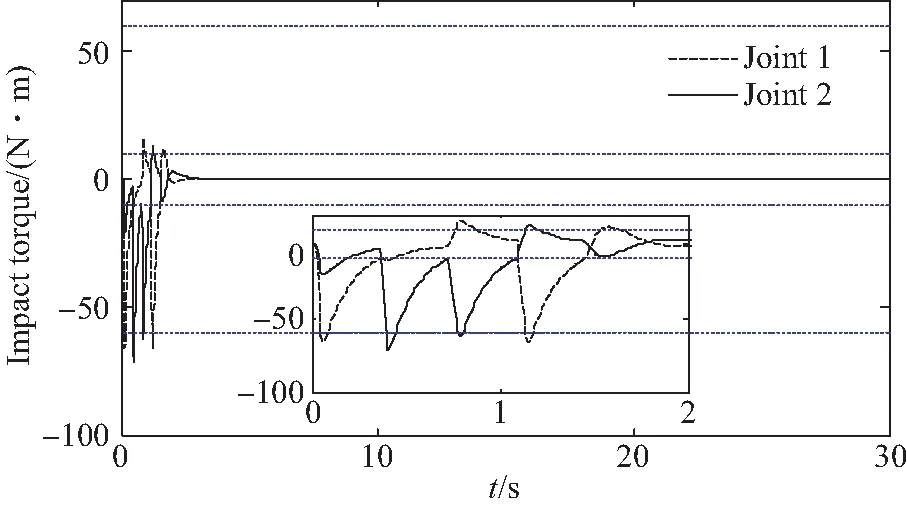
图4 开启开、关机策略关节所受冲击力矩Fig.4 Joint impact torque with switching strategy

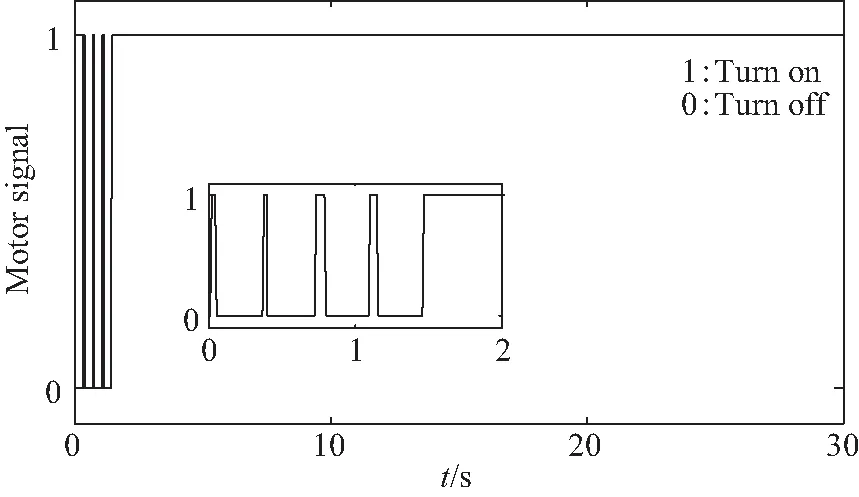
图5 开、关机信号Fig.5 Switch signal of joint motor

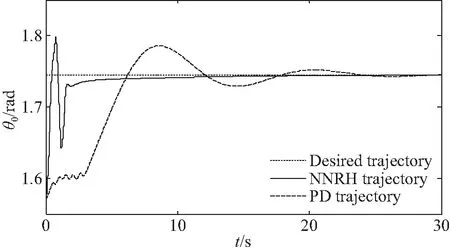
图6 姿态角轨迹跟踪情况Fig.6 Trajectory tracking of attitude angle

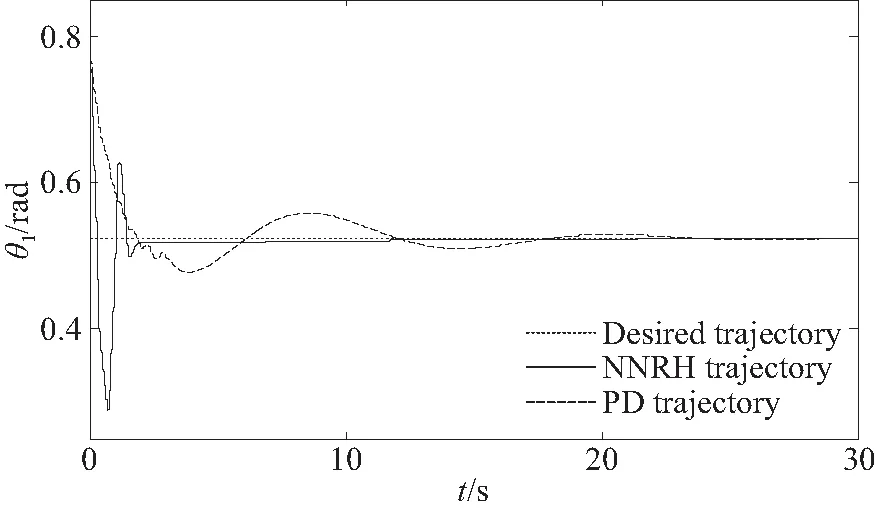
图7 关节1轨迹跟踪情况Fig.7 Trajectory tracking of joint 1

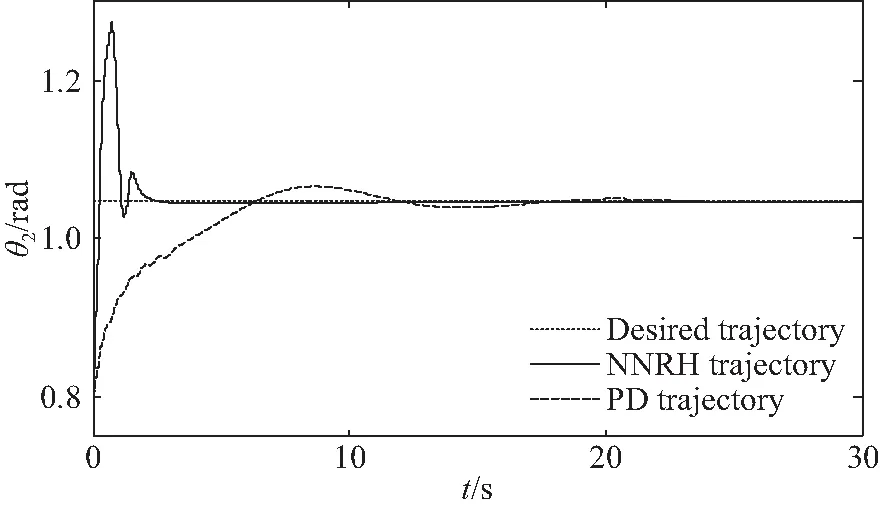
图8 关节2轨迹跟踪情况Fig.8 Trajectory tracking of joint 2

图6～图8为开启开、关机策略时的镇定轨迹，分别采用文中所提基于无源性的神经网络鲁棒H∞(Neural Network Robust H-infinity， NNRH)算法与文献[10]所提PD算法进行镇定控制。对比轨迹跟踪情况可知，由于PD控制鲁棒性较差，因此对失稳联合体系统镇定所需时间较长，而所提基于无源性的神经网络鲁棒H∞算法具备较强的鲁棒性，因此其较PD控制，可更快实现对受扰动混合体系统的镇定控制，并达到轨迹的精确跟踪。

图9～图11为关闭其快变子系统速度差值反馈控制器时，所得的跟踪轨迹。由于系统存在关节柔性，因此混合体系统将产生柔性振动，并最终导致系统产生不稳定运动。比较图6～图8与图9～图11可知，开启所提速度差值反馈控制器，可实现对系统关节弹性振动的主动抑制，进而达到轨迹的稳定及精确跟踪。

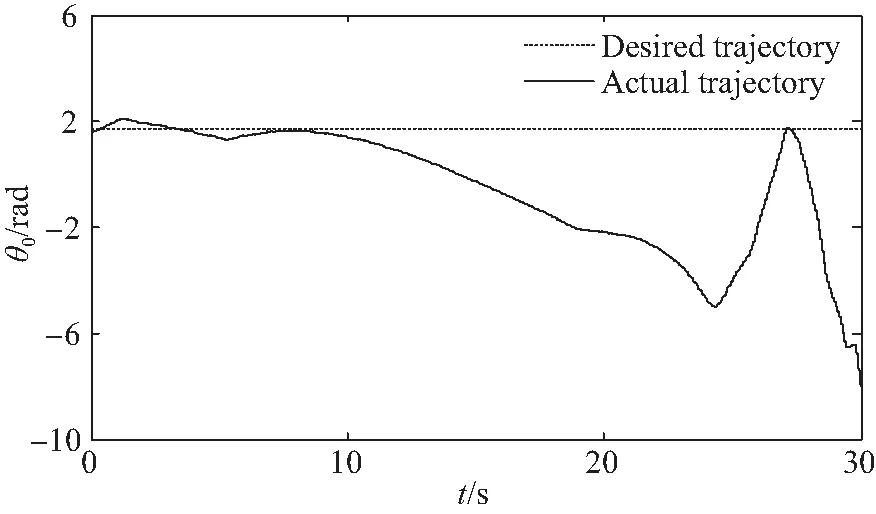
图9 关闭快变控制器姿态角轨迹跟踪情况Fig.9 Trajectory tracking of attitude angle without fast controller

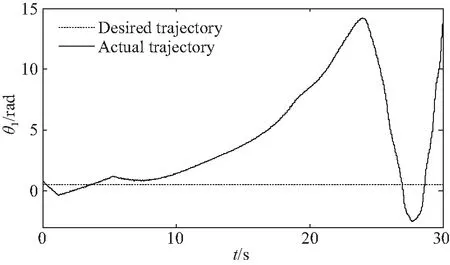
图10 关闭快变控制器关节1轨迹跟踪情况Fig.10 Trajectory tracking of joint 1 without fast controller

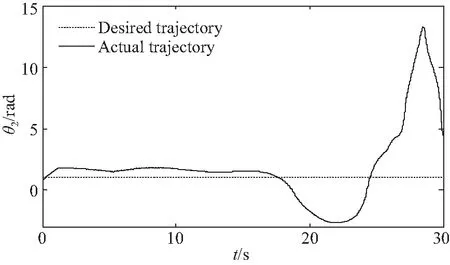
图11 关闭快变控制器关节2轨迹跟踪情况Fig.11 Trajectory tracking of joint 2 without fast controller

5 结 论

为了避免空间机器人在捕获操作过程中冲击力矩对关节电机造成破坏，本文设计了一种含RSEA装置的空间机器人，并提出了主动开、关关节电机的避撞柔顺控制策略。通过仿真试验可知，含RSEA传动装置的空间机器人在接触、碰撞阶段可减小关节所受碰撞冲击力矩47.8%～61.9%，具有良好的抗冲击性能，有效地缓冲了接触、碰撞阶段所受冲击力矩。而镇定运动阶段，结合合理设置的主动开、关机策略，可将关节电机所受冲击力矩限制在安全范围内，避免了过大的冲击力矩对关节电机的破坏，进而实现了对关节电机的保护。此外，上述系统经过适当扩充，可推广应用于三维运动的空间机器人系统。