浮选气泡NSCT域多尺度等效形态特征提取及识别

黄凌霄，廖一鹏

(1.阳光学院 人工智能学院，福建 福州 350015；2.福州大学 物理与信息工程学院，福建 福州 350108)

1 引 言

地球上的铁、铜、锌等矿物都需要经过精选处理后再利用，浮选法是最重要的处理方式，其中的核心部分是气泡层，因此它在表层的特征与工业生产直接挂钩[1-3]。传统方式是通过眼睛观察气泡表面状态来估计矿物品质，但这种方式效率不高、主观性强、精确度较低，容易造成矿物的流失。随着图像处理技术的迅猛发展，通过计算机图像识别技术，对气泡表层图像进行分析以预测选矿质量，获得了广泛地应用[4]。

浮选气泡具有动态、连续、大量紧密靠近、无背景、尺寸不一且拥有难以察觉的边缘等特点，导致气泡提取困难。浮选气泡的特征提取是状态识别中最为关键的技术之一，图像提取的效果很大程度上决定了分类识别率的高低。目前，国内外主要采用的方法是区域分割和边缘检测：区域分割方法采用改进的标记分水岭分割算法提取气泡[5-6]，不适用于不均匀气泡。王卫星等[7]提出采用谷点边界检测气泡算法，虽然检测效率高，但参数需要人工干预。廖一鹏等[8]采用和声搜索谷底检测，提高了检测率，但对于不均匀气泡，采用全局最优参数鲁棒性不强，且大气泡存在伪边界。通过图像分割的方法获得的特征，不具有多尺度，不够全面完整。因此，寻找一种更精准全面的特征提取方法已成为模式识别的热点方向之一。

近年来，研究者提出了一种较新的图像边缘检测方法——多尺度几何分析(Multiresolution Geometric Analysis， MGA)[9-10]，以达到更深层次、更全面地获取图像信息的目的。常用的方法有傅里叶变换、Gabor滤波、小波变换[11]、 Contourlet变换[12]及非下采样Contourlet变换(Nonsubsampled Contourlet Transform，NSCT)[13-15]等。刘金平等[16]通过对浮选气泡图像进行Gabor小波变换，从而提取纹理特征，并对浮选工况进行模糊聚类分析与状态识别，虽然小波变换能同时在时域和频域对图像数据进行多尺度分析，但缺乏形态学意义；彭涛等[17-18]将图像二值化与小波多尺度分析相结合，通过小波多尺度二值化以获取浮选气泡图像的等效尺寸特征，然后对浮选气泡图像进行分类，但提取的特征数不够，且图像的方向性有限，分解的图像只能得到水平、垂直和对角线方向的子图像，无法精确获得图像的边缘信息；刘欢等[19]通过Contourlet变换提取出分形维的图像特征，具有多方向性，对图像的方向性纹理信息及轮廓具有高效的表示能力，但没有平移不变性的，可能会导致“振铃”现象的产生。非下采样Contourlet变换具有Contourlet变换的多尺度多方向特性和平移不变性，进而可以有针对地提取浮选气泡图像的多尺度特征及细节信息。Li等[20]提出了一种在传统神经网络中引入量子旋转门和受控非门的量子门节点神经网络算法，构造新的网络模型，再结合梯度下降算法进行参数优化，实验表明，该算法很好地结合了神经网络的分类识别特性和量子计算的并行特性，网络的收敛速度更快，分类效果更好。

鉴于以上分析，本文提出一种NSCT域多尺度图像特征提取与人工智能相结合的方法，实现了浮选气泡图像多尺度等效形态特征提取及状态识别。首先，采用NSCT多尺度变换算法对浮选气泡图像进行分解，得到气泡的多尺度图像；采用模糊集二值化方法对低频图像进行亮点提取，计算出亮点个数、面积、标准差和椭圆率等形态特征；以方向模极大值为输入，采用差分盒维法计算得到高频多尺度图像的分形维数；最后，将多尺度等效形态特征作为气泡图像状态识别的输入，利用量子门节点神经网络对三类浮选气泡图像进行分类，并通过实验对提出的方法进行了验证。实验结果表明，该方法能够有效地区分三类浮选气泡图像，平均识别准确率较高。

2 NSCT变换

M.N.Do等提出了NSCT变换[21]，NSCT是一种新型的平移不变、多尺度、多方向性的变换，它是基于非下采样金字塔(Nonsubsampled Pyramid，NSP)和非下采样方向滤波器(Nonsubsampled Directional Filter Bank，NSDFB)的一种变换。气泡进行NSCT分解流程如图1所示，首先通过NSP对输入图像进行k次多尺度金字塔形分解，分解为1个低频子带图像和k层高频子带图像，再由NSDFB将高频子带图像分解为2l个方向子带。由图可见，气泡图像的信息主要集中在低频子带，而高频子带主要体现了纹理和轮廓等信息。

图1 浮选气泡图像的NSCT分解图Fig.1 NSCT decomposition of flotation bubble image

3 NSCT域多尺度等效形态特征提取

3.1 模糊集二值化的低频子带特征提取

模糊技术作为非线性科学的一种基础方法，不仅能够充分依靠其鲁棒性去除图像灰度的不确定性，还能有效地减少背景中的干扰，适合解决工况浮选气泡图像质量差、噪声多、边缘不确定等问题。同时，基于模糊集技术的二值化方法可自动获取最佳阈值，具有自适应性，满足工况浮选图像动态变化的要求。

3.1.1 模糊集和隶属度函数[22]

首先，假定X为一张大小为M×N、具有L个色阶的灰度图像，xmn代表图像X中点(m，n)的像素灰度值，定义从图像X映射到[0，1]区间的模糊子集如下：

X={xmn，μX(xmn)}，

(1)

其中：μX(xmn)为点(m，n)的隶属度值，0≤μX(xmn)≤1，m=0，1，…，M-1，n=0，1，…，N-1。

定义h(g)表示灰度级为g的像素的个数，对于给定的阈值t，背景和前景的色阶平均值分别为μ0和μ1，则对于图像二值化来说，则隶属度函数可定义为：

(2)

其中：C为常数，可取C=gmax-gmin，gmax为最大色阶，gmin为最小色阶，C使得0.5≤μX(xmn)≤1。

3.1.2 模糊度的度量和最优阈值选取原则

模糊度表示了一个模糊集的模糊程度，本文使用香农熵函数来度量模糊度。一幅有L个色阶的灰度图像X的熵可以表达为：

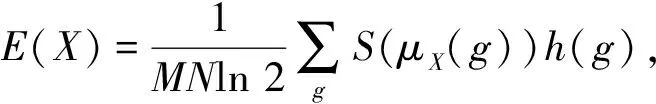
(3)

对于图像X，最佳的阈值选取原则是：按某种规则改变阈值t，计算模糊度，找到整个过程中最小模糊度对应的阈值t，即为最佳的分割阈值。该过程由算法自动完成，无需人为调整。

浮选气泡图像经过NSCT分解后得到多尺度子带，采用模糊集二值化方法得到最佳的分割阈值，对低频图像进行处理，得到较为准确的气泡二值化亮点图像。然后对低频子带的亮点图像进行等效形态尺寸特征提取和计算。假设求得二值图像的亮点个数为N，则亮点的面积平均值、标准差分别为：

(4)

(5)

其中：i∈[1，2，…，N]，各个亮点的面积分别为S1，S2，…，SN。

区域的椭圆率是区域形状的重要描述。假设区域对应的等效椭圆焦距为c，长半轴为a，则区域的椭圆率e=c/a。

对于灰度均匀的区域，椭圆率越大，则区域形状越接近椭圆形，以此可以用来区分椭圆形亮点居多的黏性气泡和另外两类气泡。

3.2 模极大值分形维数的高频子带特征提取

高频子带主要表示浮选气泡的纹理、边缘等细节信息，通过对比三种常用的纹理特征表示方法，灰度直方图计算简单，不够精确；灰度共生矩阵的计算较复杂，且维度略高，降维处理会丢失许多图像细节特征；分形维数只有一维，结合浮选气泡图像自相似的结构特点，本文使用分形维数表示高频子带图像的纹理参数。

(6)

其中L为某尺度的方向数。进行方向模极大值判断后，获取高频子带的边缘分量，将其作为输入来计算分形维数，该方法相较于传统的方法，提取的信息更丰富、更准确。

1975年，Benoit B.Mandelbrot认为自相似性的表面包含分形特征，提出将分形维数运用于图像纹理分析。若M为n维欧氏空间中的有界集合，且可以表示为其自身的Nr个互不覆盖的子集的并时，则M是自相似的且具有分形特征。M的分形维数D定义如下[23]：

(7)

其中：r是尺度大小，Nr表示集合M互不包含的子集个数。

本文采用差分盒维法计算分形维数。差分盒维法(Differential Box Counting，DBC)是由GANGEPAIN等[24]提出的一种计算分形维数的高效快速的方法。

分形维数算法要求图像尺寸为2r，根据r值求得正方形区域的坐标，并提取该区域中的最大值和最小值；在不同的度量尺度r下，分别求得该尺度下的Nr，得到一组数据；对该组数据进行最小二乘法线性回归，其斜率即为分形维数D。

4 量子门神经网络状态识别

4.1 量子位与量子门

量子是量子信息的计量单位，它可以同时处在两个量子态的叠加态中，即：

|φ〉=α|0〉+β|1〉，|α|2+|β|2=1，

(8)

其中α和β称为概率幅。

对量子位状态进行变换，实现某些逻辑门的功能，称在一定时间间隔内实现逻辑变换的装置为量子门。目前量子门有很多种，选择常用的量子旋转门R(θ)和量子受控非门C(k)，定义如下：

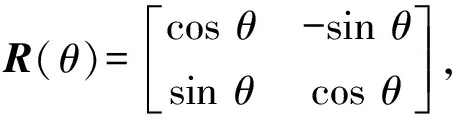
(9)

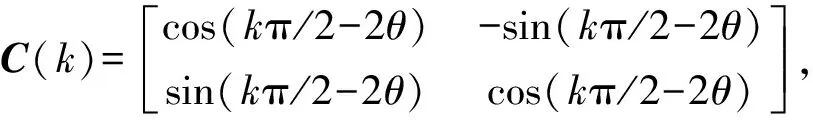
(10)

其中：θ表示旋转角，常数系数k∈[0，1]。

4.2 量子门神经网络模型

量子门节点神经网络[20]，是一种具有代表性的新型神经网络[25-26]。原理如图2所示，其中，|x1〉，|x2〉，…，|xn〉为输入，|h1〉，|h2〉，…，|hp〉为隐层输出，|y1〉，|y2〉，…，|yn〉为网络输出。

图2 量子门节点神经网络Fig.2 Quantum gated neural networks

令输入样本的量子态为：

(11)

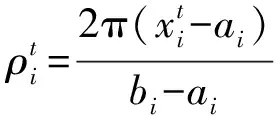
根据量子旋转门与多位受控非门可得：

(12)

(13)

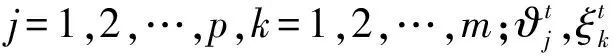
(14)

(15)

其中θ和φ分别表示隐层幅角偏置矩阵和网络输出层幅角偏置矩阵。

图3 梯度下降学习算法流程图Fig.3 Gradient descent learning algorithm flow chart

假定以状态|1〉作为实际输出，则网络各层的实际输出为：

(16)

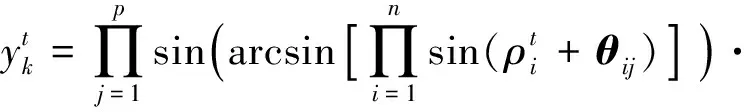
(17)

最后，结合梯度下降学习算法可以精确定位量子神经网络隐含层幅角偏置矩阵θ和网络输出层幅角偏置矩阵φ的全局最优解，具体算法流程图如图3所示。

5 多尺度特征提取和识别步骤

浮选气泡NSCT域多尺度等效形态特征提取及状态识别的实现如图4所示。

Step1：图像NSCT变换：对浮选气泡图像进行灰度化；再采用NSCT方法对图像进行多尺度多方向分解，得到1个低频子带和3个尺度8×3个方向的高频子带图像。

Step2：图像二值化：采用模糊集方法对低频子带图像进行二值化，自动获得最优阈值，得到较精确的低频亮点图像。

Step3：多尺度特征提取：提取二值化后的低频亮点图像特征，包括亮点个数、平均面积、标准差及椭圆率；同时结合方向模极大值和差分盒维法，计算高频子带的分形维数(统计3个尺度8个方向的平均值)。

Step4：量子门节点神经网络分类：将150张浮选气泡图像的尺寸大小及形态等多尺度特征值记录下来，采用基于梯度下降算法的量子门节点神经网络进行训练及测试，统计分析得到分类结果的正确率。

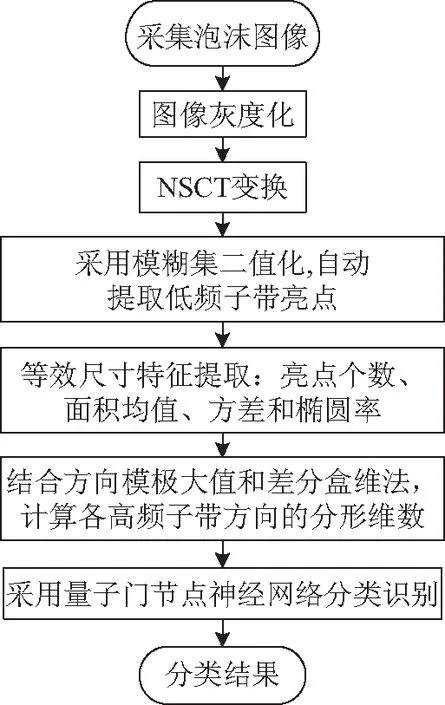
图4 算法流程图Fig.4 Flowchart of proposed algorithm

6 实验与分析

实验以福建金东矿业股份有限公司的铅矿浮选槽为对象。硬件平台为AMD Ryzen 5 2500U显卡为Radeon Vega Mobile Gfx 2.0 GHz，内存为8.00 GB，软件环境为Windows 10 Matlab R2014b。通过大量的实验以验证算法的性能，并对实验结果进行详细地分析和对比。

图5(a)为浮选气泡图像经NSCT分解得到低频图像如图5(b)，高频尺度1图像(图5(c))，高频尺度2图像两个方向(图5(d)和图5(e))，高频尺度3图像4个方向(图5(f)～图5(i))。由图可见，气泡图像的信息主要集中在低频子带，而高频子带主要体现气泡的纹理、边缘和轮廓等细节信息。

(a)原图(a)Original image(b)低频图像(b)Low frequency image(c)尺度1图像(c)1nd scale image

(d)尺度2方向1图像(d)1st direction of 2nd scale(e)尺度2方向2图像(e)2st direction of 2nd scale(f)尺度3方向1图像(f)1st direction of 3nd scale

(g)尺度3方向2图像(g)2st direction of 3nd scale(h)尺度3方向3图像(h)3st direction of 3nd scale(i)尺度3方向4图像(i)4st direction of 3nd scale图5 浮选气泡图像NSCT分解Fig.5 NSCT decomposition of flotation bubble image

正常、黏性和水化三类气泡图像经NSCT分解后，得到正常气泡原图、低频和高频尺度1方向1图像如图5(a)～图5(c)，黏性气泡原图、低频和高频尺度1方向1图像如图6(a)～图6(c)， 水化气泡原图、低频和高频尺度1图像如图6(d)～图6(f)。由图可以看出，三类气泡的尺寸大小和形态特征各不相同，通过NSCT变换后可以体现得更加明显、直观。

(a)黏性气泡图像(a)Viscous bubble image(b)黏性低频气泡图像(b)Low frequency of viscous bubble(c)黏性尺度1气泡图像(c)1nd scale image of viscous bubble

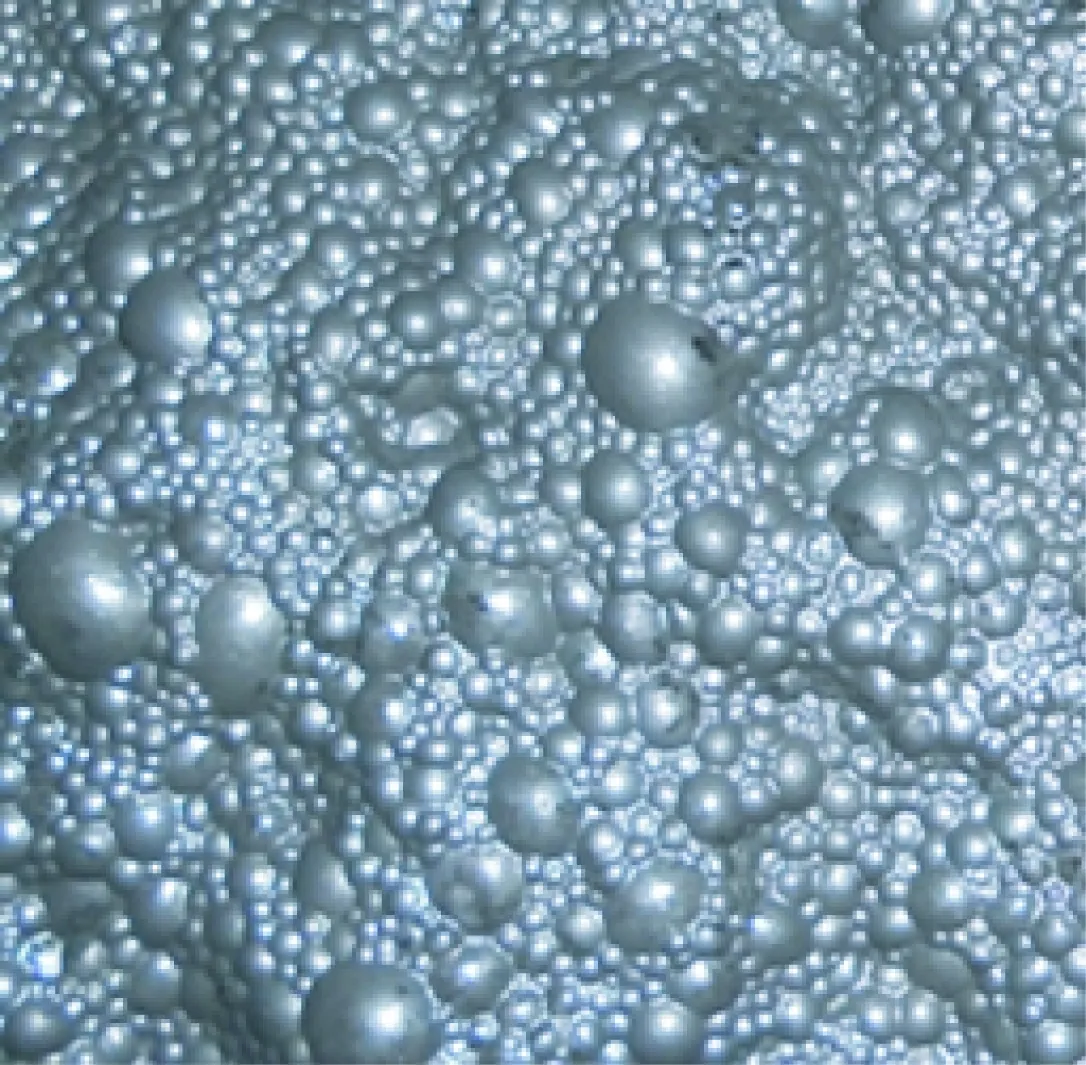
(d)水化气泡图像(d)Hydration bubble image(e)水化低频气泡图像(e)Low frequency of hydration bubble(f)水化尺度1气泡图像(f)1nd scale image of hydration bubble图6 黏性气泡和水化气泡图像多尺度分解Fig.6 Multiscale decomposition of viscous and hydration bubble images

NSCT变换后，采用模糊集方法对低频子带图像(图7(a))进行二值化处理，该方法可以针对不同的图像自动调整阈值，得到较为精确的低频二值化亮点图像。将本文方法与全局阈值、Ostu阈值、迭代式阈值、分水岭分割进行比较，图7(b)是全局阈值实验结果，该方法选取直方图中波谷点的灰度值作为阈值，算法简单，但分割效果不佳，不能如实反映亮点的个数和尺寸大小。图7(c)和图7(d)是Ostu阈值分割和迭代式阈值分割的实验结果，这2种方法都是以最佳阈值实现分割的，虽然亮点基本都提取出来，但都出现了不同程度的亮点粘连，其中Ostu阈值分割是在灰度直方图的基础上采用最小二乘法实现的，而迭代式阈值分割方法是通过迭代的方法求出分割的最佳阈值，具有一定的适应性，所以其实验结果比Ostu阈值分割方法好些。图7(e)是分水岭分割的实验结果，该方法只能大体分割出图像的区域，准确度较差。从本文方法的实验结果(图7(f))可以看出，该方法能准确分割出白色亮点，亮点数量和尺寸与气泡大小一致。

图7(g)～图7(l)分别是正常气泡、黏性气泡和水化气泡的原图及提取的亮点图，可以看出，本文的方法能准确分割出气泡亮点。正常气泡图像亮点尺寸较大，形态大小分布较均匀；黏性气泡图像气泡黏度很高，气泡挤压，甚至呈现长椭圆亮点；水化气泡图像以小尺寸的气泡为主，流动性较强，气泡分布密集。由图可见，亮点图像包含了气泡图像的大部分信息，为准确地进行形态特征提取打下基础。

(e)分水岭(e)Watershed(f)本文方法(f)Proposed method(g)正常气泡(g)Normal bubble(h)正常气泡二值化(h)Normal bubble binarization

(i)黏性气泡(i)Viscous bubble(j)黏性气泡二值化(j)Viscous bubble binarization(k)水化气泡(k)Hydration bubble(l)水化气泡二值化(l)Hydration bubble binarization图7 二值化方法比较及三类气泡实验结果Fig.7 Binary method comparison and experimental results of three types bubbles

通过实验得到三类图像多尺度等效形态特征的直观分布情况对比见图8，统计情况如表1所示。图8(a)和图8(b)为低频亮点图像的4类等效尺寸形态特征，主要提取包括亮点个数、亮点平均面积、标准差及椭圆率等区域尺寸特征。从图中可以看出，三类气泡的4类特征都存在着较明显的差异，其中水化气泡的亮点个数与其他两种类型的气泡差异最大，区分性也最好；亮点平均面积和标准差的差异次之，但也有较好的区分性；黏性气泡由于气泡挤压呈椭圆状，椭圆率较大，通过该特征可以较好地与其他两种气泡区分开。

对原图像进行3层多尺度分解，每个尺度的高频子带图像再分解为8个方向子带，采用模极大值和差分盒维法计算高频子带各方向的平均分形维数如图8(c)所示(鉴于数据量的考虑，本文以3个方向为例)。可以看出，水化气泡的模极大值分形维数较大，正常气泡和黏性气泡较小，相对于低频亮点特征，高频特征的差异性有所降低，但综合低频和高频多尺度特征，还是能有效地区分三类图像，有一定的区分度，可以更深层次、更全面地分析气泡图像，提高分类的准确率。

在相同的入矿条件下，从三种不同工况的浮选气泡图像中各挑出50张图像，共150张。为不失一般性，采用随机法产生训练集与测试集，其中，训练集为：在三类图像中分别随机选取40个样本，共120个样本，测试集为：剩余的30个样本。所有样本进行多尺度特征提取后，通过量子门节点神经网络算法进行训练和测试，所得结果与专家判断对比，得到分类性能。

(a)低频特征1(a)LF character 1(b)低频特征2(b)LF character 2(c)模极大值分形维(c)Modular maximum Fractal dimension图8 三类气泡低频和高频形态特征对比Fig.8 Comparison of morphological characters of three types of bubbles at low and high frequencies

表1 三类气泡形态特征统计数据(平均值)

其中一个样本图像(图9(a))，按照图4算法得到灰度化图像(图9(b))，再通过NSCT变换进行多尺度多方向分解，得到1个低频图像(图9(c))，高频尺度1方向1图像(图9(d))，高频尺度2方向2图像(图9(e))，高频尺度3方向3图像(图9(f))(每个尺度选取1个方向图像)；再采用模糊集方法得到低频子带的亮点图像(图9(g))，并提取亮点图像特征，分别为：亮点411个、平均面积32.8、标准差45.15和椭圆率0.63；结合方向模极大值和差分盒维法，计算出高频子带8个方向的分形维数分别为2.88、2.83、2.83、2.84、2.84、2.85、2.86和2.89；最后，经过量子门节点神经网络测试后被识别为水化气泡，结果与专家判断一致，验证了本算法的有效性。

(a)样本图像(a)Sample image(b)灰度化图像(b)Grayscale image(c)低频图像(c)Low frequency image(d)尺度1方向1图像(d)1st direction of 1nd scale

(e)尺度2方向2图像(e)2st direction of 2nd scale(f)尺度3方向3图像(f)3st direction of 3nd scale(g)亮点图像(g)Highlight image图9 样本图像NSCT分解及亮点提取Fig.9 NSCT decomposition and bright spot extraction of sample image

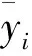
(18)

图10、图11为5类多尺度形态特征与分类正确率相关性结果。

相关系数的统计结果如表2所示。可以看出，低频图像特征：亮点个数、平均面积、椭圆率与气泡分类的相关性较好，相关系数绝对值达0.7以上，标准差相关性一般；高频图像特征：模极大值分形维的相关性较低频特征有所下降，相关系数绝对值约为0.5；其中平均面积、标准差与分类正确率呈正相关，其余特征呈负相关。

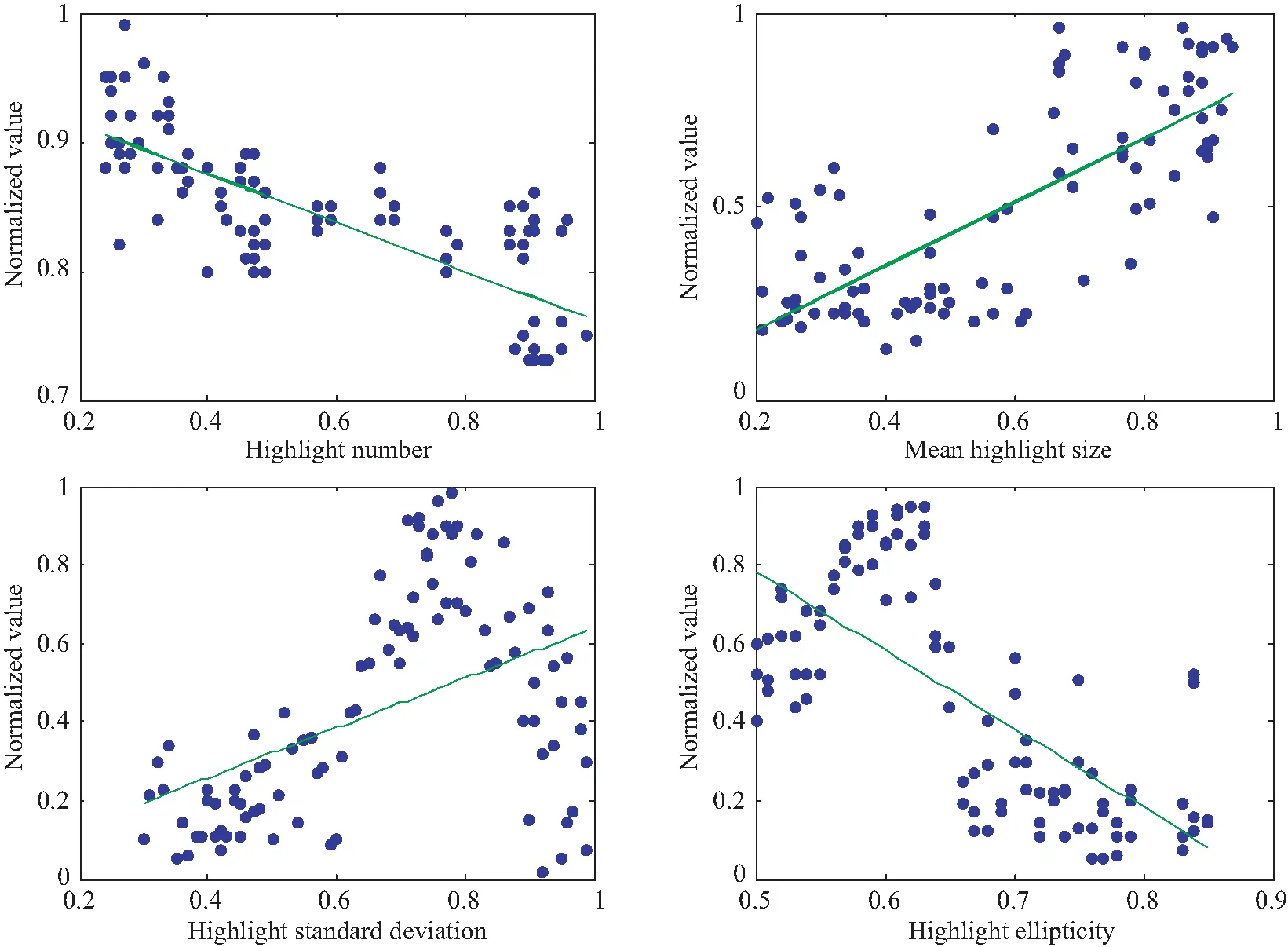
图10 低频形态特征与分类正确率的相关性Fig.10 Correlation between LF morphological characters and classification accuracy

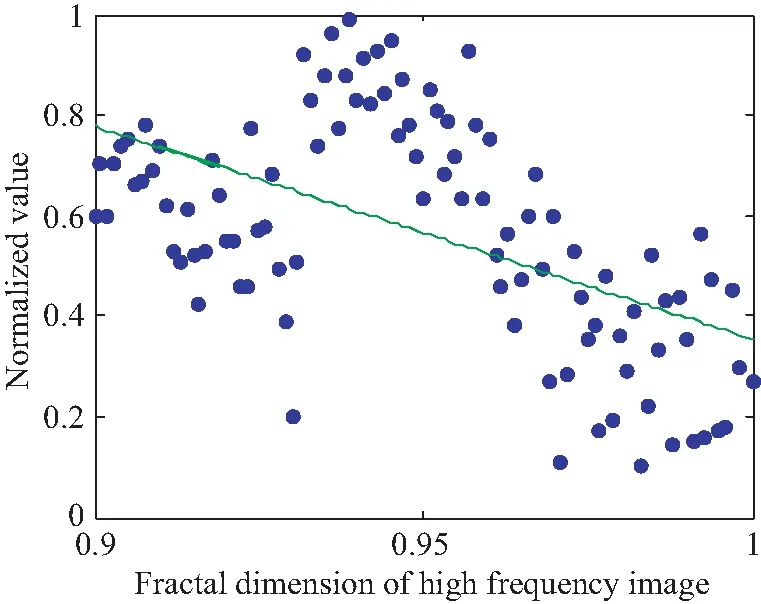
图11 分形维数与分类正确率的相关性Fig.11 Correlation between Fractal dimension and classification accuracy

表2 多尺度特征与分类正确率相关系数统计

为比较不同算法对三类浮选气泡的分类性能，分别运用传统算法、文献[16]算法、文献[17-18]算法、文献[19]算法及本文算法进行气泡分类，得到分类识别正确率，以此来衡量各类算法的性能，结果如表3所示。

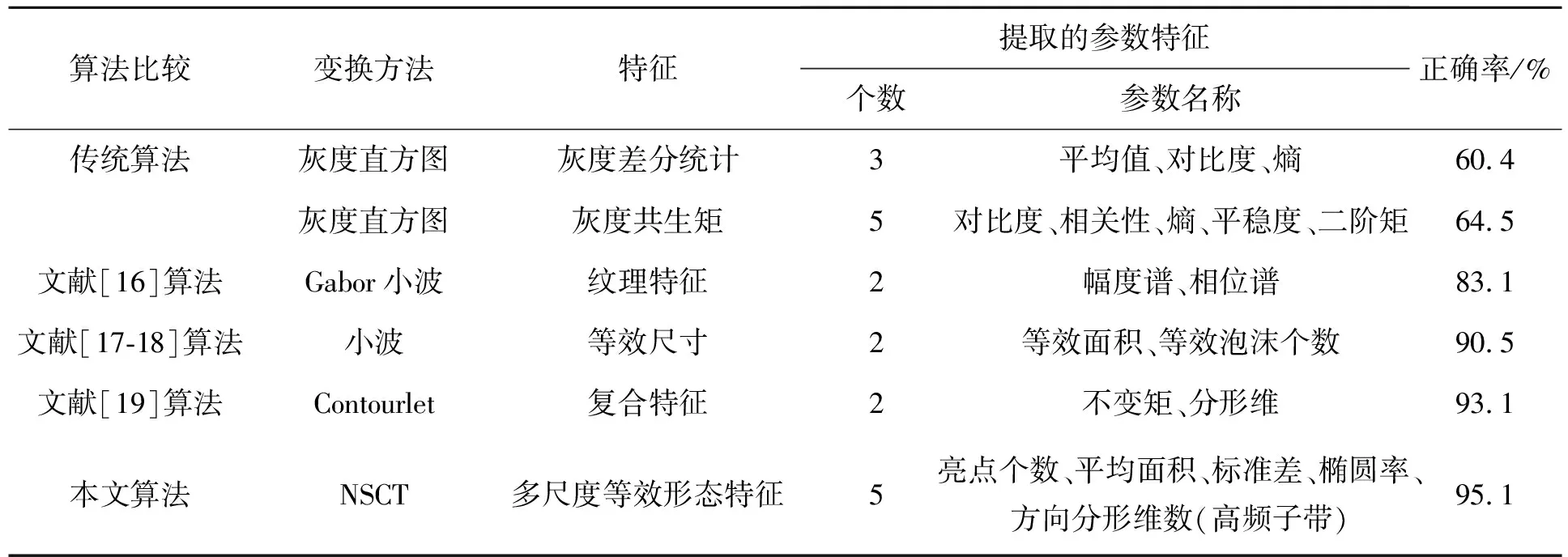
表3 不同算法分类结果评价

由以上统计可以看出，传统算法的特征是直接通过区域分割的方法得到的，不具有多尺度特征，而浮选气泡的相似度很高，直接提取表面特征无法体现不同类气泡的细节和差异信息，不具备可分性，识别正确率较低。文献[16]算法和文献[17-18]算法都是通过小波变换后再提取特征，较传统算法有较大地提升，但由于小波变换很难完整获取图像多方向性的特征，所以识别正确率有局限，无法达到最好的状态。文献[19]算法采用Contourlet变换能够更深入地提取局部特征，有较高的识别率，但提取的特征还不够完整全面，且由于Contourlet变换可能会导致“振铃”现象，稳定性不够，识别率有一定浮动。而在本文算法中，结合多尺度等效形态特征可以有效地对浮选气泡进行状态识别，平均识别正确率达95.1%，较其他算法都更高，稳定度更高，可以满足浮选工况动态变化的需求。

7 结 论

工况浮选气泡图像黏结无背景，气泡边界不明显，相似度较高，对于不同的三类气泡图像，无法达到最好的状态识别和分类。针对这一问题，提出一种基于NSCT域多尺度气泡等效形态特征提取方法。通过对图像进行NSCT域变换，得到多尺度、多方向图像，低频图像通过模糊集二值化方法获得亮点图，提取出基于亮点的4类等效形态尺寸特征，高频多尺度图像提取了表征图像轮廓和细节的模极大值分形维数作为特征参数，以多个等效形态特征作为输入参数，再通过量子门节点神经网络算法进行状态识别和分类，实验结果表明，本文所提取的多尺度特征有很高的区分性，准确性高，对分类产生了显著作用，多类特征组合后的平均分类识别正确率达95.1%，能对三种类型浮选气泡图像进行有效地状态识别。但是，算法中采用的NSCT分解，运算效率不高，因此如何降低算法的复杂度，提高运算效率和工况识别的实时性问题，仍需要进一步研究解决，这也是未来的研究方向。