磁悬浮控制力矩陀螺高速转子的高精度位置控制

汤继强，崔 旭，袁新竹，隗同坤

(1. 北京航空航天大学 仪器科学与光电工程学院，北京 100191；2. 北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室，北京 100191)

1 引 言

控制力矩陀螺(Control Moment Gyroscope，CMG)是一种通过改变角动量方向来调整航天器姿态和抑制干扰的姿控执行机构[1]，主要由高速转子系统和框架伺服系统组成[2]。根据所采用轴承的支承类型，可以被分为机械控制力矩陀螺和磁悬浮控制力矩陀螺(Magnetically Suspended CMG，MSCMG)。由于MSCMG的定转子间存在气隙，因此具有无需润滑、高转速、长寿命、高精度和持续输出大力矩的特点[3-5]。根据框架的个数，CMG可以被分为单框架CMG和双框架CMG[6]。由于框架转动会对转子系统产生耦合力矩和干扰，而相对于双框架而言，单框架对转子系统的耦合力矩与干扰更少，有利于降低控制难度[7]。因此，单框架MSCMG更多地被应用于调整航天器姿态和抑制干扰。

具有大角动量的扁平转子在高速旋转时会产生较强的陀螺效应[8]，使其在平衡位置附近发生较小角度的偏转，转子系统还存在不确定干扰和不平衡振动，这些问题会降低转子悬浮稳定性，增加控制难度。与此同时，框架转动所产生的耦合力矩会使转子跳动量增加(动框架效应)，甚至碰撞保护轴承，严重的会造成转子损伤[9-10]。动框架效应会使转子大角度偏离平衡位置，即磁间隙发生较大变化，造成磁力的刚度系数发生非线性改变，降低磁力控制精度，进而降低转子悬浮稳定性和陀螺的输出力矩精度[11-12]。

高速转子在平衡位置附近发生小角度偏转时磁间隙变化较小，因此磁力的刚度系数所发生的非线性变化对磁力的影响不大，可以对磁力模型进行线性化，因此现有控制方法可以使转子系统稳定悬浮，但不能保证转子悬浮的位置精度。文献[13]采用传统PID(Proportional Integral Derivative)控制方法结合角速率前馈来提高转子系统的稳定性。文献[14]基于PID控制设计了位移和速度交叉反馈器来提高系统的稳定裕度。这两种方法都只考虑了转子的稳定悬浮，并没有对转子大角度偏转时的位置精度进行研究。文献[15]利用含有扩展卡尔曼滤波器和状态反馈调节器的线性二次高斯控制，提高转子位置精度，但是该方法参数多，计算量大，不方便工程应用。文献[16]采用变工作点线性化的方法，根据转子位置采用与之对应的磁力模型，但该方法的控制效果取决于模型精度和不平衡大小等因素。文献[17]提出基于电流刚度估计的自适应控制器，但没有考虑位移刚度的非线性变化。随着航天技术的发展，我国未来发射的航天器在数量和种类上不断增加，传统的控制方法已不能满足新形势下对CMG输出高精度控制力矩的要求。

随着控制理论的发展，智能控制方法和非线性控制方法在解决系统的非线性问题上有很好地表现。文献[18]采用模糊控制器对磁轴承系统进行控制，提高稳定性和鲁棒性，但应用对象为磁悬浮涡轮发动机，不符合CMG输出高精度控制力矩的要求。文献[19]设计了神经网络自适应估计器对磁轴承系统的非线性变化进行估计，提高磁力非线性的稳态精度，但该方法只适用于控制磁轴承轴向平动，而MSCMG转子系统的控制难点在磁轴承径向方向。文献[20]利用BP(Back Propagation)神经网络在线调整PID控制器参数，用于五自由度磁轴承系统悬浮控制。文献[21]利用前馈神经网络逼近磁轴承参数非线性变化。文献[22]利用神经网络来建立磁轴承系统的内模模型。文献[23]设计了自适应模糊神经网络控制器用于磁悬浮传输系统的悬浮控制。文献[24]利用双积分滑模控制系统，调节和稳定高度非线性的磁悬浮转子系统，提高系统的鲁棒性，但是积分运算复杂，计算量大。以上方法侧重于实现磁悬浮转子的稳定悬浮，对提高转子位置精度效果并不理想。由于神经网络具有对非线性函数的逼近能力，被广泛用来逼近非线性函数。而滑模变结构控制是一种特殊的非线性控制器，对参数变化具有鲁棒性，因此应用也比较广泛。将滑模控制结合神经网络用于非线性系统的控制，完成对非线性函数的逼近与补偿，可以取得很好的效果。

本文针对高速转子受陀螺效应和动框架效应影响而偏转时刚度系数非线性变化影响位置精度的问题，建立磁悬浮转子非线性动力学模型并对磁力进行分析，提出神经网络滑模控制算法，用于实现转子的稳定悬浮及提高位置精度。仿真结果表明本文方法在提高位置精度方面比现有方法具有更好的控制性能。

2 转子动力学建模和磁力分析

如图1所示，本文所研究的单框架磁悬浮控制力矩陀螺磁悬浮转子系统主要由磁轴承系统和高速电机系统组成。磁悬浮转子系统包括2个二自由度径向磁轴承和2个一自由度轴向磁轴承，用于实现5个自由度的主动控制；高速电机用于驱动转子高速旋转。轴向位移和径向位移由位移传感器直接测得。基座是连接磁悬浮CMG和航天器的机械结构，CMG的输出力矩通过基座作用到航天器上，实现调整姿态和抑制干扰。

图1 单框架磁悬浮控制力矩陀螺结构图Fig.1 Sectional view of the SGMSCMG

在转子系统上建立空间直角坐标系，如图2所示。磁轴承控制的5个自由度分别是质心在x，y，z3个方向上的平动和绕径向x，y方向上的转动运动。磁轴承力是磁悬浮转子与定子之间的相互作用力，其中，对应Ax，Ay，Bx和By4个通道的磁力分别为fAx，fAy，fBx和fBy，可以合成为X和Y两个方向的径向平动力fx和fy及径向力矩px和py；fz是轴向(z方向)上转子所受磁轴承力的合力；lm表示从磁悬浮转子中心到径向磁轴承中心的距离；α，β分别为转子绕x，y轴正方向的偏转角度；Ω为转子转速。将磁轴承转子质心的平动和转动分别单独考虑，建立转子的平动运动方程和转动运动方程，即可得到磁悬浮转子的动力学模型。

图2 磁悬浮CMG转子系统坐标系示意图Fig.2 Rectangular space coordinate system established on the MSCMG

径向四通道在框架角速率为零(θg=0 (°)/s)且不考虑磁悬浮转子重力的条件下，磁悬浮转子的动力学模型可以描述为：

(1)

其中：m是转子的质量；α，β分别为转子绕x，y轴正方向的偏转角度；Ω为转子转速；转子的赤道转动惯量为Jr，转子的极转动惯量为Jz。

根据磁路安培环路定律进行一系列数学推导可以得到磁力轴承承载力的计算模型：

(2)

其中：μ0为空气磁导率，N是磁轴承线圈绕组匝数，A为定子与转子铁芯间气隙的横截面积，I是线圈电流，h是定子与转子铁芯间气隙的长度，I和h为变量。由于磁力轴承采用差动励磁方式，上下各一个电磁铁，有两个磁力作用于转子，所以转子受到的电磁力为上下磁铁的吸力之差，即：

(3)

其中：F为总电磁力，hm0是径向磁轴承的气隙大小，I0是等效偏置电流，x为转子位移(F与x的方向一致)，i为控制电流。

框架转动会使陀螺效应下的高速转子发生偏转，从而导致定转子间气隙大小发生变化，这会使磁轴承力发生非线性改变。如果仍然采用线性模型，当气隙变化量超过气隙总长度的10%，控制系统的控制难度会增加，系统的稳定性会下降。本文所用的控制力矩陀螺径向磁轴承气隙设计值为0.3 mm，而转子的最大位移能够达到60 μm，这已经远远超过了总长度的10%。因此，考虑磁力的非线性问题是必要的。

表1列出了磁悬浮CMG磁轴承的结构尺寸和相关参数。根据表1的数据和公式(3)，利用MATLAB对转子在Ax通道不同位置处不同控制电流下的磁轴承力作力-位移-电流变化曲线图，如图3所示。可以清楚地看到，当磁悬浮转子被偏离平衡位置时，磁力在不同电流下的非线性变化。当转子偏离平衡位置越远，磁力的非线性程度越高。

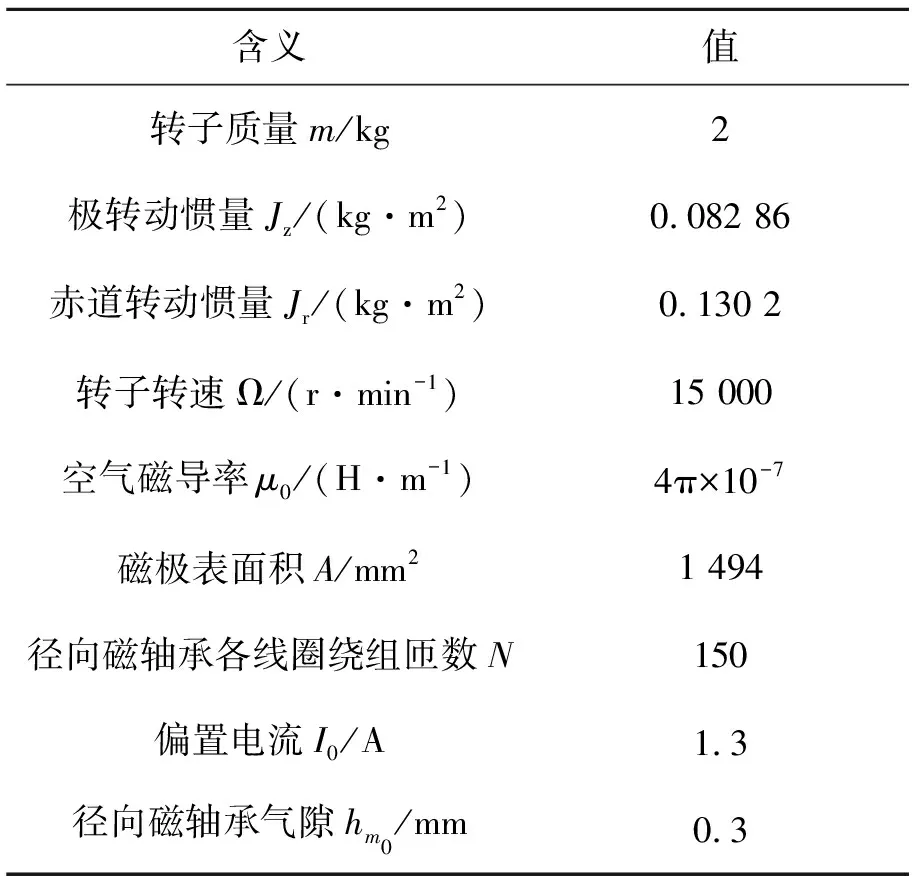
表1 磁悬浮CMG磁轴承结构尺寸及相关参数

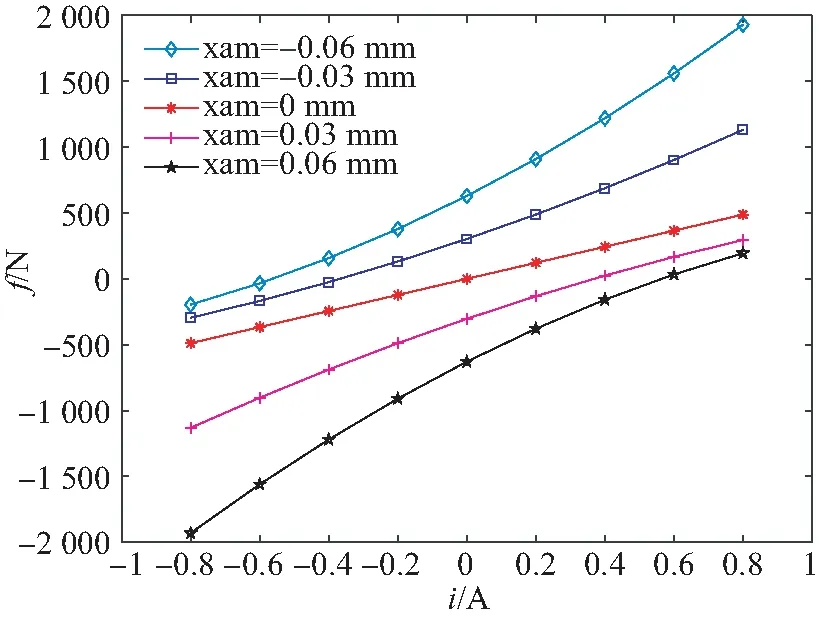
图3 磁轴承力-位移-电流变化曲线图Fig.3 Force-displacement-current curve of MB

利用泰勒展开式分析磁力模型，由于5阶以上影响较小，因此只保留到3阶，可以得到：

(4)

F=kii+khx+kih2ix2+kh3x3+ki2hi2x+on.

(5)

可以看出，磁轴承力模型除了一阶线性项以外，还包含高阶非线性项。为方便说明，将公式(5)的非线性模型取为：

(6)

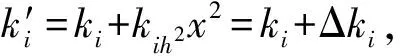
图4 电流刚度随气隙大小变化曲线图Fig.4 Current stiffness-air gap curve

表2 转子小角度偏转和大角度偏转情况下刚度系数变化情况对比表

图5 位移刚度磁间隙-控制电流关系三维曲面图Fig.5 Displacement stiffness-air gap-current surface map

磁悬浮CMG转子在径向不进行主动偏转，偏转角度α，β为转子被动偏转角度，因此径向平动方向的动力学模型为控制核心。将公式(6)代入公式(1)中的径向平动方程，同时考虑到高速转子的奇倍频振动和未建模动态等干扰具有不确定性，因此加入干扰项fd，可以得到：

(7)

其中：fdx，fdy为fd在x，y方向上的分量，ix，iy为x，y方向控制电流。

以x通道为例，磁悬浮转子的动力学方程可以表示为：

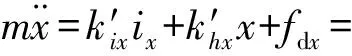
(8)

(9)

当转子大角度偏离平衡位置时刚度系数非线性变化明显，导致转子位置精度下降，使CMG的输出力矩精度降低。因此，需要设计非线性控制方法，提高转子的位置精度从而提高CMG的输出力矩精度。

3 神经网络滑模控制算法设计

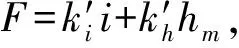
图6 控制系统结构图Fig.6 Structure of control system

3.1 控制器设计

定义转子的位置误差e为：

e=xr-x.

(10)

设计滑模面：

(11)

其中切换参数c>0。

对滑模面函数求导，并将公式(10)代入，可得：

(12)

通过RBF(Radical Basis Function)神经网络对f和g的值进行逼近。RBF神经网络的算法为：

(13)

f=WThf(x)+εf，
g=VThg(x)+εg，

(14)

(15)

(16)

由公式(12)可以导出控制律：

(17)

其中趋近速率η≥D。

3.2 稳定性分析

保持控制系统稳定是实现转子位置高精度控制的基础，而神经网络滑模控制算法的稳定性与控制律中非线性函数的权值调整过程密切相关。利用Lyapunov函数对系统进行稳定性分析，进而可以得到基于自适应算法的网络权值更新规则。

将公式(12)代入公式(11)，可以得到：

(18)

其中：

定义闭环系统的Lyapunov函数为：

(19)

其中：自适应学习率γ1>0，γ2>0。

对L求导并将公式(18)代入，可得：

(20)

设计自适应算法：

(21)

将公式(21)代入公式(20)，可得：

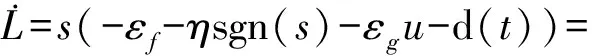
(22)

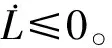
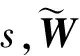
图7是磁轴承径向单通道RBF神经网络滑模控制框图。其中Ka是功放增益，Ks是传感器增益，d为扰动。

图7 单通道RBF神经网络滑模控制框图Fig.7 Control block diagram of single channel

4 仿真和实验结果

为了验证磁悬浮转子系统在刚度系数非线性变化和干扰力的影响下，神经网络滑模控制对转子位置精确控制的有效性，本文基于Matlab/Simulink软件分别搭建了神经网络滑模控制系统和传统PID控制系统，用于比较两种方法的控制效果。首先对转子沿径向X轴方向平动控制进行研究，分别对比两种方法输入信号为正弦和阶跃时的位置精度。其次，在框架转动时高速转子受径向Y通道耦合作用和干扰影响而偏离平衡位置的情况下，对比两种方法对转子期望位置的控制精度，验证本文方法对转子高精度位置控制的有效性。利用实验平台，分别采用传统PID控制和神经网络滑模控制，进行径向单通道的平动控制实验和动框架效应下偏转转子位置控制实验。

表3 传统PID方法初始参数及优化结果

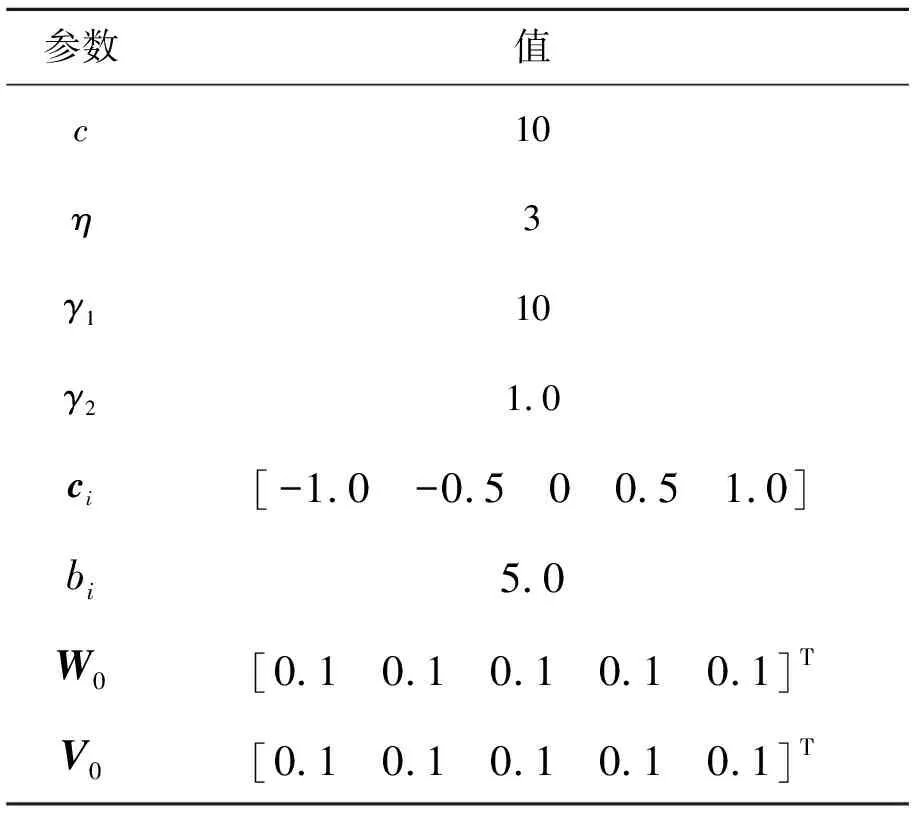
表4 神经网络滑模控制参数

4.1 径向X通道平动控制仿真

本文研究的磁悬浮CMG框架伺服系统最大设计转速为±15 (°)/s2，即最大角速率为1.632 8 rad/s，设置正弦输入为0.1sin 1.632 8tmm。其仿真结果如图8所示(彩图见期刊电子版)。图8(a)为两种控制方法对输入信号的控制效果，其中红色实线为理想位置，蓝色虚线为神经网络滑模控制方法，蓝色点线为传统PID控制方法；可以看出本文方法稳态误差更小，仅为0.000 1 mm。图8(b)为两种方法的误差对比图，红色实线为本文方法的误差，蓝色点线为传统PID方法的误差；从中可以看出本文方法的位置误差不到传统PID方法的5%。

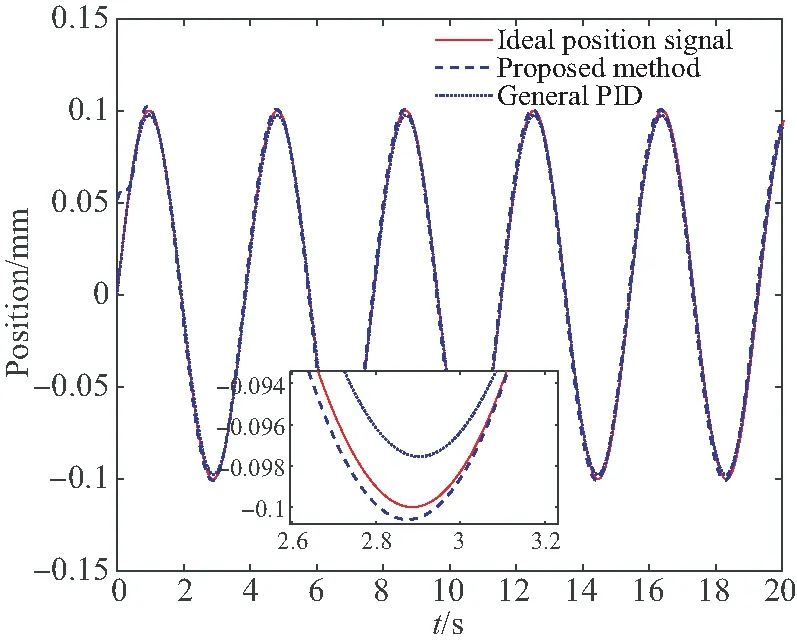
(a)两种方法的位置对比 (a)Position comparison

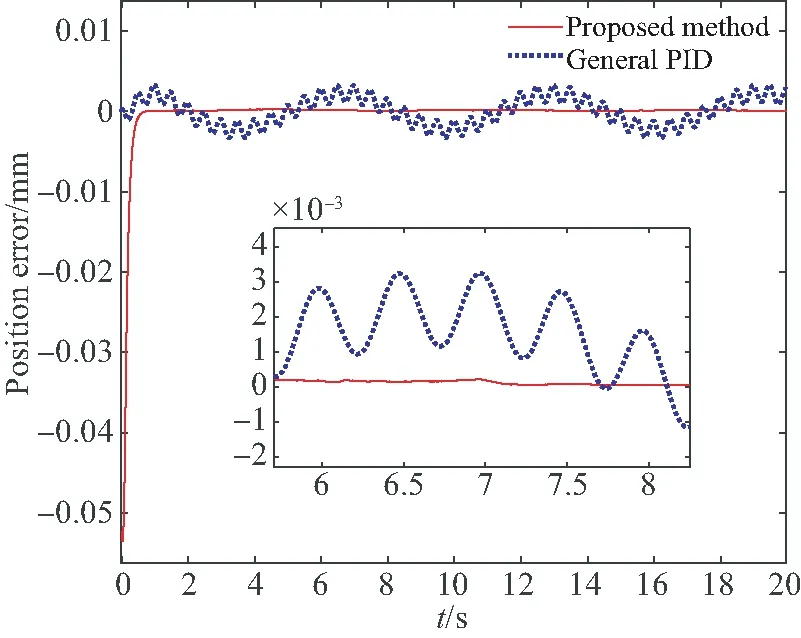
(b)位置误差对比 (b)Comparison of position error图8 转子平动方向正弦输入控制效果Fig.8 Control effect of sinusoidal input in translational direction

将转子平动方向阶跃输入设置为0.1arctan 20t，其控制位置的仿真结果如图9所示(彩图见期刊电子版)。图9(a)表示两种方法对输入信号的控制效果，其中红色实线为理想位置，蓝色虚线为神经网络滑模控制方法，蓝色点线为传统PID控制方法；本文方法的稳态误差仅为0.000 1 mm。图9(b)为两种方法的误差对比图，从中可以看出传统PID方法控制过程转子位置存在较大幅度的波动，而本文方法波动极小。

(a)两种方法位置控制效果 (a)Position comparison

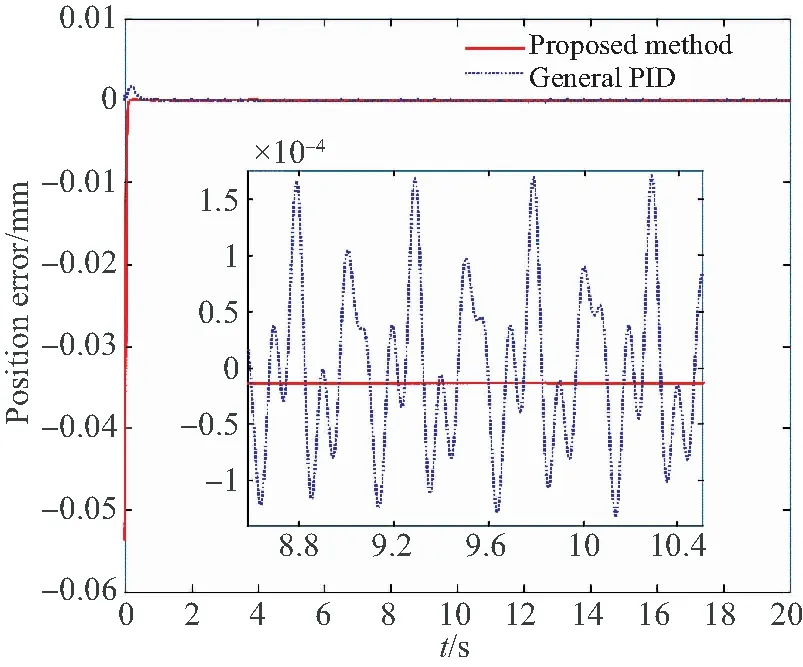
(b)位置误差对比 (b)Comparison of position error图9 转子平动方向阶跃输入控制效果Fig.9 Control effect of step input in translational direction

4.2 偏转转子位置控制仿真

为验证本方法在转子受到由框架转动及其他不确定干扰时，仍能精确控制转子，保证其稳定悬浮并输出高精度力矩，通过对比转子偏离平衡位置的位移来比较本文方法与传统方法的控制效果。

根据CMG的设计参数和实际运行情况，在仿真中加入偏转力模拟动框架效应，加入干扰力模拟实际运行过程中存在的奇数倍频和不确定扰动。干扰设定为：

d(t)=0.2sin 1.632 8t+0.1sin 1 570t+
0.05sin 4 710t+random(σ2=0.1)(N).

如图10所示。其中0.2sin 1.632 8t是使转子在径向产生偏转的干扰力，0.1sin 1 570t和0.05sin 4 710t分别是转子在额定转速15 000 r/min下的同频和三倍频不平衡振动干扰，random(σ2=0.1)是模拟实际运行过程中的随机干扰。

图10 转子所受干扰力Fig.10 Disturbance force

当输入为正弦信号时，采用本文方法和传统PID控制方法的位置控制效果如图11(a)所示(彩图见期刊电子版)，其中红色实线表示理想位置，蓝色虚线表示本文方法的控制位置，蓝色点线为传统PID的位置。图11(b)为两种方法误差对比，可以看出本文方法的位置误差仅为0.000 2 mm，是传统PID方法的0.5%，这说明本文方法在转子大角度偏转时仍能够保证位置的高精度控制。图11(c)中，红色实线和蓝色虚线分别表示X和Y两通道的控制电流随时间变化情况，可以看出本文方法控制电流波动明显小于传统方法。

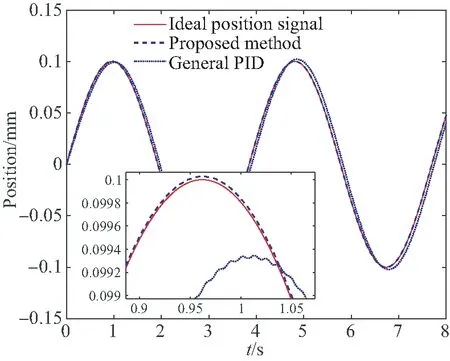
(a)两种方法的位置对比 (a)Position comparison

(b)位置误差对比 (b)Comparison of position error

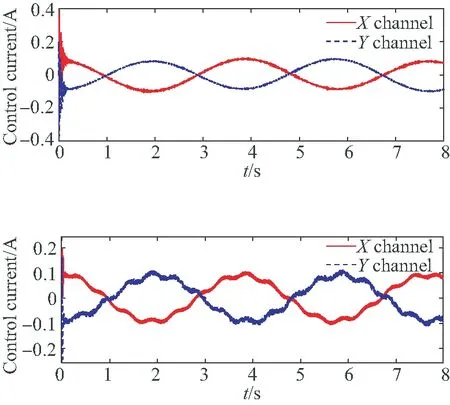
(c)本文方法和传统方法双通道控制电流 (c)Control current of proposed method and general PID method图11 双通道偏转转子正弦输入控制效果Fig.11 Control effect of sinusoidal input for tilted rotor

当输入为阶跃信号时，采用本文方法和传统PID控制方法的位置控制效果如图12(a)所示(彩图见期刊电子版)，其中红色实线表示理想位置，蓝色虚线表示本文方法的控制位置，蓝色点线为传统PID的位置。从图12(b)中可以看出，本文方法的位置误差仅为传统PID的0.125%，这说明当转子突然收到干扰时，本文方法仍能对转子进行高精度地位置控制。图12(c)中，红色和蓝色实线分别表示X和Y两通道的控制电流随时间变化情况，可以看出本文方法为保证转子位置精度，控制电流在输入信号阶跃的时刻调整频率更高。

(a)两种方法的位置对比 (a)Position comparison

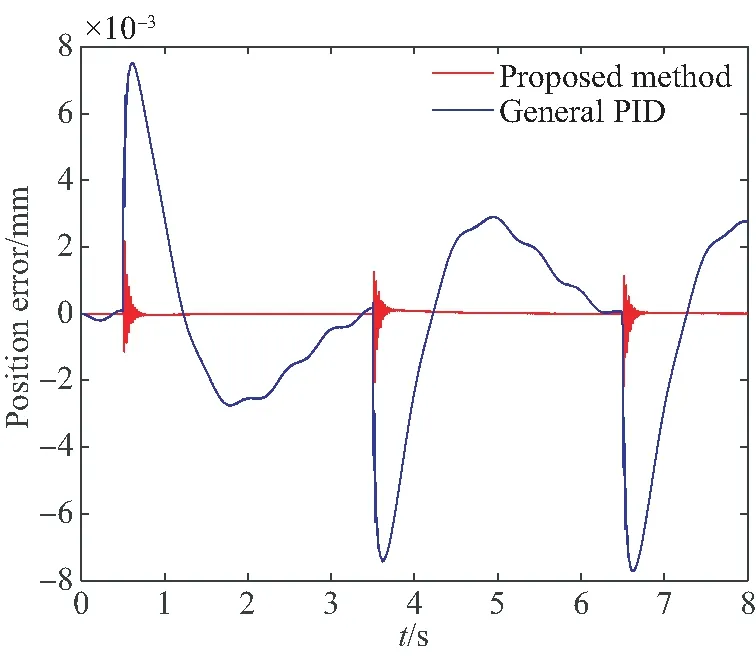
(b)位置误差对比 (b)Comparison of position error

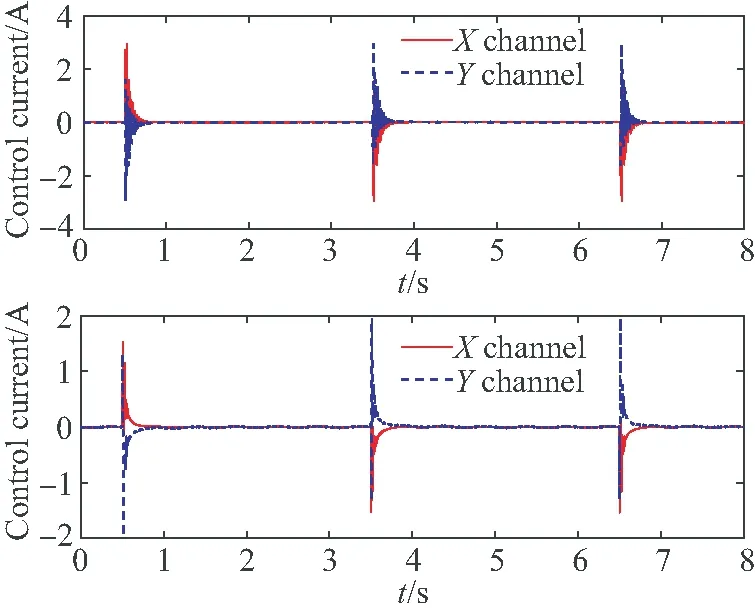
(c)本文方法和传统PID方法双通道控制电流 (c)Control current of the proposed method and general PID method图12 双通道偏转转子阶跃输入控制效果Fig.12 Control effect of step input for tilted rotor

4.2 实验验证

为了验证所提出的控制方法对提高转子位置精度的有效性，类似于仿真验证的条件，分别采用传统PID控制和神经网络滑模控制，进行径向单通道的平动控制实验。令框架转速为0 (°)/s，将转子升速至15 000 r/min。实验结果如图13所示。

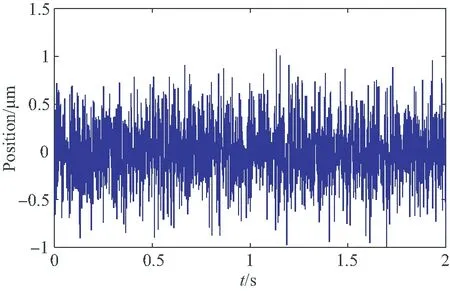
(a)传统PID控制 (a)General PID method

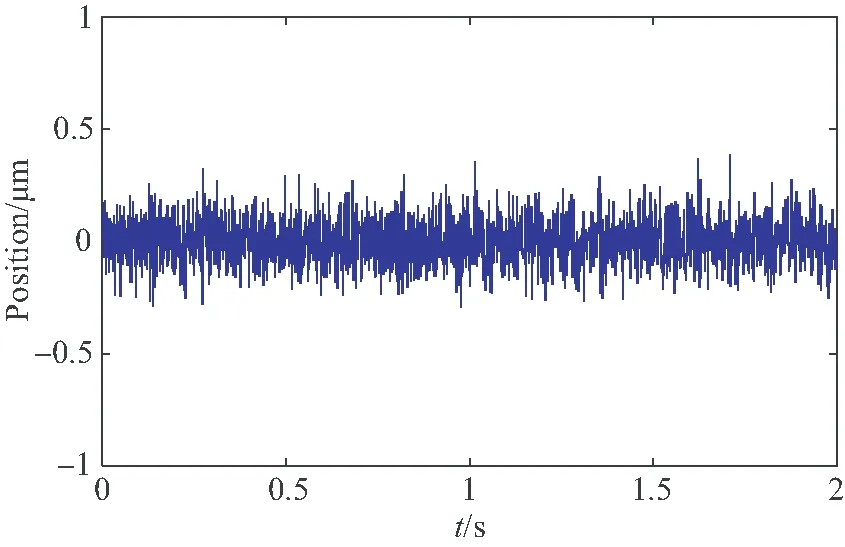
(b)所提出方法 (b)Proposed method图13 径向单通道平动控制转子位移曲线Fig.13 Position curve of the rotor in translational direction

从图13中可以看出，传统PID控制方法下，转子平动位移最大可达1 μm，而本文所提出方法转子最大位移仅为0.3 μm，位置精度比传统方法提高了70%。

为了验证框架转动情况下，转子受动框架效应而发生偏转时的位置精度，给框架系统的频率为3 Hz，幅值为10 (°)/s的正弦参考信号，两种控制方法下的转子位置精度如图14所示。从图中可以看出，动框架效应下，传统PID控制方法转子最大位移为10 μm，而本文所提方法转子最大位移为4 μm，转子位置精度提高了60%。

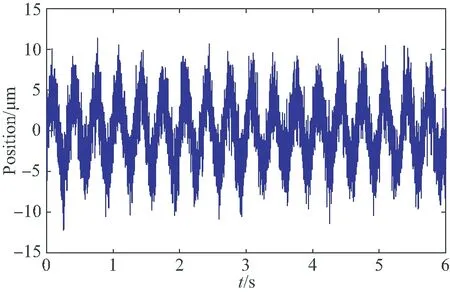
(a)传统PID控制 (a)General PID method

(b) 所提出方法 (b)Proposed method图14 动框架时偏转转子位移曲线Fig.14 Position of the tilted rotor under moving-gimbal effect

上述实验结果与仿真结果相符甚佳。然而，与仿真结果相比，在转子位移曲线中存在更加明显地高频振荡，并且实验中的位置误差更大。原因是在实际系统中还存在更多的不确定干扰和传感器噪声等因素。仿真和实验结果均验证了神经网络滑模控制方法可以有效提高MSCMG的转子位置精度。

5 结 论

磁悬浮控制力矩陀螺通过改变角动量方向输出控制力矩，具有高精度、输出力矩大等特点，能够对航天器进行高精度姿态控制。实现磁悬浮转子的高精度位置控制可以大大提高转子系统的稳定性和悬浮精度，这是磁悬浮CMG能够输出高精度控制力矩的前提之一。高速转子存在陀螺效应和不平衡振动，在干扰下更容易出现位移偏差，增加控制难度。当框架转动时，转子会较大程度偏离平衡位置，导致磁轴承间隙发生变化，这会引起位移刚度和电流刚度的非线性变化，从而使磁力发生非线性改变，降低转子位置精度，影响转子稳定悬浮，进一步影响磁悬浮CMG的输出力矩精度。

为解决上述问题，本课题针对非线性磁力模型，分析了位移刚度和电流刚度的非线性变化对磁力的影响；建立了磁悬浮转子二阶非线性不确定系统模型；设计了适用于转子径向平动控制和偏转情况下位置控制的神经网络滑模控制算法，并进行了仿真研究。在转子单通道平动控制中，与传统PID方法仿真结果对比，本文方法的稳态误差为0.000 1 mm，不到传统PID方法的5%，表明该方法有效提高了转子稳定悬浮的位置精度和抑制干扰能力；在考虑径向各通道耦合的偏转转子位置控制仿真中，与传统交叉反馈方法结果对比，本文方法稳态误差0.000 2 mm，仅为交叉反馈方法的0.125%，表明该方法能够更加有效地抑制陀螺效应，并提高转子的位置精度。实验结果表明，与传统PID方法相比，所提出方法的转子位置精度提高了60%以上。综合以上结果，证明了神经网络滑模控制能够更好地解决磁轴承系统的非线性问题。