在轨维修后端模块接口机构的研究
石 震,赵伟国,李清雅,张尧禹,杨立保*
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春 130033;2.中国科学院大学,北京 100039)
1 引 言
空间望远镜与其他航天器必须共同面临和解决在恶劣的外太空环境下复杂的航天器会出现怕各种各样的问题。而航天器本体或有效载荷因出现故障、携带的能源或能量不足、技术落后和设计功能的缺陷而不能满足当前任务,这些问题轻则造成航天器功能的下降,重则瘫痪整个航天器,导致航天器在其服务寿命内就会因为不能满足任务要求而遭到废弃,造成巨大的浪费。在轨维护可以有效地解决这个难题[1],大大延长空间科学仪器的使用寿命。
国际上在轨维护已经全面展开,早在1973年美国进行的天空实验室(Skylab)的修复是人类参与的第一次在轨维护;而在1984年的美国太阳峰年卫星(SMM)的在轨捕获,使机械臂在空间在轨操作中大放异彩[2];现在已经退役的和平号空间站(Mir)在轨服务期间前后有超过100位宇航员参与其在轨维修和升级,使其超长地完成服役期限[3];1990年发射的哈勃空间望远镜(HST)成功运用在轨操作和修复使它的寿命一直沿用至今,创造的经济效益远超初始设计的10倍之多[4];之前我国设计的空间仪器很少涉及在轨操作,大部分都是寿命一次性,如北京空间机电研究所的范斌等研究的高分五号卫星[5],长光卫星张雷等设计的某型号微纳空间遥感相机[6],长春光机所王智等研究的空间望远镜[7]。
我国在2008年发射了神州7号飞船,宇航员首次成功进行了舱外活动,这是我国航天史上的一个新的里程碑,同时也意味着我国的航天器有人在轨服务技术有了初步的基础。2016年我国成功发射了天宫二号,其中三大使命之一就是在轨维修技术试验。
本文以空间望镜后端模块在轨维修为研究对象,参照运动学原理,详细设计了一套能够满足其在轨快速拆卸和安装的接口机构。对该机构的基频和1g重力安装进行有限元仿真验证。同时为了验证该接口机构在轨的可操作性,对模块进行重力卸载,模拟了空间微重力环境,对模块进行多次重复安装。并对其进行重复定位精度测量和热应力释放各项试验验证,试验数据表明满足指标要求。
2 运动学定位原理
2.1 自由度计算
接口结构的主要任务是保证后端模块和主光机之间的正确安装,后端模块和主光机之间不能存在约束不足、过约束等问题。在后端模块正确定位的基础上再进一步设计满足支撑结构的各项技术指标,包括重复定位精度和热适应性要求。空间自由度计算公式为:
f=6(n-p-1)-pi,
(1)
式中:n为构件数目,p支撑组件的数目,pi为支撑组件约束的自由度总数。如图1所示该接口机构采用3点支撑,支撑A限制了后端模块在空间3个平动,释放了空间3个旋转自由度。支撑B限制了后端模块的y和z向的平动,释放了其他4个自由度。支撑A和B共同限制后端模块绕x和z方向的转动。支撑C限制了后端模块z方向的平动,释放其它的5个自由度,ABC三点共同作用限制了后端模块绕y轴的转动。其中ABC三点支撑分别约束了3个、2个、1个自由度,因此这种支撑简称321定位形式。在这种支撑结构中,构件一共有5个,支撑组件3个,组件约束的自由度一共为6个,带入公式(1)得f为0,321支撑共同实现了后端模块的静定支撑[8]。
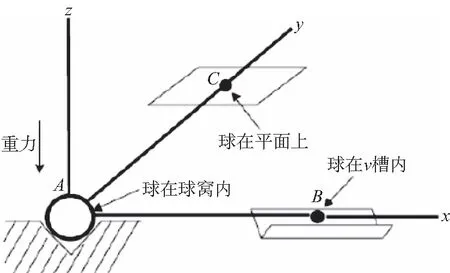
图1 定位示意图Fig.1 Schematic diagram of location
2.2 热应力释放设计原理
后端模块在太空环境工作时,工作温度和非工作温度变化大,引起的热应力和热变形通过支撑结构传递到望远镜上会导致光学系统误差增大,成像质量下降,所以接口结构设计时必须要考虑热应力释放问题。目前空间光学载荷可以分为刚性连接、柔性连接和运动学连接三种方式[9-10]。刚性连接是最简单、最直接的一种连接方式,当外界环境发生巨大温度变化时虽然可以保持很强的刚度但是它不能释放自身热应力,热稳定性差,影响最终的成像质量;柔性连接一般是铰链连接,它以牺牲自身刚度为前提,释放有限的热应力,由于存在过约束,使支撑机构的刚度较低;运动学连接的思想来自于多自由度机器人,通过解除变形方向的自由度约束可以很好地释放热应力且能保持较高的刚度。
当温度发生变化时,其中在三点锁定支撑中,若三点被完全限制,则刚体会发生整体变形如图2,三个锁紧点会发生不可控变化,而当采用运动学原理进行结构设计后如图3所示,只有A点被完全限制,则刚体会延BC轴向发生均匀变形,B点沿轴向运动,C点在xy面上运动但刚体的径向方向并没有发生变化,入射光线与靶面的相对位置不变,也就是说刚体轴向方向的变形不会对后端模块的靶面起干扰作用,温度引起的热应力和热变形通过321支撑结构的平移运动进行了释放。该接口结构原理设计简单,可靠性高,适用于高低温变化剧烈的后端模块安装,使整机在轨能够正常工作。
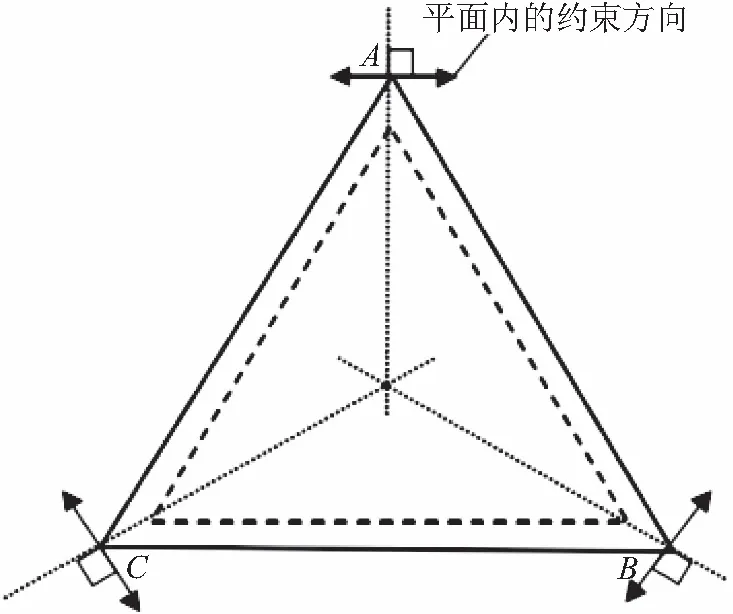
图2 三点被完全限制后的形变Fig.2 Deformation after three points limited completely
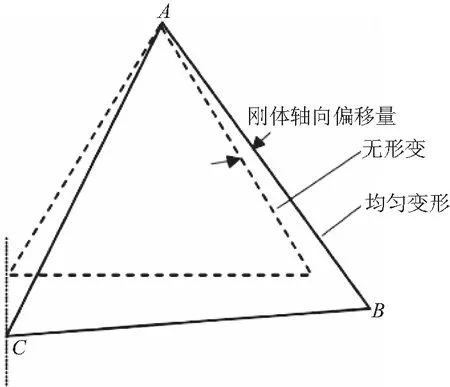
图3 采用运动学原理进行的结构设计Fig.3 Structural design using Kinematics principle
2.3 安装接口的空间布局
ABC三点均采用两端安装方式,一端安装于主光机上即不可拆卸固定端,一端安装在后端模块上即可拆卸随动端,采用整体分离方式。当后端模块推入主光机之后,通过ABC三点的完全定位实现后端模块在主光机之内的完全固定。为了保证焦平面的稳定性,安装面ABC必须保证在同一个平面内,即于入射光线垂直的平面。A点和B点由于在操作模块前需要宇航员先完成解锁操作,所以位置靠近宇航员的操作界面,C点不需要宇航员单独操作位于离操作界面的最远端。且在安装过程后,使模块相对主光机的位置保持长时间的稳定性,ABC构成三角形的中心需与整个模块的重心重合,如图4所示。
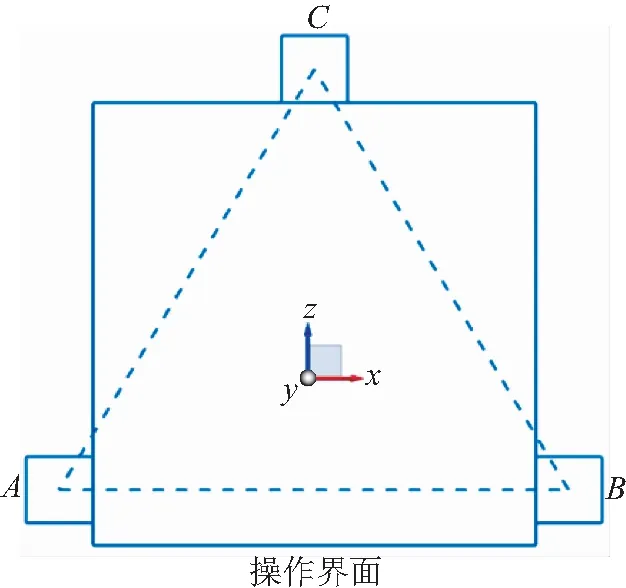
图4 接口的空间布局Fig.4 Spatial layout of interfaces
3 接口的结构设计
3.1 A点接口机构设计
A点机构形式采用典型的球头-球窝结构,这种结构的特点是限制球在球窝内三维平动自由度而释放各向的转动自由度,并集成电驱锁紧机构形成A点定位锁定点。A点机构由定位球、球窝组件、操作杆、 锁定机构和L板等组成。具体模型如图5所示,其中L板与后端模块相连,球窝组件与主光机相连。
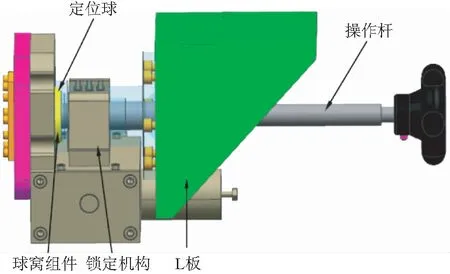
图5 A点结构图Fig.5 Structure of point A mechanism
如图5所示A点的连接可通过操作杆螺纹的旋进旋出实现紧固和分离,其中球窝组件由球窝底座和球组成,同时球在球窝内仅可自由转动而不能脱出。为了使螺杆能够准确导入球窝,特意在螺杆前端球头和螺纹之间设置一小段光杆方便导入。当欲将球头和球窝两部分固连时,可通过操作杆将L板连接的球窝与球紧密贴合形成封闭球头-球窝结构,从而在A点实现球在球窝内三维平动自由度被限制而各向转动自由度被释放的目的。对于A点3个旋转自由度并不是完全放开,通过调整球头压板与球座的间隙,使其间隙在0.02 mm,则实现A点转角限制在±0.5°范围内。
3.2 B点接口机构设计
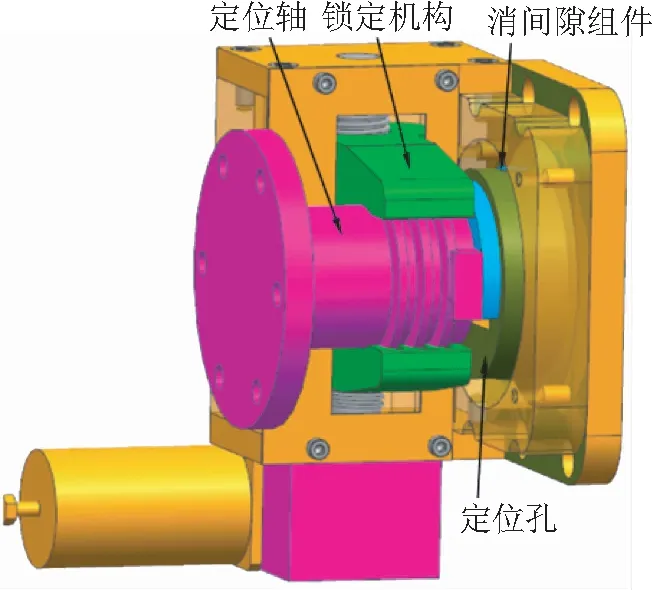
B点机构原理是典型的轴-孔结构,实现两维平动自由度的限制而释放一维平动和一维转动自度。其中轴的插拔采用了齿轮齿条结构实现了轴的横向移动,最终在后端模块固定时实现横向锁紧功能。B点机构包括定位轴套、定位轴、定位孔座、消间隙组件、锁定机构、操作杆等。如图6所示:其中定位轴套与后端模块相连,定位孔座与主光机相连。因为在重力安装条件下B点在和A点组合起到承载重力的作用,因此其对接过程需克服重力,而固连阶段有位置保持的要求,所以在B点前端设有消间隙组件。

图6 B点结构图Fig.6 Structure of point B mechanism
由于B点的设计是横向安装,在这个方向上主光机和后端模块所给的空间有限,因此在设计B点结构时要求总长度小于110 mm。由于A点的旋转自由度摆动范围只有±0.5°,所以在B点插入前会沿着AB轴线有上下摆动(图7),图8是B点前端没有锁紧之前的位置,图9是B点前端锁紧之后的位置,图10是B点前端的形状及各个参数。
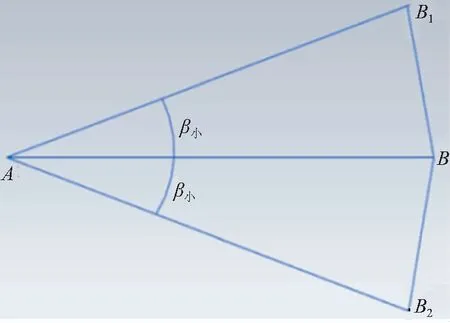
图7 B点极限转角Fig.7 B Point limit corner
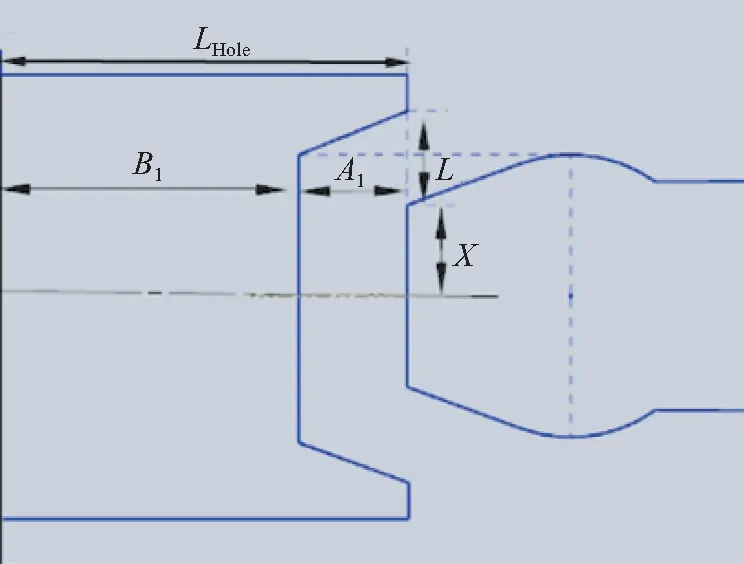
图8 B点解锁位置Fig.8 B Point unlock position
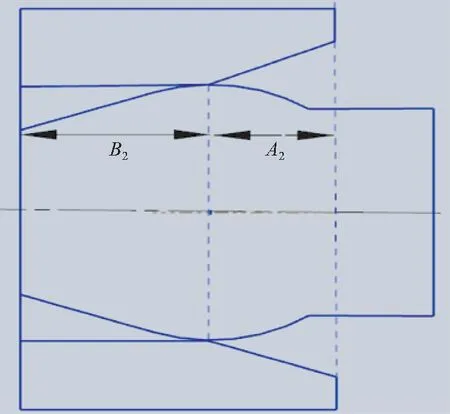
图9 B点锁紧位置Fig.9 B Point lock position
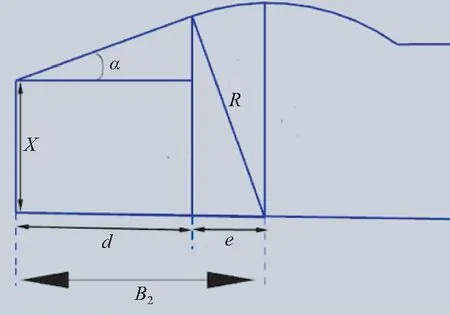
图10 B点前端参数Fig.10 B Point front-end parametersLB=L1+3LHole,
(2)
式中:LB为B点的总长度,L1代表不变量53 mm,所以LB的大小由LHole来决定。
βsmall=min{0.5,β}.
(3)
模块在A点到位之后会以A为中心旋转,本身A点的自身转角最大为0.5°,但是模块在导轨的作用下转角会有限制,定义为β,此时B点的极限转角取两个较小的一个。模块在导轨约束下的最大位移为0.4 mm,导轨一侧最远端到A点的距离为1 000 mm,可以得到A点在导轨的约束下的最大转角为
β=arctan(0.4/1 000).
B点前端移动量:
L=LABtanβsmall,
(4)
LHole=A1+B1(A1=A2,B1=B2),
(5)
(6)
(7)
孔长只和倒角α和轴的半径R有关系,取α角为15°,带入公式(5)中有LHole=17.1+0.131 6R,对于半径R通过分析可以确定式(6)~式(8)都满足A=A1=A2,B=B1=B2。
为了使倒角有一定的接触长度要求B2>10,A2>6。
(8)
可以求解出不同R下对应的X的取值的范围:
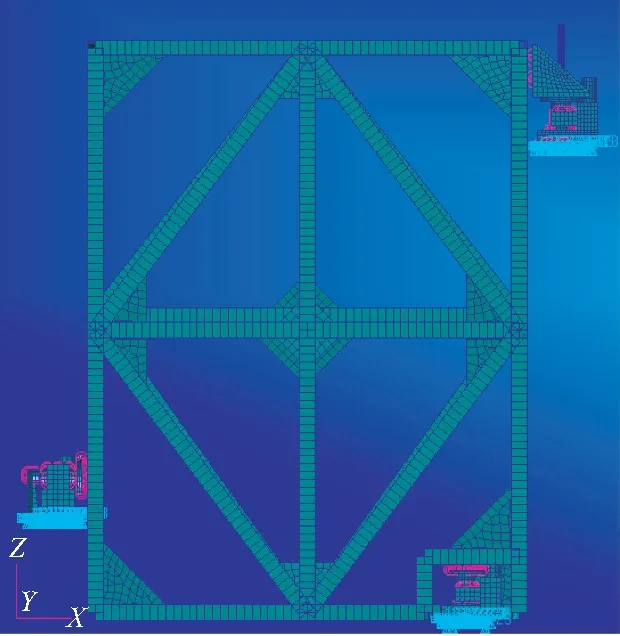
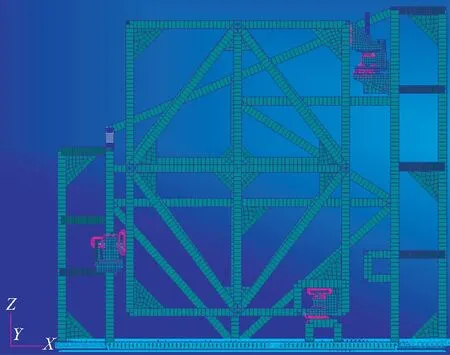
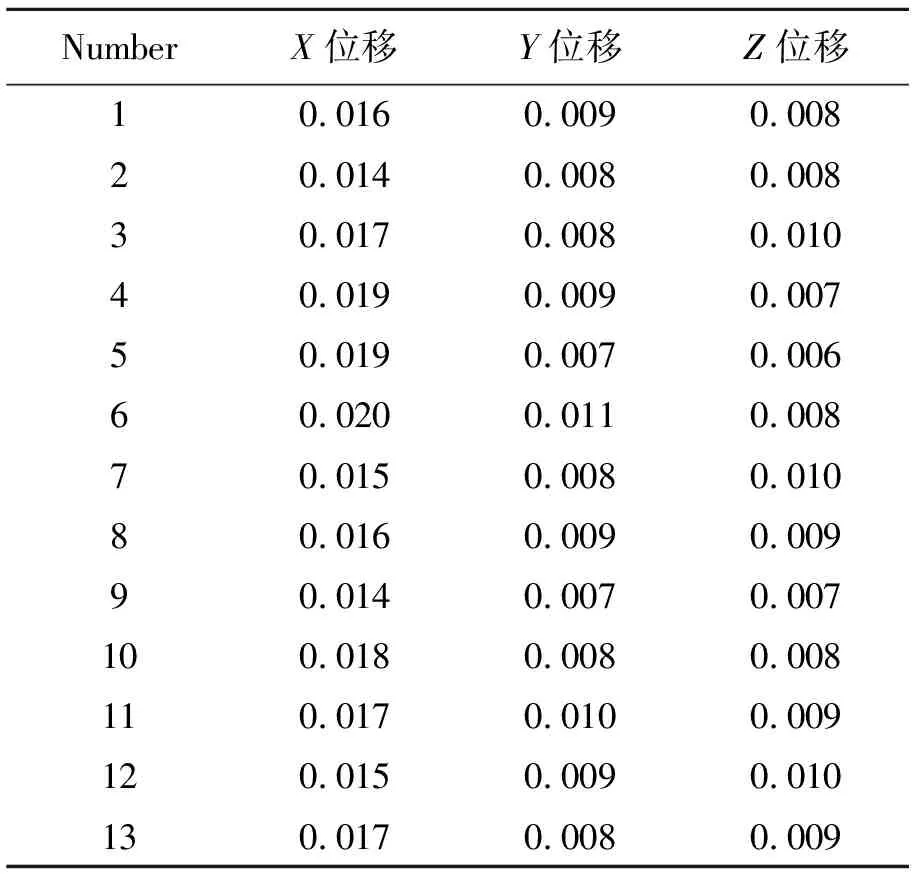
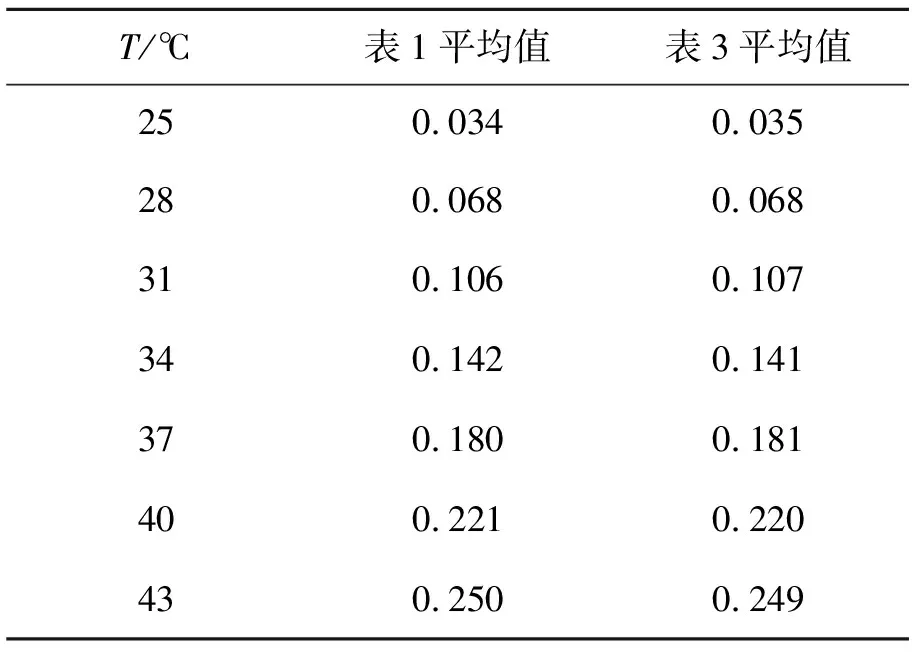
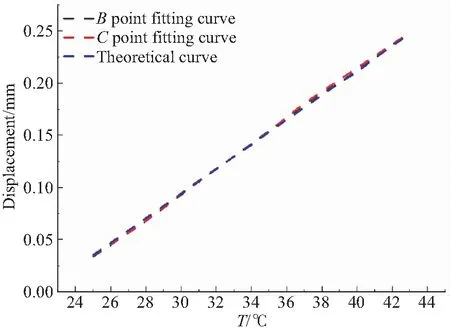
R=8.0,5.1 R=7.5,5.1 R=7.0,5.1 R=6.5,5.1 R=6.0,5.1 选取轴和孔的半径为8,给出表1以下数据。 表1 B点参数 C点机构采用的是典型的键-槽结构,作用是限定单向的自由度,同样集成了电驱锁定的机构。C点机构由定位轴、定位孔、消间隙组件及锁定机构等组成,如图11所示。 图11 C点结构图Fig.11 Structure of point C mechanism 以后端模块基频指标120 Hz为指导,对于后端模块给定杆系组合模拟。其中模块包络尺寸为1 100 mm×850 mm×340 mm,重75 kg,材料为Q235。分析时对三维模型进行了简化,形成了在轨维修接口模样件的有限元模型。ABC接口组件选用9Cr18,并将ABC结构中复杂的非承力部分以简单结构代替,并通过MPC连接形式表示相互连接关系和自由度释放,有限元模型主要采用杆单元、五面体单元、六面体单元进行划分,整个组件的有限元模型中共有12 463个单元,对接口ABC与主光机连接面进行约束,有限元模型如图12所示。结果表明一阶频率为105 Hz,远高于空间望远镜整体基频30 Hz,可以很好地避免与整体共振。 图12 有限元模型Fig.12 Finite element model 表2 结构材料各项性能指标 表3 前3阶固有频率以及各阶模态的质量参与因子 1g重力验证:由于组件在装调的过程中完全是在地表进行,此时承受自身重力的作用,而光学载荷入轨之后,处于失重状态,重力被完全卸载,就造成了天地环境载荷不一样的使用状态,为了更好地验证在轨操作可行性,验证地表装调之后不影响在轨状态,使其必须在材料弹性变化范围之内。增加与模块安装的主光机模型,同样也是使用Q235的杆系结构,模型尺寸为1 500 mm×1 290 mm×440 mm,主光机自身质量为95 kg。对模型施加1g重力,边界条件为安装状态时主光机底部进行约束。有限元分析结果显示在解锁状态最大位移是1.16E-2 mm,应力为11.7 MPa;在锁紧状态最大位移是8.16E-3 mm,应力为8.12 MPa;远小于材料的屈服强度,验证了地面装配调试环境不会影响在轨性能,使整体结构在轨释放1g重力之后完全恢复如初。 图13 静力有限元模型Fig.13 Finite element model of statics 为了验证在轨维修接口机构的可行性,加工平面工装试验件,对其进行重力卸载。可以通过两种方式验证:一种是通过气浮吊具,对装置进行重力卸载,一种是通过配重块对装置进行重力卸载[11],来模拟在轨操作的可行性。本实验采用第二种方式利用与模块等重的铅块及定滑轮,将定滑轮安装在悬吊框架上,吊丝穿过定滑轮,一端连接光学载荷模块,一端吊起铅块实现光学载荷模块的重力卸载。在轨维修可行性试验装置总体实物如图14所示。 图14 试验现场Fig.14 Laboratory scene 为了保证模块在轨维修过程中能够快速准确地安装,需要对整个模块进行多次安装与插拔,验证安装前后各点的变化量。实验采用激光跟踪仪对空间上的4个靶球的位置进行测量,精度为0.001 mm,最终获得模块上最具特征的3个点的位移。如图14所示,选取安装平台上不动靶球0作为基准点,模块上分别在紧靠接口的位置装有动靶球123,1靶球靠近A点,代表模块A点的变动量;2靶球和3靶球分别靠近BC两点,各自代表模块最远端的变动量。对模块进行反复插拔安装,测量4个靶球点的安装前后位置的变化量,即为整个模块最大的位移量。处理得出模块在3个方向的最大位移量如表4所示,根据格罗布斯准则[12],所测得的数据中不含粗大误差。 表4 3个方向的试验位移 重复定位精度: σ=3S, (9) 其中标准差S为: (10) 式中:xi是位移残差,n是测量次数把表4中的数据带入公式9和10可知x方向的平移误差为3Sx=±5.58 μm,y方向的平移误差3Sy=±3.24 μm,z方向的平移误差为3Sz=±3.63 μm,优于总体指标±10 μm。 在轨仪器最大的问题就是能适应空间高低温的变化,能更好地释放热应力和热变形。铝合金(LC9)对热变形有很高的敏感性,为模块安装板的最佳选择。其热涨系数α为23.6×10-6/℃。为了使加热连续,在模块上表面均匀粘贴8块大小相同的加热片。模块ABC三点支撑的B点释放了x方向的平动,C点释放了x和y方向的平动。在B点和C点同时分别放置两个千分表,千分表的测量精度为0.001 mm,表1为测量B点轴端的位置变化,测量沿轴向即坐标轴x方向的变化量;表2为测量B点安装面的变化量;表3为测量C点轴向即坐标轴y方向的变化量;表4为测量C点安装面的变化量。实验时的室温是22 ℃,对模块进行恒温加热并记录各个千分表的变化量,通过多次测量,获取表1和表3在各个温度下的平均值。在大量反复加热的过程中千分表2和千分表4的变化量介于0和0.001之间,认为模块的安装面没有变化。 表5 热试验结果 根据321热释放原理可知,模块以A点为不动点,B,C沿各自轴向进行热应力释放。B,C两点的位移量变化量: (11) 其中:lBA,lCA分别代表B点相对于A点在x方向的距离500 mm,和C点相对于A点在y方向的距离500 mm,带入公式可得B,C两点有共同的理论热位移: ΔL=0.011 8t-0.259 6. (12) 通过最小二乘法获得B点和C点的拟合直线: (13) 图15 热测试现场Fig.15 Thermal experiment scence 分别与理论公式进行比较: 其中:δ1为B点斜率相对理论斜率的变化率3.4%,δ2为C点斜率相对理论斜率的变化率2.5%,δ3为B点截距相对理论截距的变化率5.3%,δ4为C点截距相对理论截距的变化率3.9%;测试数据表明与理论误差率小于6%。 说明此接口机构可以很好地释放热应力,保证了焦平面的稳定性。 图16 温度位移曲线Fig.16 Temperature-displacement curve 本文以空间望镜在轨维修为研究对象,参照运动学原理,详细设计了一套能够满足其在轨快速拆卸和安装的接口机构。对该机构的基频和1g重力安装进行有限元仿真验证;后端模块基频远高于整体基频30 Hz,有效地避免了共振,证明刚度分布合理;同时为了验证该接口机构在轨的可操作性,模拟了空间微重力环境,对该机构进行多次重复安装并对其进行重复定位精度进行核算,试验数据显示3个方向的重复定位误差均优于指标±10 μm;热应力释放与理论值相对变化率优于6%;可以作为空间在轨维修接口应用,为其他在轨维修空间科学仪器提供理论参考。
3.3 C点接口机构设计
4 有限元分析
4.1 模态分析


4.2 静力学分析
5 试验验证
5.1 重力卸载

5.2 重复定位精度验证
5.3 热应力释放验证:
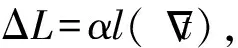

6 结 论

