电磁式电流互感器谐波特性*
李 鹤,岳长喜,邵海明,刘星余,白德进
(1. 中国电力科学研究院有限公司 计量研究所,武汉 430074; 2. 中国计量科学研究院 电磁计量科学研究所,北京 100029; 3. 北京信息科技大学 仪器科学与光电工程学院,北京 100192)
随着电力电子技术在电力系统的大量应用和新能源的大规模接入电网,非线性负荷数量越来越多,容量也越来越大[1-5].谐波大量注入电网,电力系统电压、电流波形发生严重的畸变,尤其是电流.谐波电流的监测、治理和电能计量,对谐波电流的准确测量提出了广泛的需求.大多数仪表是专门针对工频正弦波设计的,谐波有可能造成不正确的测量,导致错误的结果.对电网中电流进行测量时,作为中间桥梁的电流互感器(CT)准确变换一次畸变电流的性能至关重要[6-9].
本文针对CT的T型等效电路模型,对单一频率正弦波的误差、谐波电流误差进行分析.通过两种截然不同的试验线路和测量系统,对CT谐波误差进行了大量试验研究,揭示了误差之间的强关联性,得出了若干明确结论.本文的研究对于电网谐波电流测量设备的选型、谐波电流互感器的校准技术均具有重要的借鉴意义.
1 电流互感器研究模型
为了对CT的谐波测量特性进行试验研究,利用硅钢片铁芯制作了一个500 A/5 A电流互感器.二次绕组匝数为100匝,额定负荷为10 VA.额外绕制了100匝一次绕组,以方便采用等安匝法进行相关误差试验,由此可以显著降低对电源和测试设备的要求[10-12].与实际情况(以500 A/5 A变比运行)相比,等安匝法(以5 A/5 A变比运行)主要对磁性误差产生影响.对2 000 A/5 A与5 000 A/5 A的CT研究表明,由磁性误差带来的差异小于0.01%[13-14].由于本文研究的CT铁芯直径较小,所以受磁性误差的影响将小得多.
若已知CT铁芯的励磁、损耗特性及二次绕组的参数,可以通过公式比较精确地计算出CT的误差.将CT一次电流折算至二次侧,且一次、二次绕组匝数相等,则CT的T型等效电路如图1所示.

图1 CT的T型等效电路Fig.1 T-type equivalent circuit of CT
图1中的符号含义如下:I′1为折算至二次侧的一次电流相量;I2为二次电流相量;I0为用于铁芯激磁的电流相量;R′1为折算至二次侧的一次绕组内阻;L′1为折算至二次侧的一次绕组漏感;R2为二次绕组内阻;L2为二次绕组漏感;Rm为铁芯激磁损耗等效电阻;Lm为铁芯激磁等效电感;ZL为CT的负载阻抗.其中,二次绕组漏感L2在大部分研究中均忽略不计.根据Gamilli等学者[15]对不同CT的试验研究可知,300A/5ACT的二次绕组漏感约为5μH.若漏感与绕组匝数的平方成正比,本文中的试验CT二次绕组漏感可估算为14μH.在1 000Hz下,电抗约为0.09Ω,相对于其他参数,可忽略不计.由图1容易得到如图2所示的相量图,其中,E为二次绕组感应电势.
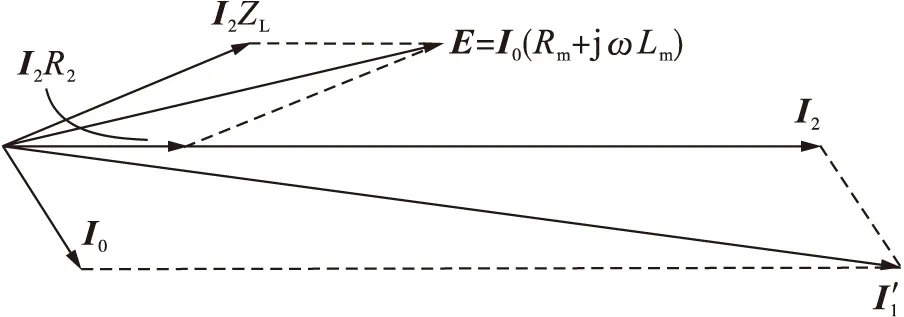
图2 CT的相量图Fig.2 Phasor diagram of CT
定义相量I2和I′1的幅值差异为CT的比值差,I2超前于I′1的角度为CT的相位差.为简单起见,假设负载为纯阻性,用RL表示,可推导CT的比值差和相位差为
(1)
(2)
当CT通过较长的电缆连接至测量设备时,必须考虑由于电缆电容所带来的误差,其等效于在图1所示电路的负载ZL两端并联一个电容,该电容中流过的电流并未流过负载,所以会造成误差.以本文试验的感性负载为例,电感L=0.48mH,电阻R=0.37Ω.在2 000Hz下,其阻抗达到了6Ω.当二次电流为1A时,负载上的压降为6V.假设电缆电容为3nF(约等于80~100m长双绞线间的电容),该电容间的泄露电流为0.23mA,因此,在2 000Hz下电缆电容约造成0.023%的误差;在1 000Hz下,该误差降低至0.006%.在本文的研究中,二次电缆长度较短,故等效电路忽略了该电容.
2 CT对单一频率正弦波的误差研究
由图1可见,CT存在误差的原因是铁芯需要消耗激磁电流I0.若能够得到激磁阻抗的参数Lm和Rm,即可从理论上计算出CT的误差,然而这两个参数均受到激磁频率、铁芯磁密水平的影响,不是常量.Douglass曾利用电流频率f的平方根来修正激磁阻抗模型[16],但该模型误差较大,不能用于精确地分析误差.
本文通过如下方式间接测量铁芯的激磁参数:试验CT的二次绕组内阻R2经实测为0.17Ω,纯阻性负载ZL=0.4Ω.当CT一次电流分别为20%和100%额定时,二次绕组的感应电势分别为0.57和2.85V.
将试验CT二次绕组开路,对CT的一次绕组施加不同频率的激励电流Ie,使二次绕组的感应电压分别为0.57和2.85V.测量此时激励电流大小及其与感应电压Ue之间的相位关系,即可计算出不同频率、不同磁密水平下的激磁参数.该试验的等效电路如图3所示.图3中,RS为激励电流的采样电阻(高准确度无感电阻).

图3 CT激磁参数的测量Fig.3 Measurement of magnetizing parameters of CT
利用测得的激磁参数,根据式(1)、(2)计算CT在纯阻性负载下,各激磁参数及单次正弦波电流的误差如表1所示.

表1 激磁参数测量结果及计算误差Tab.1 Measurement results of magnetizing parameters and calculation errors
为了验证表1中的计算误差,必须对误差进行实际测量.本文利用图4所示宽频自校准线路测量试验CT在50~2 000 Hz电流下的误差.

图4 CT的宽频自校准电路Fig.4 Wide band self-calibration circuit of CT
图4中参考电阻和差流电阻上分别流过一次电流I1与误差电流I2-I1,其分别产生电压相量UR和ΔU.利用锁相放大器测量ΔU相对于UR的大小与相位,进而可计算出CT的误差.
分别对纯阻性负载和带感性的负载(50Hz时功率因数为0.92)进行试验.感性分量采用漆包线制成的线圈,这样可以保证负载电感在试验电流频率范围内不会发生较大的变动.在50Hz频率下,两者的阻抗均为0.4Ω,试验数据如表2所示.

表2 宽频校准试验数据Tab.2 Test data by wide-band calibration
对比表1、2的计算误差及实测误差,可以证明本算法取得了良好的一致性.比差最大差异为0.017%,角差最大差异为0.4′.利用图3所示电路测量激磁参数,可计算CT的误差,而图2所示宽频自校准电路及相应测量系统的有效性也得到了间接验证.
根据等安匝法原理,试验CT的5 A/5 A变比和500 A/5 A变比的误差应保持一致.利用传统校验仪对500 A/5 A变比在50 Hz电流下的误差进行测量,结果如表3所示.

表3 传统方法的500 A/5 A校准数据Tab.3 Calibration data of 500 A/5 A with traditional method
在50 Hz电流下,该CT满足0.2级的要求.虽变比不同且测量方法不同,但比差与角差的最大差异分别为0.03%和1.1′,约为0.2级互感器误差限值的1/10,该种差异可能是由于CT自身的稳定性及测量方法的不同所带来的,亦或是在试验时并未将负载控制得完全相等的缘故.但较小的差异证明了利用图4所示自校线路在小电流下研究CT误差特性的有效性.
进一步分析表2数据可知,对于纯阻性负载,随着一次电流频率的增大,CT误差会逐渐减小.这是因为对于相同幅值、不同频率的被测电流而言,二次绕组的感应电压几乎不变.而频率越高,用于铁芯激磁的电流越小,因而误差也越小.对于感性负载而言,高于1 000 Hz后,二次绕组的感应电压成倍的增大,铁芯中的励磁电流也将增大,最终造成误差增大,尤其是角差增大趋势明显.为了准确地将宽频率一次电流变换为二次电流,采用低阻值的纯阻性负载是有必要的.对于感性负载(功率因数不低于0.9),CT对2 000 Hz以下的正弦波电流仍具有较好的响应,保守估计其准确度不会降低两个等级以上.
3 CT对谐波电流的误差研究
为了研究CT对谐波电流的测量特性,搭建了如图5所示的测量平台.
信号发生器产生了基波电压Ufsinωt及n次谐波电压Uhsin(nωt+φ).在加法器上叠加产生谐波电压,通过功率放大器升流器产生谐波电流If1+Ih1,进而试验CT产生二次电流If2+Ih2.基波与谐波之间的相角φ可以在信号发生器上设置.CT的二次阻抗ZR用于调整CT负载阻抗至阻性或感性的设定值,与前述试验的负载条件保持一致.

图5 CT的谐波误差测量平台Fig.5 Measurement platform for harmonic error of CT
在不同的条件下,进行了大量的基波、谐波电流误差测量试验,试验步骤归纳如下:
1) 设定一次基波电流为1A,谐波电流大小为0.2A,频率为100Hz,谐波电流与基波电流的相角差为0°,二次负载为0.4Ω阻性负载,CT二次电流对一次电流的比差与角差,分别在50 和100Hz下进行测量;
2) 改变一次基波电流至5A,谐波电流大小至1A,重复步骤1);
3) 依次调整谐波电流和基波电流的相角差至45°、90°,…,315°,重复步骤1)和2);
4) 依次更改谐波电流频率为150、200、400、1 000Hz,重复步骤1)~3);
5) 改变二次负载为0.4Ω感性负载(功率因数在50Hz下为0.92),重复步骤1)~4).
为了将问题简单化,首先来分析谐波相角对基波和谐波电流误差的影响,然后将不同谐波相角下的误差取平均值,评估谐波电流对CT误差的影响.
3.1 谐波相角对误差的影响
由于数据较多,应进行适当的分类.每个误差数据由以下几个维度决定:1)一次电流大小;2)负载特征;3)谐波电流频率;4)比差或是角差;5)谐波相角.依据前4个维度对数据进行分组,并求取每一组数据的试验标准偏差,得到由前4个维度确定的数据组.该试验标准偏差代表了谐波相角对基波和谐波电流误差的影响.
进一步依据维度3)和4)对数据进行分组,对每一组的试验标准偏差取极大值,简化掉维度1)和2),简化后得到的数据如表4所示.

表4 由谐波相角引起的误差标准偏差Tab.4 Standard deviation of errors caused by harmonic phase angle
当谐波电流频率为400及1000 Hz时,由基波和谐波相角引起的标准偏差均极小.由此表明在较高的频率段,谐波相角几乎不对基波电流或谐波电流的误差产生影响.谐波电流频率在100及200 Hz以下时,标准偏差略大,但相对于其准确度等级对应的误差限值,也可以忽略.
谐波频率为150 Hz时,标准偏差最大.该影响显然是由于铁芯的非线性和激磁电流中含有一定量的三次谐波所造成的.宽频试验研究表明,试验CT对50 Hz电流满足0.2级,对50 Hz以上正弦波电流满足0.5级.由表4可见,在150 Hz谐波电流频率下,由谐波相角引起的误差标准偏差均约等于相应等级误差限值的1/10.总体而言,谐波相角对基波电流及谐波电流的误差影响均较小.
3.2 谐波电流对误差的影响
取一次基波电流为5 A、谐波电流为1 A、负载为纯阻性负载的数据,并将各谐波相位角的误差取平均值.与表2中的相应误差进行对比,基波电流误差及谐波电流误差如表5、6所示.

表5 基波电流误差Tab.5 Fundamental current errors

表6 各次谐波电流误差Tab.6 Current errors of different harmonic orders
由表5中数据可知,谐波电流对基波误差影响较小,比差最大变化为0.04%,角差最大变化约0.5′,比差变化略大,约为0.2级误差限值的1/5.
表6为CT对各次谐波电流的误差.各频率谐波电流误差与相应频率5 A正弦波电流的误差更接近.由于CT的误差主要取决于铁芯的磁导率,而铁芯磁密越高,磁导率则越大.谐波电流中的大幅基波分量提升了铁芯中的磁密水平,使得谐波电流的误差发生了变化.
4 结 论
本文基于等安匝法,通过几种试验方法对CT的谐波误差特性进行了大量研究.试验结果得到了交叉验证,得出如下重要结论:
1) CT对谐波电流的误差可通过对单频率正弦波电流的误差来间接表征;
2) 20%以下的谐波电流对基波电流的误差影响可以忽略不计;
3) 在基波电流的影响下,谐波电流的误差比相应幅值单次正弦波电流偏小;
4) 对于一般电磁式电流互感器而言,若对精度要求较低(1%以下),可以认为CT二次电流能较为精确地还原畸变的一次电流;
5) 为了更准确地变换谐波电流,宜选用二次绕组内阻较小的电流互感器,且尽量在CT的二次侧接入低阻性负载,并考虑二次电缆间电容对误差的影响.

