“统计和概率的简单应用”易错点例析
沈晶晶

一、简单随机抽样调查必须使样本具有代表性。不能偏向总体中的某些个体
例1为创建文明城市,太原市政府提出“创建文明城市,共建美好家园”的号召。学校为了解全体学生(共1000名,每班30人左右)对“创城”知识的掌握情况,让小颖设计抽样的方式,其中最合适的是(
)。
A.从全校的每个班级中抽取学号为5、15和25的学生进行调查
B.在七年级学生中随机抽取一个班级进行调查
C.在学校操场随机抽取10名学生进行调查
D.从学校的男同学中随机抽取50名学生进行调查
【错解】B、C、D。
【分析】简单随机抽样是否恰当,主要看三个方面:(1)样本是否具有代表性;(2)样本是否具有广泛性;(3)样本是否具有随机性。这是抽样调查中必须注意的关键点,否则就会得到不恰当的结论,失去调查应有的价值。B、C、D选项样本虽然有随机性,但本题调查对象的全体是学校1000名学生,学校除了七年级还有其他年级,除了男生还有女生,C选项中只抽取10名学生,样本容量太小了,不具有广泛性。
【正解】A。
二、概率不是频率,可能性不能等同于确定性
例2下列叙述不正确的是(
)。
A.掷一枚骰子,向上的一面出现的点数为4是随机事件
B.某种彩票中奖的概率为1%,那么买100张这种彩票一定会中奖
C.某兴趣小组14名同学中至少有两人的生日在同一月份是必然事件
D.在相同条件下,试验的次数足够大时,某一随机事件发生的频率会稳定于某一数值
【错解】A、C、D。
【分析】事件的概率是一个确定的数值(唯一的),而频率是不确定的(不唯一的)。对同一个试验而言,频率的大小波动与试验的次数有关。在大量重复试验中,如果事件A发生的频率会稳定在某个常数的附近,那么这个常数就叫做这个随机事件A的概率。可见,频率和概率在试验中可以非常接近,但不一定相等,两者存在一定的差异是正常的。当试验的次数足够大时,该事件发生的频率就会稳定在事件发生的概率附近,频率接近于理论概率。因此,我们可以用大量重复试验中事件发生的频率稳定值来估计这一事件发生的概率。
【正解】B。
三、计算概率的前提是随机事件的发生具有等可能性
例3抛掷两枚质地均匀的硬币,出现一正一反的概率是_____。
【错解】1/3。
【分析】抛掷两枚质地均匀的硬币,有些同学误认为只有三种结果:正正、正反、反反,但这三种结果不是等可能性的。实际上,两枚硬币是不同的个体,我们可以叫做硬币甲和硬币乙,所以这个随机事件出现的等可能结果有四种情况:甲正乙正、甲正乙反、甲反乙正、甲反乙反。
【正解】1/2。
【点评】在计算概率时,我们一定要判断随机事件的发生是否具有等可能性,若不具有等可能性,要设法将不等可能事件转化为等可能事件,再运用计算等可能事件概率的方法进行计算。
四、用列举法求概率时要注意区分放回试验与不放回试验
例4在一个不透明的盒子中装有4张卡片,4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀。
(1)从盒子中任意抽取一张卡片,恰好抽到标有奇数卡片的概率是______;
(2)从盒子中任意抽取2张卡片,2张卡片標有数字之和大于4的概率。(请用画树状图或列表等方法求解。)
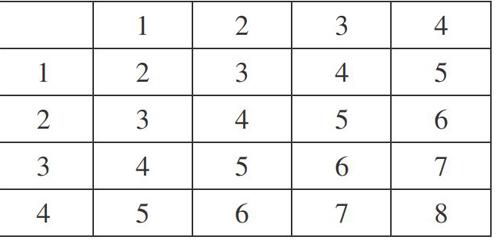
(2)根据题意列表得:
由表可知,抽取的2张卡片标有数字之禾口大于4的概率为10/16=5/8。
【分析】(1)直接利用概率公式,计算即可。抽到标有奇数卡片可能出现的结果数为2,所有可能出现的结果数为4。
(2)任意抽取两张卡片时,不能抽取两张标有数字一样的卡片,等同于“无放回”。
由表可知,抽取的2张卡片标有数字之和大于4的概率为8/12-2/3。
【点评】简单的随机事件可以直接用列举法展示所有等可能的结果,复杂一点的随机事件可以借助列表或画树状图展示所有等可能的结果。列表法适用于两步完成的事件,而画树状图法适合于两步及以上完成的事件。
- 初中生世界·九年级的其它文章
- 黄钟大吕振聋发聩
- 先生王斗造门而欲见齐宣王
- 蝶恋花
- 鹧鸪天
- 欣赏意境之美拓展想象空间
- 读书感言

