“统计和概率的简单应用”那些事儿
杨广清 王小琪

数据是蕴涵信息的,收集、整理、描述、分析数据有助于我们从数据中获取信息。而生活中的数据是海量的,因此我们有必要从中选取具有代表性的信息,帮助我们做出正确的估计、推断、决策,解决日常生活中的一些问题。
本章内容共有6节,前3节是统计部分的应用,后3节是概率方面的应用。我们之前已经了解了统计和概率的相关知识,然后便可以运用所学的知识来解决生活中的问题,从而更好地认识世界。
统计调查是数据的采集过程,统计整理是对统计调查获得的资料进行加工整理、汇总列表,使之符合当前统计研究目的的需要。这不仅仅是对统计数据进行整理、描述、分析,还需要我们做一些简单的估计推算工作。下面就按照每一节的内容来说说“统计和概率的简单应用”那些事儿。
一、中学生的视力情况调查
这一节知识我们需要掌握两项内容:一是要知道普查的局限性和抽样调查的必要性,抽样调查的样本要有代表性和普遍性;二是学会用抽样调查的结果即样本来估计总体的情况,正因为需要用样本估计总体,进而影响决策,因此要求抽样调查的样本具有代表性。
例1为确定本市七、八、九年级校服的尺寸,有关部门准备对8000名初中男生的身高做调查,现有3种方案:
(1)测量体校中200名男子篮球、排球队员的身高;
(2)查阅有关外地200名男生身高的统计资料;
(3)在市区和郊区各选4所初中,在这8所学校的所有年级(1)班中,用抽签的办法选出15名男生,然后测量他们的身高。
为了达到估计本市初中3个年级男生身高分布的目的,你认为上述哪种调查方案合理。
【解析】本题中,方案(1)体校男子篮球、排球队员身高往往高于一般学生,样本选取比较特殊,不具有代表性;方案(2)外地学生的身高由于地域或生活条件的差异,也不能准确反映本地学生的身高情况;方案(3)的抽样方法符合随机的原则,而且考虑到了年级、城郊的区别,样本中个体的数目比较合适,样本具有代表性。
【点评】要判断一个样本相对总体是否具有代表性,一看样本调查范围的大小,一般来说,范围小不具有代表陛;二看样本是否具有普遍性,是否能反映总体的一般情况;三看抽样是不是随机的。
二、货比三家
这一节知识在生活中经常用到。生活中我们会遇到很多数据,从中能够获得许多有用的信息,但有些信息不一定全面、客观,需要从不同的角度观察、分析数据,感受数据对于决策的重要性,进而全面综合考虑各个因素,“货比三家”。
为了吸引零售超市到某个地方来营业,如果这样介绍:这个地方居民的平均收入非常高。看到这个,就以为这个地方的大多数居民都属于高收入阶层,那就有可能是不正确的。如果有一个亿万富翁恰好住在该地方,其他人可能是一般收入人群,而该地区平均收入却仍然很高。
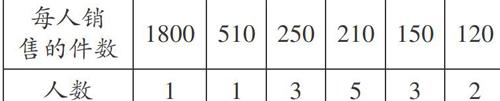
例2某公司销售部有人员15人,销售部为了制定某种商品的月销售任务,统计了这15人某月的销售量如下表:
如果把平均月销售额作为他们的销售任务,这样的平均合理吗?
【点评】“平均”这个词往往是“算术平均值”的简称,这是一个很有用的统计学的度量指标。平均数绝大部分时候能反映客观情况,但容易受到极端值的影响,从而造成“平均数不平均”的现象。如工厂中有少数高薪者,“平均”工资就会给人错误的印象。再如,某公司招聘员工,从15名应聘者中取笔试成绩前8名进入下一轮,那如果要判断是否进入下一轮,应聘者只需要用自己的成绩与15个成绩的中位数(第8名)对比即可。因此我们应根据实际需要,选取合适的角度观察分析数据。
三、统计分析帮你做预测
在这一节,我们感受到用函数图像可以大致判断事物的发展趋势,进一步体会到统计与预测之间的关系。如在日常生活中,學生的身高和体重之间存在着某种关系,这样的关系不一定完全贴合函数的图像,可能是近似地体现变化趋势,但是借助这样的变化趋势,我们同样可以预测一些结果,更好地服务于生活。
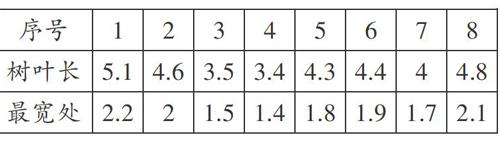
例3小明随机调查了某种树的树叶长(cm)与最宽处的宽度(cm),整理如下:
(1)以最宽处为横坐标,树叶长为纵坐标,在平面直角坐标系中画出对应的点,并选用适当的直线近似地表示它们之间的变化趋势;
(2)求这种树叶的树叶长与最宽处之间关系的表达式,并估计当最宽处是3cm的时候,树叶长度是多少?
【解析】在平面直角坐标系里画出它们对应的点,发现图像可以近似地看成一条直线。恰当地选取两个点作一条直线,并尽量使其他的点在这条直线附近,从而求出函数表达式,进而根据自变量的取值,得出对应的函数值。
【点评】通过样本对总体进行估计,在生活中还有很多类似的例子。我们常常用统计知识发现两个量之间存在着一定的关系,从而进行预测,帮助我们做出决策。
四、抽签方法合理吗
这一节主要讲抽签在生活中应用的合理性。很多时候用抽签的方法决定某件事情,比如用抽签决定谁去参加比赛,那么先抽的人和后抽的人中签的概率一样吗?概率论的兴起,本来是由保险事业的发展而产生起来的,但刺激数学家思考概率论问题的却来自赌博者的请求。惠更斯的《论赌博中的计算》,是概率论最早的一部著作。华蘅芳与傅兰雅合译的《决疑数学》是最早介绍到我国的概率论著作。概率论现在已经成了数学的一个重要分支,在科学技术的各个领域里都有着十分广泛的应用。
例4为决定谁获得仅有的一张电影票,甲和乙设计了如下游戏:在三张完全相同的卡片上,分别写上字母A、B、B,背面朝上,每次活动洗匀。
甲说:我随机抽一张,抽到字母B,电影票归我;
乙说:我随机抽一张后放回,再随机抽一张,若两次抽到的字母相同,电影票归我。
(1)求甲获得电影票的概率;(2)求乙获得电影票的概率;(3)这个游戏公平吗?
【解析】(1)甲获得电影票的概率是2/3;(2)利用树状图或表格,容易得出共有9种可能的结果,它们的出现是等可能的,两次抽到的字母相同的结果有5种,因而乙获得电影票的概率是5/9;(3)甲、乙获得电影票的概率不相等,这个游戏不公平。
【点评】游戏公不公平取决于这两个事件发生的概率是否相等,而非等于1/2。乙获得电影票这个事件是有放回的抽取,因而第二次抽取不受第一次影响,在画树状图或列表格时,需要关注第一次抽的卡片,第二次仍可以被抽到。若出现“无放回”或“随机抽取两个”,这个事件就属于无放回抽取,第一次抽到的卡片,第二次是抽不到的。
五、概率帮你做估计
这一节我们主要学习如何估计某个种群的数量,比如估计鱼塘中鱼的数量等。在进行估计的时候常采用“捉放捉”的方法,即先捕捉鱼若干条,做上记号,然后放归,过段时间后,重新捕捉,通过计算捕捉的鱼的数量及带记号的数量,从而估计出鱼塘中鱼的条数。
例5在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验.之后把它放回袋中,搅匀后,再继续摸出一球。以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
根据列表,可以估计出n的值是____。
【解析】通过表格得出摸出黑球的概率随着试验次数的增多,逐渐稳定在某个值的附近。经过大量的试验得到摸出黑球的频率的估计值是1/2,我们就用这个频率去估计概率,再由n个小球中有5个黑球,可估计得n的值是10。
【点评】每个对象出现的次数与总次数的比值称为频率,大量重复试验所得到的随机事件发生的实际频率接近于该事件发生的理论概率,我们常常用大量重复试验的频率去估计理论概率。还有一些事件,从理论上看,比较难以得出概率,我们也可以用频率来估计概率。
六、收取多少保险费才合理
这一节内容主要是进一步理解事件发生的频率与概率之间的关系,会利用概率计算随机事件发生的平均次数,体会概率在生活中特别是保险业中的应用。
首先要理解事件发生的平均次数,一般地,如果随机事件A发生的概率是P(A),那么在相同的条件下重复n次试验,事件4发生的次数的平均值m为nxP(A)。
例6人寿保险公司的一张关于某地区的生命表的部分摘录如下:
(1)某人今年50岁,他当年去世的概率是多少(精确到0.001);
(2)如果有20000个50岁的人参加人寿保险,当年死亡的人均赔偿金为10万元,预计保险公司需赔偿的总额为多少?
【解析】50歲当年去世的概率,用50岁去世的人数除以50岁的总人数,得:=0.012;用这个概率估计20000个50岁的人去世的概率,估计出这20000个人里面当年去世的人数,从而求出赔偿总额,20000x0.012x10=2400万。
【点评】我们应在保险业的背景下理解平均次数、平均值的概念,比如某事件发生的概率为0.3,不是每10次必有3次发生,而是在大量重复试验下,平均每10次大约发生3次。
(作者单位:江苏省仪征市教学研究室,江苏省仪征市实验中学东区校)
- 初中生世界·九年级的其它文章
- 黄钟大吕振聋发聩
- 先生王斗造门而欲见齐宣王
- 蝶恋花
- 鹧鸪天
- 欣赏意境之美拓展想象空间
- 读书感言

