纬编针织物导热性能的有限元仿真

杨恩惠 初曦 邱华

摘要： 为了提出一种用于优化、评估、预测针织物导热性能的方法，文章探索了纬编针织物热量传递的有限元仿真模拟，尤其是夏季汗衫面料，因为其导热性能与人体舒适性密切相关。首先使用织物厚度仪和超景深显微镜获取织物结构参数，通过插入三次B样条曲线建立纬平针织物的三维几何模型。然后将单元线圈模型导入有限元分析软件STARCCM+中，通过网格划分、边界设置、迭代计算步骤进行数值计算，并和实验值进行了比较分析，误差在4%以内。表明此方法具有一定的实用性，可用于预测纬编针织物的导热性能。

关键词： 纬编针织物;导热性能;三维模型;有限元仿真;网格划分

中图分类号： TS186.2文献标志码： A文章编号： 10017003（2020）01003106

引用页码： 011106DOI： 10.3969/j.issn.10017003.2020.01.006

Finite element simulation of thermal conductivity of the weft knitted fabric

YANG Enhui， CHU Xi， QIU Hua

Abstract： In order to propose a method for optimizing， evaluating and predicting the thermal conductivity of knitted fabrics， the finite element simulation of heat transfer of weft knitted fabrics was explored in this paper. Especially for summer Tshirt fabric， its thermal conductivity is closely related to the comfort of human body. Firstly， fabric structure parameters were obtained by means of fabric thickness meter and ultradepthoffield microscope. And threedimensional geometric model of weftflat knitted fabric was established by inserting cubic Bspline curve. Then， the element loop model was imported into the finite element analysis software STARCCM+. The numerical calculation was carried out by mesh division， boundary setting， and iterative calculation steps. Compared with the experimental data， the error was less than 4%. It is shown that this method is practical and can be used to predict the thermal conductivity of weft knitted fabrics.

Key words： weft knitted fabric; thermal conductivity; threedimensional model; finite element simulation; mesh division

服装织物的热舒适性一般指人体在不同环境条件下或者不同活动条件下，外界环境与内在皮肤产生热量的交换，达到平衡时使人感到舒适的特性。实验条件下，衡量织物热舒适性能的指标一般采用克罗值、热阻或传热系数等[1]。

在研究织物热传导的过程中，以往大多研究其影响因素，宋兰霞等[2]测试不同经纬密的织物来研究结构密度、厚度、含气量对织物导热性能的影响;吴海军等[3]选择不同组织结构的织物，利用线性分析织物厚度、平均浮长、覆盖系数对织物热传递性能的影响。刘让同等[4]采用织物叠加的方式探讨厚度、容重等对热阻的影响，建立了拟合回归曲线，其二者组合参数时相关度R2=0.9872。王婷婷等[5]采用热线法测试几种高性能织物在不同温度环境下的导热性，并利用最小二乘法拟合出相关性曲线。后来随着模拟软件的发展，吴佳佳等[6]采用有限元软件ABAQUS模拟平纹机织物的热传递过程。戈梦夢[7]利用数值模拟计算探讨出平纹机织物的热阻与织物厚度和孔隙率有关。Phillip Gibson[8]建立圆筒状的织物模型，研究环境风速、温度和湿度对传热性质的影响。

关于针织物的热传递性能，赵超等[9]在电脑横机上编织了几种不同结构参数的纬平针织物，探究弯纱深度对织物导热系数的影响。孙玉钗[10]采用热量传递数学模型和有限元计算来分析针织内衣织物热传递性能，将针织絮类夹层衬垫看做是均匀连续体进行研究。但实际上，针织物中纱线相互圈套，含有不规则空气层，所以本文针对针织物结构建立织物几何模型，并导入有限元分析软件中对热传递性能进行计算，通过与实际测试结果对比分析，建立一种评估、优化和预测针织物导热性能的有效方法。

1织物模型建立

1.1织物几何结构

实验样布采用的是纬平针织物，因为纬平针组织为针织的最基本组织，且是日常汗衫的常用组织，对于研究针织物热舒适性能有一定的代表性。样布的材料是棉，因为棉织物轻柔、舒适，且是热量的不良导体，汗衫采用棉材料为了吸湿导汗、柔和贴肤。所以本实验采用三种不同纱线细度、组织密度的棉纬平针织物作为样布，来研究针织物热传递性能，织物规格如表1所示。

1.2构建几何模型

通过YG141D织物厚度测试仪（常州第二纺织机械有限公司）和VHX5000超景深数码显微镜（基恩士公司）对织物尺寸进行测量，并且测量多次求其平均值，得到织物尺寸参数如表2所示。图1为型值点测量位置，其中a、b、c、α、β均为在XY平面内测量，a为点P1到P2的距离，b为P2到P3的距离，c为P4到P5的距离，α为P2P3与P3P4的夹角，β为P1P2与P2P3之间的夹角。

按照测量所得的数据可以确立P1～P4，那么P5～P8关于线段P4P5中心线对称，所以依次确立8个型值点，然后采用非均匀有理B样条曲线构建纱线路径，样条曲线表达式为[11]：

P（u）=∑ni=oWiQiBi，k（u）∑ni=0WiBi，k（u）（1）

式中：Qi表示第i个几何控制顶点;Wi是相对应几何控制顶点的权值，用来调节控制顶点的权重;k为B有理样条曲线的幂次;Bi，k（u）为k次B样条基函数。

本文中k取3，采用积累弦长参数化法[1213]计算样条曲线的矢量节点，对数据点进行严格化规范后可得到一个参数化序列，将其分别对应的矢量点代入到非均匀有理三次B样条曲线函数中，并且使曲线经过几个特殊的插值型值点，以及满足曲线的首尾两端的端点与其型值点重合的条件，联立求解即可得出曲线的控制点。然后经过阵列重复可得到纬平针组织模型，如图2所示。

2织物有限元模拟

2.1模型前处理

模型在导入到有限元分析软件之前需要先切割成需要的结构单元，因为既要代表性地反映整块织物的热传递性能，又要避免模型较大导致计算量大。所以，本实验中将纬平针组织模型切割成单个完整线圈模型，然后将切割好的模型导入到有限元分析软件STARCCM+中，运用布尔运算将固体纱线组合成一个整体，便于网格划分和材质的属性定义，并在固体模型周围建立空气流体区域，然后进行网格划分。网格是模拟计算的基础，网格的大小和质量影响迭代计算速度和最后收敛情况[14]。由于该模型尺寸小、表面屈曲程度较大，所以网格划分时需要特别注意表面连接处的网格质量。利用软件对表面网格质量进行检查，一般情况下，检查面穿透、面质、接近面、自由边、非多重边和非多重面等几项标准，利用自动修复和手动修复相结合，将问题网格一一修复。然后根据面网格可选择划分四面体网格、多面体网格或切割体网格，因为多面体网格有较多的相邻单元，适用于表面屈曲程度大的几何体，并且其梯度计算和流动模拟更为准确，所以本实验中采用多面体网格。

实验中所建立的三个几何模型，在STARCCM+有限元软件中，经过表面修复和自动体网格划分，网格尺寸为0.01mm，最终的网格数量和质量情况分别是：32s棉織物的固体区域147899cells，流体区域286070cells;网格具有拓扑有效性，面有效性为100，体积变化率在0.1～1.00为99.015%。26s棉织物的固体区域175229cells，流体区域312479cells;网格具有拓扑有效性，面有效性为100，体积变化率在0.1～100为99.039%。21s棉织物的固体区域241105cells，流体区域464675cells;网格具有拓扑有效性，面有效性为1.00，体积变化率在0.1～1.00为99.156%。图3（a）为划分网格后的织物纱线模型，图3（b）为划分网格后透明化的整个模型。

2.2边界条件设置

将纱线区域定义为固体域，物理模型采用三维恒密固体域，并设置分离固体焓变等属性条件，固体材料属性依据棉纤维材料进行界定，其中密度850.0kg/m3，导热系数0.072W/（m·K），比热值1275J/（kg·K）。将外围空间定义为流体域，物理模型采用三维层流气体域，并设置恒密度、分离流、分离流体焓变等属性条件。空气流体的属性可设置为默认数值，密度1.184kg/m3，导热系数0026W/（m·K），比热值1003.62J/（kg·K）。边界条件的设置如图4所示，将流体域上表面top和下表面bottom的边界设置为压力出口pressure outlet，而四周的面设置为壁面，图4模型边界

Fig.4Model boundary不进行质量和热量交换。其中上表面的初始温度设置为20℃，下表面的初始温度设置为35℃，这是因为在实验条件下，下表面所接触的热板为35℃，气候室的温度为20℃。

因为模型上下表面存在温度差，所以流体中的分子运动和固体中的声子运动可实现能量和质量的传递[15]，传递过程中遵循控制方程如下[16]：

质量守恒方程：

ρt+xi（ρui）=0（2）

动量守恒方程：

tρui+xjρuiuj=-pxi+τijxj+ρgi+Fi（3）

能量守恒方程：

tρh+xiρuih=xik+kiTxi+Sh（4）

式中：ρ为流体密度，t为时间，p为静压力，h为熵，k为分子传导率，ki为由湍流传递而引起的传导率，ui为流体速度沿i方向的分量，uj为流体速度沿j方向的分量，xi为i方向的坐标，xj为j方向的坐标，τij为应力矢量，gi为i方向的重力分量，T为温度，Sh为定义的体积源。

2.3后处理及分析

将各区域模型的属性和条件设置完成后，创建衍生截面用于模拟计算后的分析，并建立所需要的数据报告，以便于计算织物系统的热阻、克罗值等相关数据。先进行初始化运行，然后运行迭代计算，图5为步长为0.01s，迭代计算5000步后的温度云图。从监控的残差曲线图上可看出，此时质量和能量的传递已经趋于稳定，所以截取此时的温度云图用于可视化分析。图5（a）（b）为织物上表面和下表面的云图，可以看到温度在纱线表面的分布情况，离接触面越近的部位温度越接近外表面边界的温度。图5（c）为平行于模型XY平面，并且在Z方向上模型系统的1/2位置处的截面云图，可以看到“月牙”形的温度差异，所以在纱线交织部位，沿纱线传递的热量比空气传递热量快。图5（d）为平行于模型YZ平面，并且在X方向上模型系统的1/4位置处的截面云图，可以看到沿纱线轮廓有“波浪”形的温度变化，所以在沿Z方向传递的过程中，热量在固体纱线与空气流体交界面传递时出现滞后现象，这是因为二者的物理属性不同。

3实验与模拟结果对比

3.1热舒适性实验

测试织物导热性能，采用国家标准GB/T11048—2018《纺织品生理舒适性稳态条件下热阻和湿阻的测定（蒸发热板法）》，图5温度云图

Fig.5Temperature cloud使用YG606G热阻湿阻测试仪（宁波纺织机械有限公司）进行测试，测试仪器实物如图6所示，原理如图7所示。按照标准设置相关参数，先测试该仪器的空板热阻Rct0，再将60cm×60cm的织物样布放入测试板上进行测试，利用下式自动计算出织物的热阻值Rct。

0=（Tm-Ta）·AΔH-Hc（5）

Rct=（Tm-Ta）·AH-ΔHc-Rct0（6）

式中：Rct0为仪器空板热阻，m2·K/W;Rct为织物样品的热阻，m2·K/W;Tm为实验板的温度，℃;Ta为气候室的温度，℃;A为实验板的面积，m2;H为提供给加热面板的测试功率，W;ΔHc为热阻测定中的加热功率的修正量。

3.2织物系统热阻计算

棉纤维纱线的导热系数是已知的，但是棉纱线以不同的形态结构织成织物后，织物系统的整体热阻不是空气和纱线热阻的简单叠加，并且空气和纱线的形态均不规则。所以在计算织物系统热阻时，采用的是傅里叶定律求得热流密度，再类比电阻电流的关系推导出热阻值[17]。

q=-λTx=φA0（7）

式中：q为热流密度，W/m2;λ是导热系数，W/m·℃;Tx是沿热量传递方向的温度梯度;φ为转移总热量，W;A0为单元模型垂直于Z方向的截面面积，m2。

织物系统的热阻由式（7）推导而出：

R=Tb-Ttq（8）

式中：Tb为织物系统下表面平均温度，℃;Tt为织物系统上表面平均温度，℃。

3.3实验值与模拟值对比

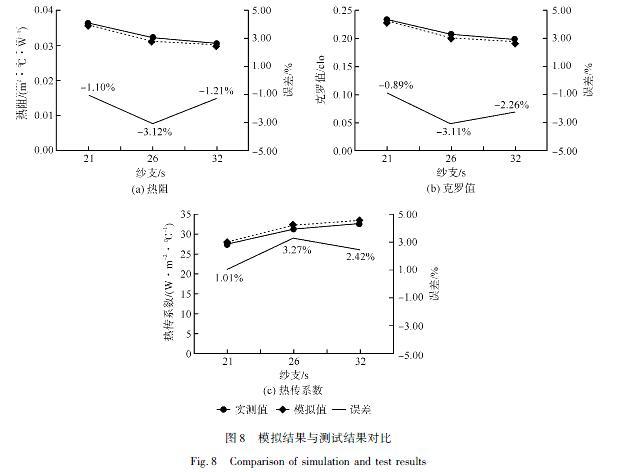
根据式（7）和式（8）可计算出单元织物系统的热阻，然后织物的克罗值约为热阻值的6.45倍，传热系数为热阻值的倒数，由此可以计算得到克罗值与热传系数。有限元模拟计算的结果与实际测量结果的对比如图8所示。从图8可看出，三种不同规格的棉针织物导热性能不同，纱线较粗的织物热阻较大，但是三种均是常用汗衫面料，总体热阻较小，方便夏季人体热量散失、保持凉爽。通过模拟计算所得热阻、克罗值、热传系数与实际测量值的误差在4%以内，其中21s棉纱针织物的模拟结果误差仅在1%左右。模拟计算出的热阻值略小于实际测量值，分析认为是因为在进行建模时，没有将纱线表面的毛羽考虑在内，而在实际测量中，表面毛羽对热阻的测量有一定的影响。但其误差在可接受范围内，表明该方法具有一定的實用性。

4结论

为了建立织物几何模型，采用超景深数码显微镜和织物厚度仪测量织物结构尺寸，利用参数数据，插入非均匀有理B样条曲线来构建纱线弯曲路径，通过扫描、阵列及切割得到单元线圈模型。将线圈模型导入到有限元分析软件中分析热传递性能，通过温度云图可清晰看到热量在织物表面的分布情况，以及分析内部截面的温度分布，热量沿固体纱线传递比空气要快，但在二者交界面上出现滞后现象。最终三种不同规格的纬平针织物模拟计算结果，其热阻值、克罗值和热传系数与实际测量值的误差在4%以内，说明通过建立针织物几何模型对织物热传递进行有限元仿真可以反映、预测织物的导热性能，为优化设计织物提供理论依据，为进一步研究针织物其他仿真，如导湿、电磁辐射等打下基础。

参考文献：

[1]杨勇， 范君. 浅谈服装的热湿舒适性[J]. 黑龙江纺织， 2010（3）： 1416.

YANG Yong， FAN Jun. Discussion on the heatwet comfortability of clothing[J]. Heilongjiang Textile， 2010（3）： 1416.

[2]宋兰霞， 陈昀. 织物结构密度对织物导热性能影响的研究[J]. 中国纤检， 2005（3）： 2225.

SONG Lanxia， CHEN Yun. Study on the influence of fabric density on thermal conductivity of fabrics [J]. China Fiber Inspection， 2005（3）： 2225.

[3]吴海军， 钱坤， 曹海建. 织物结构参数对热传递性能的影响[J]. 纺织学报， 2007（2）： 2123.

WU Haijun， QIAN Kun， CAO Haijian. Effect of fabric structure parameters on its heat transfer property[J]. Journal of Textile Research， 2007（2）： 2123.

[4]刘让同， 刘淑萍， 李亮， 等. 织物结构对机织物热传导的影响[J]. 上海纺织科技， 2017， 45（6）： 47.

LIU Rangtong， LIU Shuping， LI Liang， et al. Effect of fabric structure on heat conduction of woven fabrics[J]. Shanghai Textile Science & Technology， 2017， 45（6）： 47.

[5]王婷婷， 刘晓霞， 庄明宇. 不同温度环境下织物导热机理的探讨[J]. 上海纺织科技， 2015， 43（11）： 2226.

WANG Tingting， LIU Xiaoxia， ZHUANG Mingyu. Discussion on the thermal transfer mechanism of fabrics at different temperatures [J]. Shanghai Textile Science & Technology， 2015， 43（11）： 2226.

[6]吴佳佳， 唐虹. 应用ABAQUS的织物热传递有限元分析[J]. 纺织学报， 2016， 37（9）： 3741.

WU Jiajia， TANG Hong. ABAQUS based finite element analysis of heat transfer through woven fabrics [J] Journal of Textile Research， 2016， 37（9）： 3741.

[7]弋夢梦. 机织物热传导性能及其数值模拟[D]. 郑州： 中原工学院， 2018.

YI Mengmeng. Thermal Conductivity of Woven Fabric and Its Numerical Simulation [D]. Zhengzhou： Zhongyuan Institute of Technology， 2018.

[8]GIBSON P. Modeling heat and mass transfer from fabriccovered cylinders [J]. Journal of Engineered Fabrics & Fibers， 2009， 4（1）： 18.

[9]赵超， 杨彩云. 弯纱深度与针织物结构参数及导热系数间的关系[J]. 国际纺织导报， 2015， 43（11）： 2224.

ZHAO Chao， YANG Caiyun. Relationship among the sinking depth and structure parameters and thermal conductive performance of knitted fabric[J]. Melliand China， 2015， 43（11）： 2224.

[10]孙玉钗. 针织物热舒适性能研究与针织保暖产品设计[D]. 上海： 东华大学， 2005.

SUN Yuchai. Study on Thermal Comfort Properties of Knitted Fabrics and Design of Heat Preservation Products for Knitting [D]. Shanghai： Donghua University， 2005.

[11]RAJAB K， PIEGL L A， SMARODZINAVA V. CAD model repair using knowledgeguided NURBS [J]. Engineering with Computers， 2013， 29（4）： 477486.

[12]施法中. 计算机辅助几何设计与非均匀有理 B 样条[M]. 北京： 高等教育出版社， 2001： 47.

SHI Fazhong. ComputerAided Geometry Design and NonUniform Rational BSpline [M]. Beijing： Higher Education Press， 2001： 47.

[13]汝欣， 彭来湖， 吕明来， 等. 纬编针织物几何建模及其算法[J]. 纺织学报， 2018， 39（9）： 4449.

RU Xin， PENG Laihu， L Minglai， et al. Modelling and algorithm of weft knitted fabric[J]. Journal of Textile Research， 2018， 39（9）： 4449.

[14]代文杰， 邱华， 杨恩惠， 等. 基于ANSYS CFX的织物透气性数值计算[J]. 丝绸， 2018， 55（9）： 5156.

DAI Wenjie， QIU Hua， YANG Enhui， et al. Numerical calculation of fabric air permeability based on ANSYS CFX[J]. Journal of Silk， 2018， 55（9）： 5156.

[15]胡海霞， 孟家光. 织物热传导机理的分析和探讨[J]. 北京纺织， 2005（6）： 2831.

HU Haixia， MENG Jiaguang. The analysis and discussion of heat transmission mechanism of the fabrics[J]. Beijing Textile Journal， 2005（6）： 2831.

[16]李明， 刘楠. STARCCM+11.0与流场计算[M]. 北京： 机械工业出版社， 2017： 78.

LI Ming， LIU Nan. STARCCM+ 11.0 and Flow Field Calculation [M]. Beijing： Mechanical Industry Press， 2017： 78.

[17]李瑛慧， 谢春萍， 刘新金， 等. 仿真丝织物与真丝织物的热传递有限元仿真[J]. 丝绸， 2017， 54（12）： 711.

LI Yinghui， XIE Chunping， LIU Xinjin， et al. Finite element simulation of heat transfer on silklike fabrics and real silk fabrics [J].Journal of Silk， 2017， 54（12）： 711.

收稿日期： 20190403; 修回日期： 20191129

基金项目： 江苏省产学研项目（BY201602214）

作者简介： 杨恩惠（1994），女，硕士研究生，研究方向为针织物热湿舒适性的仿真研究。通信作者：邱华，教授，qiuhua@jiangnan.edu.cn。