模糊时间下考虑碳税值变化的多式联运路径优化问题研究

蒋琦玮 林 艺 冯芬玲

1（中南大学交通运输工程学院， 长沙 410075） 2（中南大学土木工程学院， 长沙 410075）

引言

随着现代物流企业对低成本和高时效的运输方式的追求，集装箱多式联运受到越来越多的关注，加快多式联运提速发展是大势所趋。国务院办公厅印发的《推进运输结构调整三年行动计划（2018～2020 年）》 作出明确指示，要求打赢蓝天保卫战、打好污染防治攻坚战，提高综合运输效率、降低物流成本［1］。多式联运拥有单一运输方式无法比拟的优势，如何选择运输线路和运输方式显得尤为重要，探究建立政策引导机制来推动交通供给侧结构性改革是本文的现实意义所在。

国内外学者对多式联运的研究成果丰硕，学者们常把运输经营者看重的成本最低和客户最感兴趣的货物的及时性或线路的可靠性等纳入考虑因素［2，3］。但在以往的研究中，很多与运输活动相关的参数，如货物的品种、需求量、运输时间等经常被默认为确定值，这与实际不太符合。近年来，学者们的研究更贴近运输实际情况，并对这些不确定参数展开研究。张得志和李双艳［4］考虑到多式联运中运输和转运时间的不确定性、转运的可能性以及时间窗限制等情况，构建具有时效性的多式联运协同优化模型。Fazayeli 等［5］在研究多式联运路径选择时，为更大限度地提高客户满意度引入了时间窗约束，需求假设为模糊数，建立了一个混合整数模糊数学模型。Wang 等［6］研究不确定条件下，基于中心辐射网络的公铁多式联运系统的建模与优化问题，以成本和时间为目标函数并用加权和法处理多目标问题。

随着节能减排理念深入人心，运输中的碳排放问题不容小觑。越来越多的学者开始关注碳排放量对货物运输路径决策的影响［7，8］。冯芬玲和张清雅［9］考虑了环境对多式联运运输方式选择的影响，给出了运输耗费、安全事故、能源消耗和环境污染这4 个因素的计算方法并将其纳入到社会总成本中，符合社会倡导绿色发展的主题。滕岚［10］研究确定性环境下多式联运路径优化，对比了不考虑碳成本和考虑碳成本两种情况下的最优方案，采用例举法求解模型，但没有探讨碳税值逐步增加时多式联运路径方案的改变。Liao 等［11］采用基于活动的排放模型对运输中产生的二氧化碳进行测算，研究发现采用多式联运方式替代长途卡车运输，可以显著降低二氧化碳排放量。Zhang等［12］采用双层规划模型分析碳定价策略、多式联运网络终端布局优化和服务网络优化设计多种策略组合对发展多式联运的促进作用。研究发现与单一策略类型所产生的最佳性能相比，组合多种策略类型具有更好的网络性能。成耀荣和谭维［13］研究货物从同一起点运往不同终点的多任务多式联运路径优化问题，并对多个运输任务进行整合，考察碳排放对运输方案的影响，文章局限于对运输时间确定情况下的多式联运路径研究。Lam 和Gu［14］建立以成本、时间和碳排放量最小为目标的多式联运网络优化模型，设计遗传算法求解，并以我国的一个内陆城市进出口集装箱为例进行分析，提出了协调过渡时间和不同碳排放限制对多式联运网络设计的影响。

已有的多式联运路径优化的研究，多集中在确定性环境下的路径优化，实际上运输过程不可避免地受到交通堵塞、天气条件等不确定性因素的影响，为贴近实际的运输情况，本文将运输时间、转运时间设为随机数；另外现有文献虽在多式联运路径优化问题建模时考虑了碳排放成本限制，但较少有学者研究碳税值逐级增加时多式联运路径变化，并探讨相应地总成本及碳排放量的变化。

1 问题描述

某一批货物从城市O 运往城市D，运输过程途径若干中间节点，任意两节点间有多种运输方式可供选择，不同运输方式的运输距离及所对应的运输费用不同，选用不同运输方式的二氧化碳排放量也不同，运输时间、转运时间设为随机数。本文求解包含碳排放成本在内的总成本最小问题，对多式联运过程的运输路径和运输方式作出决策，要求承运人将货物送达终点时满足一定置信水平的时间窗限制。本文假定：

a.假设相邻两个节点之间货物运输不可分割，即在两节点间只能选择一种运输方式；

b.货物在任意节点中转次数不超过1 次；

c.在运输过程中不发生货物的增加或减少，也没有转运节点的补货或者减货；

d.假设货物在转运节点不进行仓储，转运完成即运往下一个目的地，不考虑仓储费用；

e.假设运输线路的容量足够大，每个节点没有转运能力限制；

f.假设根据调查，各城市节点间的运输时间、不同运输方式的转运时间均服从正态分布。

2 模型构建

2.1 符号定义

多式联运网络为G（N，A，M），符号定义见表1。

表1 参数、常量、变量的说明

续 表

2.2 目标函数及约束条件

根据问题假设和符号定义构建考虑碳排放成本的不确定环境下多式联运路径决策模型：

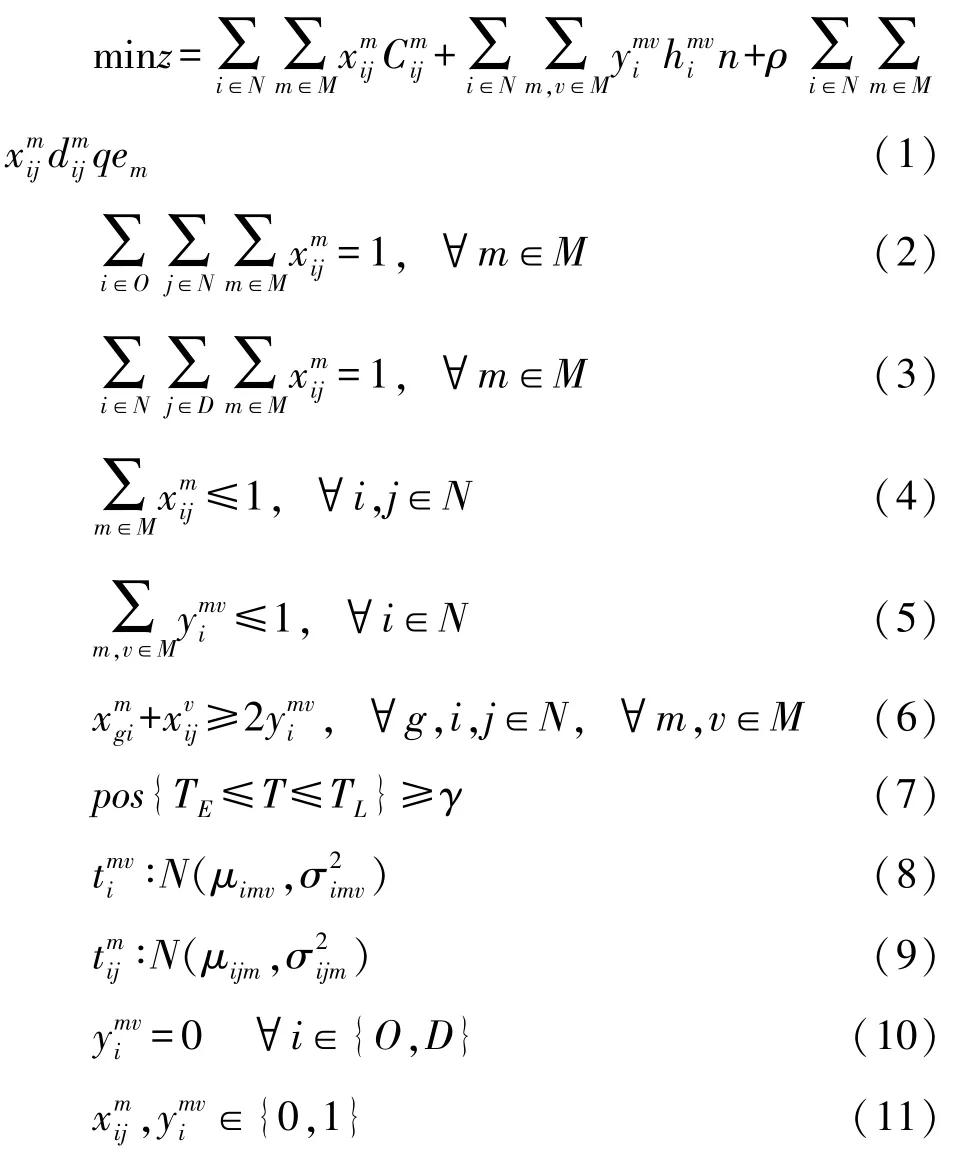
式（1）为目标函数，即运输费用、转运费用和碳排放费用最小。碳排放主要产生于运输过程中，本文只考虑运输过程中产生的碳排放量，用碳排量乘一定的碳税值ρ可得碳排放费用。式（2）和式（3）分别表示货物只能从一个起点出发、到达某一终点；式（4）表示货物从节点i运送至j时不可拆分，最多只能选择一种运输工具；式（5）表示在每个节点最多只允许1 次转运；式（6）保证运输的连续性，即如果在节点i货物的运输方式由m转为v，则必是用运输方式m到达i，再用运输方式v从i点离开；式（7）表示货物送达终点时，时间窗的随机机会约束，γ为置信水平；式（8）和式（9）表示转运时间、运输时间都服从正态分布；式（10）表示起点和终点货物不发生转运；式（11）表示决策变量取整数0 或1。

3 算法设计

3.1 模糊模型清晰化处理

将模糊机会约束规划模型转化为一个确定性的模型后求解，参考李雅普诺夫中心极限定理对约束式（7）进行转化。都是相互独立且服从正态分布的随机数，则有：

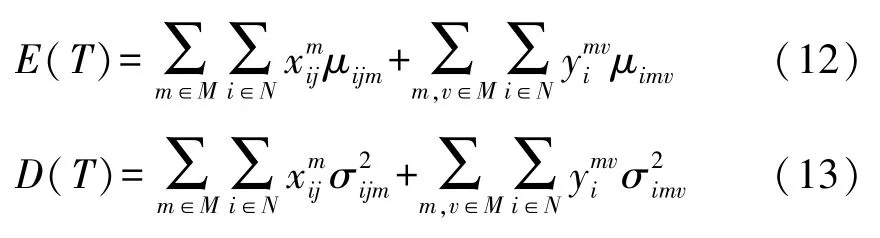
由李雅普诺夫中心极限定理可知，多个（≥10）相互独立随机变量的和近似服从正态分布。该定理可表示为近似服从正态分布，即pos｛η≤A｝＝ϕ（A），ϕ为标准正态分布函数；式（7）的等价形式为：进一步可表示为：

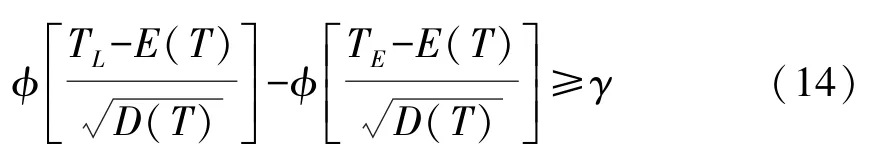
孙彬［15］的研究已证明正态分布下的式（14）与机会约束式（7）是完全等价的。

3.2 遗传算法的步骤

设运输网络共有N个城市节点，导入基础数据，且根据距离矩阵得出运输方式转运的备选集矩阵B，运输方式转运的备选集矩阵和距离矩阵都是三维矩阵，的值为正实数时表示中转是符合实际的，此时备选集矩阵中对应位置上的值置为1，若距离值为无穷大则表示节点i到节点j不能通过运输方式m实现，相应的值为0。

Step1：染色体编码

需对货物从起点到终点的路径和运输方式进行规划，涉及的决策变量有。种群中的每个个体长度为（2N-1），由两小段组成，前一段（前N个数）是运输路径编码，规定起点编号放在第一位，其余的节点编号随机排列。后一段（N＋1～2N-1）是运输方式的编码，要求在满足运输方式转运的备选集的前提下从1～3 之间的整数中随机生成。

多式联运方案不需要遍历所有城市节点，在计算时只截取起点到终点编号之间的片段。

Step2：初始化种群

在初始化种群时除了筛选一些满足置信水平的个体进入种群，还加入一些随机产生的个体以保证种群多样性。并对染色体进行去重复化处理，确保初始种群中没有完全相同的个体。

Step3：适应度函数

设f（a）表示第a个个体所对应的运输加转运成本，t（a）表示第a个个体的运输时间。机会约束与所规定的置信水平的差异度用N（a）表示（其中β≺1）：

式中fmin、fmax分别为f（a）的最小值和最大值。

Step4：选择算子

根据轮盘赌规则选出一定数量的个体。

Step5：交叉算子

采用单点交叉的方式，选择每一个体的三号位点进行交叉。

如父染色体：

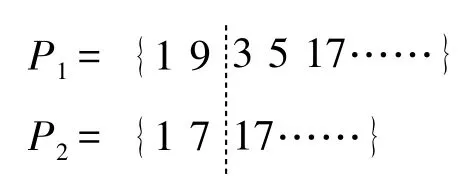
交叉后的子染色体：

路径不能出现折返，在交叉操作完成后需进行检查是否有重复的节点出现。

Step6：变异算子

依据变异概率，随机选择个体进行变异，途径节点和运输方式两段均可参与变异，对运输路径的编码进行变异操作时，将变异位点取在起点编号到终点编号之间的某个位置；对运输方式的编码进行变异操作时，数值范围限定为1～3 之间的整数。

Step7：重插入算子

经过交叉变异后可能出现不满足要求的个体，用淘汰算子找出不满足节点运输方式备选集或者不满足时间窗置信水平要求的非可行解，将选择操作前的种群选择部分用来补充，使规模与之前一致。

当满足设置的终止条件时，算法终止并输出全局历史最优解，否则继续迭代。

4 算例分析

本文选取17 个城市节点构成的运输网络，节点编号1～17 依次为南宁、重庆、南昌、宁波、合肥、武汉、长沙、南京、上海、杭州、福州、郑州、广州、西安、贵阳、青岛、成都，每相邻两个城市之间最多有公路、铁路、水路3 种运输方式，假设有8 个运输任务，每个运输任务都是运送800t 重的货物，货物采用20ft 集装箱装运，40TEU 正好装载完成。设定每个运输任务的γ＝0.8，β＝0.3。

各城市间不同运输方式的运输距离数据通过火车票网及相关文献得到（表略）。若节点i到节点j之间不能通过运输方式m到达，则将其对应位置上的数字设置为无穷大。

考虑到两节点间不同运输方式的运输时间均值数据难以获取，本文假定运输距离与运输速度之比即为运输时间的均值，其中公路运输速度取100km／h、铁路70km／h、水路34km／h。公路运输的方差都取0.52，铁路运输的方差取0.22，水路运输的方差取0.752。公路和铁路集装箱运输费用由式（17）求得，水路集装箱运输费用由式（18）求得。运输费用公式中的参数取值参考梁晓慷［16］的研究，以20ft 集装箱为例，具体数值如表3。各运输方式下碳排放因子分别为公路运输：0.04795kg／t·km，铁路运输：0.00841kg／t·km，水路运输0.01733kg／t·km［17］。其他参数如表4～5所示。

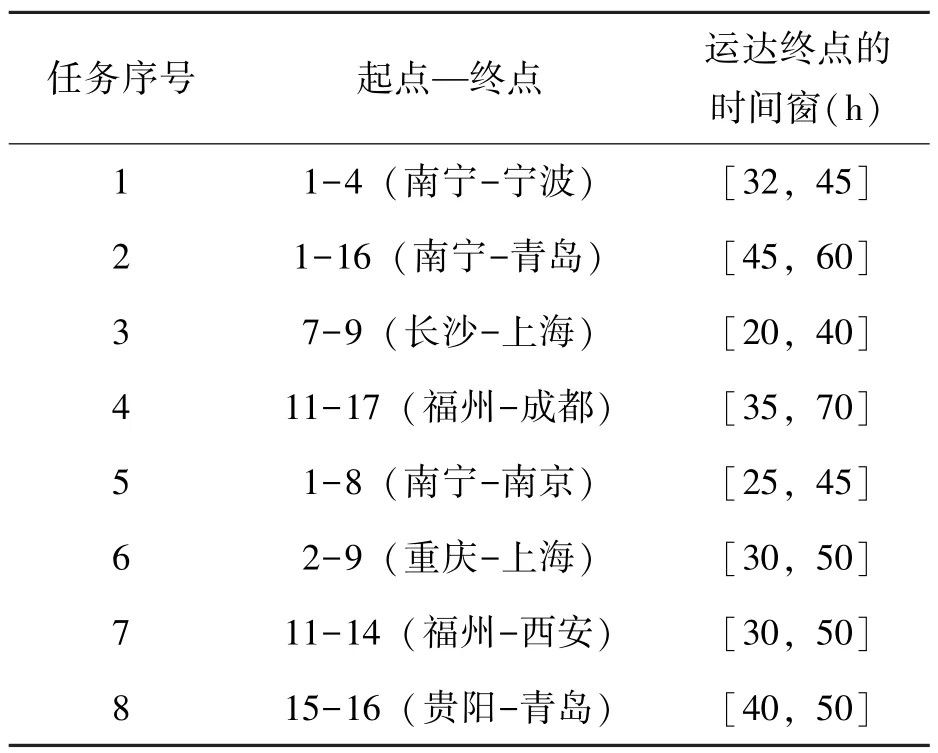
表2 运输任务表

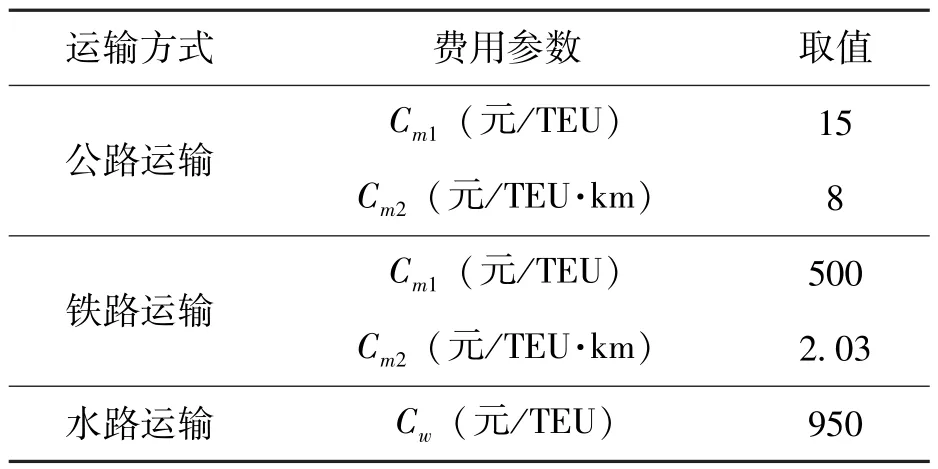
表3 运输费用参数取值

表4 不同运输方式之间的转运时间（h）

式（17）中m＝1 或2，Cm1表示与货运量有关的单位运输费用参数（单位：元／TEU），Cm2表示与中转量有关的运输费用参数（单位：元／TEU·km），n 为集装箱个数（单位：TEU）。式（18）中m＝3，Cw为与货运量相关的单位运输费用参数（单位：元／TEU）。水路运输参考我国集装箱班轮费用核算标准，采用包干计费为Cw＝950 元／TEU。

表5 各运输方式的转运费用（¥ ／TEU）

算法参数设置如下：选择概率为0.8，交叉概率为0.8，变异率为0.01，种群规模为60，最大迭代次数为100，算法采用Matlab R2016a 实现。

根据我国目前的形势，普遍倡导按照每吨二氧化碳征收人民币10 元，但这比全世界的平均水平还要低。据世界银行2017 年11 月发布的碳定价的现状和趋势报告［18］可知，各国的碳定价差异很大，每吨二氧化碳定价在1～140 美元之间，其中瑞典的碳税税率最高，达到140 美元／tCO2e（约合人民币997 元）。有研究证明［12］碳定价水平超过600 欧元／tCO2时，铁路运输才会有明显优势，据此，我国目前的碳定价水平对推动交通供给侧结构性改革的作用微乎其微，考虑到未来随着碳定价机制的成熟，我国的碳定价会逐步提高，本文探究碳税值的变化对总成本和碳排放量的影响时，以0.1 元／千克二氧化碳逐级递增进行测算。

由表6 可知，在总成本最小的目标下，任务1～4 在不考虑碳排放成本时有公路参与运输过程，随着碳税值的增加，运输方案迅速调整，在碳税值为0.1～0.3 元／千克二氧化碳时转为铁水联运或者铁路运输。任务5～8 在不考虑碳排放成本时已经是铁水联运完成整个运输过程，后续随碳税值的增加，运输方案的变化不太敏感，任务7 随着碳税值的增加未发生运输方案的变化。

探讨碳税值对碳排放量的影响，碳税值的增加能促成“公转铁”，任务1～4 改变运输方案后碳排放量减少明显；任务5～8 在不考虑碳排放成本时已经是铁水联运，碳排放量相对小，提高碳税值后尽管可能带来运输方案的调整，但碳减排效果不如任务1～4。

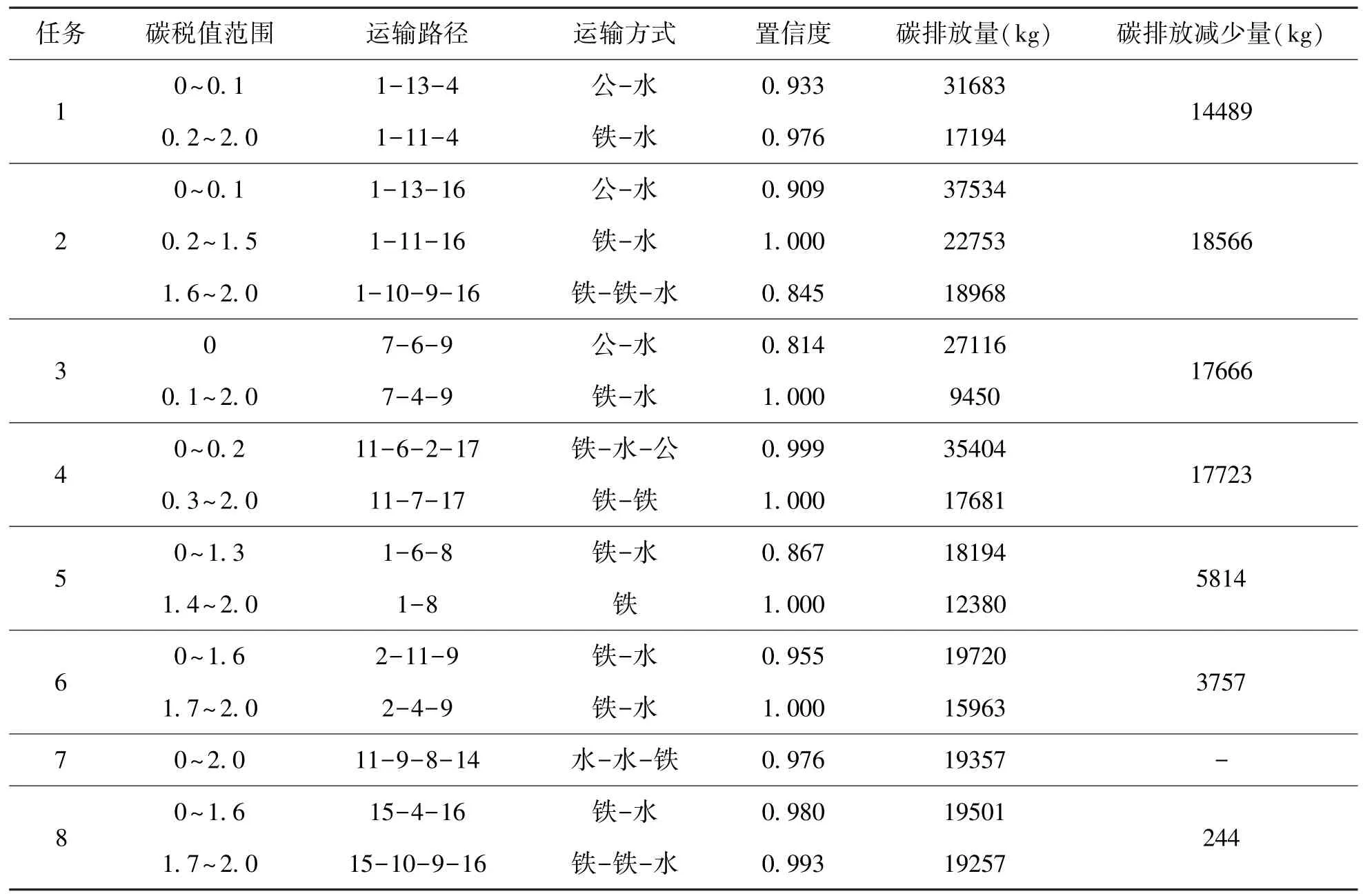
表6 各运输任务在不同碳税税率下的路径变化

各运输任务的总成本随碳税值变化的情况如表7 所示。随着碳税值的增加，每个运输任务总费用不断上升，为探究运输方案调整后总成本增长幅度的变化，取任务3、5、7 的3 组数据绘制图1，任务7 没有运输方案的调整，因此总成本增长幅度是均匀的，任务3 和任务7 随着碳税值的增加都有一次方案的调整，容易看出调整运输方案后，总成本的增长幅度较没调整之前变小。

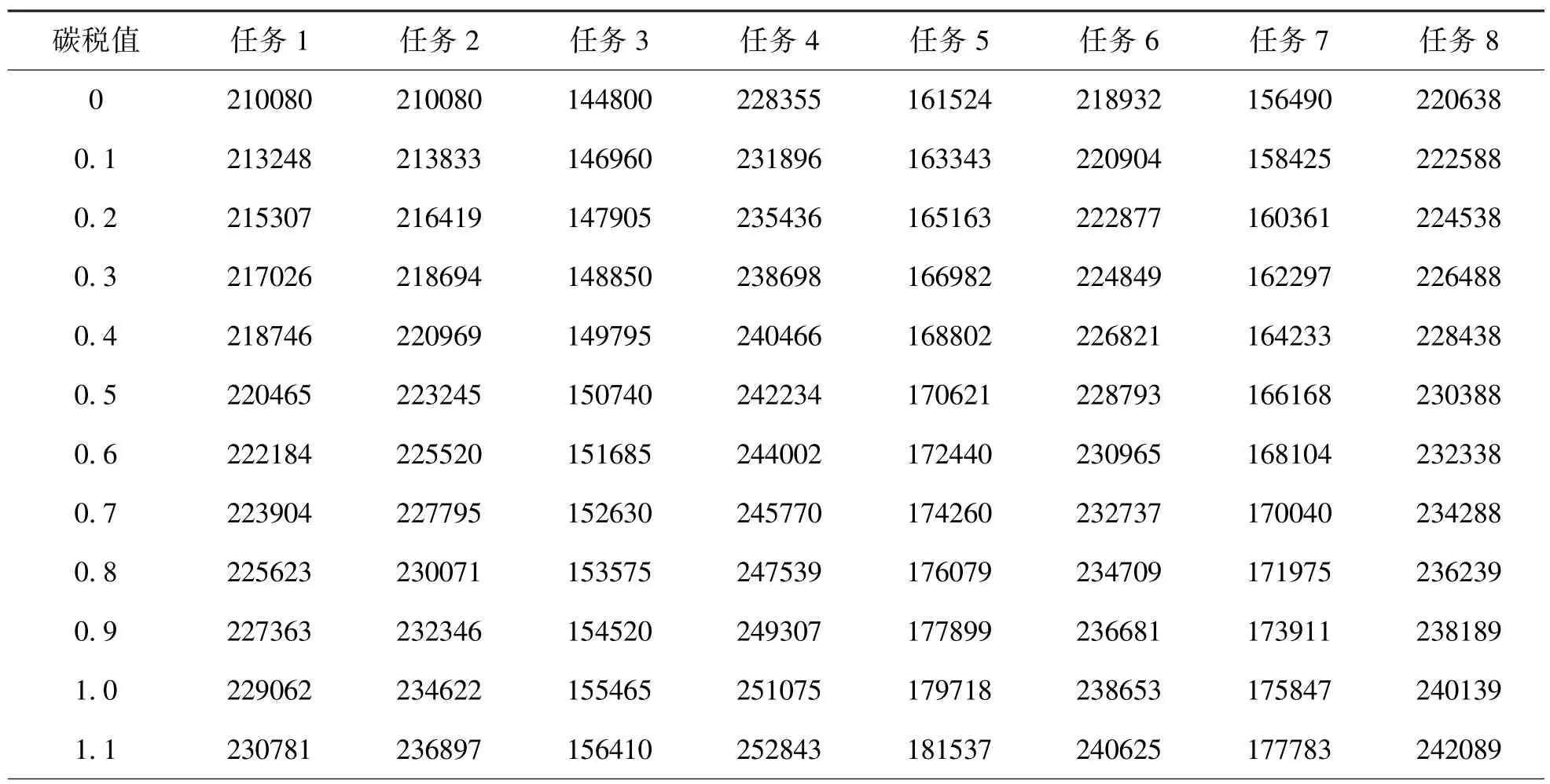
表7 各运输任务的总成本随碳税值变化时的情况

续 表

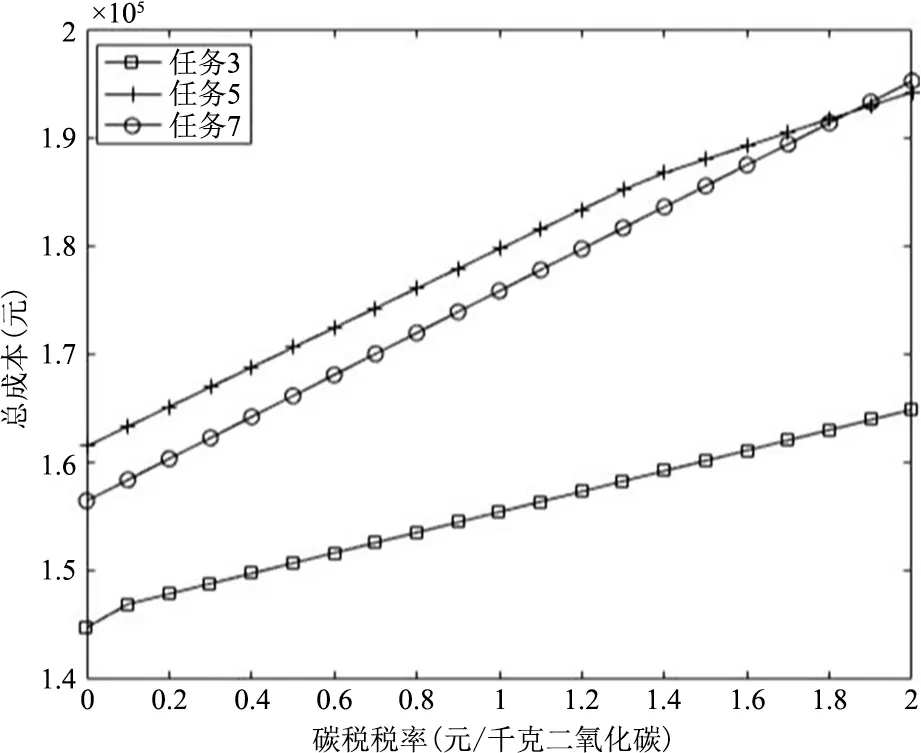
图1 不同碳税税率下的总成本变化

5 结论

本文探究了运输时间不确定的集装箱多式联运路径优化问题，把碳排放成本内部化为总成本，构建机会约束模型并采用遗传算法求解，通过构建含17 个城市节点的运输网络，求解8 对任意起终点的运输任务在碳税值逐级递增时的运输方案规划，并探究由此总成本和碳排放量的变化规律，结论如下：

（1）本文的模型与算法适用于一个运输网络中，给定各节点之间不同种运输方式的运输距离后，对任意的起终点对进行运输方案的规划，本文构建的模型在为多式联运承运人提供方案决策时能有效引导其选择经济且环保的运输方案。

（2）算例结果表明，公路运输对总成本和碳排放量方面都存在不利影响，且有公路运输参与的多式联运过程对碳税值的增大较为敏感，在税率为0.1～0.3 元／千克氧化碳时转为铁水联运或者铁路运输，由此带来的碳减排效果也十分明显。这说明货物在满足运达终点的时间窗限制的前提下，碳税值增加能有效促进“公转铁”，相关部门在征收碳税时要对碳税值进行灵敏度分析，综合考虑选择使碳排放量发生变化的临界值点。

（3）对于不考虑碳排放成本时运输方案已经是铁水联运的多式联运过程，此时碳排量相对较小，后续随碳税值的增加运输方案的变化不敏感，即持续增加碳税税率最优方案可能不会再变化，碳减排效果不太明显。因此碳税值不宜定的过高，否则只会徒增货运企业的负担。对多式联运承运人或货运企业的启示是：在我国倡导低碳运输、降低物流成本的大背景下，应充分利用铁路与水路的优势，响应国家政策号召。