A new diagnosis strategy under the PMC model and applications①

Liang Jiarong (梁家荣),Chen Fang,Zhang Qian

(*School of Computer and Electronic Information,Guangxi University,Nanning 530004,P.R.China)(**Guangxi Key Laboratory of Multimedia Communications and Network Technology,Nanning 530004,P.R.China)

Abstract

Key words:Double-Syndrome diagnostic,(k,t)-diagnosable,(k,t/t)-diagnosable,hypercube,2D(3D) mesh,permutation star graph

0 Introduction

With the rapid development of multiprocessors,multiprocessor computer systems contain hundreds and thousands of processors now[1].It is inevitable that some processors in such a system may fail.To ensure reliability,the system should have the ability to identify the faulty processors which are then isolated from the system or replaced by additional fault-free ones[2].In order to maintain the reliability of the system,automatic diagnosis procedures were proposed by Preparata et al.[3]and Somani et al.[4],which is known as system-level diagnosis.Preparata et al.[3]proposed the first system-level diagnosis model,namely the PMC model,which can be represented by a digraphG=(V,E) and the edge (i,j) means nodeitests nodej.A test resultω(i,j) is associated with each (i,j) andω(i,j)=1(0) ifievaluatesjto be faulty (fault-free).A complete set of test results associated with the edges of the system is called a syndrome[5-7].For a syndromeσ,letω(σ:i,j)=ω(i,j) whereω(i,j)∈σ.Under the PMC model,there are 2 fundamentally different strategies to system-level diagnosis:t-diagnosis[3]andt/t-diagnosis[3-9].A system ist-diagnosable if and only if all the nodes can be identified by the system correctly in the presence of mosttfaulty nodes[10].And a system ist/t-diagnosable if and only if all the faulty nodes can be isolated by it to within a set of size at mosttin the presence of at mosttfaulty nodes[11,12].However,the diagnosability (t-diagnosable andt/t-diagnosable) of a system given byG=(V,E) is nearly depending on the degree of the graphG,which results in that the improvement of the diagnosability of one system by using traditional method becomes increasingly difficult[11-16].Therefore,this provides a strong motivation to discover a new diagnosis method,for which more faulty nodes can be identified correctly.Next section will present a new diagnosis method,called Double-Syndrome diagnostic,under the PMC model,for which more faulty nodes can be identified correctly.Section 2 proposes a new system called (k,t)-diagnosable and the characterization and some properties of such systems are also presented.Section 3 proposes a new system called (k,t/t)-diagnosable system and the characterization and some properties of such a system are also presented.Section 4 uses properties of these 2 systems and Double-Syndrome diagnostic to further increase the number of faulty nodes which can be identified correctly.In Section 5,a further study is proposed on above 2 diagnosable systems under the conditional diagnosis and figure out some special conditional diagnosability of above 2 diagnosable systems.In the last section,a conclusion is drawn.

1 Double-Syndrome diagnostic

Under PMC model,for a system given byG=(V,E),letΓu={v|(u,v)∈E,u,v∈V} andΓu-1={v|(v,u)∈E,u,v∈V}.Similarly,for any subsetX⊂V,ΓX=∪u∈XΓu-XandΓX-1=∪u∈XΓu-1-X.Without loss of generality,letΓu={v0,v1,v2,v3,…,vm} and for a syndromeσi,letω(u,σi)=(ω(σi:u,v0),ω(σi:u,v1),ω(σi:u,v2),…,ω(σi:u,vm)).

Lemma1For a system given byG=(V,E) and 2 different syndromesσ1andσ2,u∈V,ifω(u,σ1),ω(u,σ2),thenuis a faulty node.

ProofSuppose that,to the contrary,uis fault-free.Sinceω(u,σ1),ω(u,σ1),there exists someω(σ1:u,vk) such thatω(σ1:u,vk)，ω(σ2:u,vk).Without loss of generality,letω(σ1:u,v0)=1 andω(σ2:u,v0)=0.ω(σ1:u,v0)=1 impliesv0is faulty.On the other hand,ω(σ2:u,v0)=0 impliesv0is fault-free,a contradiction complete the proof.

Now,Double-Syndrome diagnostic (Algorithm 1) is introduced as follows.

Algorithm1Double-SyndromediagnosticRequire: AsystemgivenbyG=(V,E)withnnodesand2dif-ferentsyndromesσ1andσ2.Ensure: Asetoffaultynodes. 1)Foreachnodevi∈V(0≤i≤n-1),ifω(vi,σ1)=ω(vi,σ2),continuetheDouble-Syndromediagnostic,otherwise,markviwithfaultandcontinuetheDouble-Syn-dromediagnostic. 2)Outputthenodesmarkedwithfault.

Under the PMC model,the test result of one faulty node testing the other nodes is unreliable[15,16].In other words,the value ofω(u,v) is stochastic whereuis a faulty node.For convenience,the possibility of test result 1(or 0) of each faulty node testing other nodes is equivalent and letP(u,v:1)=α(P(u,v:0)=1-α) be the possibility of test result 1(0) of one faulty nodeutesting another nodev(vcan be faulty or fault-free).

Definition1LetAbe a event andP(A)be the possibility of the eventAhappened.

Property1For a system given byG=(V,E),suppose thatu∈Vis a faulty node with |Γu|=m.For any 2 stochastic syndromesσ1andσ2,letP(u) be the possibility thatuis not marked with fault by Double-Syndrome diagnostic.ThenP(u)=P(ω(u,σ1)=ω(u,σ2))=αl×(1-α)kwithl+k=m.Without loss of generality,letα≥0.5,thenP(u)≤αm.

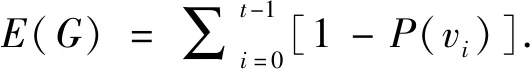
Definition2A regular graph is a graph,in which each vertex has the same number of neighbors.LetD(G) be the number of neighbors of each vertex inG=(V,E).

Property3For a system given byG=(V,E) withnnodes andtfaulty nodes.IfG=(V,E) is a regular graph,thenE(G)=t(1-p(v)),wherev∈Vis a faulty node.

The lower bounds ofE(G) under then-dimensional hypercube with a differentαare shown in Table 1.Here,tdenotes the exact faulty number in the system.

Table 1 The changes of E(G) of n-dimensional hypercube

For a system given byG=(V,E),averageE(G) faulty nodes can be identified by Double-Syndrome diagnostic correctly.For given 2 syndromesσ1andσ2,there may exist some faulty nodes which cannot be identified by Double-Syndrome diagnostic.In next section,another diagnosable method is proposed to deal with these unidentified faulty nodes.

2 Two-step (k,t)-diagnosable system

For a system given byG=(V,E),under the assumption thatk-faulty nodes have been identified,it is a very interesting problem to recognize the remaining faulty nodes as much as possible.It is worth noting that with the different distribution of thek-identified nodes,the number of remaining faulty nodes which can be identified may be different[17].

Definition3A system is one-stept-diagnosable if all faulty nodes can be recognized without replacement provided the number of faulty nodes does not exceedt[3].

Definition4Given a system byG=(V,E) and a syndromeσ,a setX⊆Vis called an allowable fault set (AFS) of the system for syndromeσif for any 2 nodesi,jsuch that (i,j)∈E,the following conditions hold:ifi,j∈V-Xthenω(σ:i,j)=0,and ifi∈V-Xandj∈Xthenω(σ:i,j)=118.

It is worth noting that given a system byG=(V,E),a syndromeσand a fault setF,then there must exist an allowable fault setF′,such thatF⊆F′.In other words,there must exist a subsetS⊂Vsuch thatF∪Sis an allowable fault set for syndromeσ.

Definition5A system is two-step (k,t)-diagnosable if under the condition thatkfaulty nodes have been already recognized,the all remaining faulty nodes can be identified provided the number of faulty nodes in the system does not exceedk+t.

It is worth noting that according to Definition 3 and Definition 5,a one-step (k+t)-diagnosable system must be two-step (k,t)-diagnosable system,but the inverse is not true.Now an example is given which is two-step (k,t)-diagnosable but not one-step (k+t)-diagnosable.

Consider a systemG=(V,E) shown in Fig.1,it is a two-step (2,1)-diagnosable system.In fact,for any given syndromeσproduced by the system in the presence of the fault setFwith |F|≤3,if |F|≤2,then the conclusion is true according to the definition.We shall show it is also true when |F|=3.Now we only need to consider following 3 cases due to the symmetry of the system.LetFc⊂Fbe the possible identified faults set.

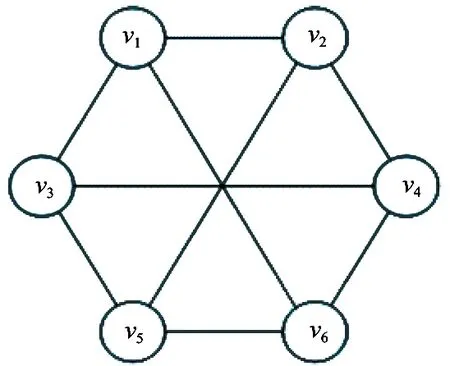
Fig.1 An example of a two-step (2,1)-diagnosable system

Case1Fc={v1,v2}.

There is only one faulty node in {v3,v4,v5,v6} and subgraph induced by {v3,v4,v5,v6} is connected.For the given syndromeσ,there always exist 2 adjacent nodesu,v∈{v3,v4,v5,v6} such that at least one ofω(σ:u,v) andω(σ:u,v) is 1.Then the faulty node belongs to {u,v} and {v3,v4,v5,v6}-{u,v}are all fault-free.Therefore,the remaining faulty node can be identified by the test results of their neighbors testing them.

Case2Fc={v1,v3}.

For any 2 adjacent nodesu,v∈{v4,v5,v6},ifω(σ:u,v)=0,thenv5is the remaining faulty node.Otherwise,v5is fault-free andv5can be identified correctly.Furthermore,v4,v6can also be identified correctly.

Case3Fc={v1,v4}.

Note that the subgraph induced by {v2,v3,v5,v6} is isomorphic to the subgraph induced by {v3,v4,v5,v6}.A similar argument of Case 1 can be used.

Above all,the system shown in Fig.1 is a two-step (2,1)-diagnosable system.However,it is not a one-step 3-diagnosable system due to the fact that |V|=6<2×3+1.

With the definition of the two-step (k,t)-diagnosable system,the characterization of this kind of system is presented.

Theorem1A system given byG=(V,E) is two-step (k,t)-diagnosable if and only if for each subsetFc⊂Vwith |Fc|=kand any 2 distinct subsets |S1|≤t,|S2|≤twith |S1|≤t,|S2|≤t,there exists an edge fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).

ProofNecessity:suppose that a system is two-step (k,t)-diagnosable,there exist someFc⊂Vwith |Fc|=kand some pair of subsetsS1,S2⊂V-FcwithS1≠S2,|S1|≤t,|S2|≤tsuch that there are no edges fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).Consider a syndrome σ such that for each (i,j)∈E:ifi,j∈V-S1-S2-Fc,thenω(σ:i,j)=0,ifi∈V-S1-S2-Fcandj∈Fc∪S1∪S2,thenω(σ:i,j)=1,other possible test results can be arbitrary.

For such syndromeσand the identified fault setFc,bothFc∪S1andFc∪S2are all allowable fault sets of cardinality at mostt+k,which is a contradiction to the hypothesis.

Sufficiency:suppose that,to the contrary,the system is not two-step (k,t)-diagnosable,implying that there exists a syndromeσby which ak-node fault setFccan be identified,and that there exist 2 distinct subsetsS1,S2⊂V-Fcof cardinality at mosttsuch thatFc∪S1andFc∪S2are allowable fault sets.Noting that there exists an edge fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).Without loss of generality,leti∈V-S1-S2-Fc,j∈(S1-S2) with (i,j)∈E.Ifω(σ:i,j)=1,thenFc∪S2is not an allowable fault set.Ifω(σ:i,j)=0,Fc∪S1is not an allowable fault set.This is a contradiction.

Note that two-step (k,t)-diagnosable system can be considered to be a generalization oft-diagnosable system,since ifk=0,two-step (k,t)-diagnosable system corresponds directly tot-diagnosable system.

Corollary1If a system is two-step (k,t)-diagnosable,then the system is also two-step (k,t-1)-diagnosable.

ProofAccording to Theorem 1,the result is true.

Corollary2If a system given byG=(V,E) is two-step (k,t)-diagnosable,then the system is also two-step (k-1,t)-diagnosable.

Corollary3If a system given byG=(V,E) is two-step (k,t)-diagnosable (k>2,t>1),then the system is also two-step (k-2,t+1)-diagnosable.

ProofAssume that,to the contrary,the system is not two-step (k-2,t+1)-diagnosable,thus,there exist a subsetFc⊂Vwith |Fc|=k-2 and a pair of subsetsS1,S2⊂V-FcwithS1≠S2,|S1|≤t+1,|S2|≤t+1,such that there are no edges fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).According to Lemma 1,the system is two-step (k-2,t)-diagnosable,implying that either |S1|≤t+1 or |S2|≤t+1.Consider the following cases.

Case4|S1|=t+1 and |S2|=t+1.

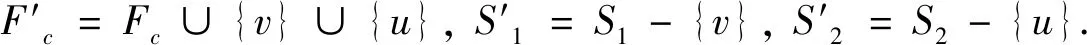
Case5|S1|≤tand |S2|=t+1.

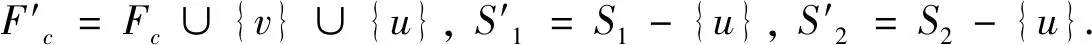
Case6|S1|=t+1 and |S2|≤t.

A similar argument of Case 6 can be used.

3 Two-step (k,t/t)-diagnosable system

In the previous section,the generalization oft-diagnosable system is discussed,namely the two-step (k,t)-diagnosable system.Next we shall consider the generalization oft/t-diagnosable system,namely the two-step (k,t/t)-diagnosable.

Definition6A systemSist/t-diagnosable if given any syndrome and a positive integert,the faulty nodes can be isolated within a set of at mosttnodes provided the number of faulty nodes does not exceedt[19].

Definition7A system is two-step (k,t/t)-diagnosable if and only if given any syndrome and a pair positive integerst,k,under the condition thatkfaulty nodes have been already identified correctly,all the remaining faulty nodes can be isolated within a set of size at mosttin the presence of at mostt+kfaulty nodes in all.With the definition of the two-step (k,t/t)-diagnosable system,we shall present the characterization of this kind of system.

Theorem2For a systemSgiven byG=(V,E),the following 3 statements are equivalent.

1)Sis two-step (k,t/t)-diagnosable.

2) For each subsetFc⊂Vwith |Fc|=kand for any 2 distinct subsetsS1,S2⊂V-Fcwith |S1|=|S2|=t,there exists an edge fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).

3) For each subsetFc⊂Vwith |Fc|=kand for any 2 distinct subsetsS1,S2⊂V-FcwithS1⊄S2,S2⊄S1,|S1|≤t,|S2|≤t,there exists an edge fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).

ProofThe proof is similar to the proof of Lemma 1 in Ref.[10].

According to Theorem 6,the following corollaries can be concluded.

Corollary4If a system given byG=(V,E) is two-step (k,t/t)-diagnosable,then the system is also two-step (k,t-1/t-1)-diagnosable.

Corollary5If a system given byG=(V,E) is two-step (k,t/t)-diagnosable,then the system is also two-step (k-1,t/t)-diagnosable.

Corollary6If a system given byG=(V,E) is two-step (k,t/t)-diagnosable,then the system is also two-step (k-2,t+1/t+1)-diagnosable.

Next section will analysis the specific situation by using the theories of two-step (k,t)-diagnosable system and two-step (k,t/t)-diagnosable system.

4 Combine to the Double-Syndrome diagnostic

For a system given byG=(V,E) and a fault setFcidentified by Double-Syndrome diagnostic with |Fc|=k,if there exists a nodev∈Vsuch thatΓv-1⊆Fc,then the nodevcannot be judged as faulty or fault-free.Therefore,whether all the remaining faulty nodes can be identified or not depends on the distribution ofFc.Next it will be discussed that with the changes of distribution ofFc,how many remaining faulty nodes can be identified.

Definition8For a two-step (k,t)-diagnosable systemSand a fault setFcidentified by Double-Syndrome diagnostic or other methods,the diagnosability of the two-step (k,t)-diagnosable based onFc,denoted byT(S,Fc),is the maximum number of nodes which is guaranteed to be identified as faulty correctly.To facilitate the discussion,the following theorem is equivalent to Theorem 1.

Theorem3For a system given byG=(V,E) and a fault setFc⊆Vwith |Fc|=k,then all the remaining faulty nodes at mosttcan be identified if and only if for any 2 subsetsS1,S2⊂VwithS1≠S2,|S1|≤t,|S2|≤tsuch thatΓ(S1-S2)-1⊄Fc∪S2orΓ(S2-S1)-1⊄Fc∪S1.

Corollary7For a system given byG=(V,E) and a fault setFcwith |Fc|=k,if for each subsetU⊂V-Fcwith |U|≤2t,there exists no such subsetX⊆Usuch thatΓX-1⊆Fc∪(U-X),then all the remaining faulty nodes can be identified provided the number of remaining faulty does not exceedt.

ProofFor any distinct subsetsS1,S2⊆Vwith |S1|≤t,|S2|≤t,letU=S1∪S2andX=(S2-S1)∪(S1-S2).ifΓX-1⊄(Fc∪(U-X)),then it is easily seen that the condition of the Theorem 1 is satisfied.

The following theorem is equivalent to Theorem 2.

Theorem4For a system given byG=(V,E) and a fault setFcwith |Fc|=k,all remaining faulty nodes at mosttcan be isolated within a set of size at mosttif and only if for any 2 subsetsS1,S2⊂V-FcwithS1⊄S2,S2⊄S1,|S1|≤t,|S2|≤t,such thatΓ(S1-S2)-1⊄Fc∪S2orΓ(S2-S1)-1⊄Fc∪S1.

Corollary8For a system given byG=(V,E) and a fault setFcwith |Fc|=k,if for each subsetS⊂Vwith |S|≤2t,there exists no such a subsetX⊆Ssuch thatΓX-1⊆Fc∪(S-X),then all remaining faulty nodes can be isolated within a set of size at mosttprovided the number of remaining faulty does not exceedt.

A similar proof of Corollary 7 can be used.

Observe above theorems and corollaries,when the neighbors of some nodes are all faulty,it cannot be correctly identified such a node.Therefore the following conclusion.

Theorem5For a systemSgiven byG=(V,E),ifSist′-diagnosable(but nott′+1-diagnosable) and also two-step (k,t)-diagnosable(but neither two-step (k,t+1)-diagnosable nor two-step (k+1,t)-diagnosable) (t′≥k)),then its diagnosability satisfies the following inequality:T(S,Fc)≥t′ whereFc⊆Vand |Fc|=k.

ProofAccording to Definition 4 and Definition 8,for any given fault setFc⊆Vwith |Fc|=k,T(S,Fc)≥t+k.Next,it can be shown thatt+k≥t′.Otherwise,t+kt′,this is a contradiction.

Note that the number of fault-free neighbors of each node is related to the diagnosability of kinds of diagnosable systems[20,21].Ref.[20] considered the situation that each node has at least one fault-free neighbor in the system and proposed the concept of conditional diagnosability.The next section will extend the concept of conditional diagnosability to two-step (k,t)-diagnosable ((k,t/t)-diagnosable) system and present the characterizations of conditional two-step (k,t)-diagnosable (((k,t/t)-diagnosable) systems.

5 Conditional two-step (k-t)-diagnosable and two-step (k,t/t)-diagnosable

The hypercube structure is a well-known network model for multi-processor systems.Fault-tolerant computing forn-dimensional hypercube has been of interest to many researchers[17-19,21].In this subsection,the conditionalt/t-diagnosability ofn-dimensional hypercube is studied.

Definition9For a system given byG=(V,E),a subsetS⊂Vis called a conditional subset if there exists no such a nodev∈Vsuch thatΓv-1⊆S.

Lemma2A system given byG=(V,E) is conditionallyt-diagnosable if and only if for any 2 conditional subsetsS1,S2⊆VwithS1≠S2,|S1|≤t,|S2|≤t,there exists an edge fromV-S1-S2to (S1-S2)∪(S2-S1)[22].

Definition10A system is conditionally two-step (k,t)-diagnosable under the condition thatkfaulty nodes have been already recognized,and all the remaining faulty nodes can be identified provided the number of faulty nodes in the system does not exceedk+tand each node of the system has at least one fault-free neighbor.

Theorem6A system given byG=(V,E) is conditional two-step (k,t)-diagnosable if and only if for any conditional subsetFcwith |Fc|=kand any 2 conditional subsetsS1,S2⊂V-FcwithS1≠S2,|S1|≤t,|S2|≤t,Fc∪S1andFc∪S2are conditional subsets,there exists an edge fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).

ProofNecessity:suppose that a system is conditional two-step (k,t)-diagnosable and for some conditional subsetFcwith |Fc|=kand 2 conditional subsetsS1,S2⊂V-FcwithS1≠S2,|S1|≤t,|S2|≤t,Fc∪S1andFc∪S2are conditional subsets,there exists no edge fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).Consider a syndromeσsatisfying the following conditions for all nodesi,jsuch that (i,j)∈E.Ifi,j∈V-S1-S2-Fc,thenω(σ:i,j)=0.Ifi∈V-S1-S2-Fcandj∈S1∪S2,thenω(σ:i,j)=1.Ifi∈(S1-S2)∪(S2-S1) andj∈Fc∪(S1∩S2),thenω(σ:i,j)=1.Other possible test results can be arbitrary.

According to Definition 3,thatS1andS2are all allowable fault sets.Therefore,it cannot be identified that which one is the real fault set which is a contradiction to the hypothesis.

SufficiencySuppose that,to the contrary,the system is not conditional two-step (k,t)-diagnosable.Thus,there exist a conditional subsetFc⊆Vwith |Fc|=kand 2 conditional subsetsS1,S2⊂VwithS1≠S2,|S1|≤t,|S2|≤t,andFc∪S1andFc∪S2are conditional subsets,such thatFc∪S1andFc∪S2are all allowable fault sets.Noting that there exists an edge fromV-S1-S2-Fcto (S1-S2)∪(S2-S1).Without loss of generality,leti∈V-S1-S2-Fc,j∈(S1-S2) with (i,j)∈E.For a syndromeσ,ifω(σ:i,j)=1,thenS2is not an allowable fault set,otherwise,S1is not an allowable fault set which is a contradiction to the hypothesis.Similarly,j∈(S1-S2) also leads to a contradiction to the hypothesis.

Definition11For a conditionally two-step (k,t)-diagnosable systemSand a fault setFcidentified by Double-Syndrome diagnostic or other methods,the diagnosability of the conditionally two-step (k,t)-diagnosable systems based onFc,denoted byTc(S,Fc),is the maximum number of nodes that are guaranteed to be identified as faulty correctly.

Theorem7For a systemSgiven byG=(V,E),ifSis conditionallyt′-diagnosable(but not conditionallyt′+1-diagnosable) and also conditionally two-step (k,t)-diagnosable(but neither conditionally two-step (k,t+1)-diagnosable nor conditionally two-step (k+1,t)-diagnosable) (t′≥k)),then its diagnosability satisfies following inequality:Tc(S,Fc)≥twhereFc⊆Vand |Fc|=k.

ProofA similar argument of Theorem 5 can be used.

Lemma3Suppose that an undirected graphG=(V,E) denotes a system and that each node inG=(V,E) has at least one fault-free neighbor.For any setS⊂Vwith |S|≤3,ifN(S) are all faulty nodes,then each node ofScan be identified correctly.

ProofLet |S|=mandS={vi:1≤i≤m}.Now discuss the following cases:

Case7m=2.

It is obvious that ifv1(v2) is faulty,thenN(v2)(N(v1)) is all faulty nodes which is a contradiction to the condition.Therefore,v1,v2are all fault-free.

Case8m=3 andScan form a cycle.

There is at most 1 faulty node inS.Otherwise,there are at least 2 faulty nodes inS,without loss of generality,assume thatv1,v2are faulty nodes,thenN(v3) are all faulty nodes which contradict the assumption.It is easy to judge the state(faulty or fault-free) of each node by observing the syndrome.

Case9m=3 andScannot form a cycle.

Since each node has at least one fault-free neighbor andN(S) are all faulty nodes,Sis connected.The middle nodev2ofSis fault-free,otherwise,N(v1) andN(v3) are all faulty nodes,which is a contradiction to the assumption.Furthermore,the other 2 nodes can be identified correctly.

5.1 n-dimensional hypercube

Lemma5n-dimensional (n≥5) hypercube is conditional [4(n-2)+1]-diagnosable[20].

Next,then-dimensional (n≥5) hypercube given byG=(V,E) is not conditional [4(n-2)+1]-diagnosable.LetS={v0,v1,v2,v3} whereScan form a cycle andS1=N(S)∪{v0,v1},S2=N(S)∪{v2,v3}.Note that |N(S)|=4(n-2) andS1=S2=4(n-2)+2.For subsetsS1,S2,there exists no such a nodevthatN(v)⊆S1orN(v)⊆S2.And for subsetsS1,S2,there exists no edge fromV-S1-S2to (S1-S2)∪(S2-S1).Therefore,the system is not conditional [4(n-2)+2]-diagnosable.

Note that if a system ist-diagnosable,then such system must bet/t-diagnosable[23].Therefore,n-dimensional (n≥5) hypercube given byG=(V,E) is conditional (4n-7)/(4n-7)-diagnosable[24].Furthermore,then-dimensional (n≥5) hypercube given byG=(V,E) is not conditional (4n-6)/(4n-6)-diagnosable.

Theorem8n-dimensional (n≥5) hypercube is not conditional (4n-6)/(4n-6)-diagnosable.

ProofLetS={v0,v1,v2,v3} whereScan form a cycle andS1=N(S)∪{v0,v1},S2=N(S)∪{v2,v3}.Note that |N(S)|=4(n-2) andS1=S2=4(n-2)+2.Now consider following syndromeσunder the condition that all nodes ofN(S) are faulty.

1) The test results fromStoN(S) are 1.

2)ω(σ:v0,v1)=0,ω(σ:v1,v0)=0,ω(σ:v2,v3)=0,ω(σ:v3,v2)=0,ω(σ:v1,v2)=1,ω(σ:v2,v1)=1,ω(σ:v0,v3)=1,ω(σ:v3,v0)=1.

3) The other possible test results are arbitrary.

For above syndromeσ,the system cannot isolate all faulty nodes within a set of size at most 4n-6.Therefore,then-dimensional (n≥5) hypercube is not conditional (4n-6)/(4n-6)-diagnosable.

5.2 Permutation star graph

Lemma6LetG=(V,E) be the graph of a star graph ofn(n≥4) dimension andX⊆Vwith |X|=8 andXcan form an 8-node ring,then |N(X)|=8n-24.

ProofAccording to the symmetry of star graph,each 8-node ring inn(n≥4) dimensional star graph is equivalent.Therefore,consider following case as Fig.2,the 1234A representsn-bit position ofv1andAis a (n-4)-bit position which consists of 5,6,…,n.Letadd(v,i,j) be the address of nodevfrom numberibit to numberjbit.Note that in Fig.2,add(vi,2,4)≠add(vj,2,4) wherei,j∈[1,2…,7] andi≠j.Therefore,for each node of Fig.2,it has (n-4) private neighbors.Note that each node ofn-dimensional star graph has (n-1) adjacent nodes and for each node of an 8-node ring,for example,v1has 2 adjacent nodes in the ring andn-4 private neighbors outside the ring.Then the address of the last neighbor ofv1is 2134A which shows that last neighbor ofv1is also the private neighbor ofv1.Similarly,the last neighbor of nodev2(v3…v8) is also their private neighbors.Thus,each node of an 8-node ring hasn-3 private neighbors and letXbe an 8-node ring,then |N(X)|=8n-24.

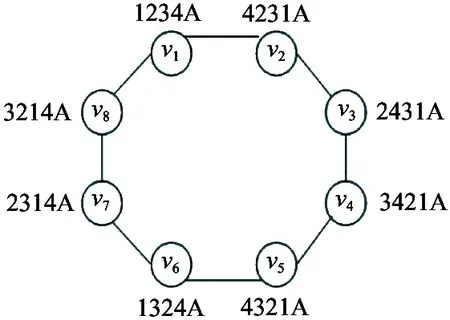
Fig.2 An 8-node ring of n-dimensional star graph

Lemma7In ann-dimensional star graph,there are no odd cycles and there are even cycles with lengthlwherel≥6，l≤n[25].

Lemma8In ann-dimensional star graph,letube a node and letu1,u2…un-1ben-1 neighbors of it[22].Then every pairui,ujand nodeuform a loop with 3 other nodes which are unique.

Lemma9n-dimensional (n≥5) star graph given byG=(V,E) is conditional [8(n-3)+3]-diagnosable[26].Secondly,then-dimensional (n≥5) star graph given byG=(V,E) is not conditional (8n-20)-diagnosable.

Theorem9n-dimensional (n≥5) star graph given byG=(V,E) is not conditional (8n-20)-diagnosable.

ProofLetS={v1,v2,v3,v4,v5,v6,v7,v8} whereScan form a cycle in the clockwise andS1=N(S)∪{v1,v2,v5,v6},S2=N(S)∪{v3,v4,v7,v8}.Note that according to Lemma 9,|N(S)|=8n-24 and |S1|=|S2|=8n-20.For subsetsS1,S2,there exists no such a nodevthatN(v)⊆S1orN(v)⊆S1.And for subsetsS1,S2,there exists no edge fromV-S1-S2to (S1-S2)∪(S2-S1).Therefore,the system is not conditional (8n-20)-diagnosable.

Theorem10n-dimensional (n≥5) star graph given byG=(V,E) is not conditional (8n-20/8n-20)-diagnosable.

ProofLetS={v1,v2,v3,v4,v5,v6,v7,v8} whereScan form a cycle in the clockwise andS1=N(S)∪{v1,v2,v5,v6},S2=N(S)∪{v3,v4,v7,v8}.Note that according to Lemma 9,|N(S)|=8n-24 and |S1|=|S2|=8n-20.Now consider following syndromeσunder the condition that all nodes ofN(S) are faulty.

1) The test results fromStoN(S) are 1.

2)ω(σ:v1,v2)=0,ω(σ:v2,v1)=0,ω(σ:v3,v4)=0,ω(σ:v4,v3)=0,ω(σ:v5,v6)=0,ω(σ:v6,v5)=0,ω(σ:v7,v8)=0,ω(σ:v8,v7)=0,ω(σ:v2,v3)=1,ω(σ:v3,v2)=1,ω(σ:v4,v5)=1,ω(σ:v5,v4)=1,ω(σ:v6,v7)=1,ω(σ:v7,v6)=1,ω(σ:v1,v8)=1,ω(σ:v8,v1)=1.

3) The other possible test results are arbitrary.

For above syndromeσ,the system cannot isolate all faulty nodes within a set of size at most 8n-20.Therefore,then-dimensional (n≥5) star graph is not conditional (8n-20/8n-20)-diagnosable.The following is shown as Algorithm 2 and Algorithm 3.

Algorithm2Double-Syndromeconditionaldiagnosis: part1Algorithm:majorneighbor:Require: AsystembyundirectedgraphG=(V,E)withNnodesdenotedby{u1,u2,…,uN}andasubsetFc⊆Vwith|Fc|=kandai=0(1≤i≤n).Ensure: AsetNFc. 1)Foreachnodevi∈V(0≤i≤k-1),ifuj∈N(vi)(1≤j≤n),thenaj=aj+1. 2)LetNFc={ui|ai≥ajwhere1≤j≤n}. 3)OutputthesetNFc.Algorithm:depth-firstsearch:Require: AsystemgivenbyundirectedgraphG=(V,E)withNnodesandanodev∈V.LetS={v}.Ensure: SeveralnodesetsMi(1≤i≤N). 1)DFS(v): Foreachu∈N(v) Ifw(u,v)=w(v,u)=0. S=S∪{u}andDFS(u). 2)OutputthenodessetS.Algorithm:testneighbor:Require: AsystemgivenbyundirectedgraphG=(V,E)withNnodesandasubsetX⊆VandthreesetsT,FcandM.LetS={v}.Ensure: ThesetT,FcandM. 1)Test(X,T,Fc,M) Foreachnodeofu∈N(X) IfthetestresultfromutoN(X)is0,thenT=T∪{u}andtest({u},T,Fc).OtherwiseFc=Fc∪{u}andM=M-{u}. 2)OutputthesetsT,FcandM.Algorithm:testcomponent:Require: AsystemgivenbyundirectedgraphG=(V,E)withNnodesandthreesetsT,FcandM.Ensure: ThesetT,Fc.

Testcomponent(T,Fc,M): 1)Foreachnodew∈M,ifthereexistsanodex∈MsuchthatN(x)∩M={w},thenT=T∪{w}andTest({w},T,Fc,M). 2)Ifthereexist3nodesu,v,w∈Msuchthatthetestresultsofthemareall0,thenT=T∪{u,v,w}andTest({u,v,w},T,Fc,M). 3)Ifthereexist2pairadjacentnodes{u,v},{w,x}∈Msuchthatthetestresultsofu,v(andw,x)areall0,thenT=T∪{u,v,w,x}andtest({u,v,w,x},T,Fc,M). 4)Repeatstep1)tostep3),untilV=T∪Fc.OutputthesetT,Fc.

Algorithm3Double-Syndromeconditionaldiagnosis:part2Require: AsystemgivenbyundirectedgraphG=(V,E)withNnodesandafaultnodesetFc⊆Vwith|Fc|=kobtainedfromDouble-Syndromediagnosticorothermethods.Andafaultboundt(thatthesystemisconditionalt-diagnosable).Ensure: AfaultynodesetFcandafault-freenodessetT(T∪Fc=V). 1)NFc=majorneighbor(G,Fc). 2)Foreachnodeui∈V-∪ij=1Sj-Fc(ui∈NFcisapriority). DoDFS(ui). Si=DFS(ui) If|Sj|≥t-|Fc|+1,where1≤j≤i. T=T∪SjandFc=Fc∪N(T). 3)IfV=T∪Fc,thenoutputthefault-freenodesetTandfaultynodessetFc.Otherwisegotostep4). 4)LetM=V-T-FcandM={Ci|CiisacomponentofM}. Testcomponent(T,Fc,M). Outputthefault-freenodessetTandthefaultynodessetFc.

5.3 Algorithms for conditional two-step (k,t)-diagnosable systems

In the following,a diagnosis algorithm is proposed called Double-Syndrome conditional diagnosis(DSCD) which combines Double-Syndrome diagnostic and the theories of conditional two-step (k,t)-diagnosable system.

Consider step 4) in Algorithm 3,the neighbors of the nodes of setMare all faulty.Note that inn-dimensional hypercube,|M|≤4 with at most one faulty node,inn-dimensional star graph,|M|≤8 with at most 3 faulty nodes.A similar argument of Lemma 3 can prove the rightness of step 4) in Algorithm 3.

Theorem11The algorithm DSCD has a time complexityO(Nlog2N),whereNis the number of the nodes of the system.

ProofIn Algorithm 3,step 1) costsO(kn) time.Step 2) costsO(Nlog2N)+O(N) time.Step 3) and 4) costsO(1) time.Hence the total time isO(Nlog2N).

Now the performance of the algorithm by computer simulation is shown below.Run the algorithm 1 000 times and the faulty nodes are randomly distributed in the system.Table 2 and Table 3 show the performance of this algorithm applied ton-dimensional hypercubes and star graphs.

Table 2 The number of faulty nodes identified by the algorithm under the n-dimensional hypercube

Table 3 The number of faulty nodes identified by the algorithm under the n-dimensional star graph

6 Conclusions

Under PMC model,a new method is proposed,which is called Double-Syndrome diagnostic to diagnosis the faulty nodes by comparing the 2 syndromes.In general,the average number of faulty nodes which can be identified by Double-Syndrome diagnostic is much larger than other methods.Furthermore,for a given faulty node setFc,in order to deal with the remaining faulty nodes in the system,two-step (k,t)-diagnosable strategy and two-step (k,t/t)-diagnosable strategy are proposed.For a givent′-diagnosable system,its two-step (k,t)-diagnosability has a minimum value which is equal tot′.Meanwhile,with the purpose of increasing the diagnosability,the concept of conditional two-step (k,t)-diagnosable system and the concept of conditional two-step (k,t/t)-diagnosable system are proposed.Similarly,for a given conditionallyt′-diagnosable system,the conditional two-step (k,t/t)-diagnosability has a minimum value which is equal tot′.