油页岩固定床干馏过程三维数值模拟
华泽嘉, 王 擎, 蒋佳奇
(1.华北电力大学能源动力与机械工程学院, 北京 102206; 2.东北电力大学能源与动力工程学院, 吉林 132012)
油页岩又称油母页岩,是一种以无机矿物质为骨架,内含固体有机质的沉积岩,作为固体化石燃料,与煤、石油、天然气一样均为不可再生化石能源。油页岩储存量丰富,具备作为传统化石燃料替代能源的巨大潜力和条件[1-3]。目前中外利用油页岩提取燃料的处理方式主要有两种:分别应用固体热载体和气体热载体为热源的干馏炉干馏工艺。在油页岩气体热载体干馏工艺中,使用最为广泛的是固定床干馏工艺,如抚顺式干馏炉、佩特洛瑟克斯炉、鲁奇加压气化炉、苏联基维特炉等[4-5]。
由于固定床内的通道有限,因此对固定床的实验研究通常很难进行。采用数值模型作为补充方法对其进行研究,可以更深入地了解固定床内相关过程的具体细节。许多学者对固定床干馏及相关过程的实验和模拟做了大量研究,Izadifar等[6]采用体积平均方法对稻谷的干燥过程进行研究,并与实验数据进行了比较,其中稻谷的干燥模型中蒸发速率是温度和相对湿度的函数,并将偏离实验数据的情况归因于局部热平衡假设,由于这个假设导致水分含量和颗粒内部的温度梯度可以忽略不计。以同样的方式,Assari等[7]忽略了颗粒内部温度和相对湿度的梯度,将蒸发速率作为颗粒温度和水分含量的函数进行计算,对流化床中的干燥过程进行预测,并与实验结果进行比较,得出尽管固体温度与实验结果非常接近,但固体颗粒的水分含量相差较大。Yang等[8-12]从实验和模拟两个方面研究了燃料粒径、含水量、脱挥发分过程、一次空气流率对失重速率、床内温度和烟气中气体组分的影响。Na等[13]通过建立固定床干燥和热解数学模型,考察水分含量和干燥温度对木材的干燥和热解过程的影响。常用的干燥模型主要有以下几种:恒定蒸发模型(heat sink model)[14-18],一阶动力学模型(first order evaporation rate model)[19-20]和均衡模型(equilibrium model)[21]。Collazo等[22]发现当采用恒定蒸发模型时,在一个时间步长内允许颗粒的温度增加到超过干燥温度的上限,超出的热量用于水分的蒸发。因此,在每一个时间步内的干燥过程中,颗粒接收的热量一部分用于水分的蒸发,其余的热量用来加热颗粒的温度。许多学者对油页岩的热解机理进行了相关的研究[23-27],但由于油母质本身的分子结构尚未弄清,而其热解过程十分复杂,故油母质的热解机理至今只是宏观的,半经验半理论性的,因此现选用一步整体反应模型来描述热解反应中挥发分析出的过程。
目前,许多工作将固定床考虑为零维、一维和二维模型,完整的三维模型仍处于发展阶段。现旨在建立固定床内油页岩干馏过程的三维数学模型,对固定床内气相和固相间的传热和传质过程进行详细分析。将实验工况下的模拟结果与测量结果进行对比验证,并从进气速度和进气温度等方面对油页岩干馏过程的影响规律进行深入研究。
1 数学模型的建立
1.1 水分析出过程
油页岩干馏过程前期必然先经过一个脱去内水的过程,含水固体颗粒在固定床反应器内首先因热载体加热而发生水分蒸发。页岩原料通常含有1%~2%的结合水,在一定的温度区间内,假设这种结合水随温度的升高呈线性变化[28],因此,选择恒定蒸发模型计算蒸发速率,具体表达式为
R1=U1RT/(TH-TL)
(1)
式(1)中:R1为反应速率;U1为油页岩中初始水分浓度;TL为反应起始温度;TH为反应上限温度;RT为页岩颗粒升温速率,计算式为
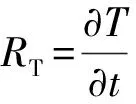
(2)
式(2)中:T为温度;t为时间。
1.2 干馏过程
油页岩的干馏过程是在无氧或缺氧条件下进行的干酪根受热分解过程,反应生成的气体主要包括页岩油蒸汽、CO、CO2、H2、CHx和其他微量成分。由于热解过程的复杂性,详细的动力学过程尚不清楚,现采用一步整体反应模型来描述干酪根热解过程中热解气体的析出过程:
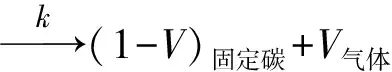
(3)
式(3)中:V为热解气体产物所占的份额;k为颗粒热解速率,其表达式为
k=Aexp[-E/(RT)]
(4)
式(4)中:A为指前因子;E为活化能;R为通用气体常数;T为温度。详细动力学参数如表1所示。

表1 热解反应动力学参数Table 1 Pyrolysis reaction kinetic parameters
1.3 气相控制方程
采用以下假设对固定床内热解过程进行模拟:①气体热载体为理想气体;②固定床内颗粒堆积区域为三维多孔介质;③固定床壁面为绝热壁面。
1.3.1 质量守恒方程
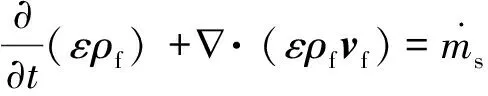
(5)

1.3.2 动量守恒方程
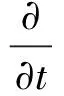
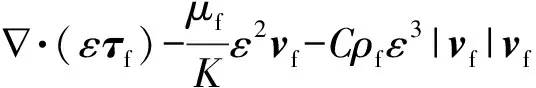
(6)
式(6)中:μf为气体动力黏度;τf为应力张量;K为床层渗透率,C为阻力系数,这两个参数都可以从相关固定床的经验关联式中得到[29-31],是颗粒直径Dp和孔隙率ε的关联式,如式(7)、式(8)所示。

(7)

(8)
1.3.3 能量守恒方程
λfε2Tf+hsfA(Ts-Tf)+STf
(9)
式(9)中:STf为水分蒸发和干酪根热解时引起的气相中热量变化;cpf为气相比热;λf为气相导热系数;Ts为固相温度;Tf为气相温度;hsf为气固两相间的换热系数[32],计算式为
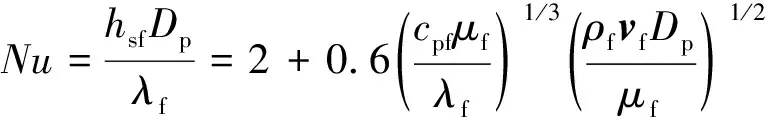
(10)
1.3.4 组分输运方程
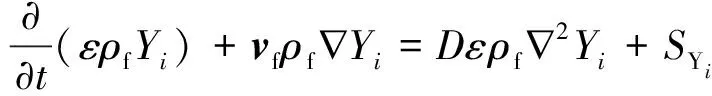
(11)
式(11)中:Yi为组分质量分数;D为扩散系数;SYi为水分蒸发和干酪根热解时引起的质量变化。
1.4 固相控制方程
1.4.1 质量守恒方程
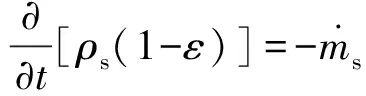
(12)
式(12)中,ρs为固相密度。
1.4.2 能量守恒方程
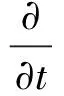
λs(1-ε)2Ts+hsfA(Tf-Ts)+STs
(13)
式(13)中:STs为水分蒸发和干酪根热解时引起的固相中热量变化;cps为固相比热;λs为固相导热系数。其中,气相和固相求解的边界条件为
Tf|t=0=(Tf)in
(14)
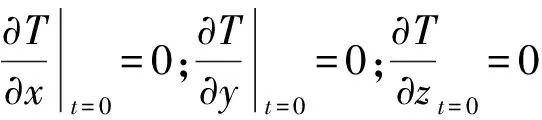
(15)
2 物理模型与模型验证
图1所示为本文工作采用的物理模型及网格划分情况。固定床整体高度为4 000 mm,直径为500 mm,为了研究固定床内颗粒的干馏过程,固定床可分为由气体热载体和油页岩颗粒混合的多孔介质区域以及气体区域,其中颗粒堆积高度为2 400 mm。从固定床底部进气面通入一定质量流量的高温甲烷气体用来加热固定床内的物料。表2给出了本文模拟工作所用的相关物性参数及边界条件。

图1 物理模型及网格划分Fig.1 Physical model and meshing
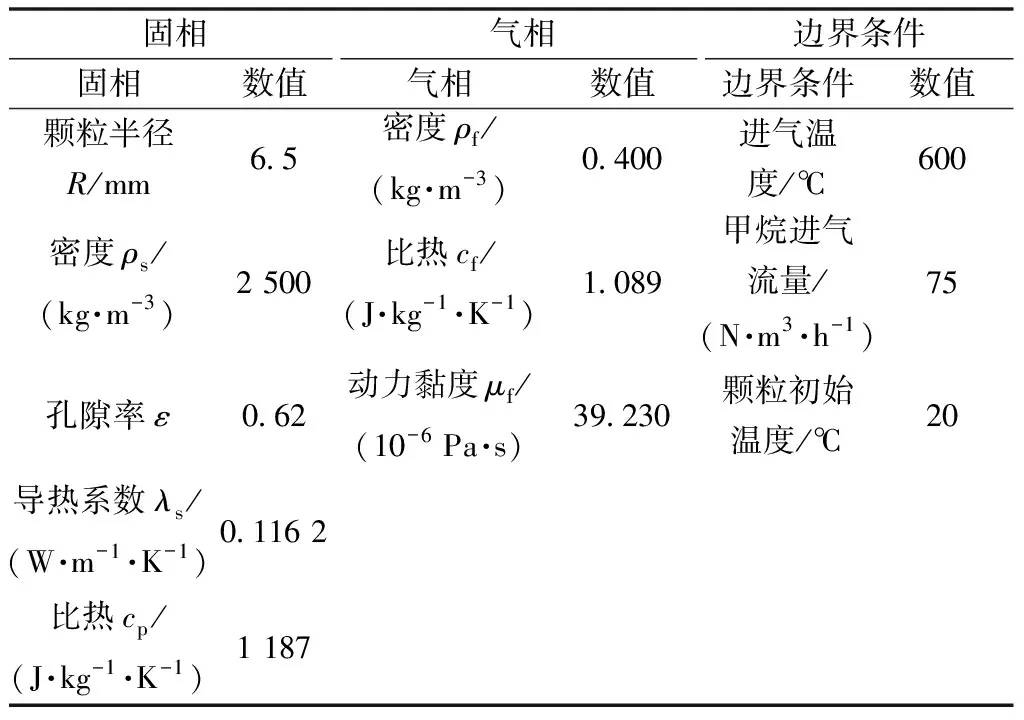
表2 物性参数及边界条件Table 2 Physical parameters and boundary conditions

图2 平均温度模拟结果与实验结果对比Fig.2 Comparison of average temperature simulation results with experimental results
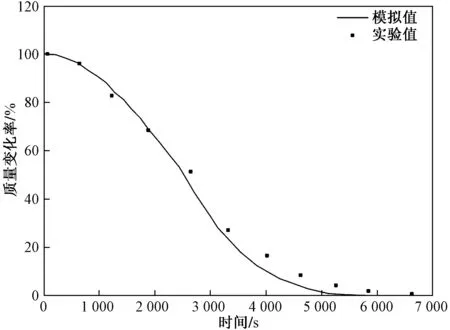
图3 质量变化率模拟结果与实验结果对比Fig.3 Comparison of mass change rate simulation results with experimental results
图2给出了应用固定床数值模型对不同床层高度下气体温度分布的预测情况,并将模拟值与实验值绘制于图中。从图2中可以观察到,气体温度逐渐升高最终达到入口气体温度,底层的气体温度高于上层,气体温度沿高度方向变化显著,模拟值与实验值吻合程度较高。图3给出了在干馏过程中,由于干酪根受热分解所导致的颗粒整体质量变化的模拟值与实验值的对比情况。可以看出,模拟结果与实验结果取得较好的吻合性。因此,本文所采用的数值模型能够对固定床内干馏过程进行合理的预测。
3 结果与讨论
3.1 基于实验工况下的详细模拟结果
入口气体温度为600 ℃,入口气体流速为3.0 m/s,油页岩颗粒半径为6.5 mm,固定床内油页岩颗粒堆积高度为2 400 mm。基于以上运行参数,图4分别给出了不同时刻下气相和固相平均温度的分布情况,不同时刻下固体中水分含量分布情况,以及不同时刻下固相中干酪根含量分布情况。由图4可知,在初始的100 s内,由于气体热载体温度较高,导致短暂的接触后,率先发生接触的固体颗粒已被加热,底部颗粒的平均温度高于其他位置的固体平均温度。

图4 气相和固相平均温度Fig.4 Gas and solid phase average temperature
图5所示为固相中的水分含量,可知,在0~100 s内,底部颗粒温度已被加热到水分蒸发的起始温度,在此时间段内伴随着水分的析出过程。

图5 固相中水分含量Fig.5 Moisture content in the solid phase
图6所示为固相中的干酷根含量,可知,在300 s左右时,底部颗粒吸收的热量达到干酪根热解反应的起始条件,并伴随着热解气体的析出过程。由图6可知,在0~2 500 s内,由于气体热载体与颗粒之间的热量交换,颗粒接收的热量一部分用于颗粒内部水分的蒸发,其余的热量用于干酪根的热解。因此,在达到颗粒堆积区域的出口之前,入口气体热载体已将全部热能消耗掉,这使得颗粒堆积区域顶部几乎处于最低的颗粒温度。但在3 000 s时,顶部和底部颗粒之间的温差逐渐减小,这是由于底部和中部区域的颗粒中水分已经全部析出,大部分干酪根完全热解,使得此区域内的颗粒温度逐渐接近入口气体温度,因此在气体到达顶部的时候,能够利用剩余的热能与顶部的颗粒进行换热。
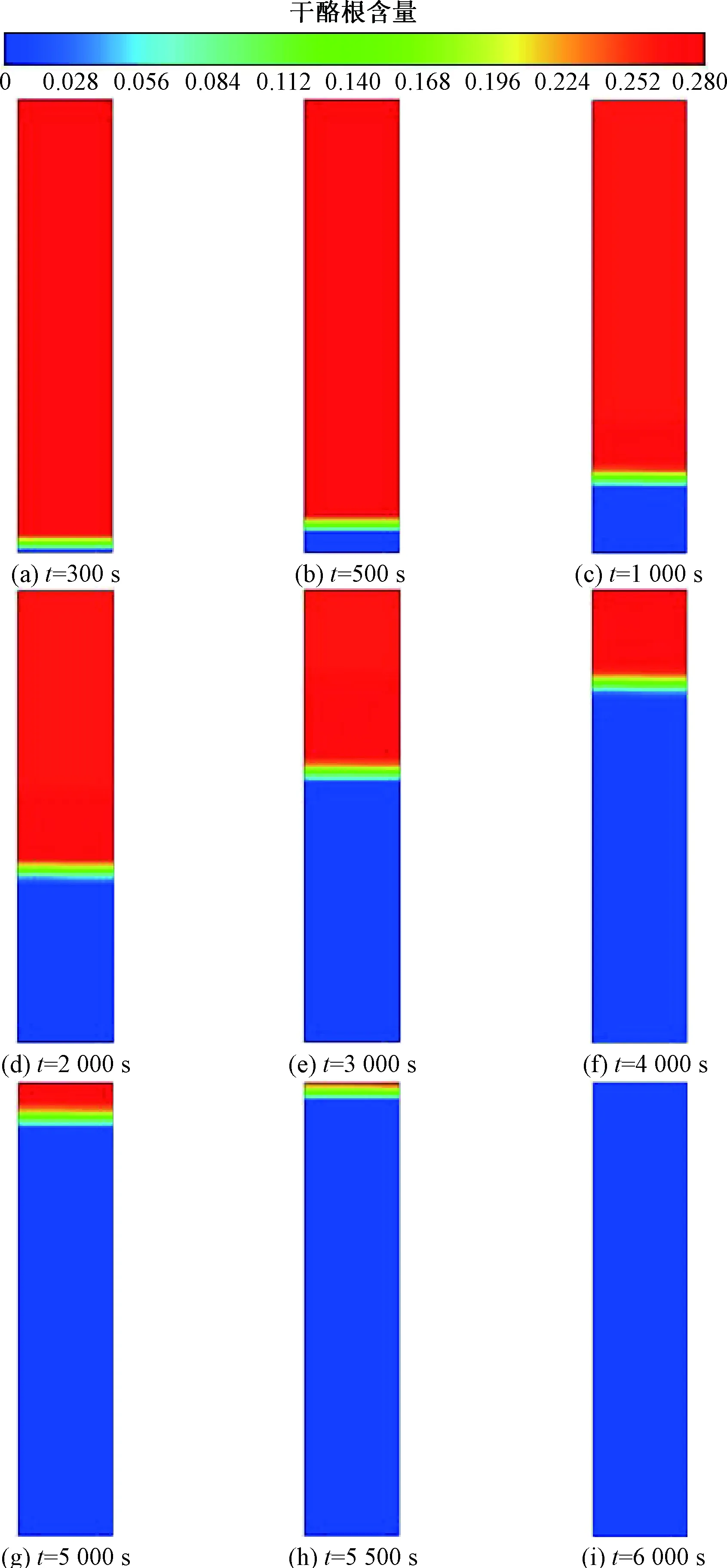
图6 固相中干酪根含量Fig.6 The kerogen content in the solid phase
图7为颗粒堆积区域底部、中部和顶部区域的颗粒温升情况。图8为固定床内颗粒整体升温情况。结合图8可知,在4 000 s时,颗粒中的水分已经全部析出,此时反应主要为固相中干酪根的热解。由于固定床内颗粒整体温度仍在上升,系统还没有达到稳定状态,因此出口处的气体温度低于入口气体温度。在6 000 s时,固相中干酪根的热解反应结束,并随着时间的推移,系统内部达到稳定状态,此时固定床内整体温度达到气体热载体温度。

图7 不同高度下颗粒的平均温度Fig.7 Average temperature of particles at different heights
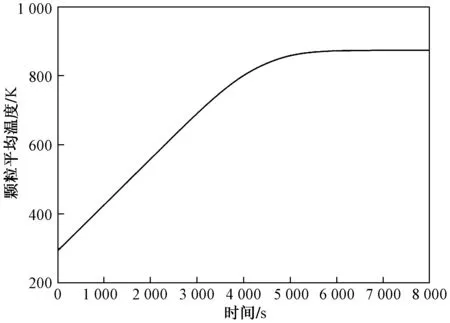
图8 颗粒整体温升情况Fig.8 Overall temperature rise of the particles
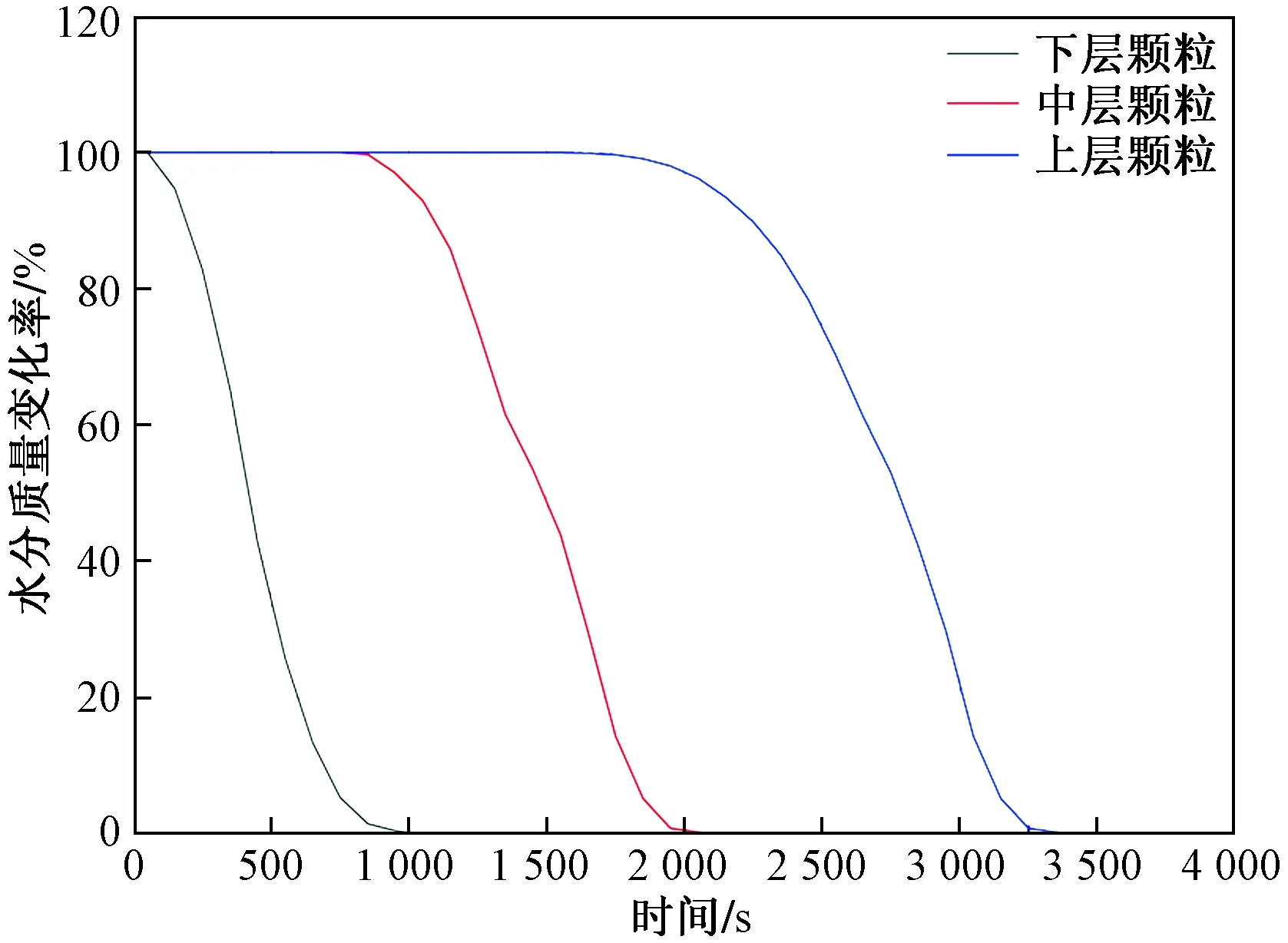
图9 颗粒中的水分含量Fig.9 Water content in the granules

图10 颗粒中的干酪根含量Fig.10 Kerogen content in the granules
为了更好地了解固定床内油页岩干馏过程的细节,图9~图12分别给出了颗粒堆积区域底部、中部及顶部颗粒中的水分含量、干酪根含量、水蒸气质量分数和热解气体质量分数随时间变化的情况。由图9可知,在水分析出过程的尾声时,可以看到曲线存在一个小的阶跃,这是由于颗粒表层水分全部析出,表层温度随之上升,从而提高颗粒的平均温度。
类似于图9,在图10所示的干酪根热解过程尾声时,仍可以观察到这些曲线的跳跃但并不明显。这是因为在干酪根热解过程末段,颗粒已经吸收了足够的热能,当反应结束时,颗粒表层的温度与气体热载体之间的温差较小,因此颗粒温度的瞬时提高对颗粒整体平均温度的影响不大。
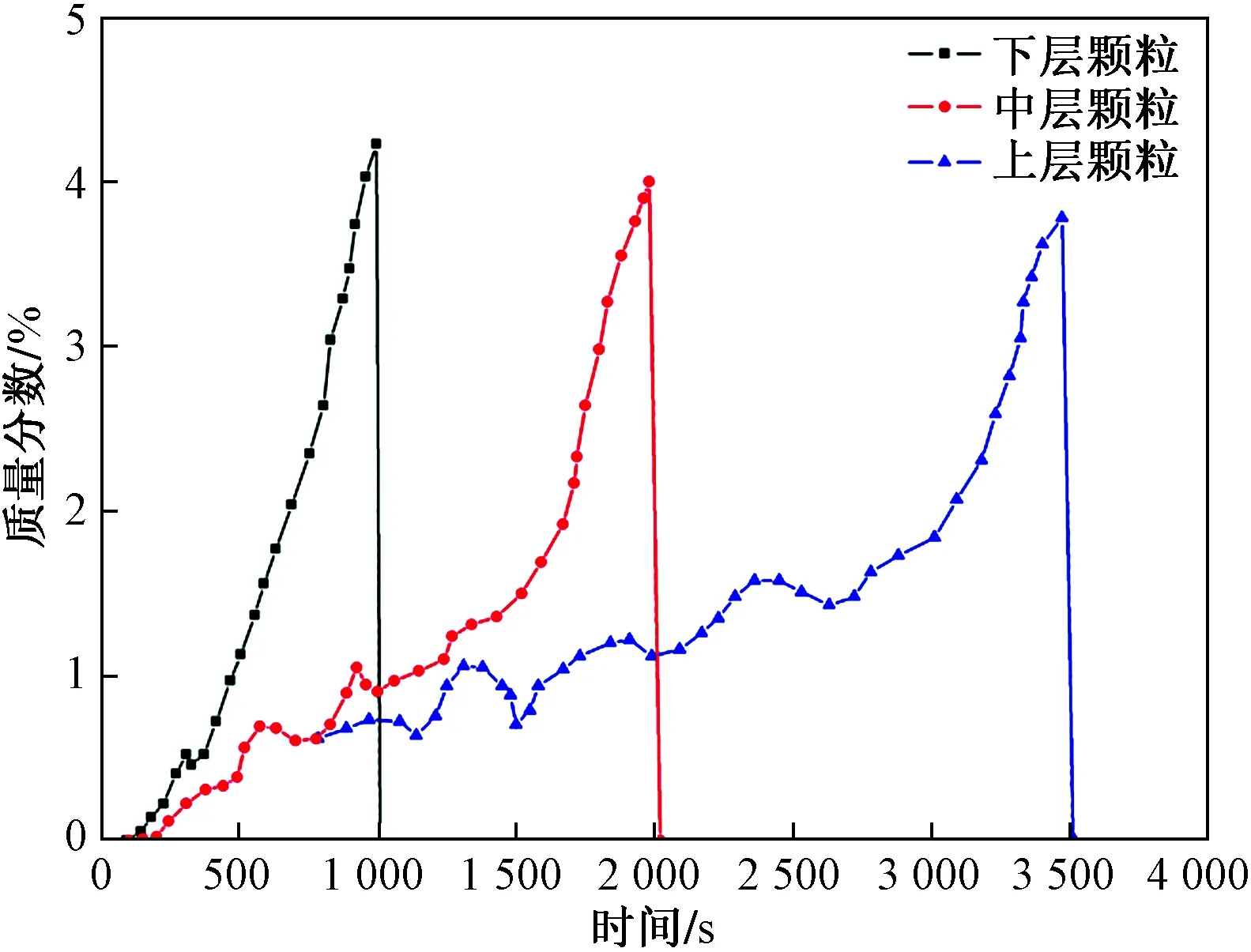
图11 颗粒中水蒸气质量分数Fig.11 Water vapor mass fraction in the pellet
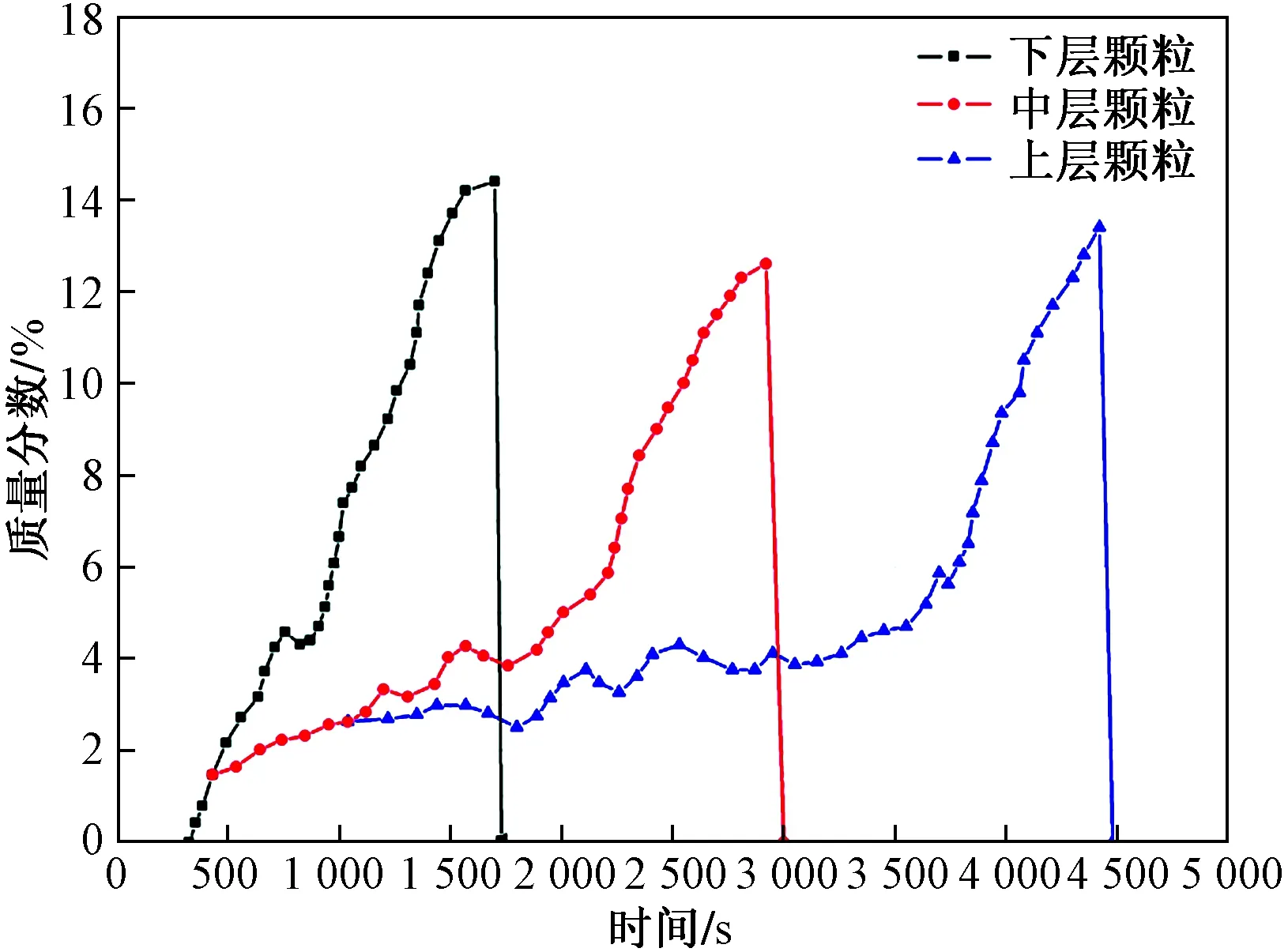
图12 颗粒中热解气体质量分数Fig.12 Pyrolysis gas mass fraction in the particle
图11所示为颗粒在不同高度下的蒸汽质量分数,图12所示为颗粒在不同高度下热解气体质量分数。由图11可知,如上所述,在100 s左右时,颗粒中的水分开始蒸发,并伴随着底部颗粒中的蒸汽质量分数的快速增加。对于较高位置的颗粒,也可以观察到蒸汽质量分数的适度增加,这些较高位置颗粒中蒸汽质量分数的增加主要来自底部颗粒的传质。
类似于图11,图12中所示为干酪根在热解初期,底部颗粒中的热解气体质量分数快速增加,由于热解反应所需的热量多和蒸汽传质过程的影响,故热解气体的传质过程较为缓慢。固定床内由于伴随着水分的蒸发、热解气体的析出以及入口处气体热载体向床层上部的输送,在同一时刻下,底部颗粒所处的周围气体中相比于上部具有较高的蒸汽含量和热解气体含量。因此,在固定床底部,颗粒和周围环境气体中蒸汽和热解气体浓度之间的梯度较小,这也是上部颗粒干馏进程较慢的另一个原因。
3.2 进气速度对干馏过程的影响
入口气体温度为600 ℃,油页岩颗粒半径为6.5 mm,固定床内油页岩颗粒堆积高度为2 400 mm。图13~图16分别给出了在不同进气速度下,固定床内不同高度处各层固体颗粒平均温度分布随时间变化的趋势,以及固定床整体平均温度随时间变化的规律。
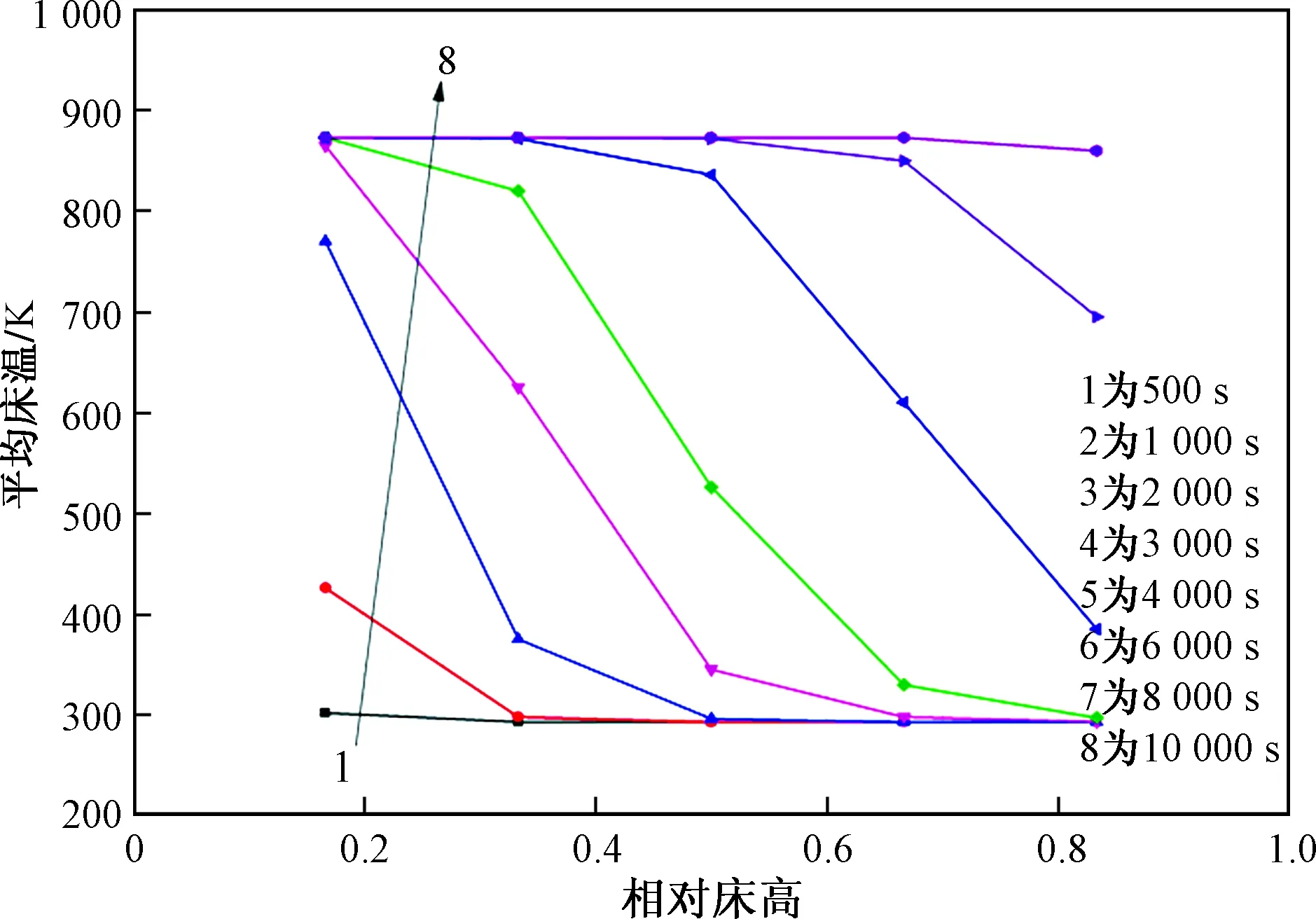
图13 流速为1.5 m/s时固定床内不同高度层颗粒的平均温度随时间变化情况Fig.13 The average temperature of particles at different heights in the fixed bed changes with time at a flow rate of 1.5 m/s
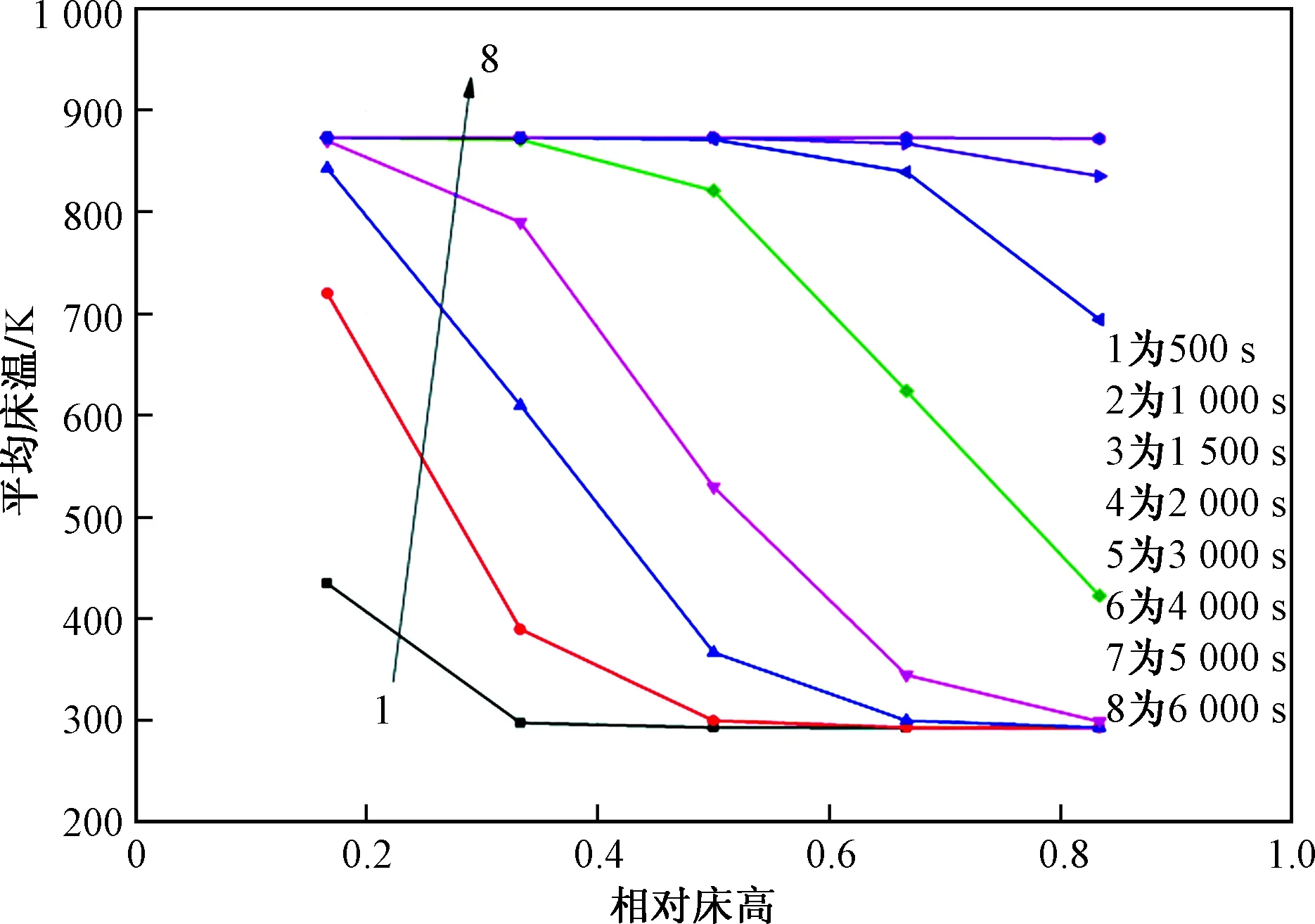
图14 流速为3 m/s时固定床内不同高度层颗粒的平均温度随时间变化情况Fig.14 The average temperature of particles at different heights in the fixed bed changes with time at a flow rate of 1.5 m/s

图15 流速为4.5 m/s时固定床内不同高度层颗粒的平均温度随时间变化情况Fig.15 The average temperature of particles at different heights in the fixed bed changes with time at a flow rate of 1.5 m/s
固定床内气固两相之间的换热方式主要以对流换热为主,对流换热系数在气体热载体向固体颗粒传递热量的过程中起重要的作用,因此围绕Nusselt数关联式[式(10)],通过改变入口流速来确定相应对流换热系数的值。图13~图15分别为入口流速为1.5 m/s(工况3)、3 m/s(工况1)以及4.5 m/s(工况2)时,固定床内不同高度层颗粒的平均温度随时间的变化情况。如图13~图15所示,改变进气速度对固定床内颗粒升温速度的影响较大。在0~1 000 s内,三种工况靠近进口处的颗粒温升较为明显,换热主要发生在靠近入口处的底层区域。在1 000~3 000 s内,工况1、2与工况3之间存在明显的温度差,而工况1和工况2之间的温差也逐渐增大,工况3由于对流换热系数小,因此沿固定床高度方向的热量传递缓慢,升温速度缓慢。在3 000~4 000 s内,工况2中颗粒整体平均温度达到气体热载体温度,此时固定床内的温度将逐渐保持稳定。工况1中颗粒整体平均温度虽然没达到进口气体温度,但温差不大,从图16中可以得到,在6 000 s之后,固定床内的温度达到稳定。工况3中沿床高方向的换热速度较慢,各层颗粒之间的温差较大,在靠近固定床出口处的顶层颗粒平均温度几乎没有变化。

图16 固定床内颗粒整体升温情况Fig.16 Overall temperature rise of particles in a fixed bed

图17 颗粒水分析出过程Fig.17 Particle water precipitation process
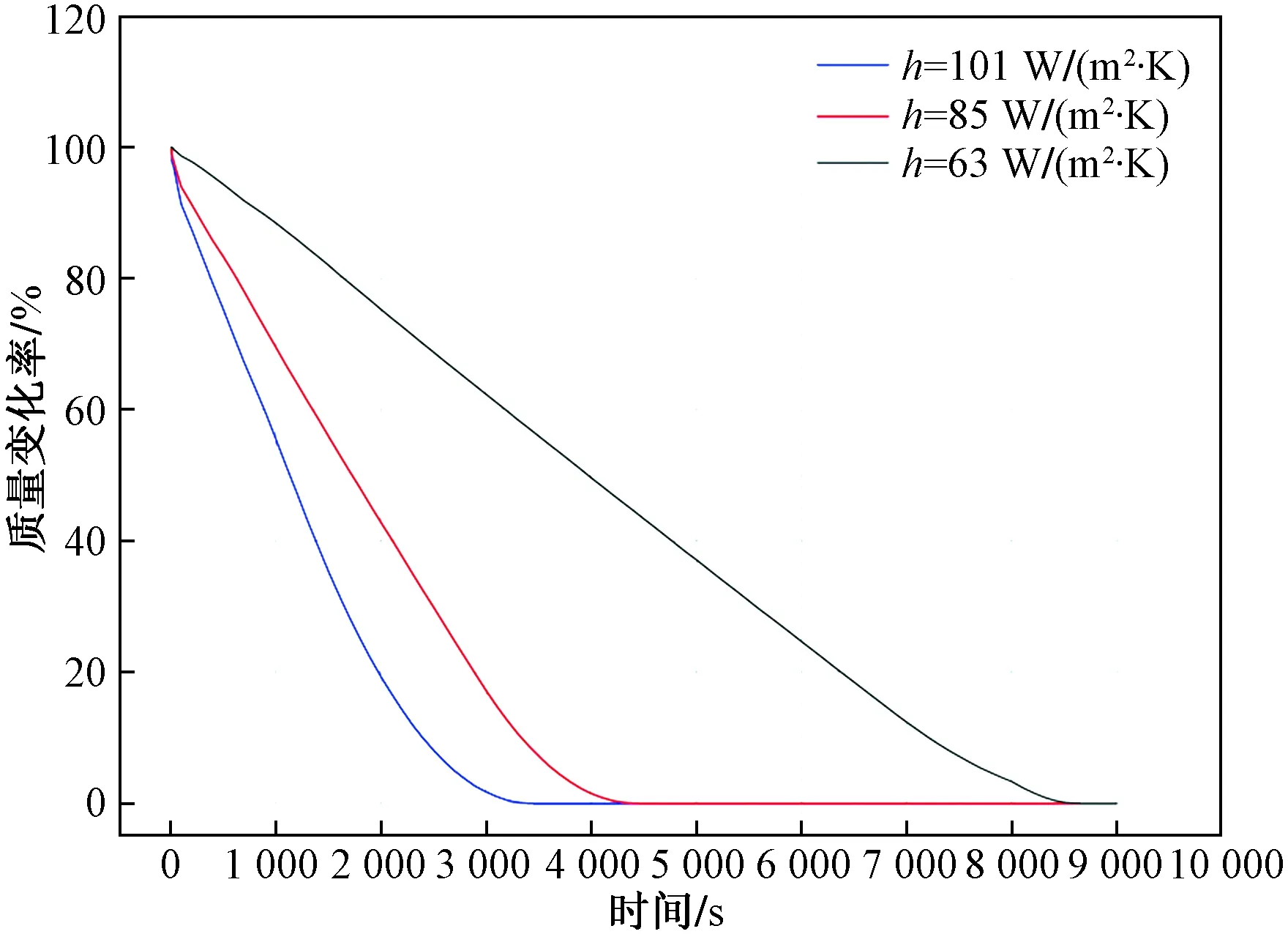
图18 颗粒热解气体析出过程Fig.18 Particle pyrolysis gas precipitation process
图17和图18分别为三种进气流速下,水分和热解气体析出过程随时间的分布规律,可以观察到,当提高进气速度时,相应的对流换热系数增大,反应进程明显加快。工况1在4 000 s左右时,颗粒中的水分全部析出,而在5 400 s左右热解气体全部析出,在大于6 000 s时,整体床温达到稳定状态。当入口流速提高0.5倍(工况2)时,在3 200 s左右时颗粒中的水分全部析出,而在3 800 s左右时颗粒中的热解气体全部析出,大于4 000 s时,整体床温达到稳定状态。当入口流速降低0.5倍(工况3)时,反应进程速度变化明显。此时,颗粒中的水分全部析出大约用时8 500 s左右,而颗粒中热解气体全部析出大约用时9 600 s左右,整体床温达到稳定状态时大约需要10 000 s,换热速度大幅降低,反应进程明显延后。
3.3 进气温度对干馏过程的影响
入口气体流速为3.0 m/s,油页岩颗粒半径为6.5 mm,固定床内油页岩颗粒堆积高度为2 400 mm。图19为进气温度对颗粒中水分蒸发速率的影响,可知,进气温度对油页岩中水分的最大蒸发速率和整体水分析出时间有显著的影响。在其他条件不变的情况下,进气温度分别为500、600、700 ℃时,水分的最大蒸发速率分别为1.25、1.66、1.85 g/s。进气温度提高100 ℃,干酪根热解前期水分最大蒸发速率提高约11.4%,进气温度降低100 ℃,干酪根热解前期水分最大蒸发速率降低约24.7%。由于进气温度越高,带入固定床反应区域内的热量越多,因此,随着进气温度的增加,水分全部析出所需要的时间减少,水分的最大蒸发速率增大。图20所示为不同进气温度下,颗粒中热解气体析出速率随时间的变化规律,可知,在其他条件不变的情况下,进气温度分别为500、600、 700 ℃时,颗粒中热解气体全部析出所需时间分别为6 500、5 400、4 700 s。进气温度的改变导致热解速率的明显变化,提高进气温度,热解气体全部析出的时间减少,加快热解进程
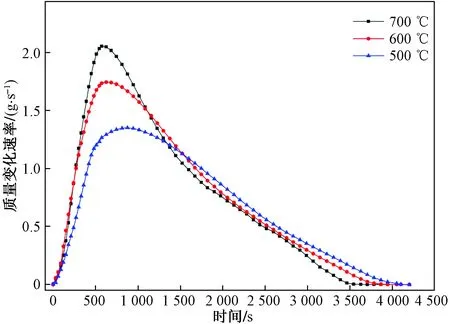
图19 进气温度对水分蒸发速率的影响Fig.19 Effect of intake air temperature on water evaporation rate

图20 进气温度对热解失重过程的影响Fig.20 Effect of intake air temperature on the process of pyrolysis weight loss
4 结论
通过建立详细的颗粒物料传热传质模型,对固定床内油页岩的干馏过程进行了模拟研究,并将实验结果与模拟结果进行对比验证,表明本文所用模型能够较好地预测固定床内温度、水分和挥发分随时间的变化规律。在本模型中,将固定床内的气体流动模拟为通过多孔介质的流动,其通过传热和传质的方式与固相之间进行相互作用。同时,分别从进气速度和进气温度等方面,对油页岩干馏过程进行详细研究。结果表明:当进气速度提高0.5倍时,干酪根热解反应进程加快1 600 s。当进气速度降低0.5倍时,干酪根热解反应进程延缓4 200 s,换热效率明显降低;进气温度提高100 ℃,干酪根热解反应进程加快600 s,热解过程前期水分最大蒸发速率提高约11.4%。当进气温度降低100 ℃时,干酪根热解反应进程延缓1 300 s,热解过程前期水分最大蒸发速率降低约24.7%;固定床内由于伴随着水分的蒸发、热解气体的析出以及入口处气体热载体向床层上部的输送,在同一时刻下,底部颗粒所处的周围气体中相比于上部具有较高的蒸汽含量和热解气体含量。底部颗粒和周围环境气体中蒸汽和热解气体之间的浓度梯度相比于上部颗粒较小,这也是固定床内上部颗粒干馏进程较慢的一个重要原因。

