基于动态规划和黄金分割法的环状天然气管网运行优化

杨 毅 刁洪涛 向 敏 孙晓波 柳建军

1.中国石油北京油气调控中心 2.中石油管道有限责任公司 3.中国石油管道科技研究中心

0 引言

随着中国石油天然气管道业务的飞速发展，截至2015年，中国天然气管网主干管道里程已经达到了6.3×104km，发展成为了一种环套环的复杂管网[1-2]。与此同时，各压气站的燃驱压缩机机组的数量也在逐渐增加。据统计，截至2019年管网中燃驱压缩机机组比例超过了60%。经研究，这种含有燃驱的大型复杂天然气管网耗气量通常占干线总输量的2%～5%[3]，如果通过优化运行技术，耗能每降低1%，每年将节约3千万元的能耗费用。

天然气管网运行优化技术已经发展多年，单条管道的稳态优化数学模型和求解技术十分成熟，管网稳态运行优化数学模型也基本成熟，但是，由于管网稳态优化数学模型的求解难度较大，管网模型的求解，特别是大型天然气管网稳态运行优化模型求解，还需要进一步完善或研发[4-10]。1998年，Carter[11]提出了一种研究方法，把大管网分割成多种特殊的小结构，再利用非序列动态规划算法分别求解每个小结构的优化组合，最后组合成该管网的最优解。该方法的缺陷是没有考虑管网内部流量分配和压缩机耗气量对于优化结果影响。随后，各国学者对此方法进行了改进，Rios-Mercado等[12-15]在进行小结构划分的基础上，分两步进行优化计算，优化了求解步骤，但是未考虑燃驱耗气量对管道流量的影响。

在复杂管网稳态运行优化模型中综合考虑管网内部流量分配和燃气机组耗气量对管网流量的影响，并对其进行求解，能有效攻克复杂管网优化技术难题，可以为当前中国大型天然气管网稳态运行优化提供参考。

1 单线管道与环状管网运行优化数学模型的对比

1.1 单线管道运行优化数学模型

单线管道通常为一条含有多个压缩机组压气站和分输站的管道（图1）。通常已知管道首段（CS1）压气站的进站压力、流量（QS）、温度，以及各个分输站（含压气站）的分输量（Q）。在已知CS1出站压力的情况下，可根据压缩机组的特性计算得到燃驱的耗气量（g1），进而可得到出站流量（管道流量，q1）。

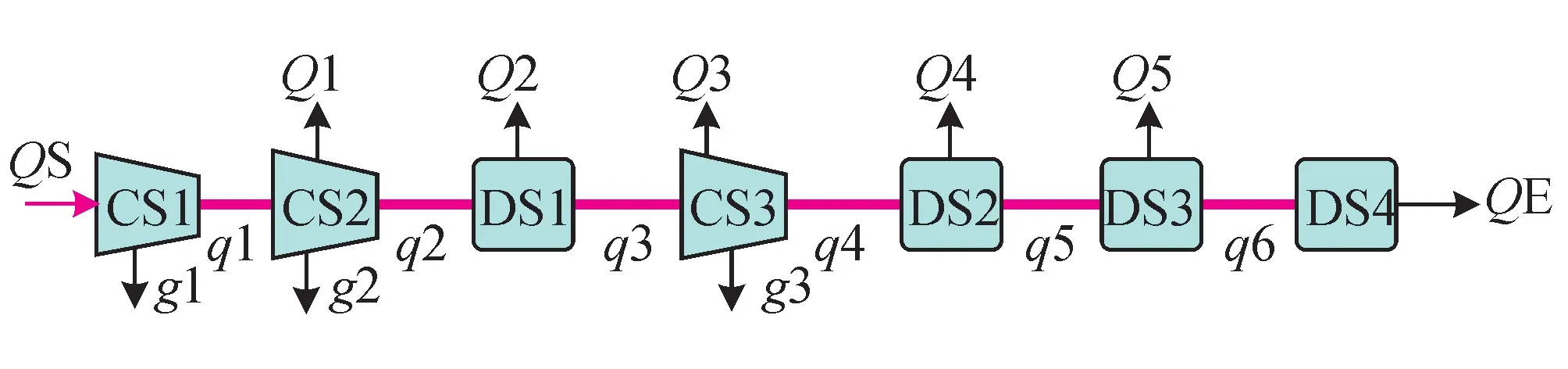
图1 单线天然气管道示意图

1.1.1 目标函数

单线管道运行优化通常以全线总能耗（F）最小作为优化目标，其优化数学模型如下[9,16-21]：

式中c表示压缩机站总数；Ni表示第i站压缩机组总功率，kW。

1.1.2 约束条件

管道运行需要满足一定的管道承压能力不等式约束、水力热力等式约束、压缩机组的性能约束以及节点流量平衡约束等。单线管道运行优化数学模型约束条件如下[9,16-21]：

式中kij表示压缩机开关变量；c表示压缩机站总数；Ni表示第i站压缩机组总功率，kW；Dij表示第i站第j台压缩机的可行域；yij表示第i站第j台压缩机的过流量，m3/s；Yi表示第i站的过流量，m3/s；ps,i、pd,i表示第i站的进、出站压力，如果是分输站则两者数值相同，MPa；Ts,i、Td,i表示第i站的进、出口温度，如果是分输站则两者数值相同，K；pd,imax、ps,imin表示第i站的最高出站压力和最低进站压力，MPa；Td,imax表示第i站的最高出站温度，K；m表示站场总数；n表示站内机组总数；cg表示燃驱站总数；mp表示管道的总数；gi表示第i站总耗气量，m3/s；qi表示第i条管道的输量，m3/s；Qi表示第i站的分输量，m3/s；fp()、fc()、fg()、fn()分别表示管道方程、压缩机功率方程、燃料气量方程及节点流量平衡方程。

式（2）中fn()为节点流量平衡方程，考虑了燃驱机组耗气量因素对于压气站下游管道流量的影响，改进了前人的优化数学模型，也进一步提高了优化模型与实际情况的符合度。

1.1.3 优化变量

对于单线输气管道，优化数学模型的优化变量仅有一种，即压缩机站的出站压力（pd,i）：

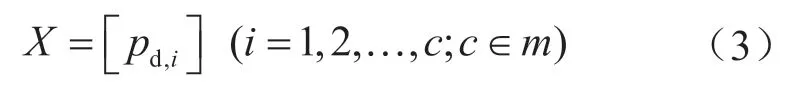
1.2 含环状结构的枝状天然气管网运行优化数学模型

含环状结构的枝状天然气管网通常会含有多个环及多个分枝管道，并含有多个压气站和分输站（图2）。CS1压气站、CS2压气站、DS1分输站、CS3压气站和CS4压气站及其相连的管道形成了一个上下半环都含压缩机站的环状管网，CS5压气站和DS5分输站组成了第3个环，DS8至DS14分输站及其相连管道组成了一个枝状管网。

图2 含环状结构的枝状天然气管网示意图

含环状结构的枝状天然气管网运行优化数学模型的目标函数是管网系统压缩机组总功率，见式（1）。需要满足的约束条件有管道承压能力不等式约束、水力热力等式约束、压缩机组的性能约束以及节点流量平衡约束等。因此，含环状结构的枝状天然气管网运行优化数学模型的约束条件与式（2）描述内容相同。由于考虑了燃驱机组耗气量对于压气站下游管道流量的影响，其系统的总进气量高于各个分输站流量之和，改进了前人的管网运行优化数学模型，更加符合天然气管网的实际运行情况。

然而，含环状结构的枝状天然气管网运行优化数学模型的决策变量与单线管道的优化数学模型有不同之处。上半环第一条管道不同的流量（q1）数值，将产生不同的g2（CS2站耗气量）数值，q1成为影响优化效果的一个决策变量。因此，含环状结构的枝状天然气管网运行优化数学模型的优化变量有两种，如式（4）所示：

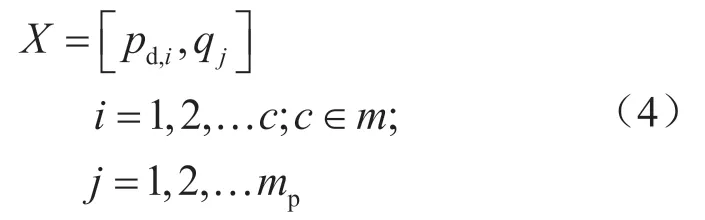
1.3 数学模型分析

上述改进后的单线管道和含环状结构的枝状天然气管网稳态运行优化数学模型的基本特点是：优化模型含有等式约束、不等式约束和整数约束，约束条件中存在线性约束和高度非线性约束。由约束条件组成的优化模型的可行域为非凸集[8-9]。因此，改进后的两种优化数学模型都具有较高的求解难度。

2 动态规划和黄金分割算法

2.1 动态规划算法

利用动态规划算法求解上述模型的一般含有以下4个主要部分组成：“确定状态空间”“站间递推”“站内递推”和“算法回溯”[18,20,22]。

2.1.1 状态空间的确定

在动态规划算法中，某压气站所有的可行出站压力的集合即为状态空间。状态空间的上界可取管道的设计压力。

2.1.2 站间递推

站间递推是由某压气站的出站工况得到下一压气站的进站工况的计算，以站间管段的水力、热力计算为主。

2.1.3 站内递推

站内递推的目的是由压气站的进站工况得到出站工况，并计算得出相应的压缩机开机台数、转速和功率以及耗电量或耗气量等参数，其中该方案下的站总功率是重要的对比参数。

2.1.4 算法回溯

对第n个阶段的站间和站内递推完成以后，便在末站得到若干个进站工况对应的若干个全线总能耗。此时需要对整个方案进行回溯。回溯即根据最优方案所记录的各压气站的进、出站工况，确定管道最优运行方案。

对于单线管道，上述算法能够快速有效地求解出最优解[5,14,16]。但是由于环状天然气管网运行优化数学模型优化变量中含有了管道流量（qj），qj未知时第（2）部分“站间递推”无法进行，动态规划算法失效。因此，Carter[11]和Rios-Mercado 等[12]通过采用“分割”模型和预算管网内qj的思路，只有在不考虑自耗气量的情况下，才能够计算出相对优化的结果。

2.2 黄金分割算法

该算法是用于对一元函数f(x)在给定的初始区间[a, b]内搜索极小点的一种方法，是一种经典算法。该算法的具体步骤可以简化如下：在区间[a, b]内取两点，a1和a2把[a, b]分为3段[22]：

2.3 动态规划和黄金分割混合算法

按照Carter[11]对于管网模型分割的思路，对于如图2环状管网，每一个环状或枝状都可以看作一个小分割结构，则图2管网可以划分为5个结构（4个环状和1个枝状）。而对于每个结构来说，在已知当前结构出口压力、流量、温度和下一结构入口压力的情况下，如能确定上、下环首端的q1或q2，则可以利用动态规划算法中的“站间递推”思路，获得其他关键参数。通过试算分析，可以采用黄金分割算法提前获得q1或q2数值，进而再采用动态规划算法进行后续计算。

基于上述分析，结合管网模型分割思路，将黄金分割算法与动态规划算法进行融合，形成了改进后的动态规划和黄金分割混合算法，求解步骤如下。

1）状态空间的确定：如动态规划算法中的“状态空间的确定”。

2）结构间递推：以环作为递推的对象，考虑机组耗气量对管道内流量的影响。

3）结构内递推：如果环状结构上、下环均为含有压气站的单线管道，则可以采用动态规划算法中的“站间递推”相关算法，如果结构上、下环内不含压气站或者结构为单管或枝状管道，则可采用天然气管网稳态仿真技术计算出各个站的相关参数[8]。

4）站内递推：如动态规划算法中的“站内递推”。

5）算法回溯：如动态规划算法中的“算法回溯”。

由于该求解技术既分别考虑了管网中环状结构和枝状结构对于管道流量分配的影响，也充分考虑了燃驱机组耗气量对管道内流量的影响，因此可以有效应用和解决具有环状结构和枝状结构管网的稳态运行优化问题。

3 案例分析

图2为华北地区某现役天然气管网结构图，其中第1个结构为环状结构，上、下环管道都有压缩机站，第2和第4个环的上半环都有分输站，第5个结构是含3个分支的枝状结构。该管网含5个压缩机站和14个分输站。其中：CS1站含6台燃驱压缩机，CS2站含2台电驱压缩机，CS3站含2台燃驱压缩机，CS4站含5台电驱压缩机，CS5站含5台电驱压缩机。该管网设计压力为10 MPa，管径为1 016 mm，管网全长为1 800 km。

由于该管网第1个环状结构上、下管道都具有压缩机站，因此上、下环管道的流量成了一个决策变量，常规的动态规划算法已经无法求解出有效结果。该管网日常运行比较注重耗能率。因此，以能耗最低（功率最小）作为稳态运行优化的目标。

基于上述动态规划和黄金分割混合算法的求解思路和方法，通过采用VC++6.0编制应用程序，分别计算获得了该管网夏季和冬季某日的最优运行方案，在普通台式机上求解模拟计算时间约2 min。夏冬季优化结果的关键参数以及与实际运行方案的对比数据，分别见表1和表2所示。

从表1的对比结果可以看出，优化后的总功率较优化前运行工况的总功率降低了6%，优化效果比较明显。从具体的数据可以看出，功率减少量来自CS3和CS4两个压缩机站，通过查看两个站内压缩机的运行点，发现优化前工况中CS3站内压缩机已经接近喘振线，效率比较低。而通过降低压比，降低了能头，提高了该站机组的运行效率，进而减少了功率消耗。CS4站也是同样情况，减低了压比，提高了效率，减少了功率消耗。

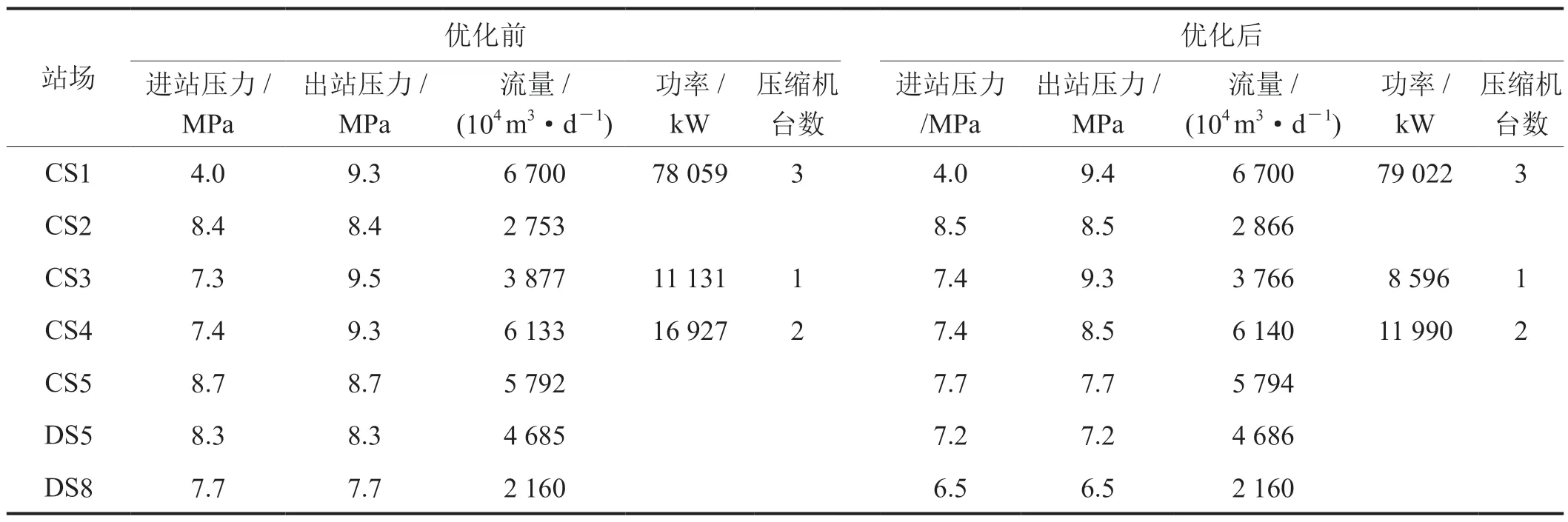
表1 夏季某日优化前、后运行工况的对比数据表

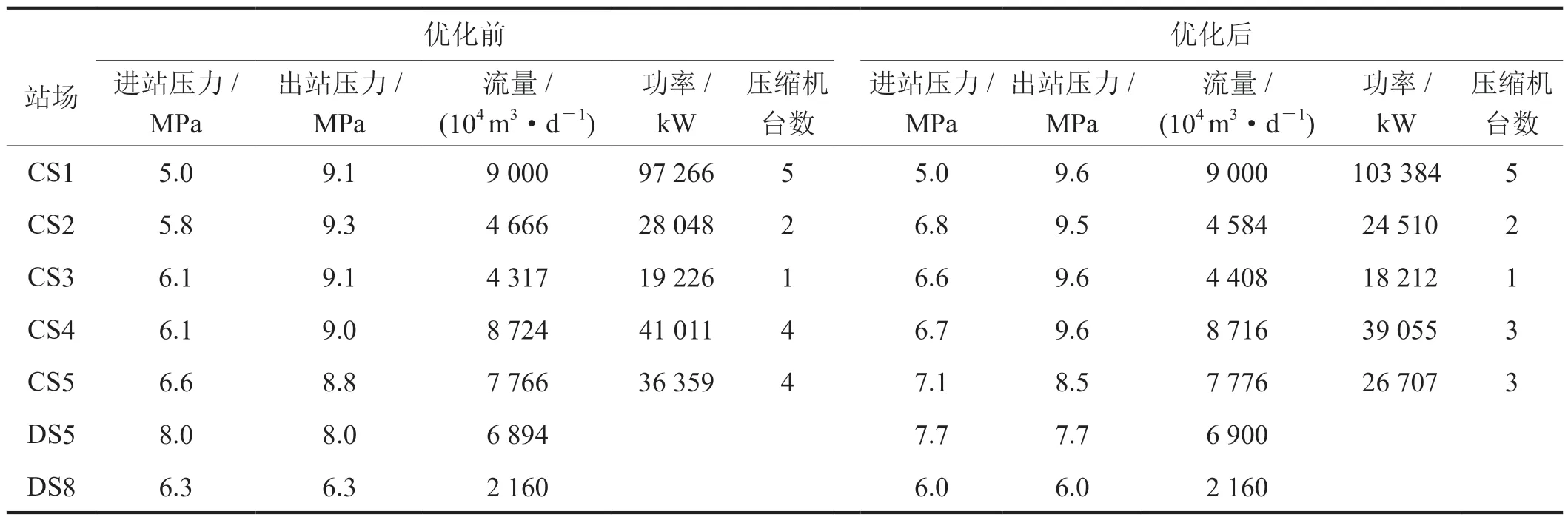
表2 冬季某日优化前、后运行工况的对比数据表

从表2的对比结果可以看出，优化后的总功率较优化前运行工况的总功率降低了4%，优化效果非常明显。

优化后的运行方案通过增加前面3个压气站的出站压力，优化了后面2个压气站的开机台数，总开机台数减少了2台。同时，增加了管网的管存量，为应急提供了较高的管存资源。从具体的数据可以看出，功率减少量主要来自CS2和CS5两个压缩机站，通过降低了两站的进、出站压比，提高了两个压缩机站的运行效率。

4 结论

1）由于当前中国天然气管网可以分割为多个含环状结构的枝状管网和不含环状结构的枝状管道，因此，研究含环状结构的小型枝状管网的稳态优化问题具有一定的实际应用价值，也可为解决大型天然气管网稳态运行优化问题提供参考。

2）单线管道运行优化数学模型和管网运行优化数学模型中的节点流量平衡方程中考虑燃驱耗气量，更能够反映管网的真实运行情况。

3）管网的运行优化数学模型与单线管道的运行优化数学模型的主要区别在于优化变量中增加了管道流量。因此常规的动态规划算法无法求解管网运行优化数学模型。

4）在对含环状结构的枝状管网进行结构划分的基础上，结合动态规划和黄金分割的混合算法能够有效解决含环状结构的枝状管网的稳态运行优化问题。

5）对于某华北地区还含环状结构的枝状管网而言，提高压缩机站的出口压力能够有效降低系统的功率消耗，而且增加了管网的管存量，提供了额外的应急资源。