基于边界元法的高精度交流机械臂伺服动力特性分析

蓝雄

柳州职业技术学院 机电工程学院，广西 柳州 545006

随着近年来科技的高速发展，越来越多的科技产品广泛应用于人类生活与生产中，机械臂就是随之诞生的高科技产物[1]。机械臂可应用于工业生产、航天产品以及农业种植等众多具有高精度要求的行业中，其因高精度和智能化等优势有效提升生产以及产品精度[2]。在目前高速发展的社会情形下，传统机械臂已渐渐无法符合越来越高的未来发展需求，设计具有高精度高伺服性能的机械臂具有重要意义[3]。

目前对复杂机械的动力特性研究较多，但是针对高精度交流机械臂伺服动力特性研究相对缺乏，因机电耦合问题极易造成机械臂控制精度低，可靠性差，运行稳定性较差等问题[4]。研究基于边界元法的高精度交流机械臂伺服动力特性，建立具有高精度高伺服性能的交流六自由度柔性机械臂模型，基于边界元法对该模型的动力特性有效分析，对于机械臂的伺服性能以及机械臂的高精度运行提供理论依据。

1 高精度交流机械臂伺服动力特性分析

1.1 机械臂伺服传动系统

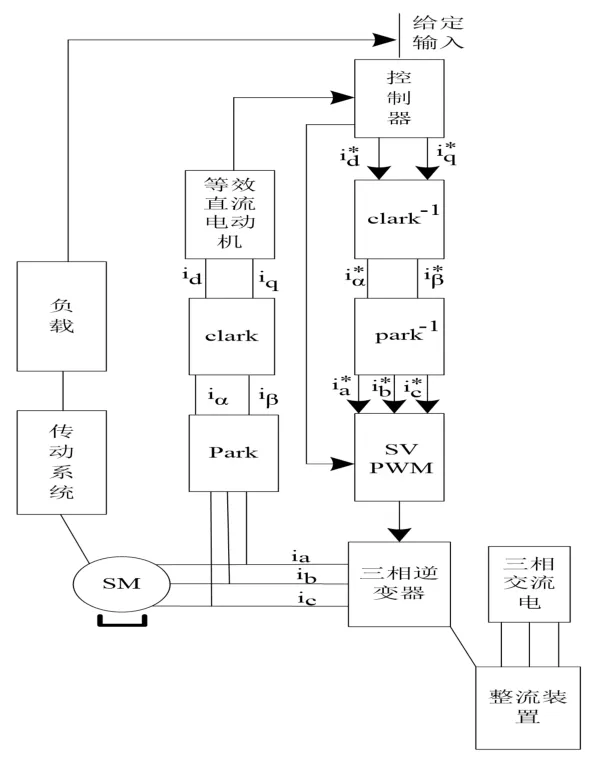
图1 矢量控制子系统原理图Fig.1 Principle of the vector control subsystem

柔性机械臂中应用的永磁同步电动机具有时变、强耦合以及非线性多变量特性[5]，选取转子磁链定向矢量控制子系统应用于机械臂伺服传动系统中，伺服控制系统原理如图1 所示。

图1 为针对6 轴关节机械臂设计的机械臂伺服传动系统中的矢量控制子系统，选取齿轮传动系统控制机械臂传动，分别选取RV 减速机与谐波减速机控制机械臂的1、2、3 关节与4、5、6 关节，因齿轮传动机构较大[6]，利用质量-弹簧-阻尼器建立传动系统。传动系统输入和输出分别为电动机驱动力矩Ti驱动轴转角θi以及机械臂关节运动角度θL与关节力矩TL，力的平衡微分方程可通过输入轴与输出轴获取[7]，力的平衡微分方程如下：

以上公式中：Bi与Bo分别表示电动机轴系的粘滞阻尼系数以及机械臂轴系的粘滞阻尼系数；Ji与Jo分别表示驱动轴系的等效惯量以及负载轴系的等效惯量；T表示作用于齿轮副上的等效转矩以及；i表示齿轮以及齿轮速比。

利用公式（1）和公式（2）获取输入与输出角度关系公式如下：

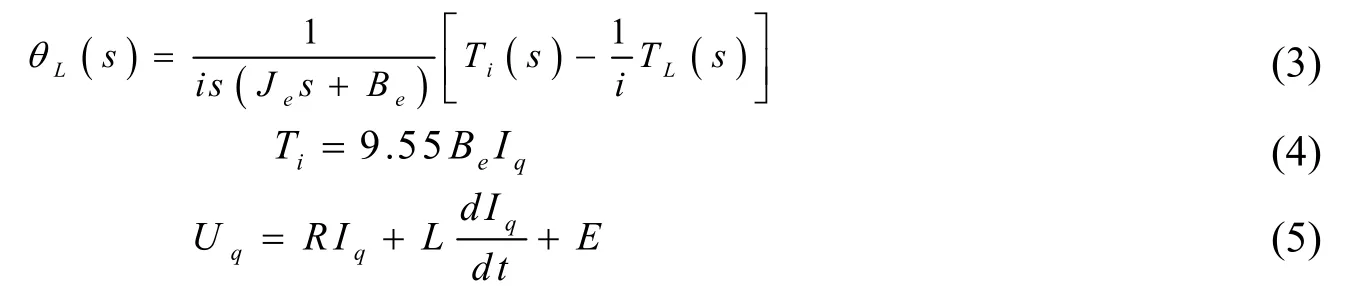
其中，Be表示等效阻尼系数，Je表示折算至负载端的总转动惯量。

选择三环控制子系统控制机械臂的稳定运行，并有效提升机械臂的运行精度[8]，三环控制子系统中最外环为位置环，中间环为速度换，最内环为电流环，依据公式（4）（5）（6）获取机械臂关节的伺服控制系统，机械臂关节的伺服控制系统中电流环传递函数如下：

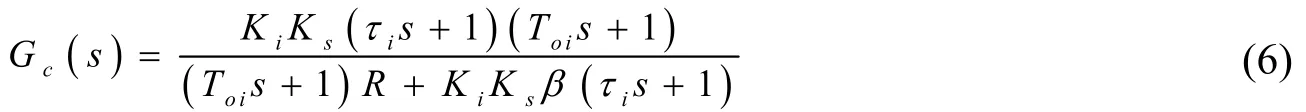
机械臂关节的伺服控制系统中转速环传递函数如下：

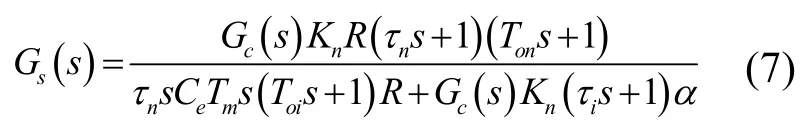
机械臂关节的伺服控制系统中位置环传递函数如下：

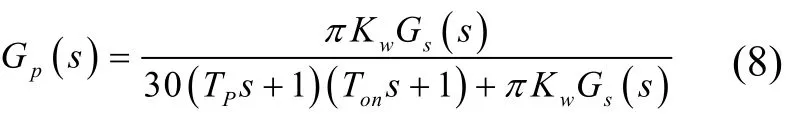
三环控制子系统的传递函数用位置环的传递函数表示，以上公式中，Ks表示PWM 变换器的放大系数；Ts表示PWM 变换器的延迟时间；Toi表示电流调节器的滤波时间常数；Ton表示转速调节器的滤波时间常数；α表示电流环的反馈系数；β表示转速环的反馈系数；Cm表示即刻励磁下电动机转矩系数，Tm表示电力拖动系统机电时间常数，其中Tm=GD2R/375CeCm。

1.2 高精度交流机械臂伺服边界元法动力特性分析

图2 梁元件合成图Fig.2 Composite view of beam components

上文建立了机械臂伺服传动系统，选取边界元法分析利用机械臂伺服传动系统控制的6 自由度柔性机械臂动力特性[9]，依据获取的动力学方程检测机械臂的高精度交流伺服性能。

机械臂中包括若干元件，由不同元件结合连接组成机械臂。选取边界元法建立机械臂中各元件的边界方程[10]，选取由两个梁元件合成的机械臂中一部分介绍机械臂整体的边界元建模解析过程[11]。机械臂中梁元件合成图如图2 所示。

针对图2 通过机械臂的梁元件的单元边界方程获取整体机械臂的动力特性分析。机械臂中的梁元件各端均具有自由度方向为6°，梁元件中其中一个方向的长度与另两个方向长度相比差别较大[12]，机械臂受到激振力会形成弯曲、扭转与纵向的联合震动[13]。选取机械臂中梁元件的弯曲震动的动态基本解获取机械臂中梁单元边界控制方程如下：

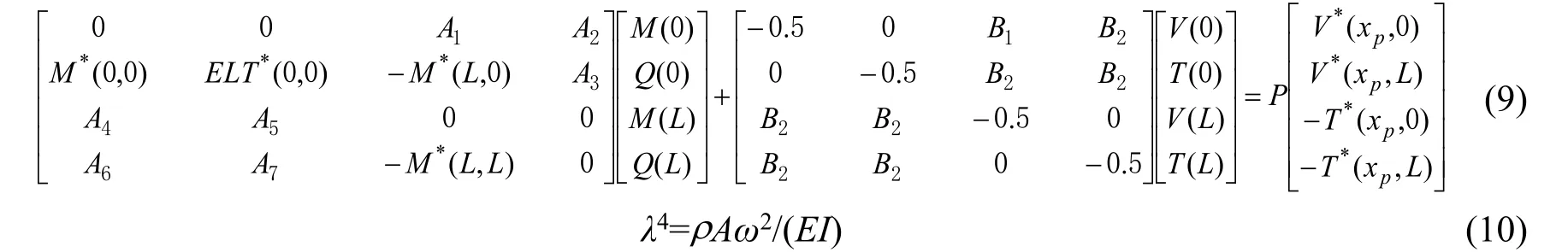
以上公式中，V表示机械臂梁元件弯曲震动时挠度；T表示机械臂梁元件弯曲震动时挠角；M表示机械臂梁元件弯曲震动时弯矩；Q表示机械臂梁元件弯曲震动时剪力；V*表示机械臂梁元件弯曲震动时挠度的动态基本解函数；T*表示机械臂梁元件弯曲震动时挠角动态基本解函数；M*表示机械臂梁元件弯曲震动时弯矩动态基本解函数；Q*表示机械臂梁元件弯曲震动时剪力动态基本解函数；L与xp分别表示梁元件的长度与激振力P作用点坐标；ρ表示材料密度；A表示材料面积；ω表示材料频率；E表示材料弹性模量；I表示材料的惯性矩。

公式（9）中矩阵内各元素分别为：

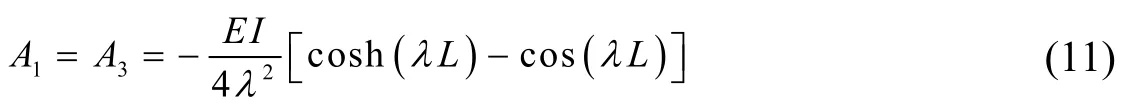
通过以上过程可获取机械臂梁单元于纵向和扭转方向的边界方程[14]，将不同方向的边界方程组合依据机械臂中梁元件各方向的震动特点获取机械臂中梁元件的动力学方程如下：

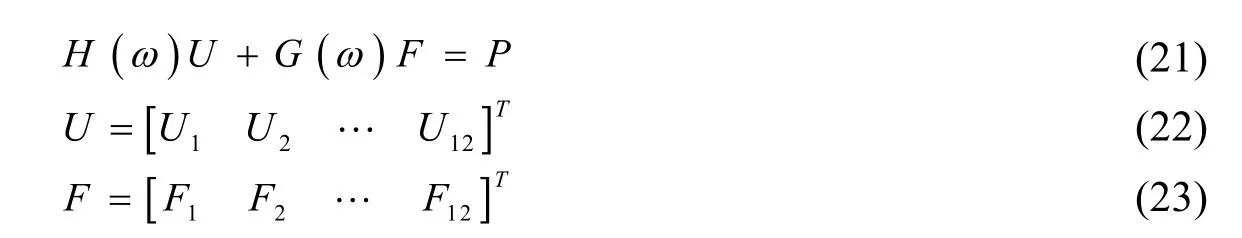
以上公式中，H与U均表示位移，G与F分别表示力系数阵与力列阵。

变换、整理公式（21）后，可获取图1 中机械臂中两个梁元件的动力学方程如下：

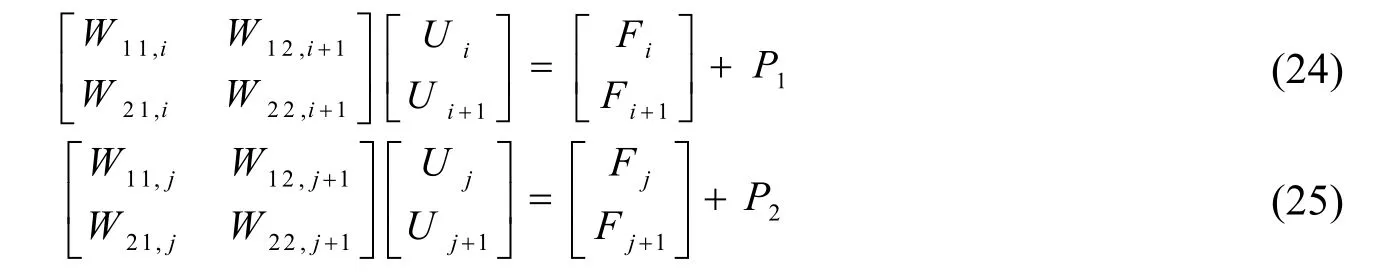
以上公式中，W表示完成变换的系数矩阵。

建立相应的边界结合关系式与机械臂的结合边界中，依据作用力与反作用力条件可得图1 中a处边界上力的约束关系公式如下：

公式（26）中，S表示坐标变换矩阵。

设Ka与Ca分别为a处结合部的刚度阵与阻尼阵，可得如下关系式：

在a处Fi+1、Fj力与位移约束关系可利用图1 中a处两端力坐标系变换关系获取，公式如下：

依据公式（26）、公式（28）和公式（29）将公式（24）、（25）结合获取机械臂中两个梁元件合成方程式如下：

公式（30）中，表示复刚度阵，=Ka+iωCa；P表示与P1、P2关联的列阵。

依据以上两个梁的步骤依次合成，获取由多个元件组成的机械臂整体结构，可知机械臂的动力学方程如下：

通过公式（31）即可获取机械臂结构的固有频率特性，同时可获取机械臂结构各阶频率所对应的阵型[15]，依据固有频率特性和各阶频率分析由机械臂伺服传动系统控制的高精度交流机械臂伺服动力特性。

2 实验分析

采用本文方法建立机械臂伺服传动系统，并将该系统应用于六自由度柔性机械臂中，获取的实验装置图如图3 所示，并采用本文方法分析机械臂的动力特性。

图3 六自由度机械臂实验装置图Fig.3 Six-degree-of-freedom mechanical arm experimental device diagram

设置六自由度柔性机械臂实验装置负载重量与重力加速度分别为1.0 kg 以及10.0 m/s2。柔性机械臂参数见表1。

表1 机械臂参数Table 1 Mechanical arm parameters

通过本文方法将柔性机械臂关节速度转换至电机速度，跟踪机械臂在空载、150 Nm 负载、300 Nm负载情况下的运行情况，速度跟踪结果如图4 所示。

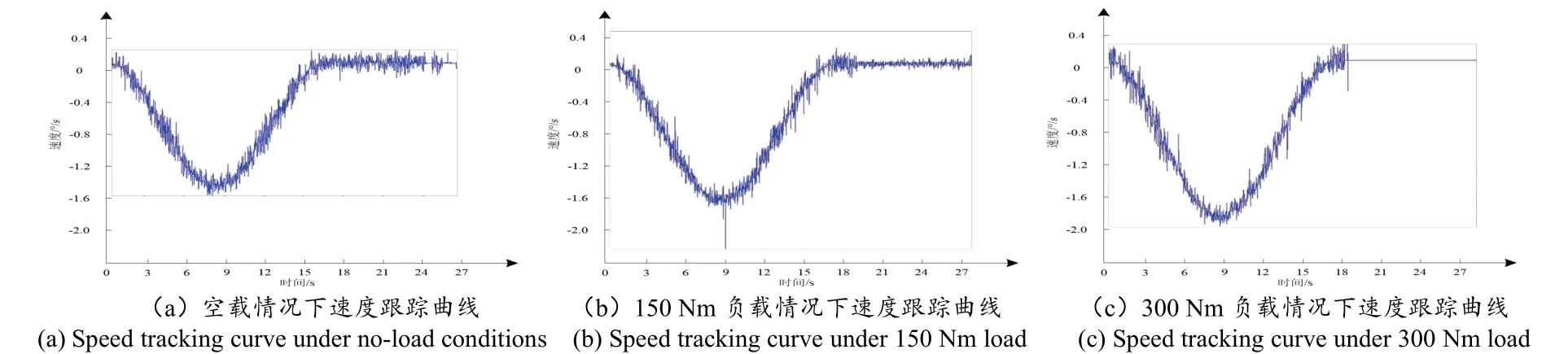
图4 机械臂速度跟踪结果Fig.4 Robot arm speed tracking results

分析图4 柔性机械臂在不同负载情况下的速度跟踪结果可知，机械臂的关节电机可跟踪电机输入速度效果较好，且负载大小与速度波动呈反比，负载越大情况下，速度波动越小，验证了本文方法的伺服性能。

不同负载情况下柔性机械臂的关节位置估计跟踪结果如图5 所示。

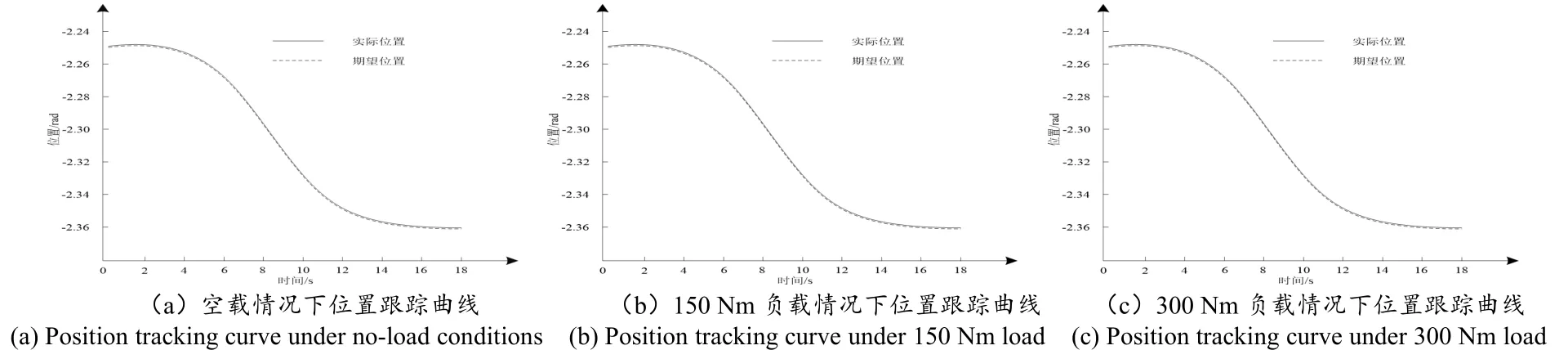
图5 机械臂位置跟踪结果Fig.5 Robot arm position tracking results

通过图5 实验结果可以看出，该机械臂的关节实际位置与期望位置基本吻合，验证了本文机械臂的跟踪高精度，说明本文机械臂响应关节期望位置速度较快；在实验中机械臂关节结束运动时位置波动极小，波动范围与稳态误差小于18"以及1.5´，并且机械臂在负载变大情况下，仍保持快速的影响速度，波动范围以及稳态误差没有收到影响，再次验证了机械臂的高精度以及伺服稳定特性。

采用本文方法获取实验装置六自由度柔性机械臂的动力学方程，通过动力学方程建立六自由度机械臂合成单元的数据文件，获取前6 阶固有频率结果如表2 所示。

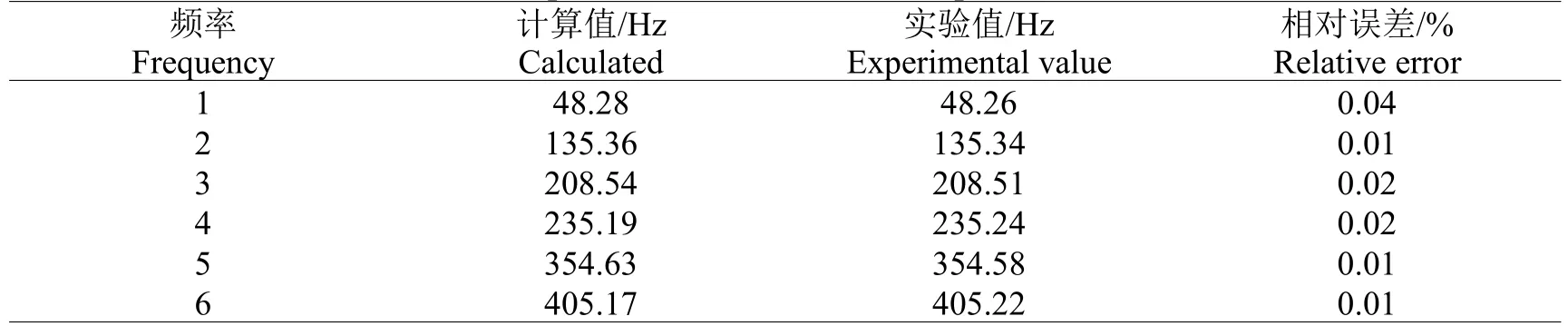
表2 计算值与实验值对比Table 2 Comparison of calculated and experimental values

通过表2 实验结果可以看出，采用本文方法分析高精度交流机械臂伺服动力特性结果较为精准，相对误差均在0.05%以内，验证了本文方法分析高精度交流机械臂伺服动力特性的准确性。

3 结论

机械臂是目前广泛应用于各种行业的高科技产物。选取转子磁链定向矢量控制系统应用于机械臂伺服传动系统，并将三环控制系统应用于机械臂伺服传动系统中，有效提升高精度交流机械臂伺服特性，并利用边界元法建立高精度交流机械臂动力学方程，通过动力学方程有效分析机械臂的动力特性。实验结果表明，通过该方法获取的机械臂伺服传动系统应用于六自由度柔性机械臂中，具有较好的高精度伺服特性，且通过固有频率结果验证了该方法的动力特性分析结果。