连续梁桥支座更换顶升方案的优化方法

(1.湖南省交通规划勘察设计院有限公司， 湖南 长沙 410008；2.中国电建集团 贵阳勘测设计研究院有限公司， 贵州 贵阳 550081)

0 引言

桥梁支座作为桥梁上、下部结构的传力构件，是桥梁结构的重要组成部分，在桥梁正常使用过程中，当支座因产生病害而无法正常传递上部结构荷载时，需要对其进行更换，以保证桥梁结构的安全[1]。相较于桥梁整体结构，支座的设计使用寿命较短，早期建设的桥梁已然进入支座更换爆发期，为了保证支座更换过程中结构的安全性及施工的高效性，有必要对支座更换方案进行研究和优化设计。

支座更换施工时，需要将上部梁体顶升以提供操作空间，根据顶升方式不同，目前支座顶升更换方案主要有“整联同步顶升”和“横桥向同步，纵桥向逐墩或多墩顶升”两大类[2-6]。“整联同步顶升”方法是先解除上部构造联间约束，通过在整联各支点位置附近布置千斤顶，采用同步顶升系统控制，实现整联上部结构整体顶升，因此不会引起上部结构内力变化。该方法的优点是：上部结构只发生刚体移动，不会在梁体内产生次内力；该方法的缺点是:需要数量庞大的千斤顶，施工造价高，该缺点在装配式桥梁支座更换时尤为突出，由于采用了大量的千斤顶，实际顶升中，难以保证各千斤顶绝对同步，这将改变上部结构的受力状态，甚至导致梁体开裂。

陈露晔等[6]首先提出采用“纵向单点(逐墩)，横向同步”法更换支座，该方法是通过横桥向布置单排千斤顶，同步控制横向顶升量，顶升完毕将支座更换后落梁，将千斤顶纵桥向移至下一位置顶升，以此类推，完成全部支座更换。该方法仅需少量人员、千斤顶及临时支架，工程造价低，由于同步点较少，可更加有效地避免顶升不同步造成的风险，该方法对连续梁桥的支座更换有较明显的优势。

“横桥向同步，纵桥向逐墩或多墩顶升”法的核心问题是顶升方案的确定，在分阶段顶升过程中，最期望的状态是仅通过单点顶升完成本支点支座更换，单点顶升时相当于梁体在顶升点受到一定的强迫位移，梁体将产生附加内力，当顶升量过大时，可能引起局部截面开裂，甚至破坏，因此单点顶升时，每个支点都有一个极限顶升量。当某支点更换支座所需顶升量超过极限顶升量时，需要在附近桥墩进行辅助顶升，以改善梁的受力。因此，该方法的难点在于如何选取辅助顶升点及如何确定各点顶升量，目前通常做法是通过对不同顶升方案进行结构验算，来确定满足要求的顶升方案，当桥跨多、顶升量大时，符合更换要求的顶升方案有多种，采用人工计算比选确定最佳方案的工作量巨大。

为了快速、高效地实现最佳顶升方案的确定，针对连续梁桥中应用较多的“横桥向同步，纵桥向逐墩或多墩顶升”法，本文提出一种基于序列二次规划法的顶升方案确定方法，该方法可根据支座更换顶升需求进行顶升位置、次序和各支点顶升量的组合优化计算，从而确定最佳的顶升方案，且能高效地计算出各支点的极限顶升量，保证连续梁梁体各截面的安全，为顶升方案的设计提供参考。

1 优化法确定最佳顶升方案

结合工程实践及结构分析，最优顶升方案通常须满足以下3个条件：顶升量必须满足支座更换空间的要求及梁体受力的要求；辅助顶升点应尽量少；辅助顶升点应尽量地靠近目标顶升点[7]。上述条件不仅能满足施工及受力要求，而且能保证顶升工作量、千斤顶数量及临时支架量最少，是满足梁体安全条件下最经济顶升方案的必要条件。

1.1 优化思想

根据上述最佳顶升方案的条件，本文的优化思想如下：对n跨连续梁桥纵桥向的(n+1)排支座，依次编号为1，2，……，(n+1)号支点，设支点满足施工要求的顶升高度为Δ，设各支点单点顶升时的极限顶升量分别为：Δ1max，Δ2max，…，Δ(n+1)max。若Δ≤Δimax(i=1,2,…,n+1)对任一支点都成立，则顶升方案可为从1号到(n+1)号支点逐墩单点顶升。若对某些或全部支点有Δ>Δi max，则需在这些支点顶升时辅助顶升其他支点，以保证结构受力安全，为了考虑多点顶升时各支点顶升量对结构安全和线形的影响，将引入影响矩阵法。

1.2 影响矩阵法的应用

在应用影响矩阵法考虑多支点顶升量对各截面内力和位移的影响时，施调向量取各支点顶升量Δi(i=1,2…,n+1)，各关键截面(设为m个)的应力值为被调向量，第i号支点顶升单位量时，引起m个截面的变化效应记为：

{ki}={k1i,k2i,…,kmi}T

(1)

当有n+1个支点顶升单位量时，引起n+1个变化向量构成的矩阵，记为：

[K]={k1,k2,…,kn+1}=

(2)

顶升时，将各支点实际顶升量记为向量{xi}，当结构符合线性叠加原理时，在截面上产生的效应向量记为{D}，则满足：

[K]{xi}={D}

(3)

1.3 优化模型

1.3.1变量的选取

以i号支点为目标顶升支点为例，i号支点顶升目标高度Δii=Δ，将i号支点以外的支点顶升量作为优化变量，即有Δ1i,Δ2i,…,Δ(i-1)i,Δ(i+1)i,…,Δ(n+1)i共n个优化变量。

1.3.2目标函数

在顶升方案比选中，最佳方案的确定标准是顶升支点个数尽可能少和辅助顶升支点尽可能靠近目标顶升支点，为了实现这2个要求，目标函数取为：

minf(x)=φ1Δ1i+φ2Δ2i+…+φi-1Δ(i-1)i+

φi+1Δ(i+1)i+…+φn+1Δ(n+1)i

(4)

其中,Δji表示顶升i号支点时需要j号支点的辅助顶升量，φj(j=1,2,…,n+1)为权重系数，且有:

φj=Lji2

(5)

式中：Lji表示j号与i号支点之间距离。

权重系数越大，相应变量对目标函数影响越小，这意味着离目标支点越远的支点，需要的顶升量将越小或等于0。

1.3.3约束条件

为了确保结构受力安全，在每跨选取5个截面作为应力控制截面：1/4跨处截面、跨中截面及支点截面。对于n跨的桥梁，控制截面为m=4n+1个，要求所有控制截面的应力均满足规范要求，当顶升i(i=1,2,…,n+1)支点时，则应满足：

(6)

应力以压应力为正，拉应力为负。式(6)中：σy表示恒、活载及徐变作用下y(y=1,2,…,m)截面上缘或下缘正应力；σyi表示i号支点处梁体发生单位向上位移时引起y截面的正应力；[σt]表示混凝土容许拉应力值，对全预应力混凝土连续梁桥，取[σt]=0；[σc]表示混凝土容许压应力值。

根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》[8]中7.1.6规定，需考虑主拉应力是否满足要求，即有：

(7)

式中：σpy表示恒、活载及徐变作用下y截面上缘或下缘主拉应力；σpyj表示j号支点处梁体发生向上单位位移时引起y截面的主拉应力；fty为混凝土抗拉强度标准值。

顶升i号支点时，每个支点处辅助顶升值不应超过单点顶升时的极限顶升量，即优化变量还需满足：

0≤Δji≤Δjmax(j=1,2,…,i-1,i+1,…,n+1)

(8)

1.3.4极限顶升量优化模型

在主优化模型中，优化变量的上界由各支点单点顶升时的极限顶升量确定，为了计算各支点的极限顶升量，需建立另一个优化模型。该模型的实质是单变量优化，顶升i号墩时，以i号墩支点顶升量Δi为目标函数，约束条件与主优化模型相同，为控制截面的应力值满足规范要求，优化变量的上界取100 mm，根据以上条件建立优化数学模型如下：

ming(x)=-Δi

(9)

1.4 优化计算

本文优化变量为各支点顶升量，为了施工方便，考虑优化变量为整数，且由于本文的优化模型中，优化变量与目标函数及约束条件之间均成线性相关，即线性优化问题，因此采用求解整数线性规划的内点-分支定界法求解本文的优化数学模型。

本文所采用的优化与结构优化设计不同，其实质为针对结构的一种外荷载优化，并未改变结构自身特征，故本文优化中，只需对结构进行多次结构分析，得出各支点顶升单位量时的各截面应力值，综合成顶升量对截面内力的影响矩阵，供优化程序调用。在最优解搜索过程中，无需对结构进行重分析，因此优化计算速度较快。

2 优化算例

为验证本文优化方法的可行性，选取一座公路现浇连续箱梁桥和一座先简支后结构连续的小箱梁公路桥为依托工程。

2.1 算例概况

选取一座9×25 m的现浇连续箱梁桥为算例1，跨中断面形式如图1所示，混凝土强度等级为C50，采用φs15.2 mm低松弛预应力钢绞线，标准抗拉强度为fpk=1 860 MPa。横向设置2个支座，支座布置如图2所示，其中固定支座位于5号墩。

选取一座5×40 m先简支后结构连续预应力小箱梁桥为算例2，跨中断面形式如图3所示，混凝土强度等级为C50，采用φs15.2 mm低松弛预应力钢绞线，标准抗拉强度为fpk=1 860 MPa。横向4片小箱梁，每片小箱梁下设置1个支座，支座布置如图4所示，其中固定支座位于3号墩的2片中梁下。

2.2 有限元模型的建立

算例1和算例2均采用平面杆系单元建立有限元模型：算例1的连续箱梁桥全桥共计梁单元234个，支承单元10个，节点235个；算例2的小箱梁桥选取边梁作为不利截面进行分析，全桥共计梁单元200个，支承单元6个，节点201个。

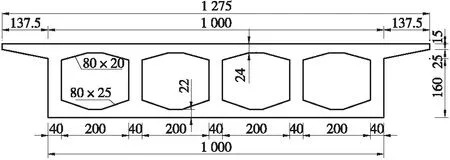
图1 现浇连续箱梁截面示意图(单位： cm)

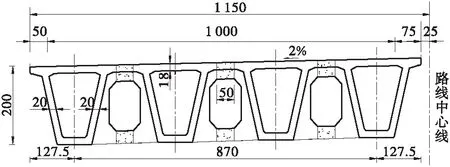
图3 小箱梁桥截面示意图(单位： cm)

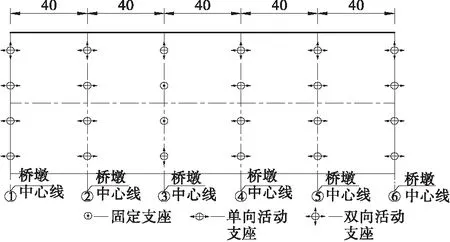
图4 小箱梁桥支座示意图(单位： m)

2.3 计算结果

在支座最佳顶升方案确定的主优化模型中，对算例1的连续梁桥目标顶升量分别取20、25、30 mm 3种情况进行优化计算，优化结果见表1～表3。对算例2的连续小箱梁桥，目标顶升量取20 mm进行优化计算，结果见表4。在表1～表4中，无数值的位置表示顶升目标支点时，该位置的支点不需要辅助顶升。从表1～表4中可以看出，当考虑权重系数时，优化结果能很好地达到预期目标，即当某号支点顶升到位时，距支点越远的支点需要顶升量越小或为0。同时，数据显示某支点顶升到位时，其引起的顶升点为相邻支点，不会隔跨，在满足结构受力情况下，降低了施工的复杂程度。

为了验证在顶升方案优化模型中考虑权重系数的必要性，在不考虑权重系数的情况下对算例1在目标顶升量为25、30 mm时进行顶升方案分析，结果见表5和表6。该结果也是满足结构受力的另一种顶升方案，但从表5与表2及表6与表3的结果对比中可以看出，若不考虑权重系数，某支点顶升到位时，需要其他辅助顶的支点更多，如在表5中，对4号支点一次顶升到25 mm时，所必须顶升的不仅有相邻的3号、5号支点，还包括与4号支点相隔3跨的1号和7号支点，且相隔越远，需要顶升量很少。显然这与表2在同样25 mm情况下的优化结果相比，增加了顶升支点的数量，施工时需要更多的顶升设备，增加了施工的复杂程度。上述对比结果说明考虑权重系数时优化得到的顶升方案，不仅能满足结构受力需求，同时可使施工最为便捷，因此在最优顶升方案的计算中，考虑权重系数是十分有必要的。

表1 算例1目标顶升量Δ=20 mm时优化结果顶升支点其余支点各最优顶升量/mm123456789101△23△336△546△556△565△675△685△693△310△ 注:无数值表示不需顶升,△表示目标顶升点及顶升量20 mm。

表2 算例1目标顶升量Δ=25 mm时优化结果顶升支点其余支点各最优顶升量/mm123456789101△227△835△14415△4515△464△1574△15814△598△7102△ 注:无数值表示不需顶升,△表示目标顶升点及顶升量25 mm。

表4 算例2目标顶升量Δ=20 mm时优化结果顶升支点其余支点各最优顶升量/mm1234561△22△737△646△757△62△ 注:无数值表示不需顶升,△表示目标顶升点及顶升量20 mm。

表5 算例1不考虑权重系数φ时目标顶升量Δ=25 mm的优化结果顶升支点其余各支点辅助顶升量/mm123456789101 △226△81310△94 29△925 10△96 9△107 29△928 9△109 18△610 2△ 注:无数值表示不需顶升,△表示目标顶升点及顶升量25 mm。

表6 算例1不考虑权重系数φ时目标顶升量Δ=30 mm的优化结果顶升支点其余各支点辅助顶升量/mm123456789101△428△14313△144113△1325315△15046415△1537213△131814△13914△8104△ 注:无数值表示不需顶升,△表示目标顶升点及顶升量30 mm。

对比表5与表2及表6与表3还可以看出，同一支点目标顶升量相同时，可以有不同的满足结构受力安全的顶升方案，若采用试算法确定顶升方案，需进行大量计算比选，工作量大。

表7和表8分别为算例1和算例2的极限顶升量优化结果，从表中可以直观地看出各支座在进行单点顶升时的最大容许顶升量，为选取顶升施工方案提供数值计算依据。

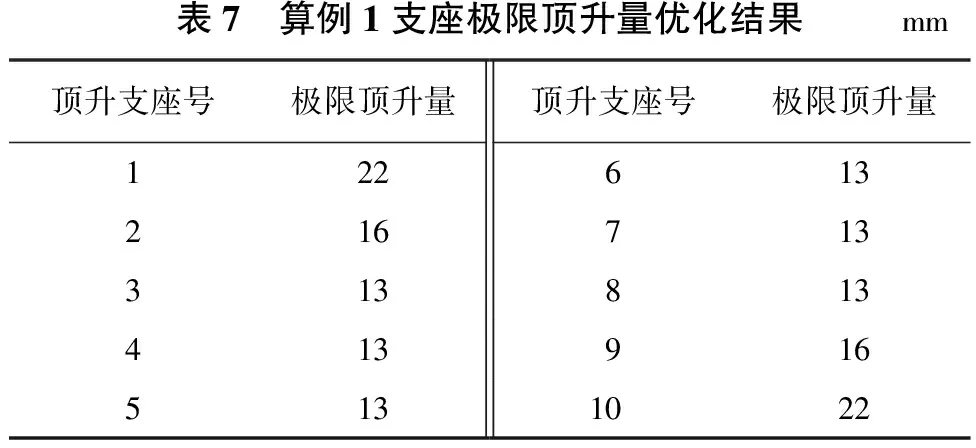
表7 算例1支座极限顶升量优化结果mm顶升支座号极限顶升量顶升支座号极限顶升量1226132167133138134139165131022

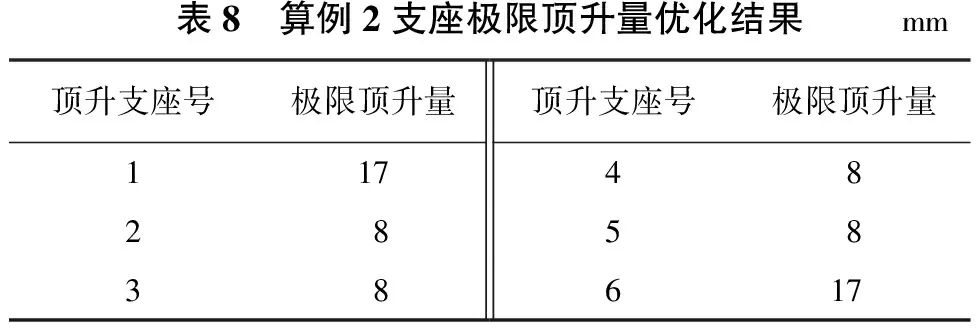
表8 算例2支座极限顶升量优化结果mm顶升支座号极限顶升量顶升支座号极限顶升量11748285838617

3 结论

本文针对连续梁中应用较多的“横桥向同步，纵桥向逐墩或多墩顶升”法，提出一种最佳顶升方案确定的优化算法，通过2个算例验证了该方法在确定最佳顶升方案时的高效性和可行性，并得出结论如下：

1) 本文首次将优化方法引入“横桥向同步，纵桥向逐墩或多墩顶升”法，以各支点顶升量为优化变量、以梁体控制截面受力满足规范要求为约束条件、以顶升位置最少为目标函数，建立优化数学模型，实现了快速得出支座更换的最优顶升方案。

2) 采用了影响矩阵法的思想，从结构有限元分析程序中提取应力影响矩阵导入优化程序进行计算，避免了反复调用结构分析程序的过程，提高了计算效率。

3) 本文优化模型中，目标函数引用了权重系数，并通过算例优化结果的对比，体现了考虑权重系数影响的优化结果更贴近理想结果，方案更合理。

4) 对于通用跨径的简支变连续梁桥，可将通用截面形式建立为数据库文件，使用本文顶升方案确定方法编制一套系统程序，仅输入不同的跨径和跨数就可进行顶升方案优化计算，快速得出顶升方案，应用前景广阔。