动态DNA步行者折纸计算模型——求解可满足性问题

斯燕方 殷志祥 崔建中 杨 静 唐 震

（1.安徽理工大学数学与大数据学院；2.上海工程学院数学、物理和统计学学院 上海201620；3.安徽理工大学电气与信息工程学院；4.淮南联合大学计算机系 安徽淮南 232001）

一、引言

2006 年，Rothemund 等首次提出 DNA 折纸术[1]，该方法不同于传统自组装（自上而下的组装），而是将一条长M13mp18噬菌体DNA链作为脚手架链来回折叠,并利用200多条订书钉链将形状固定。成功得到了正方形、矩形、五角星、笑脸和三角形等精细复杂的二维结构，随后许多更加复杂多样的纳米结构[2-3]不断被设计并组装出来。Andersen E S 和钱璐璐等分别用DNA 折纸术折叠出海豚结构的校徽[4]和中国地图[5]。文献[6]用DNA折纸折叠出光学超分子自组装的支架。文献[7]利用DNA折纸自组装折叠出蒙娜丽莎、公鸡等图案。文献[8]构建了一个可编程的DNA折纸平台，用来组织用于膜融合的陷阱。文献[9]用DNA折纸纳米结构使肿瘤细胞中的细胞摄取和转移可视化。

链置换技术是利用DNA 分子单链间的粘贴，通过加入输入链来释放另一条DNA 链。这种技术具有自引发性，灵敏性和准确性等特点。2000年，文献[10]率先在DNA纳米技术上使用立足点链置换反应。随后，文献[11]利用DNA链置换，构建了一种可以反复读取和输入的存储器。文献[12]介绍了基于DNA链置换反应的编码器逻辑运算模型研究。文献[13-15]利用DNA链置换分别设计了不同的逻辑门模型。

Seeman 和 Sherman 于 2004 年推 出的第 一款 DNA 步行者是设计用来沿着一条一维（1D）轨道行走的，该轨道由三股突出的单链DNA 构成[16]。DNA 步行者也可以在由DNA折纸或DNA修饰的平面组成的二维轨道上移动。第一个二维DNA 步行者的例子是DNA 蜘蛛[17]。最近还引入了在三维轨迹上横穿的随机DNA步行者[18,19]。2010年，文献[20]设计了三手四足的DNA步行者，利用链置换驱动DNA步行者沿轨道顺时针行走，运输金纳米颗粒。文献[21]将DNA步行者应用于解决Petri网问题。文献[22-25]主要将DNA步行者应用到传感器中，能够实现信号的放大作用。文献[26,27]详细介绍了DNA步行者的研究进展与新兴生物分析应用。

布尔可满足性问题（简称SAT问题）是一个著名的判定问题，不仅在数理逻辑和计算理论等方面有着举足轻重的研究地位，而且在实际生产领域具有很高的应用价值。1995年Princeton大学的Lipton通过DNA计算解决可满足性问题[28]；随后Head 等人提出质粒DNA 分子解决可满足性问题[29]文献[30-32]分别介绍了三种不同的可满足性问题的计算模型。

本文构建了一个动态DNA步行者折纸计算模型，该模型由三部分组成：步行者、轨迹及燃料链。步行者行走的轨迹是在DNA折纸上固定的发夹结构形成的。步行者通过碱基互补固定在DNA折纸的起始链上，当加入起始链的补链才会释放步行者参与反应。燃料链也是发夹结构，能通过链置换反应催动步行者向前行走。步行者行走的轨迹发夹呈二叉树结构分布在DNA折纸基底上，最后的一个分支上的发夹比前面的发夹在3′端多一段可识别的粘性末端，且DNA折纸基底上的所有发夹的环部区域都有特定的刻痕酶切割位点。在应用该模型解决问题时，可以先根据约束条件对不满足条件的路径通过可识别的粘性末端打开发夹形成稳定的双链结构，以此来堵塞不满足条件的路径。由于步行者无法通过堵塞的路，则DNA步行者通过的路都是满足约束条件的可行解所对应的路。最后通过刻痕内切酶和链置换反应很容易获得需要的短链结构，使用凝胶电泳读解即可。此模型通用性很高，可以很好地解决很多问题NP问题。本文我们以该模型解决一个3-SAT 问题为例，用DNA 发夹结构铺设了一条一个入口和八个出口的二叉树结构，很好地解决了三个变量的可满足问题。

可满足性问题可表述为：由若干个析取范式合取构成的范式叫做合取范式，如，其中由若干个合取范式析取构成的范式叫做析取范式，如其中表 示互为否定，它们的取值或是0或是1，“1”表示值为真，“0”表示值为假。可满足性问题是指对于给定的一个含有个变量的合取范式或者析取范式，是否存在一组或多组变量的取值使得该范式的真值为1。如果中的变量个数都小于或等于K个，那么称其为K-可满足性问题。

二、动态DNA步行者折纸计算模型

该模型由三部分组成，分别为DNA折纸基底、固定在基底上的DNA结构T和添加的DNA结构T*。

图1 DNA折纸基底及布局

折纸基底（图1a）是由许多短的订书钉链将一条M13长链折叠而成的矩形结构，在折纸基底上有带有粘性末端的延伸单链，用来固定发夹结构。设计好的DNA发夹结构以图1（b）的布局铺设在DNA折纸上，形成步行者要行走的轨道。轨道发夹用T（紫色）和Ti（绿色）表示，在加入燃料链后步行者可以通过打开发夹结构向前行走。其中Ten（红色）为初始单链，步行者开始是固定在Ten上的，加入Ten的补链能置换出步行者，使释放的步行者参与反应。Ti与T是结构上基本相同的发夹结构，发夹Ti的3'端比发夹T多出一段可识别的延伸短链，分布在轨道的最后一个分支。

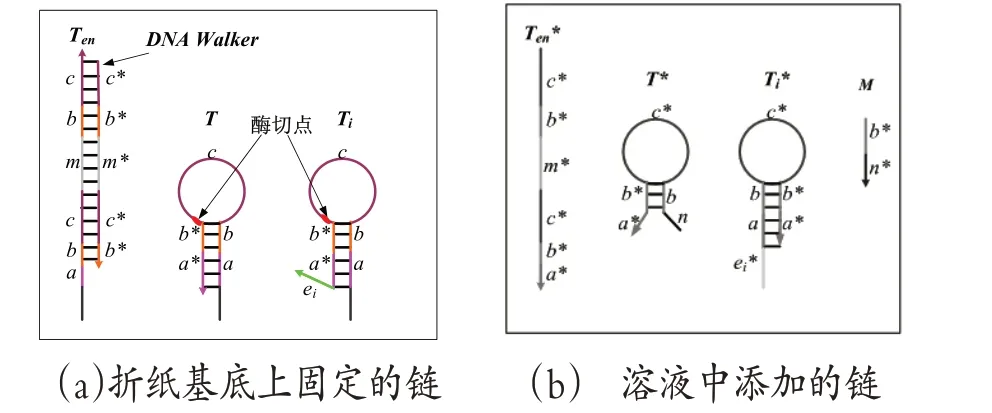
图2 链的组成与结构

图2（a）为固定在DNA折纸基底上的DNA链，这些链铺设成了DNA步行者行走的轨道。图2（b）为相应的补链，这些链是按实验要求依次添加的链。Ten为轨道的起点，DNA步行者通过部分碱基互补固定在Ten上，当在溶液中添加Ten*时，通过链置换反应便可释放DNA步行者。链T和Ti铺设在轨道上，形成DNA步行者行走的路，Ti在3'比T多出一段可识别的单链结构，每个路口对应不同的ei，映射为问题的不同可能解。链T和Ti上c 段都有特殊的酶识别位点，当形成双链的状态下，加入切刻内切酶（切刻内切酶是一种限制性核酸内切酶，它特异性的识别双链DNA中的一段核苷酸序列，并只对其中的一条链进行切割）时可从酶切点切割链T和Ti。链T*能与打开发夹状态的T和Ti形成部分双链，是DNA步行者行走的燃料链，当加入切刻内切酶和链M能置换出被切刻的部分。Ti*能通过ei*识别Ti上的延伸短链ei，从而打开对应的Ti发夹形成稳定的双链状态。由于此时的双链状态趋于稳定，加入切刻内切酶和链M也无法置换出被切刻的部分。具体步骤见图3。

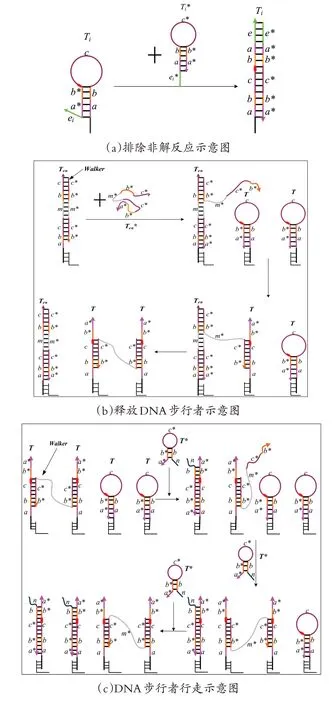
图3 反应过程示意图

反应的具体过程如图3 所示。反应的第一步为排除非解（图3a），加入非解所对应的发夹Ti的补链Ti*，发夹Ti*的粘性末端ei*通过识别ei打开发夹Ti，并与Ti形成稳定的双链结构，这些稳定的双链将不会再与步行者发生链置换反应，成功堵塞住不满足条件的路径，即步行者将不会走过非解所对应的路。反应的第二步是释放步行者（图3b），第一步删除非解后，加入Ten*，Ten*上的a*首先与Ten上的a部分结合并逐步置换出Ten上的步行者，并与Ten形成稳定的双链结构，部分释放的步行者上的c*段与邻近发夹c段互补并打开发夹T，接着全部从Ten上释放的步行者的5'的c*段与第二个发夹c段互补打开第二个发夹T，由此，步行者固定到两个相邻的发夹T上，成功进入轨迹。反应的第三步是加入燃料链T*（图3c），在步行者开始打开第二个发夹T时加入燃料链T*，由于发夹T*的a段与完全打开的发夹T的a段互补并发生链置换作用，可以置换出步行者后面的那条腿，解绑的后腿继续打开第三个发夹T，由此催动步行者一步步向前行走。由于燃料链T*只能与完全打开的发夹T发生反应，则整个反应中都是先置换步行者位于后面的那条腿，且反应不可逆，这能确保步行者是始终向前运动的。步行者能沿着其中一条没有被堵塞的路向前走至出口，且步行者走过的路径上的发夹都形成部分双链结构。第四步是加入切刻内切酶和链（图3d），由于此时步行者走过的链T和T i都是部分双链状态。加入刻痕内切酶，刻痕内切酶只能对双链DNA中含有刻痕切刻位点的那一条链进行切割。由于发夹T上有刻痕切刻位点，形成双链后加入切刻内切酶，则可对T从切割位点进行切割。加入的链能通过n*识别短链n从而置换出我们所需要的链I i。此时步行者走过的每条路径均对应于所求问题的一个可行解。

溶液中的单链只有步行者与切割下来的对应于可行解的链I i，进行凝胶电泳即可读出可行解。

三、实例分析

此动态DNA 步行者折纸计算模型可用于解决很多问题，本文以求解可满足性问题为例。

（一）算法。对于含3 个变量、合取范式的可满足问题，其可能解的个数为23共8种，则Ti(i=1,2,…,7)，其解映射为二叉树结构，如图4所示。对于ei(i=1,2,…,7)我们设计了八种结构表示为对应于可满足性问题的8个可能解0(0,0,0)、1(0,0,1)、2(0,1,0)、3(0,1,1)、4(1,0,0)、5(1,0,1)、6(1,1,0)、7(1,1,1)，ei*是与ei互补的短链。则产生8种发夹结构Ti(i=1,2,…,7)和8种发夹结构Ti*(i=1,2,…,7)。

图4 所有可能解的二叉树结构示意图

步骤1：排除非解；

步骤2：DNA步行者的行走；

步骤3：切割短链Ii；

步骤4：读解。

（二）生物操作。步骤1：分析第一个子句知满足x∨y为假的为，则加入e0、ei对应发夹T0、Ti的补链发夹T0*、Ti*，分析第二个子句知满足为假的为则加入e4、e6对应发夹T4、T6的补链发夹T4*、T6*，分析第三个子句知满足为假的为则加入e2对应发夹T2的补链发夹T2*。通过此步骤即可排除掉所有非解。

步骤2：加入Ten*，释放出DNA 步行者，然后在溶液中加入T*，T*作为燃料链推动DNA 步行者向前行走。由于DNA步行者无法通过非解所对应的路L0、L1、L2、L4、L6，所以DNA步行者走过的均为可行解所对应的L3、L5、L7之中的一条路。

步骤3：待DNA步行者走过Ti链，加入切刻内切酶和链M，切割并置换出I3、I5、I7这三条链。

步骤4：通过凝胶电泳读出链I3、I5、I7。则该可满足性问题的解为3(0,1,1)、5(1,0,1)、7(1,1,1)。（三）结果显示。满足该可满足性问题的其中的一个解3(0,1,1)，如图5所示：

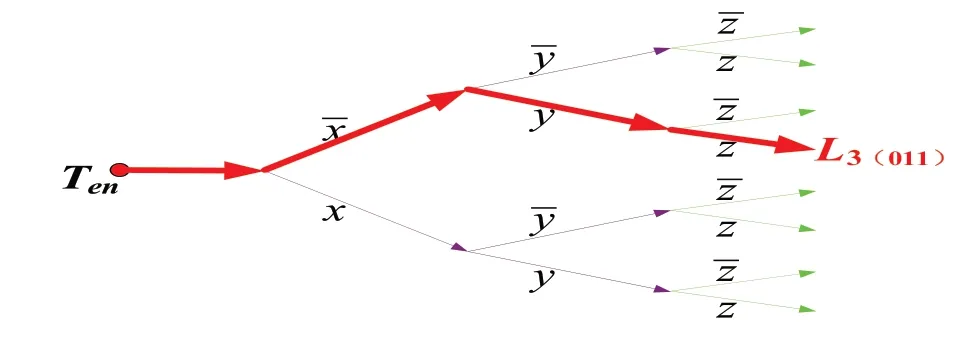
图5 3(0,1,1)解示意图

四、结语

本文将DNA 折纸术和链置换技术催动的DNA 步行者结合，构建了一个动态DNA步行者折纸计算模型。DNA步行者是一类独特的动态DNA装置，它可以沿着一维、二维或三维轨迹移动步行者，文中设计的沿着二维轨道运动的双足步行者具有高自由度和高行进性，且结构简单，在步行者运动的过程中不用逐步加入燃料链，这使得该模型操作更加简单易行。且此模型通用性高，可解决许多NP问题，文中用此模型成功解决了可满足性问题，不同于以往解决可满足性问题先得出所有可能解再根据约束变量一一排除的方法，此模型第一步就是先排除非解，则反应后得出的解均为问题的可行解，这大大简化了后期筛选的工作。同时随着问题变量的增多，实验中发夹T的种类并不会随之增多，只需要相应的增加可识别的粘性末端e的种类即可，这给实验带来极大的简化，对于多个变量的可满足问题甚至是整数规划问题等都可以很好地解决。但问题仍然存在，随着变量的增多，折纸基底上的发夹数量相应增多，这势必需要更大的折纸基底结构，相信随着DNA 自组装技术的发展，该问题可以得到解决。