一种最小加权延迟问题的整数规划算法

黄光泉 丁柏圆

摘要：在最小延迟问题的基础上，对最小加权延迟问题（MWLP）进行了简要介绍，对已有的算法进行了分析，对使用整数规划算法解决近似问题的方法进行了研究。在此基础上，提出了一种解决最小加权延迟问题的整数规划算法，详细介绍了该算法的数学模型建模和实现。通过随机生成的实验数据对该算法进行了验证，结果表明，该算法在确保了较高的准确度的前提下，时间效率上相较穷举法得到了较大的提升，在实际场景中具有应用价值。

关键词：最小延迟问题；最小加权延迟问题；整数规划

中图分类号：TP312文献标志码：A文章编号：1008-1739（2020）22-71-3

0引言

指挥调度是部队演习和实战过程的关键点之一，最小加权延迟问题（MWLP）在导弹训练调度等场景中有着很大的应用前景。作为一个复杂的非确定性问题，由Kousoupias[1]首次提出。此后，吴邦一[2]提出了一种动态规划算法以解决MWLP问题，但是该方法只适用于部分特殊的场景。Wei等[3]尝试使用启发式算法解决MWLP问题，并对比分析了5种常见启发式算法的效果和效率。Miliotis[4]尝试使用整数规划算法解决与MWLP问题近似的旅行商问题（TSP），Gozde等[5]提出了一种新的整数规划方法解决TSP问题，Francisco等[6]更进一步将整数规划应用于最小延迟问题（MLP），而MLP问题可被视为各点权值相等的MWLP问题。这些研究通过各种方法解决MWLP问题及相关问题，给后续研究提供了借鉴和启发。本文在Francisco等[6]工作的基础上，对其提出的数学模型进行了扩展，从而可以直接使用整数规划解决MWLP问题，并对该模型和算法进行测试，证实了其在准确度和时间效率上的使用价值。

1 MWLP问题定义

2整数规划数学模型

一般的线性规划问题中，最优解可能是整数，也可能不是，但在实际应用中，常常要求变量必须是整数。比如，購买机器的台数、携带物品的件数、车辆调度的车辆数等，这类特殊的线性规划即是整数规划。许多组合优化、图论和计算逻辑问题都可以归结为整数规划问题，而MWLP就属于图论中的问题。Francisco等[6]提出了使用整数规划来解决MLP问题，受此启发，提出了一种解决MWLP问题的整数规划算法。

2.1 MWLP问题多层网络表示

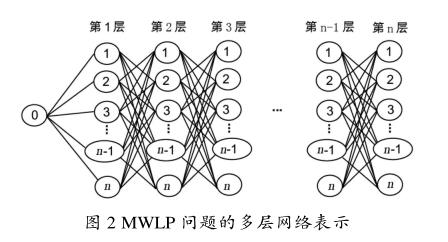
MWLP问题可以使用多层网络表示，如图2所示，共有+1个节点，+1个层次，层次代表路径上的先后顺序，起点单独放在第0层，是确定的。对于MWLP问题，优化目标就是从除起点之外的其他层各选一个城市，使得加权延迟之和最小。同时需要保证每层只有一个城市，每个城市只出现在一层。

2.2数学模型

该模型在Francisco等的工作[6]中的数学模型1的基础上进行了拓展，如式（2）所示，定义代表从顶点到顶点的时间代价，其中，是在顶点处的服务时间，是从顶点到顶点的过程中所用的时间，为顶点的权重，

3实验和分析

3.1实验设置

为了验证上面所提出的整数规划算法是否可行，本节使用随机生成的数据对该算法进行测试。为了尽可能模拟实际生活中可能遇到的场景，实验数据已经被限定需要满足三角不等式，或者可以认为所有的数据都对应平面上不重复的实际点。各顶点的权值从标准正态分布中随机采样获取，并且满足每个顶点的权值大于0且小于1。

3.2结果和分析

实验结果如表1所示。从准确度的角度分析，因为穷举法是从所有可能的路径中挑选一条最优的路径，所以其准确度均为1.0，而整数规划算法虽然不能达到最优，但是其准确度接近0.85，和穷举法的结果很接近。并且可以看出，顶点规模对于准确度没有明显的影响，这对于实际应用有着重要的参考意义。

使用穷举法时，顶点规模从7～9变化的过程中，所用时间并没有呈指数上升，应该是由于顶点规模太小，导致算法运行所消耗的时间同程序自身运行时所消耗的固有时间相比很小，从而导致顶点规模变化对所用时间影响有限。

从所用时间的角度分析，在顶点规模≤9的情况下，穷举法和整数规划算法没有太大差别，这时可以考虑使用穷举法以得到最优解。但是在规模>9时，如图3所示，穷举法所用时间会呈指数上升，而整数规划算法则大体呈线性上升的趋势，此时可以考虑使用整数规划算法在可承受的时间内得到一个较优解。

4結束语

提出了一个整数规划算法用来解决MWLP问题，使用限定条件的模拟生成的数据进行了实验，证明了整数规划算法解决MWLP问题是可行的，在较大规模的问题上，该算法可以在得到一个较高精确度的可行解的前提下，大幅减少所用时间。该算法具有广泛的实际应用价值，未来可应用于导弹训练调度等具体的指挥训练场景，从而节省资源、提高效率。

参考文献

[1] KOUTSOUPIAS E，PAPADIMITRIOU C，YANNAKAKIS M.Searching a Fixed Graph[J].Lecture Notes in Computer Science，1996：280-289.

[2] WU B Y. Polynomial Time Algorithms for Some Minimum Latency Problems[J].Information Processing Letters，2000，75（5）：225-229.

[3] WEI Z Q，H.MACGREGER M. Heuristic Approaches for Minimum Weighted Latency Problem[C]/International Conference on Machine.Paris：IEEE，2017：552-556.

[4] MILIOTIS P.Integer Programming Approaches to the Travelling Salesman Problem[J].Mathematical Programming， 1976，10（1）：367-378.

[5] ONDER G， KARA I， DERYA T.New Integer Programming Formulation for Multiple Traveling Repairmen Problem[J]. Transportations Research Procedia，2017，22：355-361.

[6] FRANCISCO A B，ADA A，IRMA G.Two Improved Formulations for the Minimum Latency Problem[J].Applied Mathematical Modelling，2013，37（4）：2257-2266.