一道不等式证明题的解法赏析
2020-04-01 04:14李宁英
数理化解题研究 2020年10期
李宁英
(新疆克拉玛依市第一中学 834000)
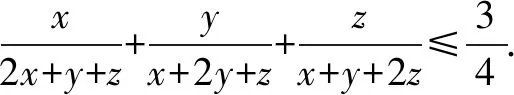
方法1恰当设元后利用平均值不等式进行证明.
设2x+y+z=a,x+2y+z=b,x+y+2z=c,则a,b,c均为正实数,
当且仅当a=b=c,即x=y=z时等号成立.
评析方法1利用平均值不等式证明的关键是分拆和转化,直接不好分拆时考虑重新设元,将分母设元后,将分母变简单,拆项后利用均值不等式,注意均值不等式等号成立的条件.
方法2恰当设元后将要证的不等式等价转化.
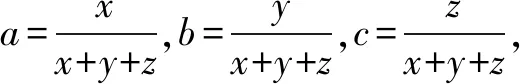
转化为只要证
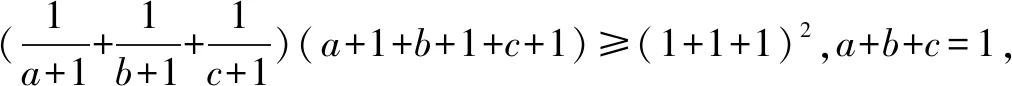
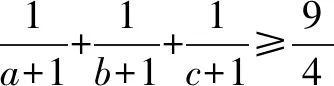
原不等式得证.
评析方法2通过观察原式的结构,进行设元,将原不等式进行等价转化,将要证的不等式变得简洁,然后再利用柯西不等式进行证明.
方法3利用调和平均数与算术平均数的关系证明.
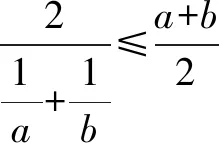
当且仅当a>0,b>0,a=b时等号成立.
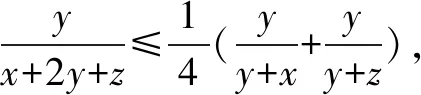
当且仅当x=y=z时等号成立.
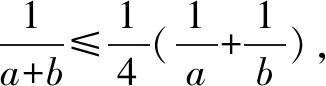
方法4构造两组数,利用排序不等证明.
不防设x≥y≥z>0,
则2x+y+z≥x+2y+z≥x+y+2z,
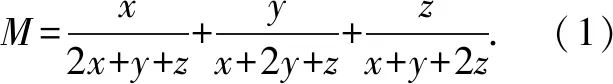

两组数及排序不等式“逆序和”小于等于“乱序和”可得:
由2(1)+(2)+(3)得
当且仅当x=y=z时等号成立.
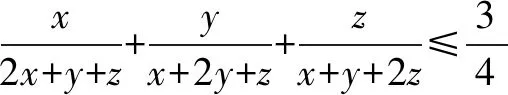
评析应用排序不等式,构造出恰当的两个便于排序的数组是关键,一般都采用“不防设”的技巧进行排序,借助这种大小顺序进行适度的“放缩”,再利用不等式的性质从而得证.
方法5巧妙拆分后利用柯西不等证明
+(x+2y+z)+(x+y+2z)]
当且仅当x=y=z时等号成立.
评析根据不等式的结构特征,观察左边每一项分子、分母关系,进行拆分,约掉分子、分母的共同因式,然后再利用柯西不等式进行证明.
通过不等式证明的五种方法,希望对不等式证明中所蕴含的数学思想方法加以梳理,从而找到解决不等式证明的一般方法,大家在今后处理类似问题时加以运用和体会.
猜你喜欢
中学生数理化·七年级数学人教版(2021年11期)2021-12-06
中学生数理化·七年级数学人教版(2020年11期)2020-12-14
语数外学习·高中版中旬(2020年2期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
中学生数理化·七年级数学人教版(2019年11期)2019-09-10
小天使·五年级语数英综合(2017年11期)2017-11-30
高中生学习·高三版(2017年6期)2017-06-12
中学生数理化·八年级数学人教版(2016年5期)2016-08-23
中学生数理化·八年级数学人教版(2016年5期)2016-08-23
中学生数理化·八年级数学人教版(2016年5期)2016-08-23

