碳质物拉曼光谱变质温度计及其在造山带热结构重建与演化中的应用*

黄保有 张波** 张进江 谭舟 张磊 陈思雨 李晓蓉

1. 造山带与地壳演化教育部重点实验室，北京大学地球与空间科学学院，北京 1008712. 岩石圈演化国家重点实验室，中国科学院地质与地球物理研究所，北京 100029

基于变质岩石内特定矿物组合估算变质温度和P-T-t轨迹是揭示造山带热演化过程的重要途径(Spear, 1995；魏春景等，2001；Wuetal., 2002；Liuetal., 2004；刘福来等，2006；吴春明等，2007；Weietal., 2009)，然而，在很多变质带中常缺乏可用于估算变质温度的合适矿物组合，碳质物拉曼光谱温度计可作为一个新的方法给予补充(Beyssacetal., 2002a；Rahletal., 2005；Aoyaetal., 2010)。碳质物广泛存在于变质沉积岩中，在成岩和变质过程中逐渐转变为石墨，即石墨化(Buseck and Beyssac, 2014)，在石墨化过程中，碳质物的结晶度逐渐提高，是岩石变质程度(尤其是温度)的可靠指标。

对于碳质物结晶度与温度关系研究，早期的学者通过X射线衍射(XRD)技术进行观测(Itaya, 1981；Yuietal., 1996；Beyssacetal., 2002a；Rahletal., 2005；Aoyaetal., 2010；Lahfidetal., 2010；Kouketsuetal., 2014)，随后通过镜质体反射率(French, 1964；Landis, 1971；Kisch, 1980；Itaya, 1981；Tagiri, 1981；Mori and Taguchi, 1988；Georgeetal., 2001)以及利用高分辨率透射电子显微镜(Buseck and Huang, 1985；Jehlicka and Rouzaud, 1990；Beyssacetal., 2002b；Nakamura and Akai, 2013)，这些研究结果表明碳质物结晶度与变质温度之间具有正相关性。近年来，高空间分辨率激光拉曼光谱定量分析技术已成为表征碳质物结晶度的有效工具(Beyssacetal., 2002a)。Beyssacetal.(2002a)利用该技术测量变质岩中碳质物的结晶度，并提出碳质物拉曼光谱温度计，由于方法简单实用，引起广泛关注(d’Alessioetal., 2003；Satoetal., 2006；Yamadaetal., 2007；Robertetal., 2010；Tagami, 2012；Cooperetal., 2013； Yoshidaetal., 2016；Laurentetal., 2018)。随后有研究者基于实验和天然样品的分析，对该温度计进行了修订和扩展，提出了不同版本的变质温度计算公式，拓宽了该方法的使用范围(Rahletal., 2005；Aoyaetal., 2010；Lahfidetal., 2010；Kouketsuetal., 2014)。作为新型温度计，其影响因素也被关注，在低温变质环境(温度<300℃)，碳质物的结构不仅受温度影响，还受变质压力、变质持续时间、变形、催化物质和碳质物前体类型的影响(Landis, 1971；Diesseletal., 1978；Bonijolyetal., 1982；Wopenka and Pasteris, 1993；Wadaetal., 1994；Bustinetal., 1995；Suchyetal., 1997；Buseck and Beyssac, 2014)。由于很难从天然岩石样品中评估每一种因素的影响(Lahfidetal., 2010)，因此目前尚未建立统一的碳质物拉曼光谱温度计计算公式。尽管如此，激光拉曼光谱可以原位、准确、高效的获取碳质物结晶度相关参数进而估算变质峰期温度，解决了传统方法繁琐、费时等问题，大大提高了工作效率(Beyssacetal., 2002a)。相比基于特定矿物组合和矿物组成的温度计(魏春景等，2001；Wuetal., 2002；吴春明等，2007；Weietal., 2009)，拉曼光谱温度计在以下几方面极具优势：(1)碳质物广泛存在于变质沉积岩中，岩片及岩石薄片均可用于拉曼光谱分析(Beyssacetal., 2002a；Rahletal., 2005；Aoyaetal., 2010)；(2)激光拉曼光谱可对岩石薄片中的碳质物进行原位无损的探测分析，可同时观测到碳质物与周围矿物间的结构、构造与组合关系，便于将构造与变质温度与事件相关联(Kouketsuetal., 2014)；(3)激光拉曼光谱分析准确度高(分辨率为～1μm)、效率高(单点光谱获取时间～10s)，因此激光拉曼可在短时间内获取大量、乃至海量光谱测量数据，以消除测量样品的异质性(Aoyaetal., 2010)；(4)变质过程中碳质物石墨化具有不可逆性，碳质物结构记录峰期变质，不会遭受后期退变质改造(Buseck and Beyssac, 2014)，因此碳质物拉曼光谱变质温度计估算的温度为峰期变质温度(Beyssacetal., 2002a；Rahletal., 2005；Aoyaetal., 2010)。

1 碳质物拉曼光谱温度计原理与方法

变质沉积岩中碳质物随变质温度增加而逐渐石墨化是碳质物拉曼温度计的理论基础(Beyssacetal., 2002a, 2004；Rantitschetal., 2004)。沉积岩通常含有痕量的有序度低、结晶程度低的碳质物，但随变质程度的增加，碳质物逐渐转变为有序度高的结晶石墨(Grew, 1974；Pasteris and Wopenka, 1991；Wopenka and Pasteris, 1993；Yuietal., 1996)。通过激光拉曼光谱获取碳质物结晶程度相关量化参数，再根据结晶度与温度间的相关公式(Beyssacetal., 2002a；Rahletal., 2005；Aoyaetal., 2010；Lahfidetal., 2010；Kouketsuetal., 2014)，可估算变质岩石变质温度(Beyssacetal., 2002a；Rahletal., 2005)，值得注意的是，由于石墨化过程的不可逆性(碳质物倾向于热力学稳定相(石墨))，即碳质物结构对退变质不敏感，因此利用该方法计算出的温度可以被解释为样品整个变质过程中达到的变质峰期温度(Landis, 1971；Pasteris and Wopenka, 1991；Wopenka and Pasteris, 1993；Wadaetal., 1994；Beyssacetal., 2002a, b, 2004, 2007；Rahletal., 2005；Negroetal., 2006；Angiboustetal., 2009；Gabaldaetal., 2009；Lahfidetal., 2010)。

1.1 碳质物拉曼温度计原理

拉曼光谱是一种散射光谱，当激光发出的入射光子与作为散射中心的样品分子相互作用时会产生弹性碰撞与非弹性碰撞，在非弹性碰撞过程中，入射光子与分子之间存在能量交换，导致入射光子方向与频率发生改变，这种散射称之为拉曼散射。拉曼散射依据样品分子原始能级状态又可进一步分为斯托克斯散射与反斯托克斯散射(图1)。根据玻尔兹曼定律，在室温下，分子绝大多数处于振动能级基态，所以拉曼光谱记录的一般都是斯托克斯散射过程(Reed and Simon, 1979；贺福，2005；张延会等，2006)。

图1 拉曼散射示意图Fig.1 Sketch diagram of Raman scattering

在拉曼光谱中横坐标拉曼位移是斯托克斯和反斯托克斯散射光频率与入射光频率之差(△v)，拉曼位移取决于分子振动能级的变化，它与入射光频率无关，不同的化学键或基态有不同的振动方式，决定了其能级间的能量变化，因此与之对应的拉曼位移也具特征(贺福，2005；张延会等，2006)，这是拉曼光谱进行分子结构定性分析的理论依据。拉曼光谱的纵轴代表谱峰强度，谱峰的强度与产生谱峰特定物质的浓度有关(Tuinstra and Koenig, 1970；张延会等，2006)。

石墨为层状结构，共有六支色散曲线(图2a)(Malardetal., 2009)，分别为三个光学支(面内纵向光学支iLO、面内横向光学支iTO和面外横向光学支oTO)和三个声学支(面内纵向声学支iLA、面内横向声学支iTA和面外横向声学支 oTA)。面内(i)和面外(o)分别为原子的振动方向平行或者垂直于石墨烯平面，纵向(L)和横向(T)即为原子的振动方向平行或者垂直于A-B碳碳键的方向(吴娟霞等，2014)。这些晶格振动产生的色散曲线表示出各种振动模式的频率与波矢散射的关系(图2a)。

碳质物典型的拉曼光谱由一级序区(1100～1800cm-1)和二级序区(2500～3100cm-1)两部分组成(Tuinstra and Koenig, 1970；Nemanich and Solin, 1979)(图2c)。在一阶序区，碳质物拉曼光谱特征峰包括D1(D)峰(1350cm-1)、G峰(1580cm-1)和D2(D’)峰(1620cm-1)，结晶度低的碳质物中通常还有D3峰(1520cm-1)和D4峰(1245cm-1)，其中，G峰代表石墨峰，D峰代表缺陷峰。二阶序区对应于倍频和散射组合，主要为S1峰(2700cm-1)和S2峰(2900cm-1)(Nemanich and Solin, 1979；Wopenka and Pasteris, 1993)。

图2 碳质物拉曼光谱产生原理(a)单层石墨烯振动曲线(据吴娟霞等，2014修改)；(b)石墨晶体空间群振动模式及振动频率(据贺福，2005)；(c)碳质物典型拉曼光谱(据吴娟霞等，2014修改)；(d)碳质物各个拉曼特征峰产生过程(据吴娟霞等，2014)Fig.2 Formation principle of carbon material Raman spectroscopy(a) phonon dispersion relation in graphite (modified after Wu et al., 2014)；(b) vibration mode and frequency of graphite group (after He, 2005)；(c) example of Raman spectrum of carbon material (modified after Wu et al., 2014)；(d) generate process of carbon material Raman characteristic peak (after Wu et al., 2014)

图2d展示了碳质物典型拉曼特征峰产生的过程，G峰是与布里渊区中心双重简并的iTO和iLO光学声子相互作用的结果(Tuinstra and Koenig, 1970)。Tuinstra and Koenig(1970)最初估计G峰的位置约为1575cm-1，后人的研究也表明G峰的位置及强度随入射波长的变化而变化(Wangetal., 1990；Matthewsetal., 1999；Satoetal., 2006)。D1峰最初归因于碳质物小晶体或大晶体边缘的A1g振动模式(Tuinstra and Koenig, 1970)，但进一步的研究发现D1峰是一个iTO声子与一个缺陷谷间散射的结果(Beny-Bassez and Rouzaud, 1985；Malardetal., 2009；吴娟霞等，2014)。D2峰则为谷内双共振过程，两次散射过程分别为与缺陷的谷内散射和与K点附近的iLO声子的非弹性谷内散射过程(吴娟霞等，2014)，常出现在G峰段肩部，在结晶度低的碳质物中，常不能将二者分开，只在1600cm-1附近现一个宽带(Kouketsuetal.(2014)称其为Gl带)。D3峰推测来自无定形碳(Sadezkyetal., 2005)，Beny-Bassez and Rouzaud(1985)将该带归因于四面体碳等面外缺陷，认为这种缺陷在石墨化过程早期出现。D4峰由sp2-sp3键或多烯类结构的C-C和C=C伸缩振动产生。S1峰是与K点附近的iTO光学声子发生两次谷间非弹性散射产生的，S1峰拉曼位移约为D1峰的两倍，因此通常表示为2D峰，但S1峰的产生与缺陷无关，并非D1峰的倍频信号(吴娟霞等，2014)。在石墨化的最终阶段S1峰将会分裂成两部分，这种分裂被解释为碳质物二维结构朝向三维结构过渡的结果(Lespadeetal., 1984)。至于S2峰，它的含义还不是很清楚，通常只出现在结晶度低的碳质物中，Tsuetal.(1978)将其归因于C-H键的存在，但是这种假设仍存在争议。

如上所述，产生D峰的缺陷种类很多，如结构缺陷、面内杂原子等。最初Tuinstra and Koenig(1970)根据D峰强度与晶体尺寸的关系，并给出著名的TK(Tuinstra Koenig)公式：

ID/IG=C(vL)/La

(i)

该公式首次建立了碳质物石墨化程度与拉曼光谱的关系。式中ID/IG是D峰和G峰的强度比，La是纳米晶体的横向尺寸(平行于石墨烯平面)。考虑到D峰可由其他类型的缺陷所激活(如局部杂质)，新近研究量化了ID对离子轰击在石墨上引起的缺陷密度的依赖性(Ferreiraetal., 2010；Luccheseetal., 2010)。在这种情况下，TK关系变成了(ID/IG)∝(1/La2)，其La2是石墨烯平面中缺陷的平均距离。已知随着石墨化程度(结晶度)的增加，La逐渐增大，因此可以通过ID/IG来量化表示碳质物的石墨化程度(结晶度)(Wopenka and Pasteris, 1993；Beyssacetal., 2002b)。

变质沉积岩中碳质物拉曼光谱表现出随变质等级系统变化(图3)，通常变质等级越高，拉曼光谱谱峰值的数量越少(Pasteris and Wopenka, 1991；Wopenka and Pasteris, 1993；Yuietal., 1996；Beyssacetal., 2002a)，并且实验和天然样品观测表明，碳质物质的石墨化过程中温度是主要控制因素，而压力为次级影响因素(图4a, b)(Landis, 1971；Wopenka and Pasteris, 1993；Wadaetal., 1994；Beyssacetal., 2002a, b；Rahletal., 2005；Aoyaetal., 2010；Lahfidetal., 2010；Kouketsuetal., 2014)。对天然地质样品观测显示，随变质程度的增加，La(石墨结晶度参数)随之增加，即石墨化程度增加(图4c)(Wopenka and Pasteris, 1993)。在此基础上Beyssacetal.(2002a)根据拉曼参数R2(R2=D1/(G+D1+D2)area)与变质温度之间的正相关性，拟合出碳质物拉曼参数与变质温度之间的关系方程，建立了碳质物温度公式(如图4d)。

1.2 碳质物拉曼光谱温度计公式

Beyssacetal.(2002a)通过激光拉曼(514.5nm入射激光)分析了全球10个区域变质地区的54个样品，发现碳质物结晶度与变质峰期温度密切相关，而与变质压力无关。基于变质矿物组合获得的变质温度和R2参数之间的线性关系，构建了温度计算公式(公式1，表1)。

表1变质岩中碳质物拉曼温度计公式

Table 1 Various formulas for carbon material Raman thermometers

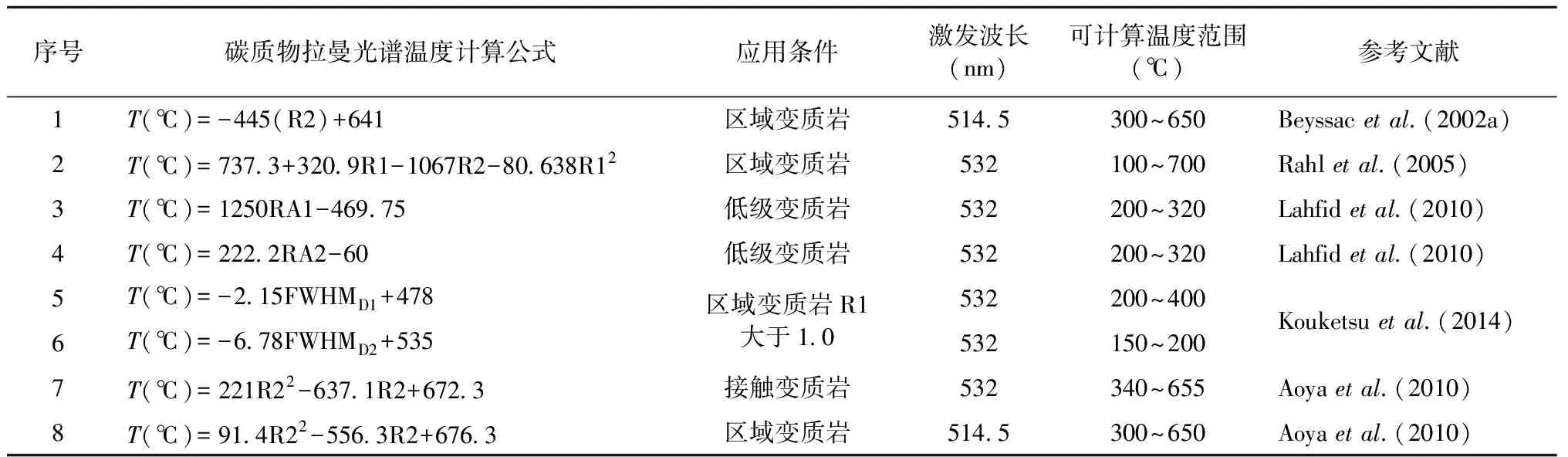
序号碳质物拉曼光谱温度计算公式应用条件激发波长(nm)可计算温度范围(℃)参考文献1T(℃)=-445(R2)+641区域变质岩514.5300～650Beyssac et al.(2002a)2T(℃)=737.3+320.9R1-1067R2-80.638R12区域变质岩532100～700Rahl et al.(2005)3T(℃)=1250RA1-469.75低级变质岩532200～320Lahfid et al.(2010)4T(℃)=222.2RA2-60低级变质岩532200～320Lahfid et al.(2010)56T(℃)=-2.15FWHMD1+478T(℃)=-6.78FWHMD2+535区域变质岩R1大于1.0532532200～400150～200Kouketsu et al.(2014)7T(℃)=221R22-637.1R2+672.3接触变质岩532340～655Aoya et al.(2010)8T(℃)=91.4R22-556.3R2+676.3区域变质岩514.5300～650Aoya et al.(2010)

注：R1=D1/Gintensity；R2=D1/(G+D1+D2)area；RA1=(D1+D4)/(D1+D2+D3+D4+G)area；RA2=(D1+D4)/(D1+D2+D3+D4+G)area；FWHMD1和FWHMD2分别是D1峰和D2峰的全峰半高宽

图3 变质岩中碳质物拉曼光谱随温度增加演化图数据来源: Beyssac et al., 2002b；Lahfid et al., 2010Fig.3 The evolution of Raman spectra of carbon material with increasing metamorphic temperature in metamorphic rockAll the samples come from Beyssac et al., 2002b；Lahfid et al., 2010

该温度计适用于区域变质岩，基于碳质物石墨化过程不可逆性(Landis, 1971；Pasteris and Wopenka, 1991；Wopenka and Pasteris, 1993；Wadaetal., 1994；Buseck and Beyssac, 2014)，Beyssacetal.(2002a)解释该温度代表变质峰期温度。

为了将碳质物拉曼温度计外延至更低的温度，Rahletal.(2005)通过激光拉曼(532nm激光源)对来自华盛顿州奥林匹克山脉的11个经历变质的硅质碎屑岩样品进行分析，拉曼数据结果显示，R1(R1=D1/Gintensity)在低温变质过程中(100～350℃)仍然保持变化，从115℃的0.5增加到250℃的2.1，随后在更高的温度条件下减小，这些学者们结合Beyssacetal.(2002a)的数据，提出新的经验性温度估算方程，将碳质物拉曼温度计的应用范围扩展至100～700℃(公式2，表1)。

Rahletal.(2005)对该公式进行了方差和残差的检验，得出该公式在95%的置信度的情况下误差为±50℃。但其也强调该公式仅仅是对已有数据拟合得到的一个经验公式，还需要在实际的地质运用中进行修正和完善。

图4 碳质物石墨化程度与温度、压力之间的关系(a)碳质物石墨化程度与变质温度之间的关系(据Wada et al., 1994)；(b)温度和压力对碳质物石墨化程度的影响(据Landis, 1971)；(c)变质等级与碳质物石墨化程度之间的关系(据Wopenka and Pasteris, 1993)；(d)碳质物拉曼光谱参数(R2)与变质温度之间的关系(据Beyssac et al., 2002a)Fig.4 The relationships between the degrees of graphitization of carbon material and temperatures/pressures(a)relationship between the degrees of graphitization and the metamorphic temperatures(after Wada et al., 1994)；(b)effect of temperatures and pressures on the degrees of graphitization(after Landis, 1971)；(c)the relationship between metamorphic grades and degrees of graphitization of carbon material(after Wopenka and Pasteris, 1993)；(d)the relationship between the Raman parameter(R2)and the peak metamorphic temperature(after Beyssac et al., 2002a)

Lahfidetal.(2010)对格拉鲁斯阿尔卑斯山低级变质岩(钙质片岩、石英片岩)的研究发现，低级变质岩中的碳质物拉曼光谱与高级变质岩中碳质物拉曼光谱明显不同且更加复杂，最显著的区别是高等级变质岩碳质物拉曼光谱中不存在D3、D4峰。低级变质岩中碳质物拉曼光谱的复杂性也暗示Beyssacetal.(2002a)基于中级变质程度提出的温度计不能简单的扩展至低温环境。进而，Lahfidetal.(2010)通过比较各种参数(如R1、R2)描述碳质物拉曼光谱随变质等级增加演变的能力，提出了两个新的参数RA1(RA1=(D1+D4)/(D1+D2+D3+D4+G)area)和RA2(RA2=(D1+D4)/(D1+D2+D3+D4+G)area)，用于定量化描述格拉鲁斯阿尔卑斯山低级变质岩(钙质片岩、石英片岩)在200～320℃范围内的碳质物拉曼光谱随温度演化(图5)，通过简单变换可得到应用于200～320℃范围内的温度计方程式(公式3、4，表1)。该温度计误差为±25℃，然而该温度计仅由一个变质区域的样品构建，正如Lahfidetal.(2010)所阐述的，用于校准该温度计的样品变质温度在一个有限的范围内，因此，无法将该温度计外延到温度高于320℃的变质环境。

近年来，Kouketsuetal.(2014)利用激光拉曼(532nm入射激光)对日本中央构造带内的19个变质沉积岩中碳质物进行分析，将获得拉曼光谱参数(R1、R2等)与样品已知的变质温度进行比较，发现变质温度与D1峰和D2峰的全峰半高宽(FWHMD1、FWHMD2)呈负相关，并利用二者之间的相关性，构建了适用于150～400℃温度范围的地质温度计，即半宽高(FWHMD1、FWHMD2)与变质温度的关系方程(公式5、6，表1)。

Kouketsuetal.(2014)认为，在200～400℃的变质条件下，公式5比公式6更为准确，而在150～200℃的变质条件下，公式5更准确，公式5的误差为±30℃，而公式6的误差为±50℃(在FWHM柱状图不出现宽峰或者双峰的条件下)。当变质温度接近或者超过400℃时使用该公式需要谨慎，Kouketsuetal.(2014)提出了在此情况下使用该温度计的条件，当D1/G(强度)大于1.0时，公式5、6是适用的，当D1/G(强度)小于1.0时，使用公式5或6时应当与前人提出的温度计进行相互检验和验证。值得注意的是，前人提出的温度计均是以比率作为参数，这样做的好处是可以减少对实验设备的依赖性，但Kouketsuetal.(2014)通过比较不同实验室的测量结果，认为FWHM测定不受实验室变化的影响。此外由于该温度计使用的温度范围为150～400℃，贯穿了碳质物从无定形碳向结晶石墨转化的整个过程，因此在选择拉曼谱峰拟合方法时尤需严谨以便获得可靠的温度，拉曼谱峰分解方法可参考Kouketsuetal.(2014)提出的谱峰拟合程序。

Aoyaetal.(2010)将温度计适用范围从区域变质岩扩展至接触变质岩。接触变质岩与区域变质岩最大的不同是岩石变形弱且加热时间长，这种属性导致接触变质岩中碳质物结晶程度高，表现为更低的R2值(Aoyaetal., 2010)，由于使用532nm激光比使用514.5nm激光能够获得相对更大的R2值(Wangetal., 1990；Matthewsetal., 1999；Satoetal., 2006；Beyssac and Lazzeri, 2012)，因此Aoyaetal.(2010)使用532nm激光拉曼对来自日本Daimonji和Kasuga地区的领家变质带中的11个接触变质岩样品(原岩为泥质岩和砂岩)进行分析，并提出适用于接触变质作用过程的温度估算的公式(公式7，表1)。

表2碳质物温度计的影响因素

Table 2 Affecting factors of the carbonaceous Raman spectroscopy thermometers

碳质物拉曼光谱温度计影响因素误差来源误差减小措施参考文献光谱拟合引入的误差碳质物自身特性引入的误差拉曼光谱系统使用时的误差基线校正、谱峰拟合函数的选择样品制备、样品的非均质性及碳质物结构各向异性入射激光波长及拉曼光谱获取时间基线校准中明确所有假设, 使用洛伦兹函数拟合谱图测量薄片内部碳质物,单个样品测量数大于50根据计算公式合理选择激光波长,垫块铜片导热或在 薄片中测量Lünsdorf et al.(2014)

图5 格拉鲁斯阿尔卑斯山地区低级变质岩内碳质物拉曼光谱参数随变质温度演化图(据Lahfid et al., 2010)(a)RA1随变质温度演化图；(b)RA2随变质温度演化图Fig.5 Evolution of carbon material Raman spectral parameters with metamorphic temperatures in low-grade metamorphic rocks in the Glarus Alps(after Lahfid et al., 2010)(a)evolution of the RA1 with temperature；(b)evolution of the RA2 with temperature

这些作者强调该温度计适用范围是340～655℃的接触变质岩，测试过程使用的入射激光波长为532nm。此外，Aoyaetal.(2010)发现Beyssacetal.(2002a)所提出的温度计在温度小于330℃及大于550℃时估算存在明显偏差。因此利用Beyssacetal.(2002a)报道的数据对区域变质岩的温度计进行了进一步修正(入射激光514.5nm)，如公式8(表1)。

修正后的温度计算公式，适用温度范围为300～650℃(Aoyaetal., 2010)，Aoyaetal.(2010)认为Beyssacetal.(2002a)提出的温度计不仅适用于区域变质岩，也适用于接触变质岩，只不过在接触变质岩温度估算中误差较大(±50℃)，但该温度计(公式7，表1)可通过增加测试点数量来降低温度估算误差(主张单个样品测量的数量应大于50个)，误差可降至±30℃。

1.3 碳质物拉曼光谱温度计的影响因素

碳质物拉曼光谱测试从样品制备到光谱处理过程中产生误差的原因可归结为三大类(表2)：(1)光谱的拟合引入的误差；(2)碳质物自身特性引入的误差；(3)拉曼光谱系统使用时的误差(Lünsdorfetal., 2014)。光谱拟合过程中的误差来自于不同的基线校正，用于峰匹配的不同数学函数以及不同的拉曼光谱模型。碳质物自身特性引入的误差主要来自碳质物结构的各向异性、样品的制备及样品的非均质性。拉曼光谱系统使用产生的误差主要与入射激光的波长及测量时间有关，下文将对这三类影响因素做进一步的阐释。

图6 碳质物拉曼光谱拟合实例(使用Voigt函数三波段拟合)Fig.6 Example of peak-fitting procedures for Raman spectroscopy of carbon material(three-bands fitting by using Voigt function)

图7 薄片表面碳质物与内部碳质物拉曼光谱对比(a)青藏高原嘉黎韧性走滑剪切带内的糜棱岩化片岩单偏光显微照片；(b)碳质物反射光及透射光下的显微照片；(c)表面及内部碳质物拉曼光谱Fig.7 Comparison of Raman spectra of carbon material obtained at the surface of a thin section(triangle)and at inside within the thin section(circle)(a)photomicrograph under single polarized light for the mylonite schist from Jiali ductile strike-slip shear zone of the Tibet；(b)photomicrographs under reflected and transmitted light for carbon material from Fig.7a；(c)Raman spectroscopy of carbon material obtained at the surface of a thin section and at inside within the thin section

从拉曼光谱中获取碳质物结晶度定量参数需要进行光谱拟合，光谱拟合过程中用于峰匹配的数学函数以及不同的拉曼光谱模型的选择受个人影响较大，建立一种可靠且重复的碳质物拉曼光谱拟合的方法是开发适用于各种变质温度的碳质物拉曼温度计需要克服的最大问题之一(Kouketsuetal., 2014)。目前，光谱拟合普遍使用Peakfiting和Fityk软件，通常不同的光谱拟合软件对拟合结果不会产生影响(Lünsdorfetal., 2014)。光谱拟合第一步是基线校正，这对任何拟合程序的质量和可重复性都至关重要，对于石墨很简单，因为基线是线性的，如果结构很混乱，基线会变得很复杂，通常伴随着荧光性组分的影响，荧光可能是由相邻的矿物质导致的，基线校准过程中必须明确规定做出的所有假设。关于光谱拟合，使用最多的函数是Voigt(洛伦兹和高斯函数的组合)和洛伦兹函数。对于高结晶度的石墨，使用Voigt函数的三波段拟合(G、D1和D2)将产生优异的结果(图6；Beyssacetal., 2003, 2004)；随着碳质物结晶度的降低，在拉曼光谱一阶序区出现D3峰，对于低结晶度碳质物光谱，使用五个Voigt函数将会增加系统的自由度并导致多种拟合方案。另一种方法是使用纯洛伦兹或高斯函数来降低系统的自由度，以此获得唯一且可重复的拟合方案(Sadezkyetal., 2005；Lahfidetal., 2010)。Lünsdorfetal.(2014)认为对于低结晶度碳质物拉曼光谱只使用洛伦兹函数拟合将得到更好的结果，而随着碳质物结晶度的增加，拟合函数的选择不会影响拟合结果。由于洛伦兹函数拟合对低结晶样品和高结晶样品光谱拟合均表现良好，因此Lünsdorfetal.(2014)建议使用该函数拟合所有结晶度的样品。

碳质物自身固有的误差主要来源于样品的制备、样品的非均质性及碳质物结构的各向异性(Beyssac and Lazzeri, 2012；Lünsdorfetal., 2014)。Pasteris(1989)研究发现，除碳质物固有结构缺陷外，锯切或抛光可能产生新的结构缺陷，对薄片表面碳质物进行直接测试将会受新产生的结构缺陷影响。这些缺陷在拉曼光谱中无法区分，且随着碳质物的结晶度增加锯切或抛光产生的影响也增加，这种效应对于晶格完整的石墨最为显著(Beyssacetal., 2003)。Pasteris(1989)认为通过测量薄片内部的碳质物可避免这种误差，即将激光聚焦在透明/半透明相邻矿物颗粒下方的碳质物来实现。笔者的研究也从“反面”进一步证实了这种效应，如图7所示，图中表层碳质物其实并未真正的暴露在薄片上表面，相反，内部的碳质物已经暴露在薄片的下表面，受抛光的影响产生缺陷峰。因此将激光聚焦在透明/半透明相邻矿物颗粒下方的碳质物时，也应注意透明颗粒下方的碳质物是否暴露在岩石薄片的下表面。

除了薄片制备过程会产生误差外，碳质物取向(结构各向异性)相对于入射激光的方向，对拉曼光谱也有影响，尤其是结晶程度高的石墨(Katagirietal., 1988；Wangetal., 1989；Compagninietal., 1997)。通常入射激光垂直于C轴比平行C轴产生的G峰更小，D1峰更大，即R2值在垂直于C轴的测量中较大(Aoyaetal., 2010；Beyssac and Lazzeri, 2012)。Aoyaetal.(2010)比较了入射激光平行和垂直于C轴的测量结果，以检验取向的影响，结果表明对于结晶度高的碳质物，平均R2比率不受取向的影响，但R2非零值，在垂直于C轴和平行于C轴方向上存在很大的差异，入射激光垂直于C轴会比平行于C轴产生更大的R2值，但只要测量的数量足够多(N≥25)，即使是结晶度高的碳质物，R2的平均值也不受碳质物取向的影响。上述的讨论表明，结晶度高的碳质物R2取向效应更为显著，这是由于结晶度高的石墨具有较强的各向异性(Beyssacetal., 2002a)。

相比碳质物的非均质性，碳质物取向的影响可以忽略(Aoyaetal., 2010)。天然碳质物结构和化学成分在微米尺度上通常是不均匀的(Planeixetal., 1994；Dreyer and Bielawski, 2011)。很多学者通过透射电镜(TEM)和X射线吸收近边光谱(XANES)在纳米尺度上对碳质物的非均质性进行了观测(Buseck and Huang, 1985；Beyssacetal., 2002b；Bernardetal., 2007, 2008；van Zuilenetal., 2012)，结果表明碳质物结构非均质性非常强，结晶度高的石墨和结晶度低的无定型碳共存于同一块岩石中。如陨石中Fe-Ni颗粒中包含石墨片，而陨石基质中则存在低结晶度无定型碳(Pianietal., 2012)，以及变质沉积岩中由有机物石墨化产生的碎屑石墨和无定型碳共存(Beyssacetal., 2004)。在这两种情况下，石墨和无定型碳不是同时形成的，但却经历相同的石墨化过程。因此，在拉曼研究过程中，对碳质物进行岩石学研究以描述其形态和与矿物的结构共生关系至关重要。Aoyaetal.(2010)通过实验表明这种来自于碳质物非均质性的误差可以通过大量的测试数据(单个样品测量数N>50)来减小。

拉曼系统固有误差可能来自于拉曼光谱的获取时间及入射波长的大小。由于黑色的碳质物会吸收可见光范围内的光(激光)，不同的拉曼光谱获取时间即不同的加热时间，碳质物受热会导致光氧化或局部燃烧，从而改变局部化学成分和结构(Beyssac and Lazzeri, 2012)。激光诱导的加热是G峰、D峰左移的原因(Everalletal., 1991；Kagietal., 1994)。Tuinstra and Koenig(1970)测得G峰位置为1575cm-1可能是由于这种原因造成的(现在普遍接受的是1580cm-1)。对于从岩石中提取出的碳质物，激光加热效应尤为显著，解决方法是在提取出的碳质物下方垫块铜片并置于氩气环境中(Beyssac and Lazzeri, 2012)。对于薄片样品，激光加热引起的误差可以忽略(Aoyaetal., 2010)。这是由于薄片中碳质物不会直接暴露在空气中，并且诱导产生的热量也可以通过上方或周围的矿物传导散去。

此外，入射激光的能量对碳质物拉曼光谱具有显著的影响，尤其是缺陷峰(D峰)，通常入射激光能量的减小会使D峰向左偏移(Satoetal., 2006)。碳质物拉曼光谱常用的入射激光能量为2.33eV(532nm)，地球科学领域常用的激光能量为2.41eV(514nm)，但由于在低等级(低温)变质岩中，更高的激光能量能够减少荧光背景并获得较大的R1、R2比值，因此近年来所提出的温度计多使用2.33eV(532nm)的入射激光来获取拉曼图像(Aoyaetal., 2010；Kouketsuetal., 2014)。

2 碳质物拉曼光谱温度计与传统温度计对比

图8 碳质物温度计与传统温度计估算结果对比Fig.8 Comparison of calculated results from the carbon material thermometer and traditional thermometers

上述不同学者所提出的温度计已被应用于不同的变质岩区，特别是Beyssacetal.(2002a)提出的基于R2构建的温度计应用最为广泛。为评估碳质物拉曼温度计可靠性，本次研究对已发表的同一地区同一地体碳质物拉曼温度计所估算的温度与传统温度计计算的温度进行了对比，包括尼泊尔低喜马拉雅泥质片岩(Beyssacetal., 2004)，尼泊尔DZAKAACHU地区的藏南拆离系中的糜棱岩化大理岩(Cottleetal., 2011)，印度阿鲁纳恰尔地区喜马拉雅造山带中的长英质片岩、云母片岩、千枚岩(Mathewetal., 2013)，龙门山片岩(Robertetal., 2010)，西阿尔卑斯Oisans地块的灰岩、页岩及绿泥石片岩(Bellangeretal., 2015)，新西兰奥塔哥片岩(Huetal., 2015)，西摩洛哥Jebilet地块绿片岩、角闪岩相变质的泥质岩(Delchinietal., 2016)，日本西纪伊半岛泥质片岩(Yoshidaetal., 2016)，希腊基克拉泽斯蓝片岩和榴辉岩(Laurentetal., 2018)(表3)。

对比结果如图8所示，图中横坐标为碳质物拉曼温度计(基于Beyssacetal.(2002a)和Rahletal.(2005)温度计公式)估算的峰期变质温度，纵坐标为传统温度计(相平衡模拟、矿物组合)获取的变质温度，虚线为y=x直线。结果显示碳质物拉曼温度计与传统温度计所获得的变质温度值均分布于y=x斜直线附近，总体上碳质物拉曼温度计与传统温度计估算的温度较为接近，二者之间的差别也在分析和校准误差范围内。拉曼温度计相对误差通常小于15℃，远小于传统温度计(±50℃)。但Robertetal.(2010)和Cottleetal.(2011)在龙门山、尼泊尔DZAKAA CHU地区的研究表明，碳质物拉曼温度计与传统温度计存在较大差异，二者结果相差约100℃，原因是Cottleetal.(2011)和Robertetal.(2010)用传统温度计估算的温度代表退变质温度，而碳质物拉曼温度计结果为峰期变质温度，且不受后期退变质的影响(Landis, 1971；Pasteris and Wopenka, 1991；Wopenka and Pasteris, 1993；Wadaetal., 1994；Beyssacetal., 2002a, b, 2004, 2007；Rahletal., 2005；Negroetal., 2006；Angiboustetal., 2009；Gabaldaetal., 2009；Lahfidetal., 2010)，因此，二者之间存在较大差异。

3 碳质物拉曼光谱温度计在地学中的应用

解析造山带形成过程的空间和时间热演化是造山带研究的核心。变质温度估算、热年代学和地质年代学已成为约束造山带热演化的关键信息。传统温度计对于特定矿物组合的要求限制了其在造山带中的应用，而每个造山带均会产生增生楔沉积物质，这些沉积单元中富含碳质物，为碳质物拉曼温度计的使用提供了基本的物质基础。 碳质物拉曼光谱温度计一经提出便得到广泛使用，如在造山带热结构和热演化史方面(Beyssacetal., 2004；Robertetal., 2010；Cottleetal., 2011；Kellett and Grujic, 2012；Cooperetal., 2013； Mathewetal., 2013；Scharfetal., 2013；Bellangeretal., 2015；Boutouxetal., 2016；Delchinietal., 2016；Yoshidaetal., 2016；Laurentetal., 2018；Mollietal., 2018)、成矿流体的古流体热异常(Clercetal., 2015；Delchinietal., 2017)、以及强应变带剪切热过程等(Furuichietal., 2015；Morietal., 2015；Itoetal., 2017)。在实际运用的过程中，其有效性也得到了进一步的检验(Beyssacetal., 2004；Scharfetal., 2013；Delchinietal., 2016；Laurentetal., 2018)。

表3碳质物温度计与传统温度计对比表

Table 3 Calculated results from carbon material geothermometers and conventional geothermometers

地区碳物质拉曼温度计传统温度计温度(℃)标准误差(℃)温度(℃)系统误差(℃)碳物质拉曼温度计公式传统温度计方法参考文献尼泊尔低喜马拉雅541.716.1558.820.4Beyssac et al.(2002a)石榴石-云母Fe2+-Mg交换温度计(最高变质温度)Kohn et al. (2001)、Beyssac et al. (2004)尼泊尔DZAKAA CHU地区藏南拆离系338.0479.0493.0545.0533.0544.0530.04.06.05.05.06.04.07.0350.0380.0365.0430.0430.0450.0550.050.040.040.020.020.040.030.0Beyssac et al.(2002a)多平衡矿物组合温压计,石英、长石微观结构(退变质温度)Cottle et al. (2011)印度阿鲁纳恰尔喜马拉雅造山带659.0681.8650.2669.3598.2422.6607.5617.0603.2610.2564.2413.47.87.38.510.913.412.33.32.33.84.59.66.7685.0677.0594.0603.0552.0458.0685.0677.0594.0603.0552.0458.055.035.058.070.045.011.055.035.058.070.045.011.0Rahl et al.(2005)Beyssac et al.(2002a)石榴石-云母Fe2+-Mg交换温度计(最高变质温度)Goswami et al.(2009)、 Mathew et al. (2013)龙门山599.0562.0515.0504.0547.010.010.010.010.010.0490.0480.0470.0417.0428.040.070.056.025.036.0Beyssac et al.(2002a)石榴石-云母Fe2+-Mg交换温度计、多平衡矿物组合温压计(退变质温度)Huang et al.(2003a,b)、de Sigoyer et al.(2008)、 Robert et al. (2010)西阿尔卑斯Oisans地块306.0345.0335.0308.0306.0345.0335.0308.013.09.05.05.013.09.05.05.0294.0296.0297.0288.0252.0313.0294.0269.017.09.012.013.061.055.045.051.0Beyssac et al.(2002a)石榴石-云母Fe2+-Mg交换温度计、绿泥石温度计(最高变质温度)Bellanger et al. (2015)新西兰奥塔哥239.0304.0226.0283.0433.0339.08.012.08.012.0200.0300.0200.0400.0400.0400.050.050.050.050.050.050.0Beyssac et al.(2002a)矿物组合(最高变质温度)Mortimer. (2000)、Hu et al. (2015)西摩洛哥Jebilet地块618.0613.0616.014.012.011.0620.0620.0625.012.012.025.0Beyssac et al.(2002a)基于相图计算的温压计(最高变质温度)Delchini et al. (2016)日本西纪伊半岛285.0289.07.013.0275.0270.025.030.0Beyssac et al.(2002a)矿物组合(最高变质温度)Yoshida et al. (2016)、Banno and Sakai (1989)希腊基克拉泽斯536.124.5530.030.0Beyssac et al.(2002a)石榴石-云母Fe2+-Mg交换温度计、基于相图计算的温压计(最高变质温度)Laurent et al. (2018)

Beyssacetal.(2004)利用该温度计限定了低喜马拉雅热演化，研究表明低喜马拉雅(LH)经历了一次大规模的热变质作用，温度从顶部540℃逐渐降低到最深折返层内的330℃。Mathewetal.(2013)利用Beyssacetal.(2002a)和Rahletal.(2005)提出的温度计估算了西阿鲁纳恰尔拉邦低喜马拉雅和西瓦里克热演化史，研究发现大喜马拉雅序列(GHS)在主中央逆冲区温度从700～800℃降至650～700℃，并在西瓦里克的中上新世序列中进一步降低至200℃，据此预测GHS倒置的变质梯度演化与渠道流模型紧密相关。在阿尔卑斯造山带，Bellangeretal.(2015)使用碳质物拉曼光谱温度计、绿泥石温度计结合白云母40Ar/39Ar原位测年对西阿尔卑斯Oisans地块的演化进行了温度和年龄的限制，提出了西阿尔卑斯外部结晶块(ECM)新的缩短模式。其后有学者结合锆石的(U-Th-Sm)/He与碳质物拉曼温度计数据，约束了西阿尔卑斯山ECM的热演化和折返过程(Boutouxetal., 2016)。Mollietal.(2018)将碳质物拉曼光谱温度计应用于亚平宁山脉，其搜集的数据修正了亚平宁山脉热结构及阿普亚内山核部变形与变质结构之间的关系，解释认为残存的古热结构及部分折返与地壳增厚有关，提出阿普亚内杂岩为冷的变质核杂岩。Laurentetal.(2018)利用石榴石平衡模型、P-T相图结合碳质物拉曼光谱测温数据恢复了希腊基克拉迪蓝片岩(CBU，Greece)峰期变质温度，表明该地区经历了多阶段的折返过程，并认为这种折返由板块回卷驱动制约。碳质物拉曼光谱温度计还被成功运用在洋壳深俯冲型低温-超高压变质杂岩带。通过碳质物拉曼光谱温度计和石英包裹体弹性压力计的联合应用，Bayetetal.(2018)对中亚造山带西端的西南天山低温-超高压变质杂岩带进行了区域大尺度的P-T绘图，发现前人所厘定的HP/UHP混杂岩的北部整体上经历了较为均一的低温超高压榴辉岩相峰期变质条件(2.5±0.2GPa，536±11℃)。此外，在对区域内前人工作进行了系统总结的前提下，Tanetal.(2019)基于激光微区40Ar/39Ar测年法、锆石U-Pb定年、相平衡P-T计算及碳质物拉曼光谱温度计等手段，开展了区域大尺度P-T-t-D绘图，指出前人所厘定的高压/超高压混杂带从北到南应划分为具有不同峰期变质P-T-t-D演化历史的四个次级构造单元，分别是：北部超高压单元(～2.75GPa，480～560℃，320±1Ma)，中部蓝片岩/榴辉岩相基性单元(～2.1GPa，505℃，332±2Ma)，中部低蓝片岩相超基性-基性单元(～1.45GPa，485℃，359±2Ma)及南部低蓝片岩-绿片岩相过渡带(>0.7～1.0GPa，470～520℃，ca. 280～310Ma)，所揭示出的四期短暂的深部岩石折返事件暗示了俯冲地温梯度存在时空上的渐进变化(～12℃/km到6～7℃/km)，这可能反映了俯冲带系统随着时间发生冷却。

许多矿床存在于富含碳质物的变质沉积物中。因此对碳质物结晶度的研究提供了估算岩石变质峰值温度的精确工具。地层温度通常由地层的埋藏剥蚀、岩浆侵入和流体循环控制。在热液矿床中，碳质物可以提供热事件及之后最高温的准确信息，因此，碳质物可以用于研究古温度并阐明流体流动引起的热异常(Clercetal., 2015；Delchinietal., 2017)。为了检验碳质物拉曼光谱温度计在热液矿床环境中检测热异常的能力，以美国加利福尼亚州的弗朗西斯卡杂岩Lucia微地体为例进行了研究，表明碳质物拉曼光谱温度计是确定由热液流动引起的热异常的可靠工具(Lahfidetal., 2010)。碳质物拉曼温度计在北比利牛斯Arguenos-Moncaup地区估算的变质温度也与前人研究结果吻合(Clercetal., 2015)，碳质物拉曼光谱温度数据集清楚地表明了地幔折返和热异常之间的联系，并且证实了该地区变质作用与白垩纪地壳减薄之间的联系。此外，碳质物拉曼光谱温度计提供了一个方便快捷获取岩石古温度的方法，并且能够广泛用于矿产勘查(Delchinietal., 2017)。Delchinietal.(2017)将碳质物拉曼光谱温度计运用至矿产勘探，通过碳质物拉曼温度计解析了Jebilet地块矿床的热历史，表明该地区经历了构造、变质和热液事件，这些因素共同影响着矿床的形成，同时也检验了碳质物拉曼光谱温度计对于检测古热异常的有效性。

图9 MTL地区热异常成因(据Mori et al., 2015修改)(a)垂直MTL断层的碳质物拉曼温度剖面；(b)MTL地区构造演化模型Fig.9 Causes of thermal anomalies in MTL areas(modified after Mori et al., 2015)(a)cross-sections across the MTL fault with carbon material Raman spectrum temperaturesand；(b)tectonic evolution model in MTL region

在大陆地壳发育长期活动的断层体系，如走滑断层，转换断层和俯冲边界。对主断层的剪切应力的估算是了解地壳强度和大地震的产生以及与运动相关剪切生热程度的重要前提。出露地表的断裂带记录了深部地壳的变形，是观测剪切生热和断裂强度的天然实验室。由于缺乏合适的矿物以及温度变化较小，基于传统岩相学的温度计不再适用(d’Alessioetal., 2003；Yamadaetal., 2007；Tagami, 2012)。Itoetal.(2017)通过分析天然和实验合成的粘土岩中假熔岩的拉曼光谱，认为假熔岩中的碳质物拉曼光谱特征可以用于评估共震断层强度。比较碳质物质结晶动力学实验的结果与热模拟结果表明，碳质物拉曼光谱温度计非常适合估算主断层带的剪切生热(Morietal., 2015)，这些作者对日本中央构造带(MTL)泥质片岩分析发现在垂直于MTL断层面的150m附近存在约60℃的峰值温度上升(图9a)，这种与断层空间相关联热异常意味它是由剪切加热引起的(图9b)。然而，近年来摩擦实验研究表明，镜质体反射率(R0)和碳质物拉曼光谱温度计均可以用于检测断层摩擦生热，但常规镜质体反射率(R0)和碳质物拉曼光谱温度计不能精准估算地震断层滑动期间的峰值温度，需要结合高位移速率下快速加热的反应动力学及碳质物原始微观结构和成分相关研究，建立适用于断层摩擦加热的碳质物拉曼光谱温度计(Furuichietal., 2015)。

4 结论

本文综述了碳质物拉曼温度计的基本原理和影响因素，对比分析了碳质物拉曼温度计与传统温度计估算结果，并讨论了该方法在造山带热结构恢复、热演化、以及断层剪切生热等方面的研究实例。

该方法是基于碳质物石墨化程度(结晶度)与温度之间的关系构建的温度计，其计算公式是通过分析大量天然与实验样品统计归纳得到的经验性公式，估算的温度代表峰期变质温度，不受后期退变质的影响，可估算的温度范围为100～700℃(相对误差±15℃，绝对误差±30℃)，与传统温度计相比更为便捷。

对于本文总结归纳的不同版本的碳质物拉曼光谱温度计，在使用的过程中我们需要根据研究区的地质条件和环境给予选择不同的温度计公式，就目前碳质物拉曼光谱温度计使用情况来看，普遍使用的是Beyssacetal.(2002a)提出的温度计及Rahletal.(2005)提出的温度计，但需要特别注意的是，Beyssacetal.(2002a)和Rahletal.(2005)提出的温度计适用于区域变质岩，当样品来自于接触变质带时，选择Aoyaetal.(2010)提出的温度计估算温度可能会得到更加准确的结果。

碳质物拉曼光谱温度计相比传统温度计其最大的特点是记录最高温变质温度，不受后期退变质影响，因此结合传统温压计可以更好的描述岩石多期次变质历史。但同时也需注意，影响碳质物结晶度的因素不仅仅只有温度，在低温环境中，压力、变质作用持续时间、碳质物前体类型甚至是变形均会影响碳质物结晶度，但目前为止，尚未有人量化这些因素对碳质物拉曼光谱温度计的影响，这也是碳质物拉曼光谱温度计今后需要进一步完善的地方。

致谢本研究成果还得到北京大学造山带与地壳演化教育部重点实验室SEM-EBSD实验室和TIMA实验室的资助；审稿专家及俞良军老师严谨细致审阅全文，提出了很多建设性的修改意见与建议，对论文质量的提高大有帮助；在此一并表示衷心感谢。