在线参数辨识和扩展卡尔曼算法的锂离子电池SOC估算研究

李博文，王顺利，于春梅，李建超，谢 伟

(1.西南科技大学信息工程学院，四川 绵阳 621010； 2.绵阳市产品质量监督检验所(国家电器安全质量监督检验中心)，四川 绵阳 621000； 3.四川华泰电气股份有限公司，四川 遂宁 629000)

0 引言

能源安全和环境保护在国家的发展规划中具有重要的地位。寻求可循环、低污染的新能源代替传统的化石燃料，已经成为各国关注的焦点[1]。锂离子电池以其能量密度高、使用寿命长和输出功率大等优点，已经在新能源领域获得长足的发展，受到人们的广泛关注[2]。锂离子电池作为能量的载体，其状态的实时监测越来越受到重视。能否准确估计锂离子电池荷电状态(state of charge,SOC)决定了电池性能能否充分使用[3]。荷电状态的准确估计很大程度上取决于根据电池工作特性建立的等效模型。由于锂离子电池内部结构复杂，在复杂工况下使用常常表现出强烈的非线性，使得传统的等效模型难以完全表征锂离子电池的工作特性[4]。因此，针对锂离子电池工作特性建立的等效电路模型，采用合适的算法进行SOC估算，实现对锂离子电池的实时状态监测，对提高算法精度具有重要意义。

目前，常见的锂离子电池模型有电化学模型、神经网络模型和等效电路模型等[5]。而常用的SOC估算算法有卡尔曼滤波算法、粒子滤波法和神经网络算法等。考虑到锂离子电池在复杂动力工况下使用，其状态监测往往受到环境噪声的影响[6]。加之电池内部复杂的化学反应、工况下电流和温度多变，电池材料多次循环使用导致电池老化等问题，使得传统的算法难以得出实时可靠的荷电状态值[7]。近年来，由于研究的不断深入和技术的革新，针对锂离子电池的在线估计难和估计精度较低等问题，在传统的算法的基础上提出了新的改进方法[8-9]。本文针对影响荷电状态准确估计的等效模型的影响因素问题，根据锂离子电池的二阶RC等效模型，基于含有遗忘因子的递推最小二乘法(recursive least squares method with forgetting factor,FFRLS)算法和扩展卡尔曼(extended Kalman filter ,EKF)算法，对动态应力测试(dynamic stress test ,DST)工况下进行在线参数辨识和SOC估算，实现对电池的特性的准确、有效估计。

1 理论分析

1.1 等效模型及状态方程建立

SOC被定义为电池剩余电量与额定容量的比值。其通常用安时积分法表示：

(1)

式中：SOC0为电池初始状态的SOC值；Q为电池的额定容量；i(t)为电池瞬时脉冲电流大小；η为库伦效率；Δt为采样时间周期。

考虑到实际工程需要，在满足要求的情况下，锂离子电池的动态等效电路模型不应由复杂的电池模型来表征。为了提高参数识别的准确性，选择如图 1所示的二阶RC等效电路模型。该模型能够充分描述锂离子电池的充放电状态，有助于反映基于最小二乘法的参数识别精度。

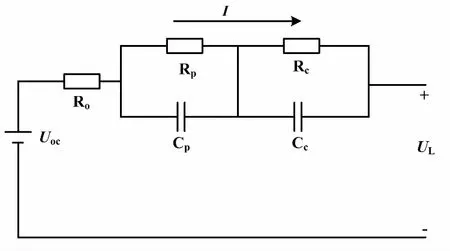
图1 二阶RC等效电路模型Fig.1 The second-order RC equivalent circuit model

图1中：UL为电池端电压；Uoc为电池的开路电压；Ro为电池的欧姆内阻；Rp为电池极化内阻；Cp为电池极化电容；Rc为电池浓差电阻；Cc为电池浓差电容。

当RC电路具有零输入响应时，通常认为两个RC电路的放电电流是相同的。通过锂离子电池模型获得的系统方程是连续时间模型，并且需要表征每个时刻的状态。每个t时刻的状态如式(2)所示。

(2)

式中:τc为极化效应时间常数；τp为浓差效应时间常数。

1.2 参数辨识

1.2.1 离线参数辨识

参数辨识的精度使得SOC估算受到影响。电池单次恒流脉冲循环充放电过程如图 2所示。

图2 单次恒流脉冲循环充放电图Fig.2 Schematic diagram of charge and discharge of single constant current pulse cycle

根据式(1)结合模型加以分析，当RC网络处于零输入状态时，可以获得电池状态表达式：

(3)

采用多线性拟合原理，结合实际工况数据用于分析电池的实时状态，能够实现对锂离子电池的离线参数辨识。

图2中：AB为放电区域；RC网络处于零响应状态；BD为搁置区域；RC网络处于零输入状态。

电压从B点突然上升，该突变是由欧姆内阻引起的[10]。根据锂离子电池特性结合等效电路模型分析，可以计算欧姆电阻Ro。

(4)

根据锂离子电池充放电下RC网络结合式(1)分析，在此基础上对试验放电数据拟合u(t)曲线进行多线性拟合分析，可以获得基于RC网络的零输入响应下Cc、Rc、Rp和Cp的参数值，如式(5)所示。

u(t)=uoc(soc)-up(t)-uc(t)=uoc(soc)-

(5)

1.2.2 最小二乘法原理

最小二乘法以其易于理解和快速收敛而被广泛应用于系统识别领域。基于最小二乘法的在线参数辨识可以根据实时采集到的电池信息更新电池模型参数，使得模型更加契合当前电池特性表示，从而有效提高模型精度。含有遗忘因子的递推最小二乘法算法原理如式(6)所示。

y(k)=φ(k)θ(k)T+e(k)

(6)

式中：φ(k)为观测向量；θ(k)为待估计参数向量；e(k)为观测噪声向量。

(7)

经典的最小二乘法随着算法数据的迭代次数变长，增益K(k)和矩阵方差P(k)变得越来越小。FFRLS算法增加遗忘因子(λ)来减弱之前迭代的影响，以提高算法的在线估计能力。算法的收敛速度和跟踪能力取决于遗忘因子(λ)的大小，如式(8)所示。

(8)

(9)

考虑到在二阶RC锂离子电池等效模型中，需要辨识的模型参数为Ro、Rp、Cp、Rc和Cc。根据最小二乘法原理并结合式(9),可以得出观测向量和待估参数向量分别为：

(10)

FFRLS算法实现如图3所示。

春到梅山处处香，秋临栖霞片片红。春入梅花山赏梅，夏临玄武湖观荷。泛舟玄武湖赏荷，漫步夫子庙观灯。夫子庙灯火齐放，玄武湖扁舟同行。夫子庙盏盏灯如昼，栖霞山片片枫似火。桃红柳绿莫愁湖，鸟语花香紫金山。梅花山踏雪寻梅观胜景，秦淮河泛舟赏月醉风光。望秦淮河水缠缠绵绵，观东郊园林郁郁葱葱。登明城墙赏金陵胜景，攀紫金山观石城风光。春雨蒙蒙百花争艳，秋风瑟瑟群菊盛开。

算法主要由上部的初始阶段和下部的更新阶段构成。通过预设初始值进行参数计算和相关矩阵的迭代更新，实现对工况下锂离子电池的在线参数辨识。本文经过反复计算验证，当遗忘因子为0.98时，系统参数辨识精度最高。

1.3 扩展卡尔曼原理

锂离子电池由于放电倍率、温度以及内部复杂的化学反应，呈现出非线性状态。EKF算法在卡尔曼算法的基础上运用泰勒式求取雅克比矩阵进行线性化处理，能够更加精确地实现SOC的估算[11]。通常基于EKF算法的锂离子电池等效模型表示为：

图3 FFRLS算法实现示意图Fig.3 FFRLS algorithm implementation diagram

(11)

式(2)中的Uoc可以由SOC表示。结合式(11)，针对所选取的二阶等效模型，选取[SOCk+1Up,k+1Uc,k+1]T作为状态变量，将等式离散化，可以列出其状态空间方程:

(12)

结合式(11)与式(12)进行分析，可以化简得到相关矩阵：

(13)

式中：Ak为状态转移矩阵；Bk为输入增益矩阵；Ck为量测转移矩阵；Dk为前馈系数矩阵。

对于上述状态空间模型表达式，运用卡尔曼滤波算法进行状态预测估计。其中，预测阶段状态估计值和协方差的递推关系式为：

(14)

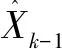
(15)

图4 EKF算法实现流程图Fig.4 Flowchart of EKF algorithm implementation

2 试验分析

2.1 参数辨识

本文选择中航锂离子电池进行试验,电池的标称容量为50 Ah，实际容量为48.54 Ah。在25 ℃下，对电池进行混合动力充放电(hybrid pulse power characterization,HPPC)试验，单次HPPC工步为以1 C(电流为50 A)恒流放电10 s、搁置40 s、以1 C(电流为50 A)恒流充电10 s、再搁置。将锂离子电池以1 C恒流放电6 min。在10个SOC的脉冲循环之间均间隔40 min。HPPC试验电压与电流变化曲线如图5所示。

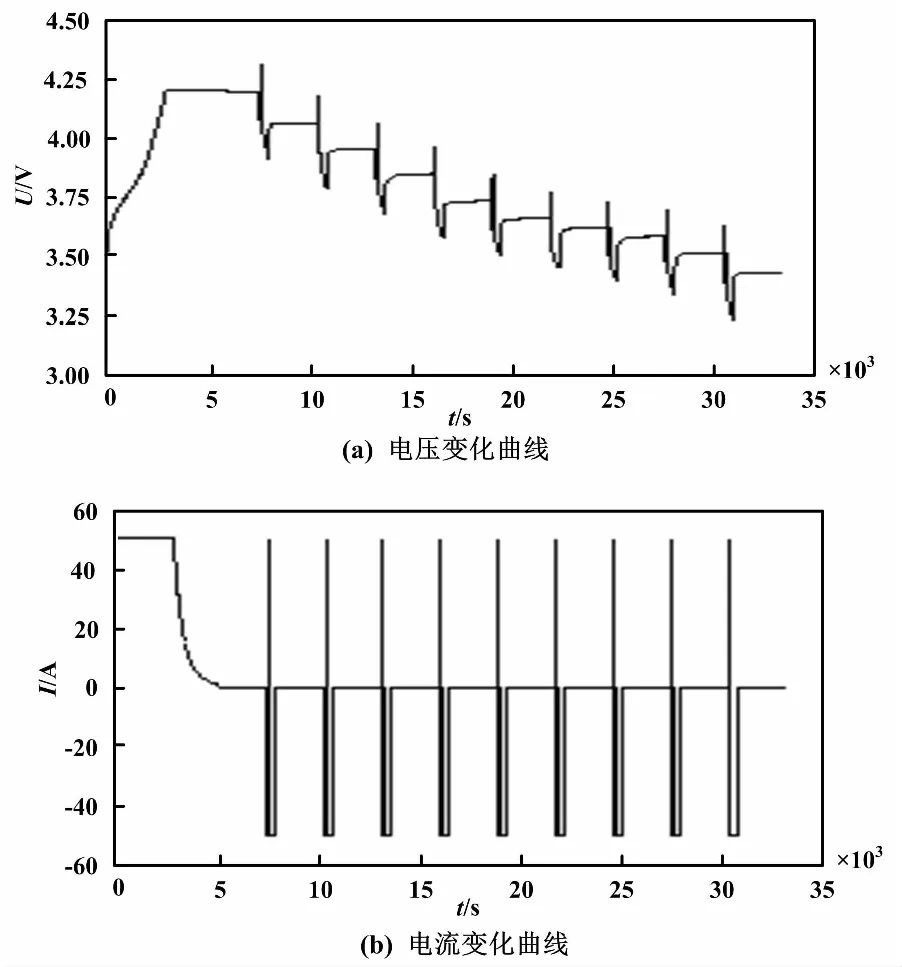
图5 HPPC试验电压与电流变化曲线Fig.5 HPPC experimental voltage and current change curves

根据对每个阶段的放电曲线进行分析，并结合式(4)运用多线性拟合法，实现对锂电池的等效模型的参数辨识。不同SOC状态下的模型参数如表1所示。

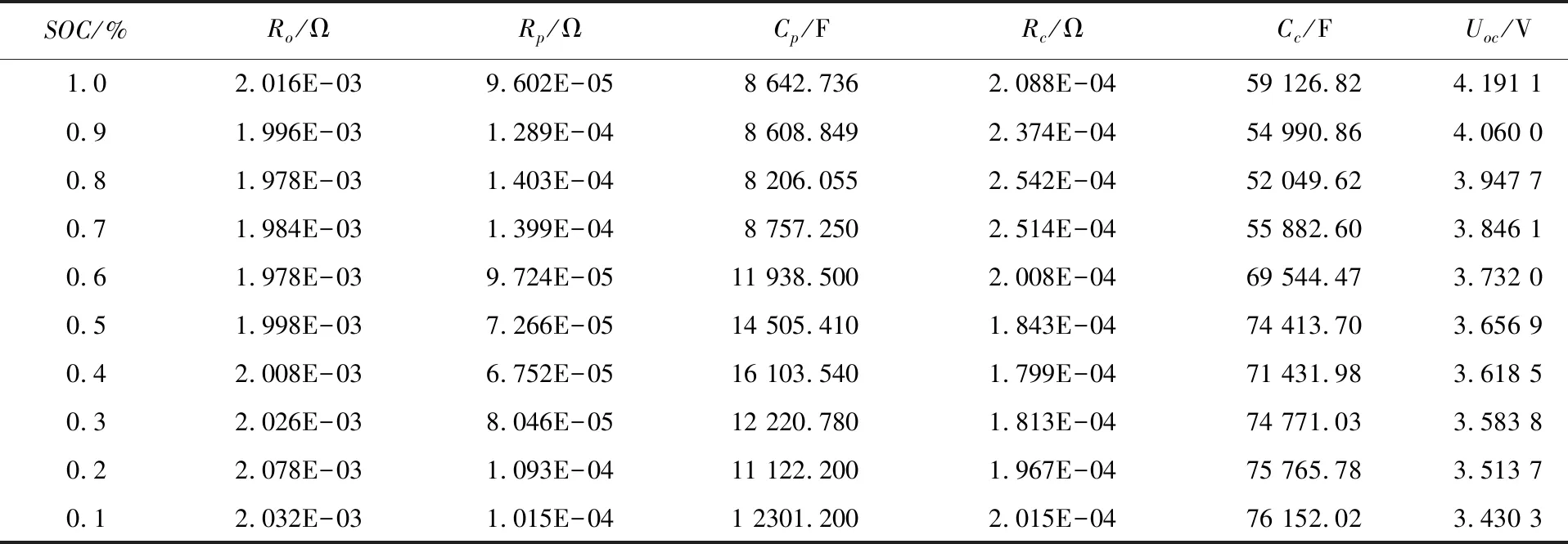
表1 不同SOC状态下的模型参数Tab.1 Model parameters under different SOC states

循环放电结束搁置后的电池基本处于稳定状态，此时的电压可以视为当前SOC所对应的开路电压(open circuit voltage,OCV)值。从表 1可以看出，二阶RC模型内部参数随着SOC变化在一定范围内波动，若需要得到较精确的模拟程度，则需要得到各参数和SOC之间的关系。

2.2 HPPC仿真分析

为了验证锂离子电池的参数辨识精度，引入HPPC实际工况电流和电压，构建基于安时积分法的SOC仿真电压的模型。选择相关离线辨识参数与SOC值的曲线关系来表征实际放电过程的电池内部特性变化。电压仿真误差曲线如图6所示。

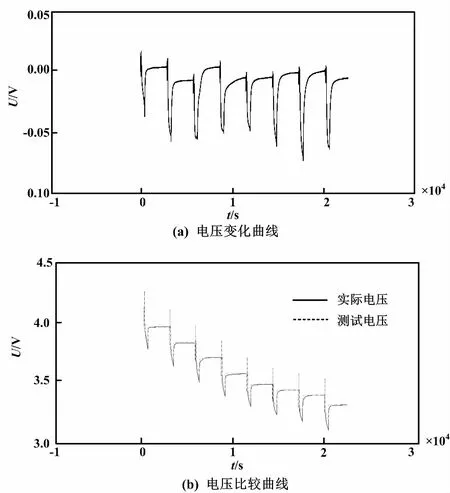
图6 电压仿真误差曲线Fig.6 Voltage simulation error curve

从图 6可以看出，实际电压和模拟电压变化曲线的误差基本稳定在0.05 V。仿真试验结果表明，通过参数识别得到的参数辨识值，能够用于表征实际工况条件下的锂离子电池工作特性。

2.3 动态应力测试仿真分析

为验证FFRLS算法对锂电池参数辨识在线估算的可行性，选择相同的中航三元锂电池为试验对象，根据实际的用户使用工作环境和要求，建立DST工况实验。工况条件下模拟用户以0.25 C、0.33 C、0.5 C进行断续的恒流放电工作，以0.25 C、0.33 C进行断续的恒流充电工作，并进行循环工作测试。动态应力测试(dynamic stress test,DST)试验电压与电流变化曲线如图7所示。

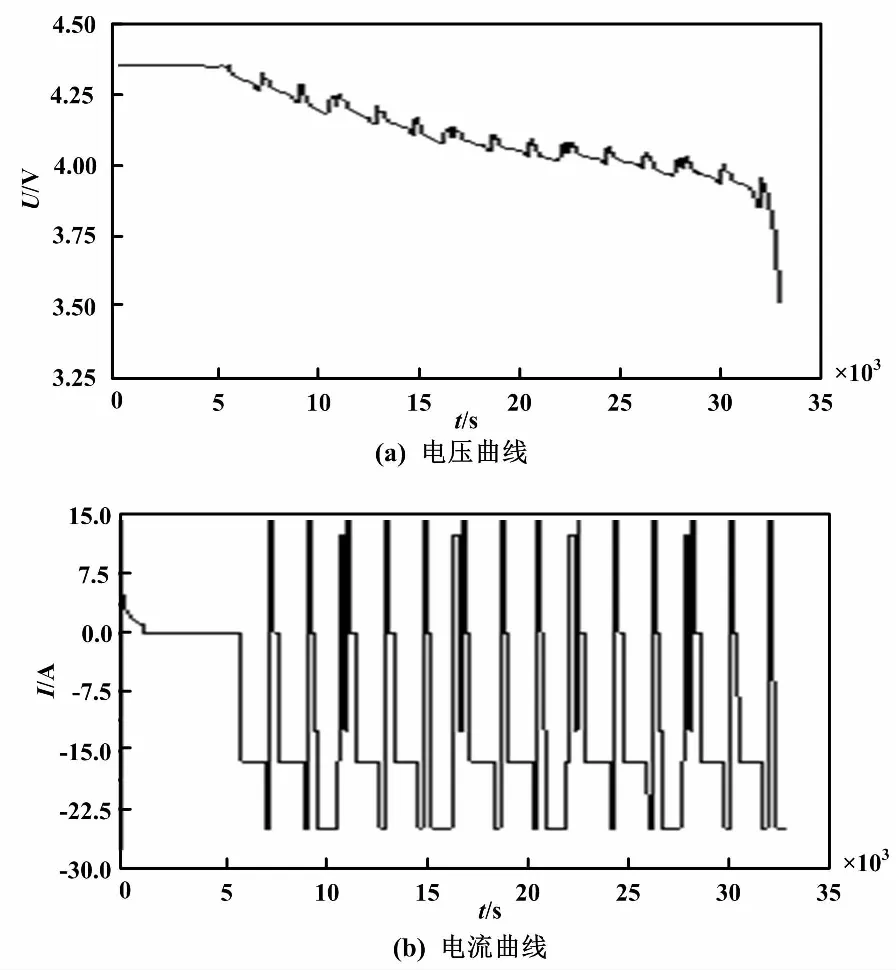
图7 DST试验电压与电流变化曲线Fig.7 DST experimental voltage and current change curves

根据FFRLS算法原理，结合DST工况试验数据进行锂离子电池等效模型的在线参数辨识。选择电压电流变化较为稳定可靠的前半段进行分析处理，获得仿真下的锂离子电池辨识参数。在线辨识参数变化曲线如图 8所示。

图8 在线辨识参数变化曲线Fig.8 Online identification parameter change curves

从图8可以得出，参数在线辨识与根据HPPC试验数据进行多线性原理分析获得的参数辨识数据相接近。结合式(1)进行分析，将在线辨识获取的影响因子在实际电流工作条件下表征电压。在线辨识参数电压仿真如图9所示。

从图9可以看出，基于FFRLS算法实现锂离子电池在线参数辨识获取的Ro、Rp、Cp、Rc和Cc的数值，能够仿真实际的电压情况，相对误差在2%以内。

为了验证利用FFRLS算法估计电池SOC的精度，在DST动态工况下，采用EKF算法结合FFRLS进行SOC估计，显示算法仿真模型估算SOC结果与实际值的对比情况。EKF估算SOC曲线如图10所示。由图10可知，DST工况下EKF算法对于实际SOC有较好的跟踪仿真能力，算法估算SOC的相对误差大约在0.3%。

图9 在线辨识参数电压仿真图Fig.9 Online parameter identification voltage simulation diagram

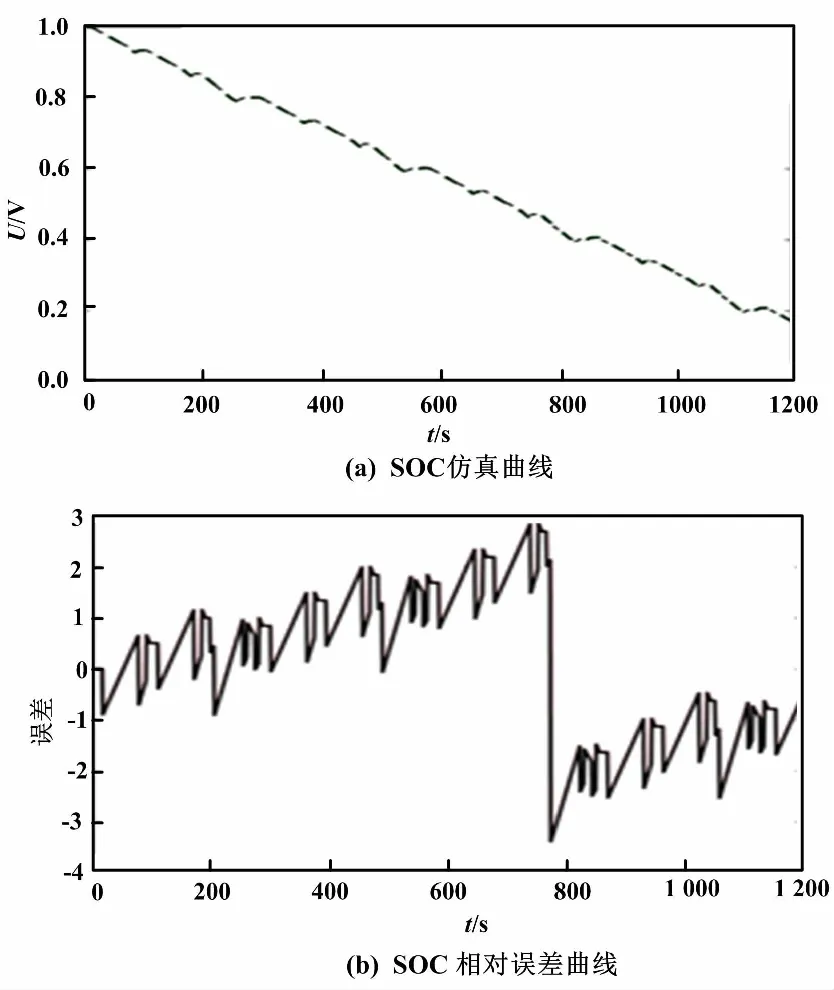
图10 EKF估算SOC曲线Fig.10 EKF algorithm to estimate SOC renderings

利用FFRLS在线参数辨识可以提高计算精度，但系统噪声与电池实际工况下存在的放电问题，使得图10(b)产生一定的误差波动。在线参数辨识下由于电池在工况条件下，相关参数会发生波动，如图8所示，会导致SOC估算精度出现较大误差。

3 结论

精确的SOC估计对于锂离子电池管理系统至关重要。模型参数和系统噪声等因素都会降低SOC的估算精度。本文提出基于FFRLS算法对二阶RC模型进行在线参数辨识来获取实时的电池参数，避免了由于参数拟合不精确引起的误差。运用DST工况试验采用EKF算法进行SOC估计。仿真结果表明，FFRLS能够正确表征锂离子电池在线参数辨识，与实际工况下相比较误差在1.5%以内。结合EKF算法能够有效表征SOC估算精度，相对误差在-0.3%～+0.3%以内。基于FFRLS算法和EKF算法的在线SOC辨识系统，具有较高的估计精度。