特高压交流输电线路电气不平衡度及换位研究

(中国电力工程顾问集团中南电力设计院有限公司，湖北 武汉 430071)

0 引 言

输电线路的不平衡度是衡量电力质量的重要参数，架空输电线路在线路正常运行时，各相导线都具有不同的线路参数，比如导纳、阻抗。这种参数上的不对等引起了输电线路中电流和电压的不对称，通常用电压、电流的不平衡度来衡量。当系统不平衡度超过限值时，回路中连接的电气设备就会受到影响，甚至影响线路正常运行[1]。

输电线路中，不平衡度的大小主要取决于导线相间的耦合程度，即导线电压、导线电流的负序、零序、正序分量之间的耦合程度。这个耦合程度与导线的空间相对方位有着直接的关系。进行导线不同相之间的换位，改变相间的空间相对方位，使三相导线在整个线路长度上的空间位置趋于对称，是当前解决长距离特高压输电线路电力系统不平衡度的常用方法。在超高压输电线路中，可以通过调整导线的换位方式和换位点，来保证线路长度较长时输电线路电力质量的稳定[2]。

武汉—南昌—长沙1000 kV特高压交流输电线路工程全线路径总长度为750.5 km，武汉—南昌段长405.3 km，南昌—长沙段长345.2 km。采用电磁暂态仿真软件ATP-EMTP，对该线路不平衡度进行仿真计算，对不平衡度的影响因素进行讨论分析，并对换位方式进行研究，推荐合理的换位方式。

1 计算模型

所建电力线路模型采用三相电压源供电，另一端采用三相等效负载，保持模型输送的功率、电压以及功率因数与额定值相当。

1.1 架空线路模型

架空线路用π型等值电路来模拟，其结构如图1所示。采用EMTP的LINE CONSTANT子程序，根据架空线路空间方位及参数，采用Carson模型进行仿真计算。

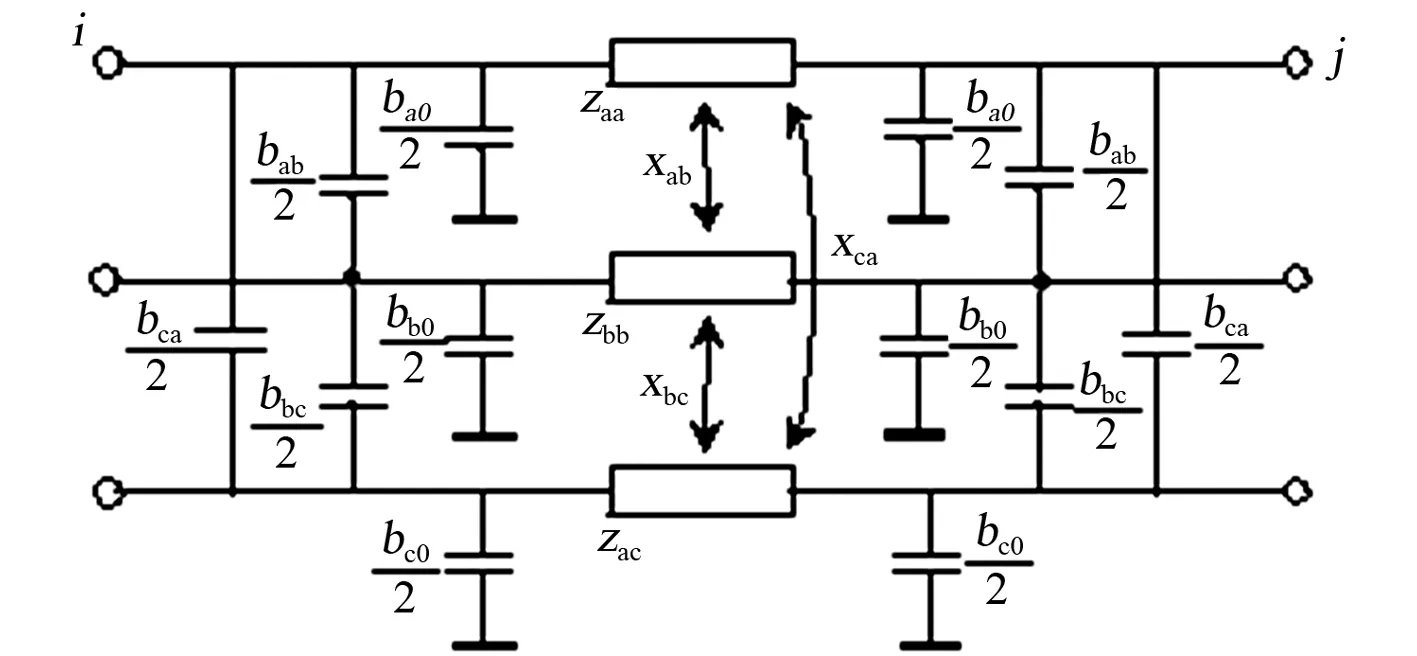
图1 三相输电线路π型等值电路

按照1000 kV输电线路杆塔结构，在ATP中建立三相架空线路模型，其结构如图2所示。

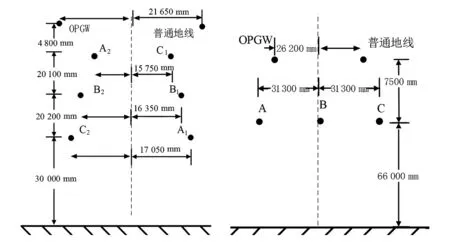
图2 线路模型

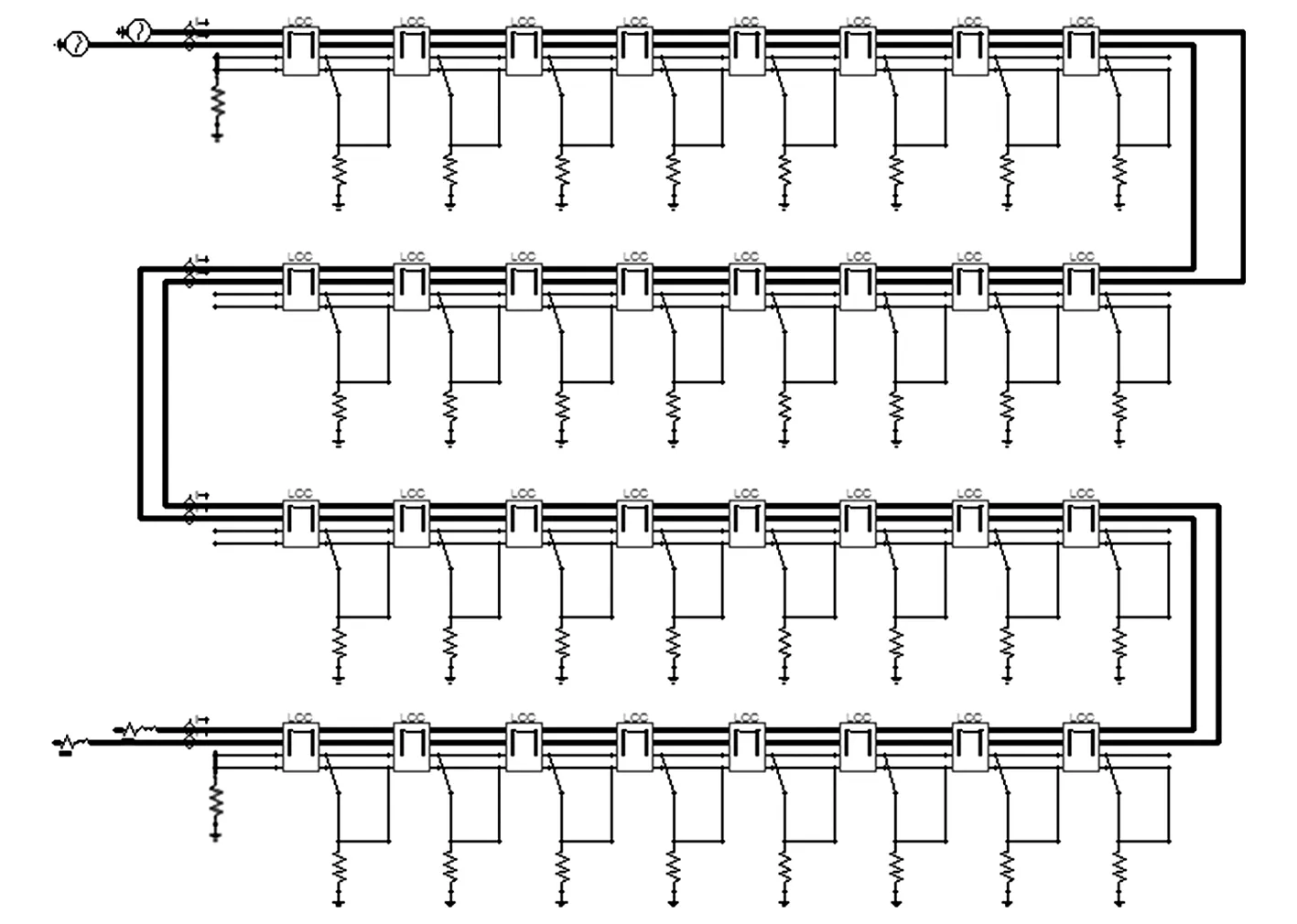
图3 线路分析模型

1.2 线路分析模型及计算方法

基于架空线路模型，在ATP-EMPT中建立三相架空线路不平衡度分析模型。

线路模型三相电源电压为1000 kV，架空线路模型分为多个小节，每节采用p型等值电路进行仿真计算。得到线路模型负载端的电压电流波形，利用相-序变换矩阵求解正、负序分量[3]，对于电压有：

式中，a=e120。根据标准规定公式计算εU及电流不平衡度εI，由于分析中采用对称负载，因此只需计算εU[4]。

1.3 其他计算参数

武汉—南昌—长沙1000 kV特高压交流输电线路工程最高运行电压是1100 kV；输送功率是5000 MW；功率因数为0.95。工程所用到的导地线参数如表1所示。

表1 导地线参数

2 线路不平衡度分析

2.1 线路长度对不平衡度的影响分析

使用线路分析模型在ATP-EMPT软件进行仿真计算，线路三相电压与电流波形如图4、图5所示，不平衡度计算结果如表2所示。

由表2可知，线路不平衡度随着线路长度的增加而增大。武汉—南昌段与南昌—长沙段的不平衡度差距较大的原因是两段线路的单回路比例不一样，武汉—南昌段单回长度占2.1%，南昌—长沙段单回长度占19.7%。同时也可以看出武汉—南昌段在长度为220 km时不平衡度就超过了2%的限值要求；南昌—长沙段在长度为140 km时不平衡度就超过了2%的限值要求。

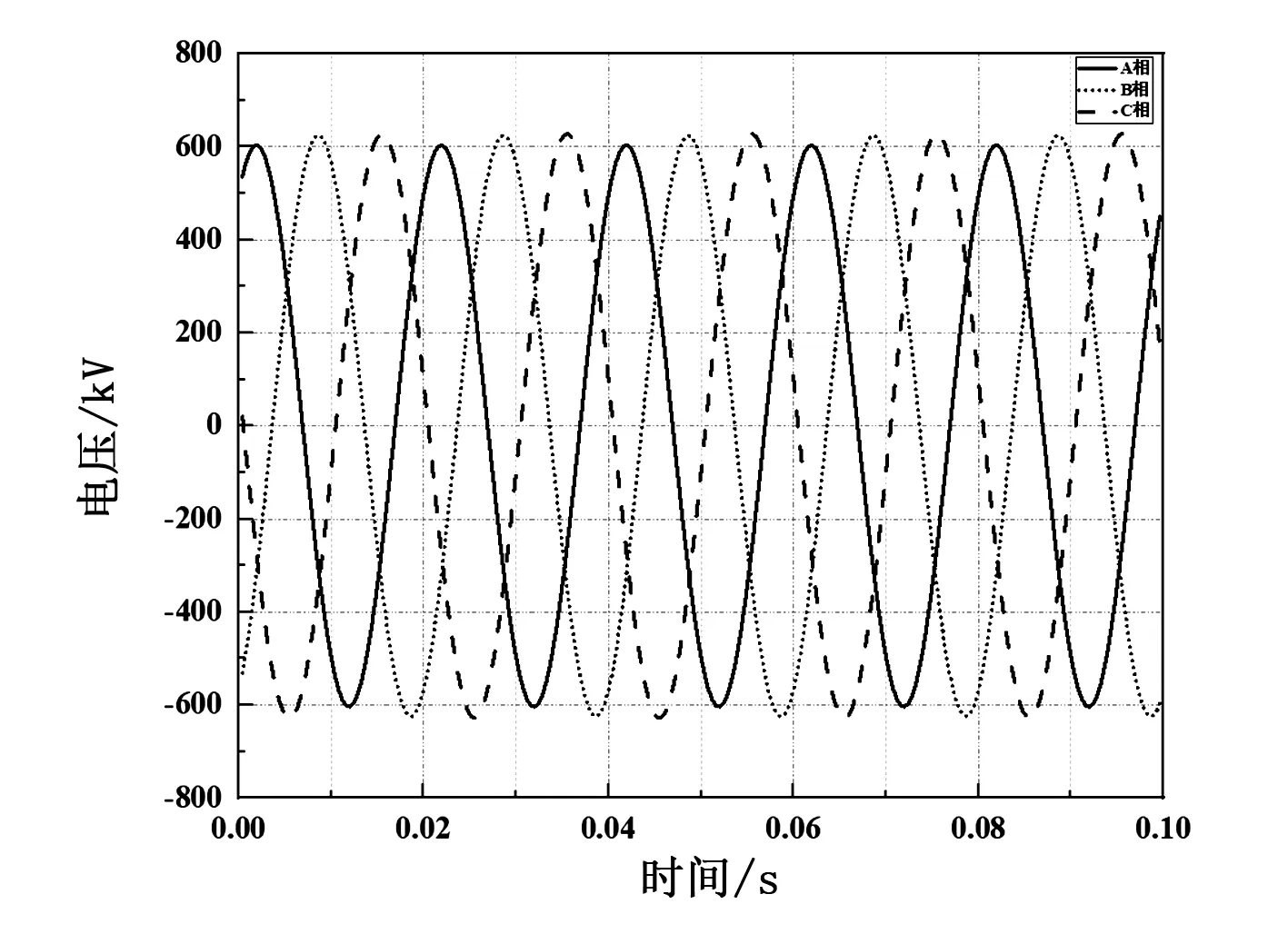
图4 电压波形

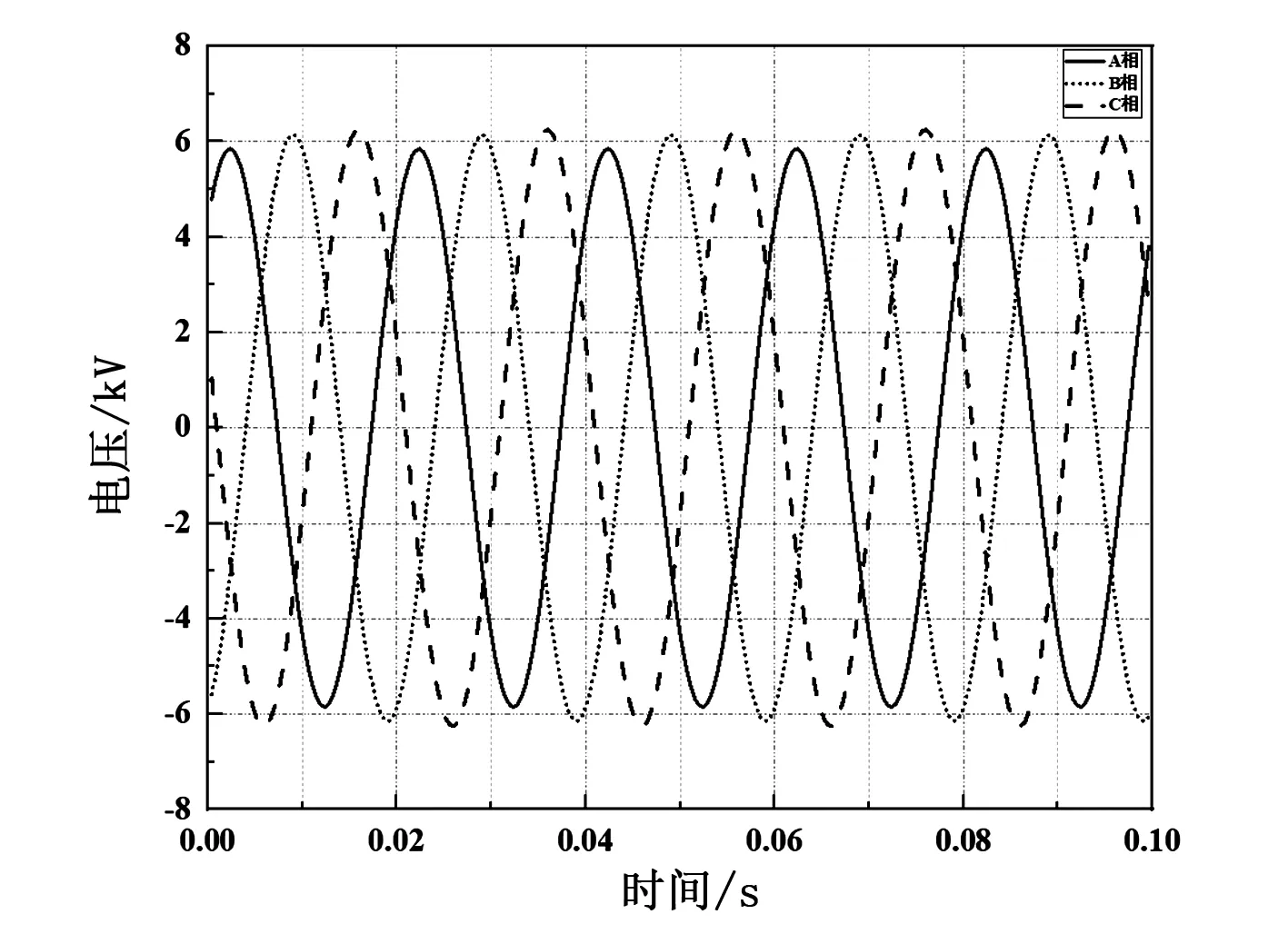
图5 电流波形

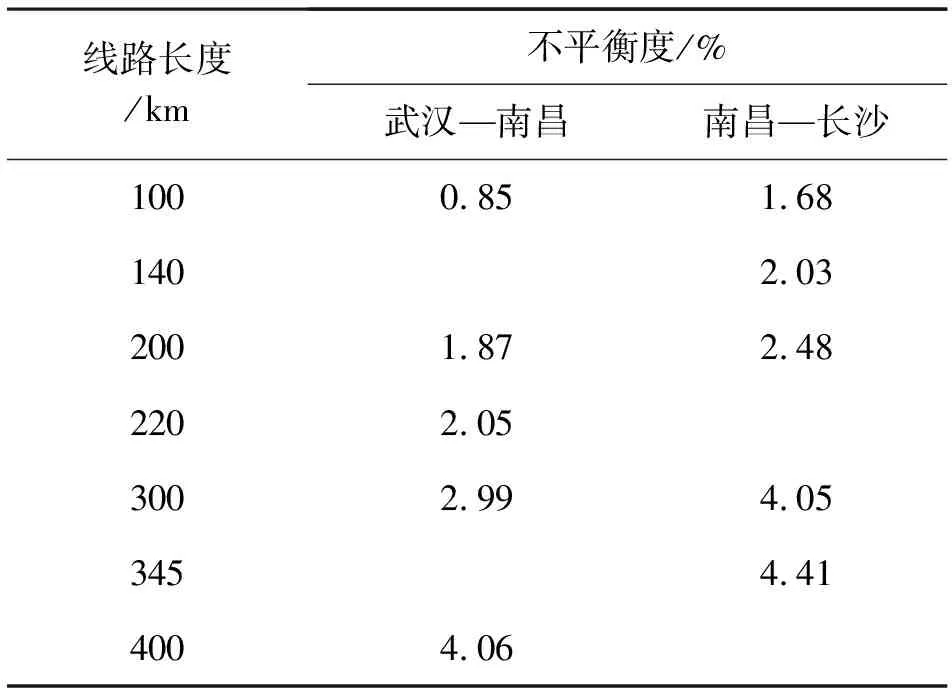
表2 线路不平衡度

2.2 导线对地高度

采用工程给定的系统参数以及杆塔数据，对武南段400 km不同杆塔呼高下的不平衡度进行仿真计算，结果如表3所示。

表3 导线对地高度对不平衡度的影响

从表3可知，输电线路不平衡度受到导线对地高度的影响微小，在实际工程中可以不计。

2.3 相序对不平衡度的影响

武汉—南昌—长沙工程中同塔双回全部采用逆相序，为研究相序对不平衡度的影响，用相同的系统参数计算同塔双回线路不同相序情况下，线路的不平衡度，计算结果如表4所示。

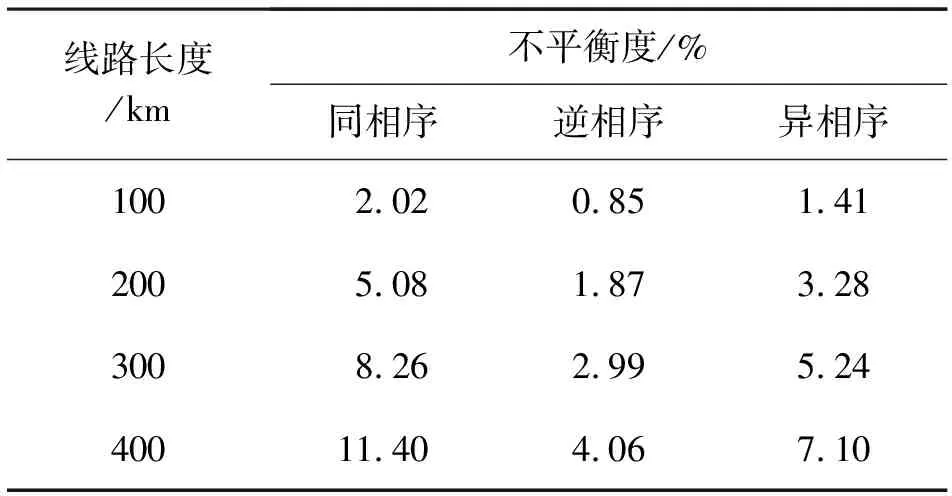
表4 不同相序下线路不平衡度

上述结果表明，导线同相序排列时，双回输电线路的不平衡度最高，导线异相序排列时线路的不平衡度较低，逆相序排列时不平衡度最低。

对同相序排列线路，超过100 km需要换位；对于采用异相序排列方式的线路，超过160 km需要换位；对于逆相序排列方式的线路，超过220 km需要换位。

同塔双回线路间存在电场和磁场耦合，两回路间相互干扰，同相序运行方式下，两回路间的干扰是相互加强的，由此引起不平衡度增加；而在逆相序和异相序排列方式下，两回间的干扰是相互削弱的，双回线路的不平衡度减小。

2.4 土壤电阻率对不平衡度的影响

武汉—南昌—长沙1000 kV特高压交流输电线路工程跨越3省9市，地理位置跨度大，地质不同，需研究土壤电阻率对不平衡度的影响。

针对400 km长的同塔双回及单回线路，建立仿真模型，计算了不同土壤电阻率的情况下线路的不平衡度，计算结果见表5。

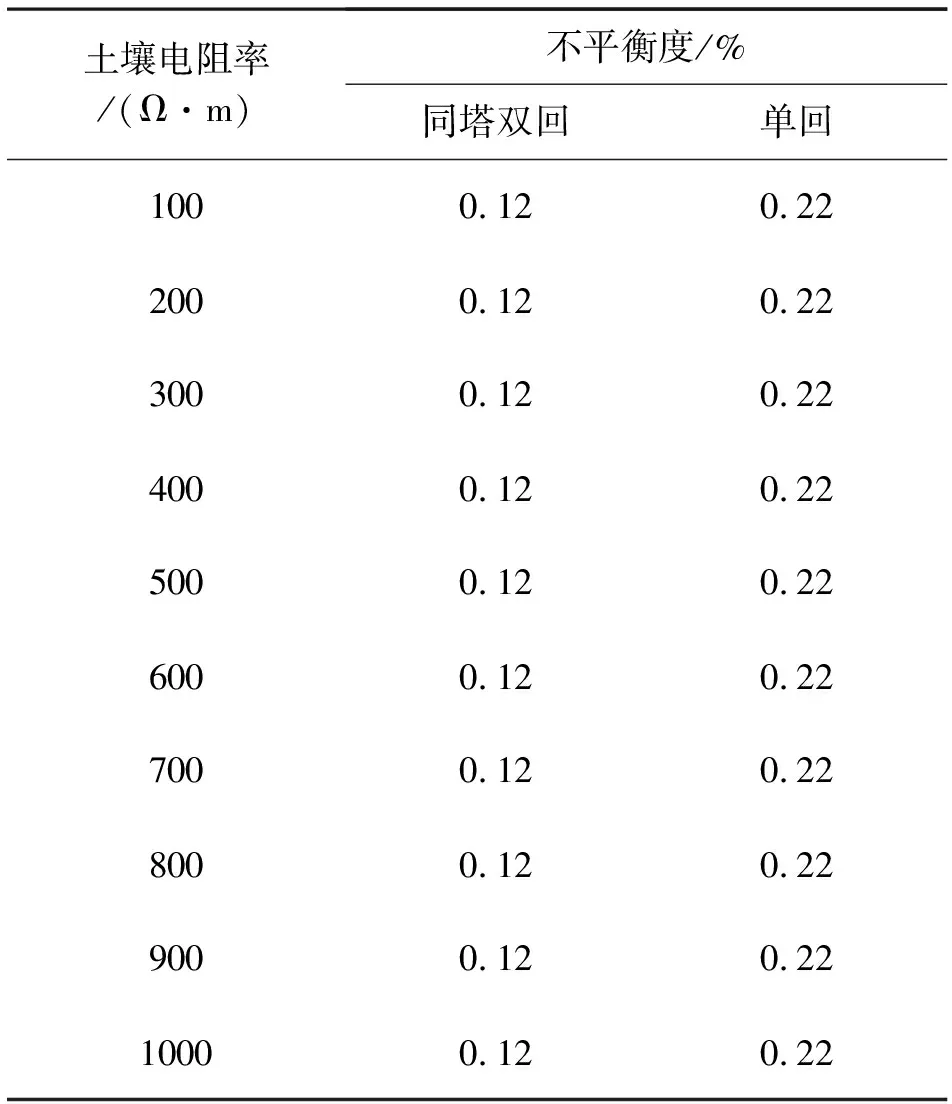
表5 不同土壤电阻率下线路不平衡度

由表5可知，土壤电阻率对输电线路不平衡度的影响很小，可以忽略不计。

3 全换位后线路不平衡度分析

3.1 全换位后线路不平衡度

图6为线路换位示意图，换位后达到首端和末端相序一致，每种相序排列各占1/3的线路长度，构成一个整循环，称为一个全换位[5-6]。

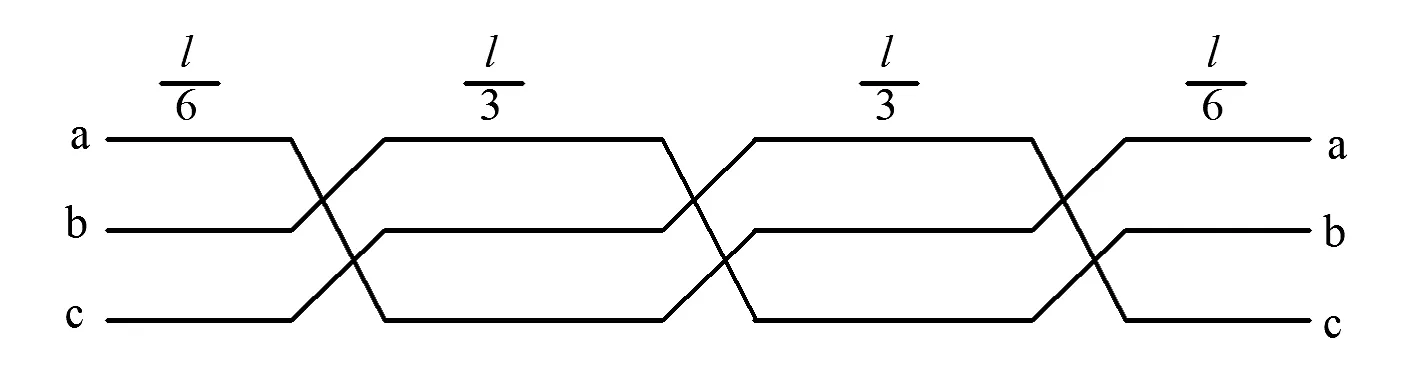
图6 线路一个全换位

利用EMTP的换位元件，在EMTP电磁暂态计算程序中，一个输电线路全换位的模型示于图7。

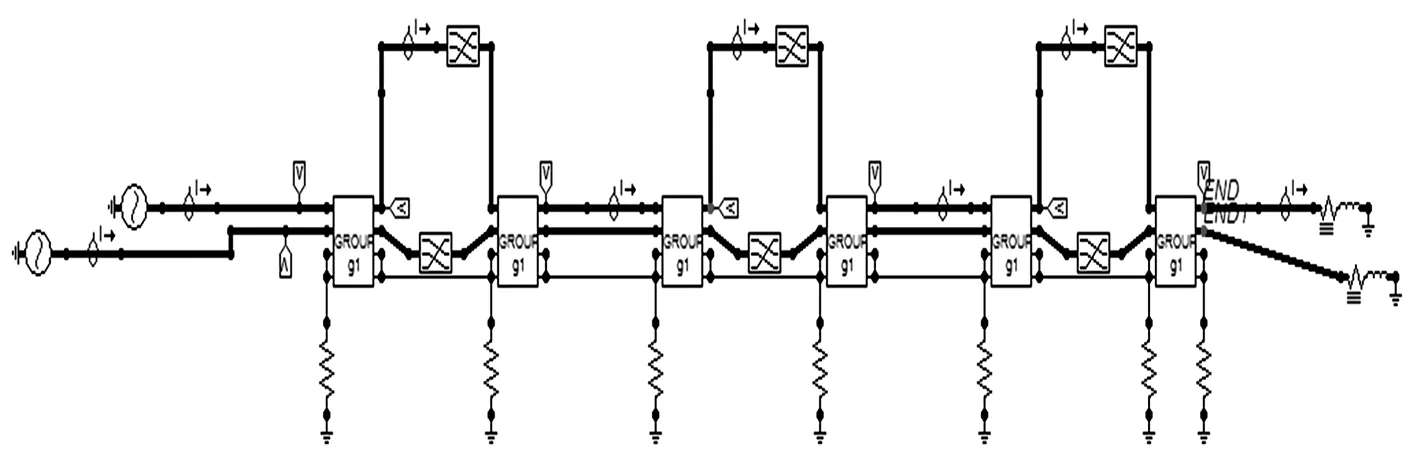
图7 EMTP中一个全换位计算

使用此模型计算线路不平衡度，图8、图9为一个全换位后线路负载的电压、电流波形，表6为不平衡度的计算结果。

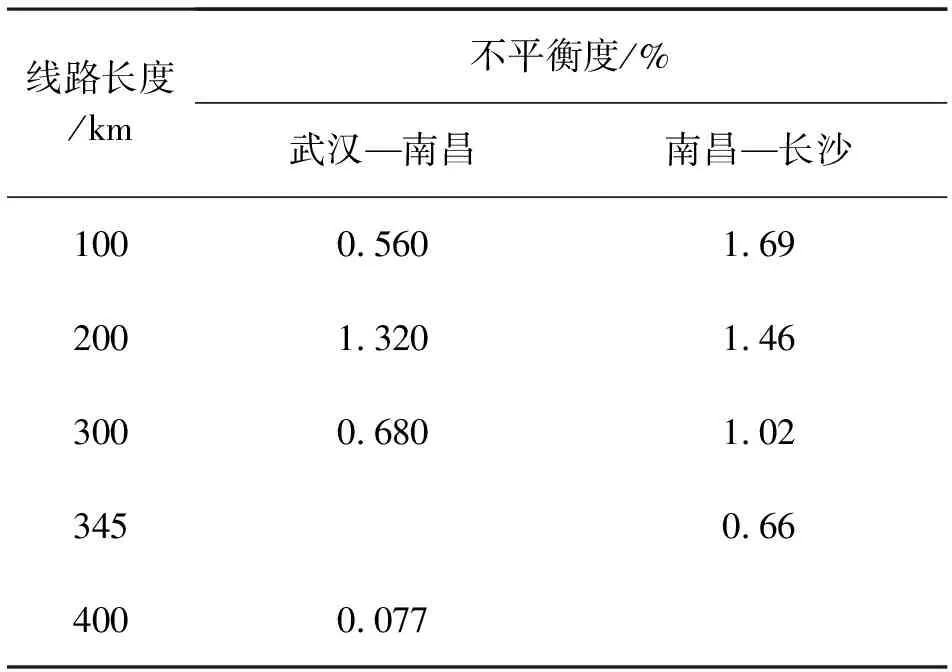
表6 一次全换位后线路各段不平衡度

图8 一次全换位后线路电压波形

图9 一次全换位后线路电流波形

从表6中可以看出，经过一次全换位后，线路电压不平衡度显著减小。按照国家标准GB/T 15543-2008《电能质量三相电压允许不平衡度》的要求[7]，对垂直排列线路，一次全换位能满足电压不平衡度要求的长度远大于400 km。

按照武汉—南昌和南昌—长沙两段分别进行一次和两次全换位后线路不平衡度如表7所示。

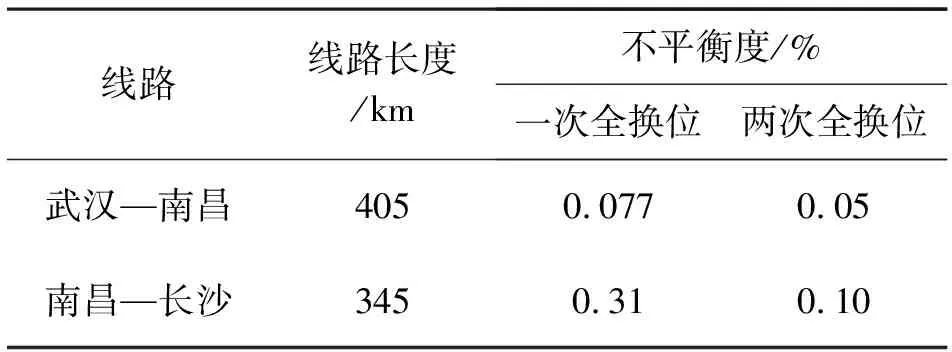
表7 全换位后不平衡度

从表7可看出武汉—南昌—长沙1000 kV线路进行一次全循环换位后，线路不平衡度小于2%的限值，满足要求。

3.2 不同长度线路全换位后不平衡度

为研究一次全换位后线路长度对不平衡度的影响，保持计算用系统参数和塔头尺寸不变，分别针对同塔双回及单回线路，按照图7所示换位方式，建立仿真模型，计算了不同线路长度的情况下线路的不平衡度，计算结果见表8。

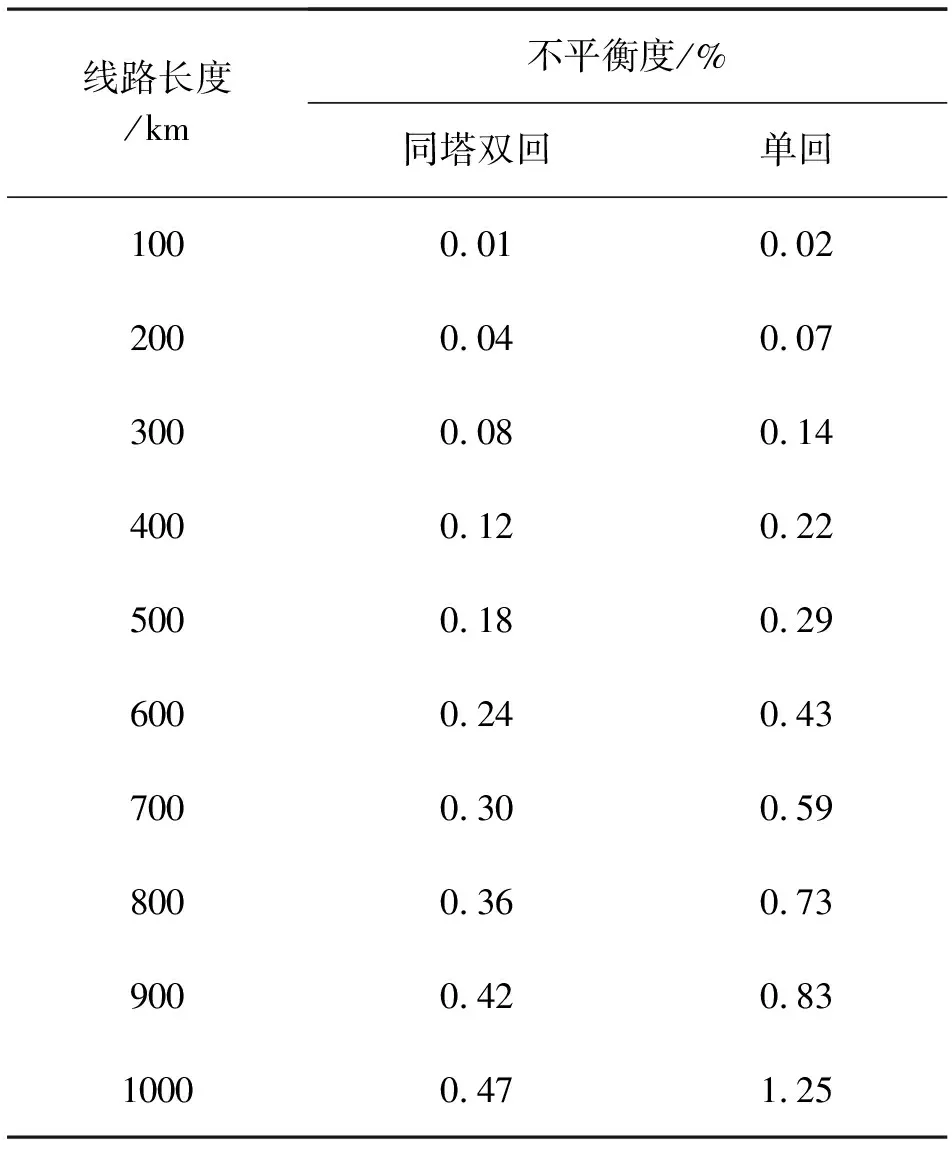
表8 换位后线路长度对不平衡度的影响

由表8可知，按照实际工程的塔头及系统参数，一次全换位后线路不平衡度能满足限值要求的长度大于1000 km。使用多项式拟合可知，同塔双回路不平衡度达到2%限值时的长度约为2700 km，单回线路达到2%限值时的长度约为1600 km。

4 结 语

综合前面的计算、分析和研究，主要结论如下：

1)导线对地距离对线路不平衡度几乎没有影响。随着水平线间距离的减小，不平衡度有所减小，随着垂直线间距离增大，不平衡度有所减小。

2)运行电压、输送功率和线路不平衡度的关系：在运行电压一定的情况下，不平衡度随输送功率的增大而增大；在输送功率一定的情况下，不平衡度随运行电压的升高而减小。

3)同塔双回路的不平衡度高于单回路。

4)导线同相序排列时，双回输电线路的不平衡度最高，导线异相序排列时线路的不平衡度较低逆相序排列时不平衡度最低。对同相序排列线路，超过100 km需要换位；对于采用异相序排列方式的线路，超过160 km需要换位；对于逆相序排列方式的线路，超过220 km需要换位。

5)按照所研究的实际工程的塔头及系统参数，一次全换位后线路不平衡度能满足限值要求的长度大于1000 km。使用多项式拟合可知，同塔双回路不平衡度达到2%限值时的长度约为2700 km，单回线路达到2%限值时的长度约为1600 km。