Deviations form Taylor Rule and Asset Booms: Empirical Analysis based on DCC-GARCH and Wavelet Analysis

Ru Qiu

Abstract：In this paper， DCC-MGARCH model and Wavelet Analysis are used to explore the relationship between the deviation from Taylor Rule and the Asset Boom. The DCC-MGARCH model shows a significant negative correlation between the two indicators in dynamic process， while the Wavelet Analysis further confirms the negative correlation particularly in the long-term band. The results from the empirical analysis suggests that the deviation from Taylor Rule is not likely to be the major cause of the Asset Boom. Moreover， monetary policies are more likely to behave in a negative feedback mechanism for the sharp growth in asset prices.

Keywords：Taylor Rule， Asset Boom， DCC-MGARCH， Wavelet Analysis

1.Introduction

As happened in the 1929 Great Depression and 1980s Japanese asset bubble， the sharp asset price reversals were often followed by protracted recessions and deflation. Therefore， the linkage between monetary policy and asset price movements has been intriguing for many of the economists and essential for the policy makers for a long while （Woodford and Michael， 2001）. [1]

Many of the central banks in industrial countries nowadays follows some version of the Taylor Rule. In the U.S.， it is suggested that the Federal Funds Rate should follow a response mechanism to changes in inflation and the output gaps （Allen and Kenneth， 2011; Aielli， 2013）. The debate over whether the deviation from the Taylor Rule caused the housing boom in U.S. and should the monetary policy target asset booms have been thrown into sharp relief. [3，8]

In this paper， the DCC-MGARCH model is used to test the dynamic correlation between the deviation from Taylor rule and the growth in asset prices， then apply the Wavelet Analysis to further investigate the relationship between the two indicators， and finally discuss some variants and the evolvement of the Taylor Rule.

The remainder of this paper is organized as follows. Section 2 does a brief introduction to the original form of Taylor Rule， Section 3 introduces the data and methodology used in this paper， Section 4 presents the empirical findings of the research， Section 5 discusses some variants of Taylor Rule， Section 6 presents my conclusions.

2.Theoretical Literature

Taylor （1993） has proposed a straightforward formula to describe U.S. monetary policy by an interest-rate feedback rule [4]：

whereis the federal funds rate，is the rate of inflation over the previous four quarters， y is the percent deviation of the real GDP from a target， Y is real GDP andis trend real GDP. Taylor， later in his Taylor （1999）， argues for the normative significance of this rule based on the fact that it describes U.S. policy in such a period where monetary policy is widely considered to have been extraordinary successful， suggesting that this rule is worthy of adopting as a principle of the design of monetary policies. [6]

Based on the existing literature， MGARCH is a dynamic multivariate regression model where the conditional variances and covariances of the errors follow an ARMA structure. In order to eliminate negative risk of a nonlinear combination of univariate GARCH models with time-varying cross-equation weights， the DCC GARCH model proposed by Engle （2002） is used to model the conditional variances matrix of errors， which can be written as follows [7]：

is an m*1 vector of standardized residuals，，andare parameters that govern the dynamics of conditional quasicorrelations. andare nonnegative and satisfy. If theis stationary， the R matrix in equation 2 is a weighted average of the unconditional covariance matrix of the standardized residuals，denoted by， and the unconditional mean of， denoted by. Because ， as shown by Gian Piero. （2013）， R is neither the unconditional correlation matrix nor the unconditional mean of. For this reason， the parameters in R are known as quasicorrelations.

According to Engle （2002）， the estimation of this model is done through using a two-step maximum likelihood estimation method; and the likelihood function is given by [7]：

While the DCC MGARCH model could offer information on the dynamic relationship between the deviation from Taylor Rule and asset prices， it is focused on a fixed scale （i.e.， quarterly）. However， the real estate market often consists consumers and investors operating at different time scales. It is possible that the relationship between the federal funds rate deviated from Taylor Rule and the asset prices could die down in the short-scales （high frequency）， or it could transfer to the higher scales （low frequency）. The Continuous Wavelet Analysis could then be employed to capture the dynamic relationship between the two indicators in different time scales.

The continuous wavelet transform expands the time seriesandinto a time-frequency plane. Based on a mother wavelet， a family of“wavelet daughters” is defined as：

whereandis defined as equations 12 and 13， respectively， and * denotes the complex conjugation. According to the equations 13 and 14， the partial wavelet coherency can be obtained as . The interpretation of the partial phase-differenceis consistent with.

In this study， quarterly growth rate of each variable is used to present the wavelet property. Hence， stands for the growth rate the deviation from Taylor Rule， denotes Real Property Prices growth rate in U.S.， andrepresents interest rate， which is the control variable. The continuous wavelet analysis in this paper is processed by the MATLAB ASToolbox.

3.Data and Methodology

The Real GDP， Real Potential GDP， and Consumer Price Index （as the indicator of Inflation Rate） are collected form the FRED， and the suggested Federal Funds Rate are derived by using equation1. Combined with the data of Effective Federal Funds Rate， the deviation data in the form of a time series form 1980Q1 to 2018Q4 is generated. For simplicity， Deviation is used to denote the gap between Effective Federal Funds Rate and the suggested rate given by equation1. Meanwhile， the data of Real Residential Property Prices is also collected as an indicator of Asset Prices in this study. All the quarter data are collected from FRED.

According to the DCC MGARCH model and Wavelet Analysis mentioned above， the analysis of the relationship between the deviation and the asset price growth during the period of 1980-2018 in U.S. is presented.

Figure 1： Effective Federal Funds Rate v.s.  Figure2： Asset Price Growth v.s. The

suggested by Taylor Rule                              Deviations

From Figure 1， although synchronous movements are seen between Effective Federal Funds Rate and the rate suggested by Taylor Rule， the deviation between the two rates are getting larger. Meanwhile， it is not so obvious to tell the relationship between the deviation and Housing Boom from Figure 2.

The summary statistics and diagnostic test results of the deviation and asset prices are presented in Table 1. it is evident that both the deviation and asset prices exhibit skewness and fat tails. The JB statistic values show evidence towards non-normal distribution. Meanwhile， the diagnostic test results confirmed the ARCH effect in both of the series. Based on the results shown， MGARCH modelling is proceeded next.

From the DCC GARCH results， it is evident that there exists significant negative correlation between the deviation and the growth of asset prices， indicating the monetary policy may behave as a negative feedback mechanism to the housing boom. The parametermeasures the impact of the standardized residual product to dynamic correlation coefficients while shows the persistent feature of correlation. From the parameter estimation， it is not hard to see that the linkage between the deviation and asset prices is highly persistent in nature. Moreover， the fluctuations in asset prices could be largely explained by its own past values rather than the deviation.

Figure 3 presents the wavelet power spectrum of the deviation from the Taylor Rule. The time dimension is showed on the horizontal axis， and the vertical axis represents the period cycles （years）. It clearly shows that the deviation from Taylor rule went through significant

volatilities in the period of mid-1980s and 2005-2007， which is in a period that the nation

was going through a great boom in housing market， the significance area relative to

frequency axis indicates the deviation might need up to 4 years to smooth.

Figure 3 The Wavelet Power Spectrum

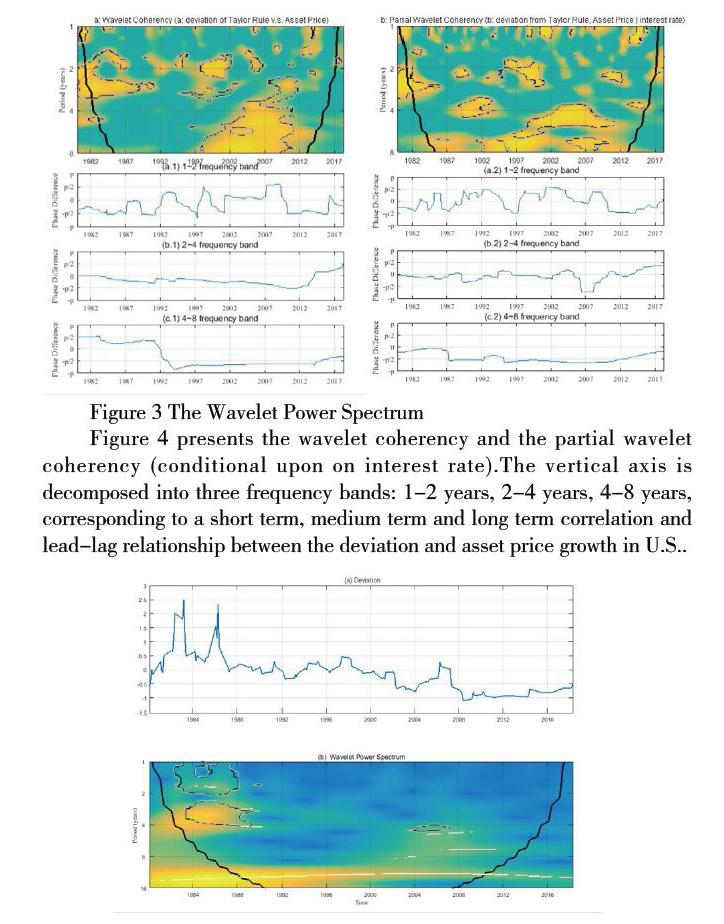
Figure 4 presents the wavelet coherency and the partial wavelet coherency （conditional upon on interest rate）.The vertical axis is decomposed into three frequency bands： 1-2 years， 2-4 years， 4-8 years， corresponding to a short term， medium term and long term correlation and lead-lag relationship between the deviation and asset price growth in U.S..

Figure 4 The Wavelet Coherency and the Partial Wavelet Coherency

The wavelet coherency indicates the correlation between the deviation from Taylor Rule and growth in asset prices， in which significant regions could be found particularly assembled in between 2000 and 2007， when the housing market is going through a boom. An interesting conclusion arises when looks at the phase-differences： In the short term， the correlation going through， periodically changes its sign; while in the mid-term to long-term， there is a relatively stable negative correlation. This is useful to tell the fact that the monetary policy deviating from Taylor Rule， in the short term， the impact is indistinguishable; however， in the relatively long run， gives a negative feedback to the asset boom.

4.Extended Discussion

While the Taylor Rule has successfully incorporated several features of optimal monetary policies， the original formula of the rule gets improved upon. The measurement of the output gap proposed by Taylor （1993） might have been quite different from the theoretically correct measurement， for the fact that the natural rate of output could be impacted by a wide range of real disturbances.[4]

Bordo and Olivier （2002） proposed a non-conventional， nonlinear Taylor Rule， highlighting both the potential benefits and the limits of a proactive monetary policy. In their model， the optimal monetary policy， in a nonlinear way， depends on several macroeconomic factors but also the expectations from private sectors. Boehm and Christopher （2019） further analyzed the optimal Taylor Rule for which output and inflation are imperfectly observed within the standard New Keynesian model. They found that it is optimal to infinitely respond to estimated deviations from the targets， and suggested that the central banks may be systematically underreacting to the estimated output gap and inflation. [2，5]