基于分治策略实现模式化构建递归函数
杨勇

摘要:递归算法在程序设计的许多领域都有重要应用,为了写出思路清晰,逻辑严谨的递归函数,以分治策略为基础,归纳出组成递归函数的三大部分:提前终止条件,子问题分解,结果合并。并探讨了子问题分解的几种模式,研究了各种模式下递归函数的设计思路,为模式化构建递归函数找到可行途径。
关键词:递归;分治策略;子问题分解;回溯;栈区
中图分类号:TP311.11 文献标识码:A
文章编号:1009-3044(2020)01-0264-03
1背景
c语言程序由函数组成,通过函数之间的调用完成程序功能。如果函数在其执行语句中又调用自己,形成函数的递归调用。递归在数据结构和算法设计领域应用非常广泛,但函数递归调用一直是c语言学习和研究中的一个难点。对递归中函数调用顺序,函数返回值,递归终止条件有许多模糊的,错误的认识,不能正确地推理递归结果。对运用递归方法写出思路清晰,代码简洁的递归函数则更视为畏途。本文分析了递归过程系统底层运行机理,对编写递归函数的思路做了探讨和分析。
2递归调用系统底层运行机理
递归调用是一种特殊的函数嵌套调用。当一个函数中某个语句开始调用另外一个函数时,在操作系统底层上意味着当前正在运行的一段执行指令序列中途暂停,不往下执行,转而去执行另一段指令序列。执行完毕后,又回到原来执行序列的暂停位置处,从暂停位置开始继续往下执行。每一个函数被调用时,系统都将为其分配栈区空间,把函数形参和局部变量放在栈区空间里。函数运行结束,则系统回收为该函数分配的栈区内存,栈顶指针下移。一个函数调用自己,实质上与函数去调用其他函数没有任何区别,也将为之分配独立的栈区空间,放置各自的形参和局部变量。例如F(int a)函数:
函数执行到语句F(a-1);时,以参数a-1调用自己,系统为F(a01)在栈区空间分配内存,存储F(a-1)函数的形参和局部变量。F(a-1)函数执行时会再次调用自己,形成循环,这个循环是不能结束的,系统也不断在栈区为新调用的F函数分配内存。直到栈区空间耗尽。因此必须有一个终止循环调用的机制,我们在函数调用自己的语句之前,设定某种条件,当条件满足时,函数提前结束。本函数结束了,前面处于等待状态的函数按调用的逆序逐个结束,整个递归也就可以终止。
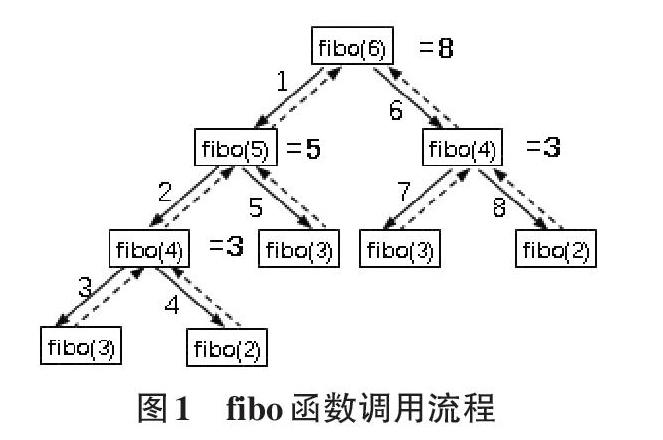
以求斐波那契数列为例,解析递归函数调用过程。参数n为斐波那契数列的项数,以0开始,设n=6,每次调用以方框表示,画出调用图示:
图1中实线箭头表示调用方向,数字表示调用顺序,虚线表示函数返回位置。调用过程形成二叉树的形式,但实际运行时,这些分支不会同时运行,调用中始终只存在单链。fibo(6冲进入递归时的语句为fibo(5)+fibo(4),实际上,第二个函数调用fibo(4)并没有开始,要等到fibo(5)调用返回后,才会进2k.fibo(4)。依次类推,进入fibo(5)后先调用fibo(4),进2k.fibo(4)后先调用fibo(3),由于fibo(3)满足提前返回的条件,开始返回,不再递归,返回2,回到fibo(4)中,fibo(4)再开始调用fibo(2),不递归,得到结果1,与fibo(3)的返回结果相加得3,fibo(4)调用结束返回3回到矗一bo(51中,后面调用过程可作类似分析,不再赘述。
分析递归过程的例子,总结出如下一些特征:
1)函数递归调用时,形参在不断变化,一般来说,形参的值向缩小的放向变化,直到触发提前结束函数的条件,当前运行函数不再递归,函数按调用的逆序依次结束。
2)每个被调用的递归函数都拥有独立的栈区空间,各函数的形式参数和局部变量处于不同的栈区空间里,相互独立。
3)整个递归调用可以有多个分支,但分支不会同时运行,调用链始终为单链,只有链条末端的函数在运行中,而其他函数则处于暂停状态。
3运用分治策略构建递归函数
递归函数解决问题的过程,实际上是算法中分治策略的体现。所谓分治,是把一个复杂问题分解为若干子问题,若子问题有简单的方法得出解,整个问题的解则是所有子问题解答的合并。如果分解出的子问题仍然不易解决,则继续对子问题分解,直到分解为能解决的子问题为止,函数递归的过程就是对复杂子问题分解的过程。回溯算法也经常使用递归来实现。回溯算法中的子问题之间,是相互关联的,下一個子问题的解依赖于上一个子问题的解。分治算法中的子问题也有一定的关联性。只是没有回溯算法中那么紧密。从大的角度来看,回溯算法也属于分治策略。
以分治策略为基础,为使求解过程遵循较为固定的步骤,将递归函数大体分为三部分:
第一部分:写出提前终止,不再递归的条件。当递归函数不断调用,问题不断分解,规模不断缩小,缩小到一定边界之内,符合一定条件时,此时的子问题是一个最简子问题,可以直接解决,无须进一步递归。条件设定一般由函数形参的变化来完成。
第二部分:问题分解。分解成两个或多个子问题,简单子问题直接解决,复杂子问题不能直接解决,交给递归函数。解决子问题的算法应该与解决整个问题的算法完全相同,区别只在于处理的规模不同,或处理时的参数不同。要注意的是,子问题分解,有时需要先做一定的前处理工作,之后才能明晰的划分子问题。
第三部分:子问题结果合并。简单子问题的解很直观,而复杂子问题的解是什么?就是递归函数的返回值(如果没有返回值,则是函数运行中的所有输出值),这是理解结果合并方法的要点。合并可以是子问题的解经过简单计算后合并。也可以是复杂处理运算后再合并。
递归函数三个组成部分中,第二部分如何正确划分子问题,是设计递归函数的关键。把子问题分解模式归纳为如下几种,并按上述三大部分来构建递归函数。
3.1问题=1个简单子问题+1个复杂子问题
简单子问题直接在函数中解决,复杂子问题交由函数递归解决。这是递归函数最常见的问题分解模式。例,求字符串“ABCD”的全排列:
1)问题:输出字符串全排列。
2)简单子问题:字符串第一个位置作全排列(即字符串中各個字符轮流放在第1位1
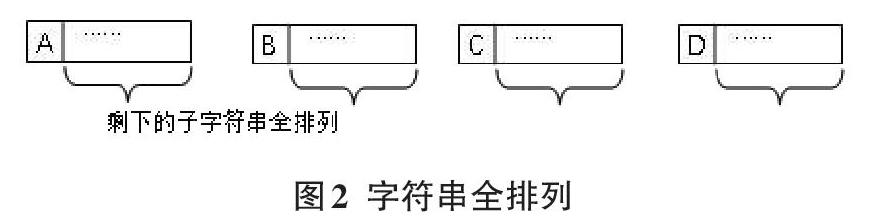
3)复杂子问题:除开第一个字符,剩下的子字符串再做全排列,以图示表示:
4)提前结束条件:剩下的子字符串只有一个字符了
5)结果合并:当剩下的字符串只有一个字符时,全排列完成,输出整个字符串
通过循环把各个字符轮流交换到第一个位置,剩下的少了一个字符的字符串再做全排列,其算法同整个字符串全排列完全相同,交由函数递归完成。递归调用时,传给函数的字符串会越来越短,当传入函数的字符串只有一个字符时,无须再排列,函数提前结束,不进入递归。写出字符串全排列函数如下:
简单子问题与复杂子问题的结果合并时,要注意合并的顺序,有时,复杂子问题的结果要置于简单子问题的结果之前。例如将整数转换为字符串输出,思路如下:
1)问题:整数转为字符串
2)简单子问题:把整数的个位转为字符。(求整数对10的余数可得个位数)
3)复杂子问题:整数去掉个位后的部分整数转为字符串,递归调用求解。
4)提前结束条件:整数只有个位了,直接转为字符。
5)结果合并:先输出递归函数结果,再输出个位转换结果。
整数转为字符串一定是前面的部分整数先输出,再输出最后个位字符,所以递归函数要放在个位字符输出之前。再进一步思考,如果改变合并顺序个位字符先输出,递归函数后输出,那么结果将得到原整数的倒序字符串。
3.2问题=1个复杂子问题+1个复杂子问题。
这种情况两个复杂子问题都由函数递归解决。然后将两个子问题的结果合并。合并时有简单合并,也有经过复杂处理后再合并。例如,求二叉树的高度,问题分解得:
1)问题:求根为root的二叉树的高度
2)复杂子问题一:求二叉树根的左子树高度,递归调用求解
3)复杂子问题二:求二叉树根的右子树高度,递归调用求解
4)提前结束条件:所求树为空树,根是NULL,高度为-1;
5)子问题合并:左右两个子树高度的较大值+1为整个树的高度
很多情况下,子问题划分工作并非简单明了,必须先做一定的处理,才能开始划分。例如快速排序法,对于要排序的数列,选取一个中间数,将其余数置于中间数的两边,小数在左边,大数在右边,对以中间数为分界的两个子序列分别排序,合并起来就是整个数列的排序。排序函数qnisort执行过程是:
1)提前返回条件:子序列只有一个元素
2)子问题划分前处理:选取中间数,将其余元素按左小右大的原则分别置于中间数的两边。
3)划分子问题:复杂子问题一:对中间数左边序列排序递归调用quicksort
4)划分子问题:复杂子问题二:对中间数右边序列排序递归调用quicksort
5)左右两个排序子序列合并。
3.3复杂问题=n个复杂子问题之和
如果各复杂子问题算法相同,但是各子问题传人参数与子问题解决的先后顺序有关。这时可以采取依照一定顺序逐个解决子问题的策略。例如著名的八皇后问题:8x8的国际象棋盘上放上8个皇后,任意两个皇后不能在同一行,列或对角线上。问有多少种摆放方法?分析:8个皇后只能处于不同列上,即一列上只能摆一个皇后,各列上皇后摆放的行不能相同,对角线也不能冲突,由此将问题抽象为:在棋盘不同列上为每一个皇后找到符合条件的行位置,当八个列上都摆上皇后时,就得到问题的一个解。
1)问题:依列顺序求各列皇后摆放的行
2)问题分解:有8个子问题,每个子问题是:给某列上的皇后查找正确的行位置。
3)提前结束条件,8列皇后都找到位置。或者摆到某一列皇后时,已经找不到合适的行。
4)子问题合并,当8列皇后都能找到位置时,输出结果。
建立一个数组queens[8],各元素的下标代表皇后所处的列,各元素的值代表皇后所在的行,递归函数只针对子问题求解既可,构建函数如下:
其中valid_row函数判断index列的皇后能否放在某一行上。在eight_queen函数中,对于index列的皇后,如果轮询8个行位置都找不到符合条件的行位置时,函数也将结束不产生递归,此时函数将返回到index-1列的函数循环中,继续查找in-dex-1列皇后下一个合适的行位置,递归则在另一个分支上继续进行,所以,eight_queen函数有两种终止递归的条件。
4结束语
本文探讨了函数递归调用操作系统运行机理,梳理出递归调用过程的几个关键性特征,归纳出递归函数的三大组成部分,并探讨了分治策略下问题分解的几种模式,对每一种模式下构建递归函数的思路以具体例子加以分析。以本文总结的递归构建模式,可以快速、准确地写出思路清晰,逻辑严密的递归函数。

