三维空间属性体克里金插值方法的研究
房鹏 陈丽钧

摘要:该文以克里金插值法为基础,实现了一种滑动邻域克里金方法,并针对该方法无法应用于三维空间属性体建模的缺陷,提出了一种改进算法。从属性体建模的角度,该文详细介绍了滑动邻域克里金方法基本原理,分析这种方法的优势和缺点,并提出一种改进的滑动邻域克里金方法,实现了其在三维空间中的属性插值。最后通过体绘制以切片形式展示插值结果,说明本文提出的改进算法可以应用到三维空间属性体建模,并具有较高的效率。
关键词:克里金插值;滑动邻域克里金;三维空间属性体;体绘制
中图分类号:TP3 文献标识码:A
文章编号:1009-3044(2020)01-0231-02
克里格法是国际上公认的空间插值方法,也是地质统计学的主要方法。它具有线性,无偏和最小方差估计的特点。克里金算法原型为普通克里金,由于该算法实现比较简单,本文在实现普通克里金的基础上又实现了一种高效的滑动邻域克里金方法,该方法由梅钢等人提出,其原理为:以变程为边长将研究区域划分为正方形网格,构造该区域内的克里金方程组并求解得到插值结果。本文在实现该算法后又研究了大规模四维属性数据体插值,因采用普通克里金和滑动邻域克里金方法均无法对其进行插值,故对梅钢等人提出的滑动邻域克里金算法进行了改进,实现了一种局部求变程并通过漫水法进行邻域内点集填充的滑动邻域克里金方法。
传统的克里格法选择所有的已知点进行插值,计算时间较长,尤其在大规模采集数据的情况下,甚至无能为力;并且在实际中,真实的协方差是估计出来的,而数据测量时又不可避免产生误差,这就有可能导致在大的邻域上插值产生的均方差比在相对较小的邻域上插值时的均方差要大。故在计算前对每个待插点分别选择其邻域内的一部分已知点作为原始估值计算数据。因此,如何选取邻域点成了克里格法亟需解决的问题。孙立双等提出了基于空间分布权系数邻域选点算法,该算法通过建立插值点邻域点空间分布权系数的函数,确定参估值计算的邻域点。刘永社根据大量插值试验结果经验认为搜索数据采集点时搜索半径通常取1.3-2倍的变程值。牛文杰提出:利用Delaunay三角网格剖分,建立各个三角形和不同数据点的包含关系,利用三角网格的拓扑关系,检索以三角形某一顶点为共同顶点的所有三角形围成的凸多边形内包含的数据点,直到检索到的数据点满足要求。杜宇健结合温度场计算的实际应用详细分析了克里格法邻近点选择中需要考虑的原则,并采用Delaunay三角划分搜索和固定距离搜索相结合的邻近点搜索策略,提出一种利用变程的Delauuay-固定距离滑动邻域算法。梅钢等提出了一种基于变程的滑动邻域克里金方法,该方法是一种全局求变程,并根据已知变程进行局部克里金方程组计算的插值方法,弥补了Delaunay三角划分方法等需要对每个待插点必须求一次变差函数系数矩阵的逆矩阵的缺点。但是该方法有一个缺陷,即用该方法进行大规模数据插值时,进行全局变程计算量巨大因而存在无法进行插值计算的可能。为解决这一问题,本文对该方法进行了改进,实现了一种局部求变程,并通过漫水法进行邻域内点集填充的克里金插值方法。下面分别对滑动邻域克里金方法和改进的克里金属性体插值方法进行介绍。
1滑动邻域克里金插值
变差函数能反映或刻画区域化变量的许多重要性质,例如可以通过“变程”反映变量相关性的范围。滑动邻域克里金插值借鉴滑动邻域克里格法的思想,总体思路为:对所有的已知点求变程;确定矩形网格划分区域范围;将矩形区域划分为覆盖上述区域的正方形网格,网格边长即为全局变程;计算落在每个正方形单元内的已知点和待插点;以正方形单元为中心,以其相邻的正方形单元和自身单元为该单元内所有待插点的滑动邻域。值得注意的是:若邻域内已知点太少,根据正方形单元在网格中的拓扑关系向四周延展,直到满足条件。本文以三维曲面高程插值为例对滑动邻域克里金插值方法的邻域划分方式和实现步骤进行介绍:
1.1邻域划分
1.2算法实现步骤
(1)将已知采样点数据加入原始点集合。
(2)对已知所有点进行全局范围求变程a。
(3)根据求解得到的变程a,用邻域划分方法进行正方形网格单元划分。划分后的网格起点坐标为mGridXO和mGridYO。
(4)将已知原始点分配到其各自所属的网格单元。各点所在的邻域位置用公式(xO-mGridXO)/a和(yo-mGridYo)la确定。
(5)对所有待插点进行遍历确定其所在邻域,以全局变程a构建局部范围内的克里金方程组,求解方程组得到待插点结果。
2改进的滑动邻域克里金属性体插值
本文实现了基于变程的滑动邻域克里金插值方法,并在三维空间的曲面高程数据插值中得到应用,但实验证明该方法无法应用到四维属性数据体插值,一是因为属性数据体规模大,在全局范围内求解变程值会导致计算困难甚至无法得到插值结果;二是因为当采样点分布不均匀时,通过该方法得到的插值结果误差较大。
针对以上两个问题,本文对以原滑动邻域克里金插值方法做了改进,改进方案是在原算法划分网格的基础上进行更细致的二层网格划分,并且限制了邻域内最大点数和最小点数。经实验证明该方法既缩短了运算时间,又保证了插值效果的合理性。下面同样以三维曲面高程插值为例对该改进算法的步骤进行介绍:
(1)獲取已知采样点集合,用步长step进行第一层网格单元的划分,邻域划分方法与原滑动邻域算法所述一致。之后以step/3为步长对一层大网格单元进行二次划分。
(2)将已知采样点坐标分配在二层网格中,确定每个采样点在二层网格中所属的具体单元。
(3)使用漫水法,首先搜索小网格内的采样点,然后将搜索得到的点填充到其所属的一层大网格,直到大网格内达到规定的最少点数要求。
(4)根据克里金方法,对填充得到的一层网格单元内的数据点进行求解,得到该层网格内的局部变程a和理论变差。
(5)遍历所有待插点,分别确定每一待插点所在的大网格单元,根据步骤(4)求得的该网格的变程a和变差函数在当前网格单元构建克里金方程组,求解方程组得到插值结果。算法结束。
3实验结果与分析
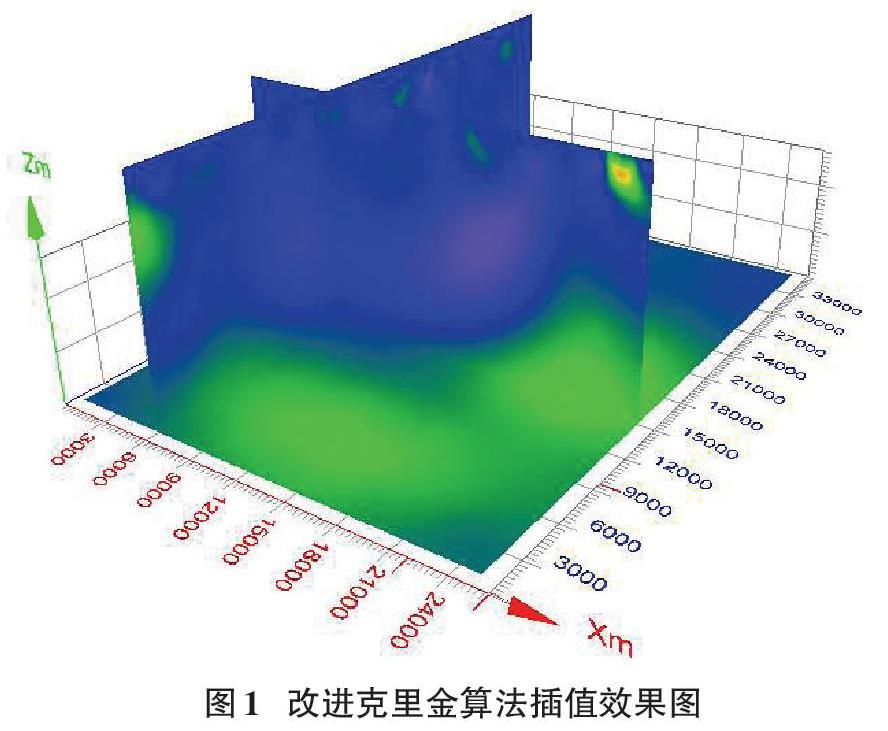
因四维属性数据体规模庞大,普通克里金和梅钢等人提出的滑动邻域克里金方法无法完成插值运算,如图1所示为改进的滑动邻域克里金插值算法对属性数据体的插值实现结果。
此次参与运算的属性样本点共有21365个,普通克里金和梅钢等人提出的滑动克里金方法经长时间计算无法完成属性数据体插值。本文改进算法耗时358s,最大误差为20.37%,最小误差为0.85%,平均误差为9.27%。因而可以看出,在数据量规模大的情况下,普通克里金和滑动克里金方法均无法完成四维属性数据体的插值运算,而本文改进的滑动克里金算法可以在上述情况下正常工作,完成四维属性数据体插值,且插值速度在可接受范围内。

