基于遗传算法优化的LSTM神经网络期货价格预测模型研究
李莹 王璐璐

摘要:该文提出一种基于遗传算法优化的长短时记忆神经网络模型(GA-LSTM)。该模型在LSTM神经网络的基础上应用遗传算法对窗宽及参数进行寻优,提高了期货价格预测的精确度,防止陷入局部最优。实验针对期货市场价格的复杂、非线性时间序列数据进行建模预测。通过结果发现模型预测效果良好,具有普遍适用性。
关键词:LSTM神经网络;遗传算法;期货价格预测
中图分类号:TP393 文献标识码:A
文章编号:1009-3044(2020)01-0182-03
1概述
随着金融市场的逐步发展,期货交易作为现货交易的一种补充方式,有着发现价格、规避风险、套期保值的作用,逐渐受到越来越多学者的关注。针对期货价格这种具有时间序列特征的数据人们通常采用传统统计模型进行研究,例如:ARIMA模型、GRACH模型等,而对于价格变动具有非线性、非平稳性的数据来说,研究效果往往不尽如人意。因此,机器学习方法逐渐被广泛应用到此类问题中。常见的机器学习算法包括:决策树、支持向量机(SVM)、神经网络。例如:黄秋萍等人在2015年进行了SVM、BP神经网络和小波神经网络模型在股票预测中的应用研究,对三种模型进行了分析比较。其中长短期记忆模型(LSTM)作为循环神经网络(RNN)的一个变种,克服了循环神经网络(RNN)面临的梯度消失的问题,具有选择性通过新信息和选择性删除旧信息的功能,不仅在自然语言处理,图像识别,文本翻译等领域广泛使用,而且在处理期货价格变化等时序数据时仍有良好表现。彭燕等人在2019年将LSTM神经网络应用在股票价格的研究当中。与其他神经网络类似,LSTM神经网络的一些参数也需要人为进行设置,很难在有限时间内找到最优参数。本文应用遗传算法(Genetic Algorithm)的全局优化能力对LSTM神经网络进行优化,寻找最优时间窗口及隐藏层神经元数目,建立神经网络模型,对期货价格变化进行预测。
2算法介绍
2.1神经网络
LSTM神经网络是基于RNN神经网络的改进,是一种深度神经网络。LSTM神经网络在RNN的基础上添加了一个用于处理信息是否有用的记忆单元,每一个记忆单元包括输入门、输出门以及遗忘门。
由于LSTM神经网络对具有时间或空间上相关特性的数据产生了良好的处理效果,因此也被广泛应用在金融时序数据的建模预测中。
2.2遗传算法
遗传算法是一种全局搜索最优解的优化方法,遗传算法工作原理与生物种群中的进化论相似,在自然界中应用交叉、变异等方式产生新的染色体。遗传算法的实现过程大致分为编码、初始化种群、计算适应度值、遗传操作这四个步骤。遗传算法因其能与其他算法结合,对其他算法进行优化和改进,从而得到快速发展,被广泛应用到各类优化问题中。
遗传算法的优点包括以下三个方面:第一,拥有良好的全局搜索能力,通过交叉、变异等手段,防止陷入局部最优解,从而取得全局最优解;第二,具有良好的兼容性,可与其他算法结合进行优化;第三,与一般寻优问题相比,对数学方面要求较低,不需建立目标函数等条件,仅需根据问题进行求解。基于以上三方面优点,本文选取遗传算法对神经网络进行优化,寻找全局最优解,进行建模。
2.3模型建立
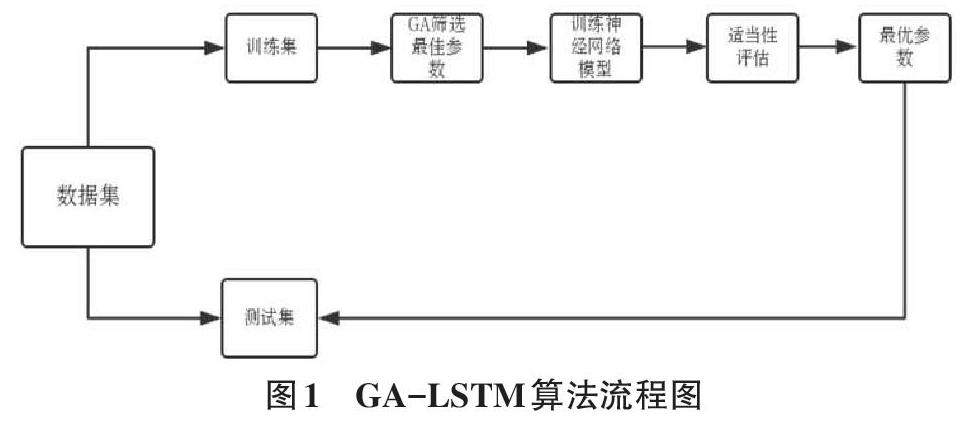
期货数据作为一种金融时序数据,具有复杂的非线性、不稳定性等特点,传统时间序列模型针对这类数据建模效果往往不尽人意。长短期记忆模型作为一种基于深度学习的神经网络算法可以在处理此类数据时发挥优势。本文在LSTM神经网络模型的基础上,融合遗传算法对模型参数进行优化,从而得出最优解,建立模型,對期货价格进行预测。具体算法流程如图1所示。
寻找最佳窗口及单元数方法大致分为以下四个步骤:
步骤1、解码遗传算法解决方案以获得窗口大小和单元数。
步骤2、使用GA找到的窗口大小来准备数据集,并将其划分为训练和验证集。
步骤3、输入LSTM模型,在验证集上计算RMSE,并返回该值将其作为当前遗传算法解决方案的适应度值,得出最优参数。
步骤4、建立LSTM神经网络模型,并使用上述步骤得出的最优时间窗口大小及最优神经网络隐藏层单元数作为相应参数并预测结果。
本文中使用的染色体编码为二进制位,表示时间窗的大小和LSTM神经单元数。随机生成初始种群,使用伯努利分布随机初始化。根据适应度函数和选择进行评估,然后进行交叉和变异,使用有序交叉、随机突变和赌轮选择。这个过程重复定义迭代的次数中重复。最后,选择一个具有最高适应度分数的解决方案作为最佳解决方案。适应度函数是遗传算法的重要组成部分,必须慎重选择。在本文中我们使用RMSE(均方根误差)来计算每个染色体的适应度,并返回最小的RMSE子集作为最优解,得到最佳窗宽及单元数目。
3实证分析
3.1数据准备
本文选取螺纹钢期货作为研究对象,数据通过上海期货交易所平台获得。在本文中,选取收盘价为输出变量。输入变量除开盘价、收盘价、最高价、最低价以及持仓量外,将一些技术指标也考虑在内,如MACD、KDJ、ROC等。技术指标主要分为趋势型指标:MA、MACD等;反趋势型指标:KDJ、RSI、ROC等;以及人气型指标:PSY等。由于输入变量较多,而各变量之间存在信息重叠,较多的输入变量也会降低LSTM神经网络的收敛速度以及预测精度。因此,我们应用主成分分析法(PcA)对输入变量进行降维,保留原始的开盘价、收盘价、最高价、最低价,针对其他指标进行降维处理,最后保留七个输入变量。
首先,由于期货交易并不是每天都进行,因此需要对缺失值进行处理,本文为简化过程,选择将却是数据行直接删除。接下来将数据进行归一化处理,消除数据不同量纲的影响,同时提高预测精度。在归一化处理时我们选择sldearn下的Min-MaxScaler函数,将数据归一化至0到1之间。
3.2模型预测及结果分析
本实验均在Python语言下编程,深度学习模型使用tensor-flow下的keras完成,遗传算法应用DEAP包完成。将数据处理完成后,本文采用以下四个步骤进行建模:
步骤1、确定输入层及输出层。通过遗传算法挑选最优窗宽,将处理好的七维数据对应窗宽作为输入变量,本文中训练出的最优窗宽为9。换句话说,也就是在预测一个收盘价数据时,我们需要用到过去九天的数据。输出层为预测收盘价的连续数据。
步骤2、设置网络参数。本实验设定隐藏层数目为一层,隐藏层神经网络单元数按照遗传算法训练出的最优单元数14个设定,激活函数选用默认的Sigmoid函数,隐藏层到输出层的激活函数选用Linear线性函数,LSTM神经网络使用Adam作为优化函数,MSE作为损失函数。
步骤3、计算预测误差。本文中使用均方根误差(RMSE)计算预测值与真实值之间的误差:
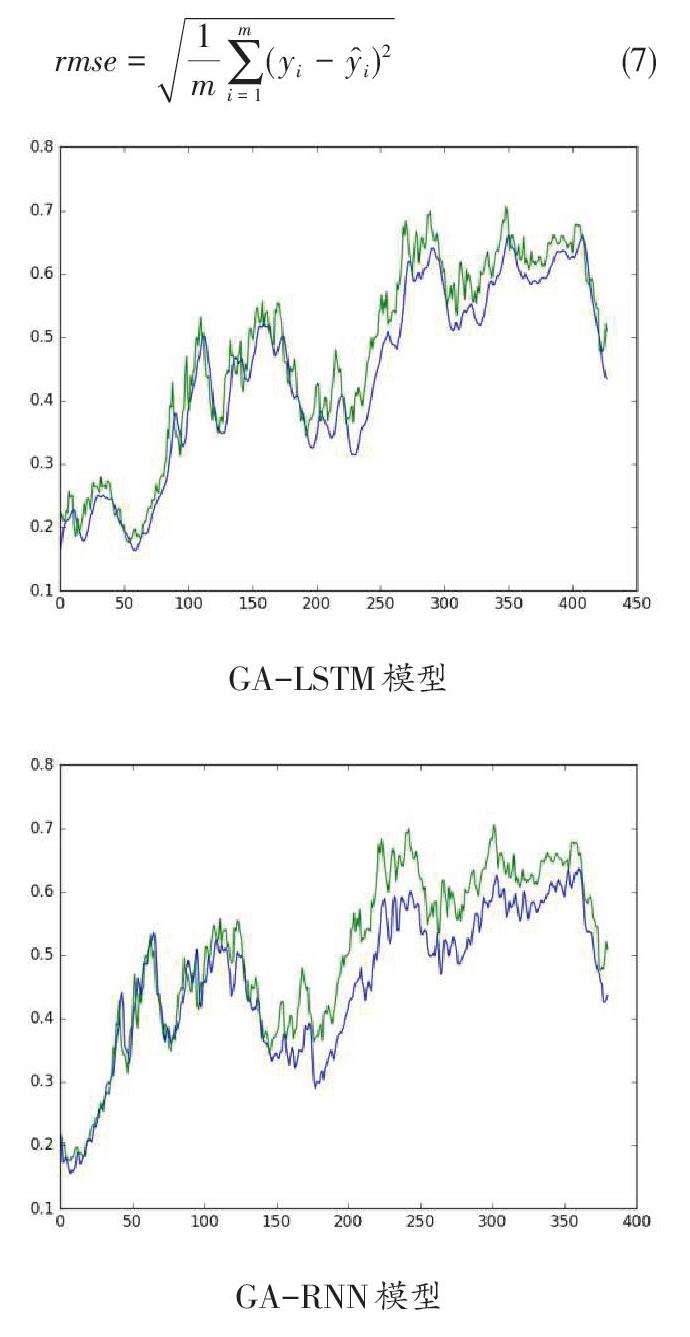
本文选取上海螺纹钢期货2009年3月30日至2018年4月4日的交易数据,共2196条作为实验样本,其中80%作为训练集,20%作为测试集。经过前期数据处理,计算技术指标,进行主成份分析,将得到的数据输入构建的GA-LSTM模型。本文为验证实验结果,将设置GA-RNN模型、LSTM模型、RNN模型作为对照组。实验结果如下图2所示。
其中,绿色线为测试数据的收盘价真实值,蓝色线为不同模型的收盘价预测值。从上图可以粗略看出遗传算法改进的RNN及LSTM模型都较原模型拟合效果好,GA-LSTM模型的预测值更贴近于真实值,较GA-RNN模型更为准确。为了更清晰的评价各模型预测精度,计算各模型的均方根误差进行对比。各个模型的均方根误差值如表1所示。
在建立传统LSTM神经网络及RNN神经网络模型时,本文根据多次实验及经验选取适当的参数进行建模,由于时间等因素限制并不能保证参数为最优。从实验结果可以得出结论,GA-LSTM神经网络具有良好的预测效果,模型拟合效果最好,均方根误差最小,并在有限时间内找出了最佳窗宽及最优神经网络隐藏层单元数目,多次实验结果也较为稳定,可以看出此改进方法有效。
4结论
针对具有时间序列特征的期货价格预测问题,本文创新地提出了GA-LSTM模型,应用遗传算法对长短时记忆神经网络模型进行优化,找出最佳时间窗口大小及神经网络隐藏层单元数目的参数,以得到最佳预测结果。本文选取螺纹钢期货作为实验数据,通过对比实验验证了该模型的可行性,并取得了良好的预测结果,提高了预测精度。該模型在时间序列数据的研究中将有更广阔的应用前景。

