基于图论的卢浮宫博物馆人员疏散模型的构建与分析
陈铭锟

摘要:近年来,大型博物馆紧急事故频发,如何以一种合理、快速的疏散计划来应对显得极为重要。因此,本文以卢浮宫博物馆为模型,根据其各通道路线的信息,以及人在逃离时的平均安全速度,基于图论构建了最短路径网络流模型。做出适当假设,根据Ford-Fulkerson算法以及最大流最小割定理,求解出逃离卢浮宫的最大人流量和具体最佳逃生路线,并建立最大流量网络流模型。根据通道优先级评估该模型,并在最后提出了将该模型推广到其他大型建筑的方法。
关键词:Ford-Fulkerson算法;最大流最小割定理;最佳逃生路线;最大流网络模型
中图分类号:TP391 文献标识码:A
文章编号:1009-3044(2020)01-0172-02
1问题提出
以卢浮宫博物馆为代表的大型人流密集场所,具有规模大、访问量大、建筑结构拥堵等。因此,如何构建一种可行的,能应对多种情况的具体逃生模型是首要问题。同时,该模型还需要满足能在最短时间逃生,能提前预测不同突发情况并实时调整逃生路线。
2问题分析
为简化问题,本文分成以下五个部分来分析:
1)基于建筑图,做出合理假设,构建最优逃生路径的数学模型;
2)计算出全部游客撤离所需的时间;
3)如何选择能达到最大人流量的逃生路径;
4)提出如何实施模型以及如何推广到其他大型的拥挤结构。
3模型建立与求解
3.1最优逃生路径的数学模型
本文将卢浮宫的逃生路径的定义为集合G(M,L),其中N为所有节点的集合,A为路径的集合,o为逃生出口节点,每一条路径(i,j)∈L消耗的逃生时间为tO,FS(i)为从节点i出发的所有路径的集合,IS(i)为到达节点i的所有路径的集合,如果路径(i,j)∈L,则xij=1,否则xij=0。最优逃生路径的数学模型可以表达为:
最优逃生路径的选择可分为路径最短寻优和时间最短寻优,对后者用Ford-Fulkerson算法以及最大流最小割定理求得最佳疏散时间,提出疏散方案,开发紧急疏散模型。为了得到合理的路网权值,可通过卢浮宫建筑图构造CAD模型,实地采集道路信息,分析建筑中的人群密度、道路结构分布并记录每条道路的各种信息。
3.2模型的分析和结论
将CAD图转化为最大流网络图,通过相应算法可得单位时间人流量,同时将每一段人流量转换成其对应的疏散时间。疏散时间最短是衡量应急疏散最优路径的指标之一,每条路線的权值即为通过该路线的所需时间tij。当疏散人数较多时,人在集结点(即网络图中的源点)的等待时间会比较长,因此下面考虑人在源点的等待时间(此处假设源点为A,汇点为a,b,c):
3.3 Ford-Fullkers伽算法求解最大流的数学模型
主要思想即在流量守恒的约束下寻找增广链,当无法获得增广链时算法终止,其正确性依赖于这个定理:当残存网络中不存在一条从s到t的增广路径,那么该图已经达到最大流。本文通过Matlab计算每个节点与卢浮宫疏散的最终出口f即节点16)得出卢浮宫疏散模型中不至于超过逃跑道路能容纳的人流量,即最大流。
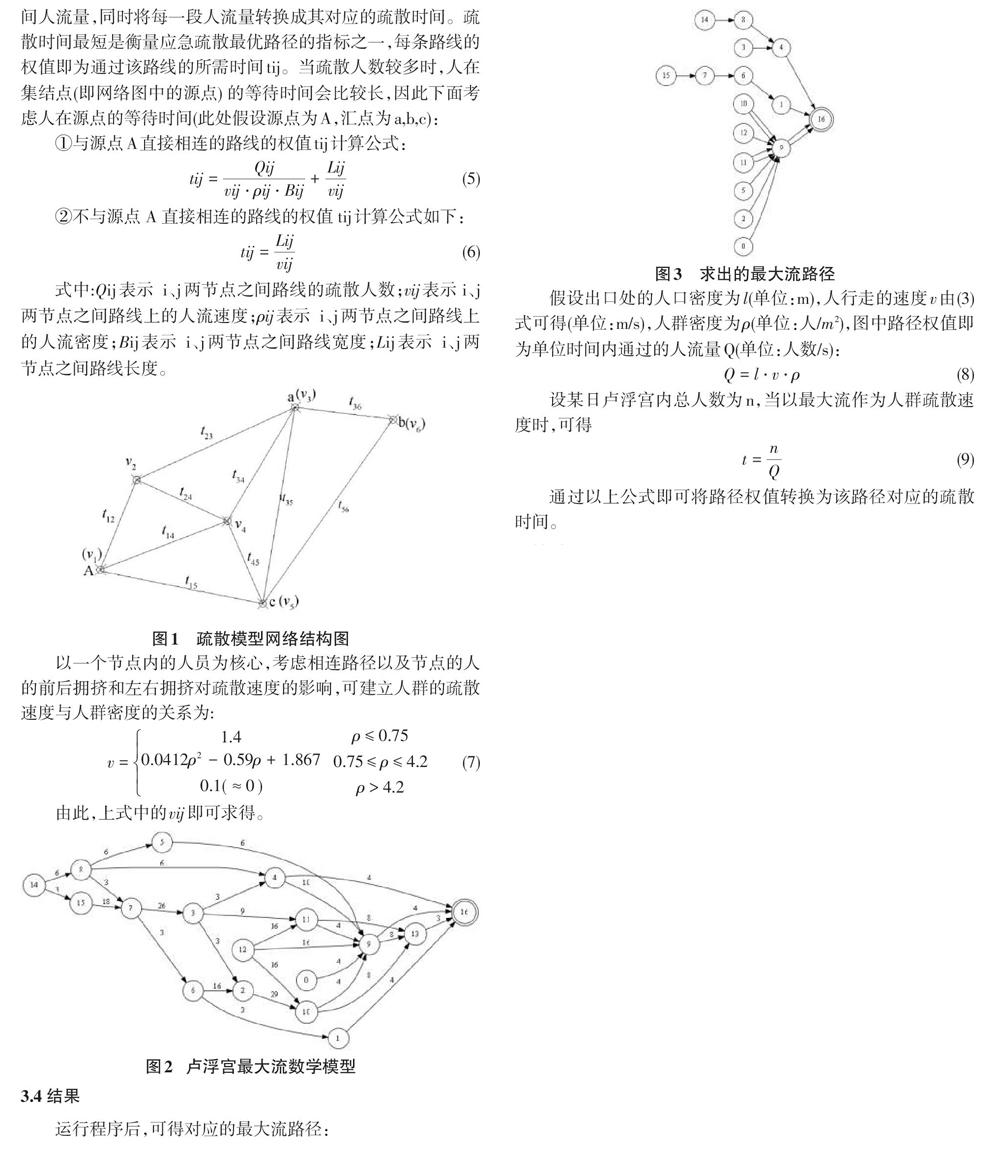
3.4结果
运行程序后,可得对应的最大流路径:
4结论
本模型充分考虑了人员安全疏散时的突发情况,并对可能出现的突发情况对模型提出了方便的优化的办法。当紧急通道的优先级大于通往公共出口的通道优先级时,开启紧急通道并将紧急通道的疏散路线纳入原本的疏散模型中,重新运行算法即可。
此疏散通道的评估体系可以推广到其他大型场所:只需根据建筑物具体的信息,通过修改源点、弧和权值的具体数量和数值,以及通道和出口的数据,重新运行算法,便可得到最佳的逃亡路线。

