内置立柱对矩形TLD 固有频率的影响分析

黄鹏

(广州大学-淡江大学工程结构灾害与控制联合研究中心）

1 CFD 分析TLD 模型的理论原理

TLD 水箱内液体三维晃动问题可以由Navier-Stok es 方程和连续性方程来描述，并采用雷诺时均的湍流数值模拟（RANS）方法，其中Navier-Stokes 方程可用笛卡尔张量形式表示为：

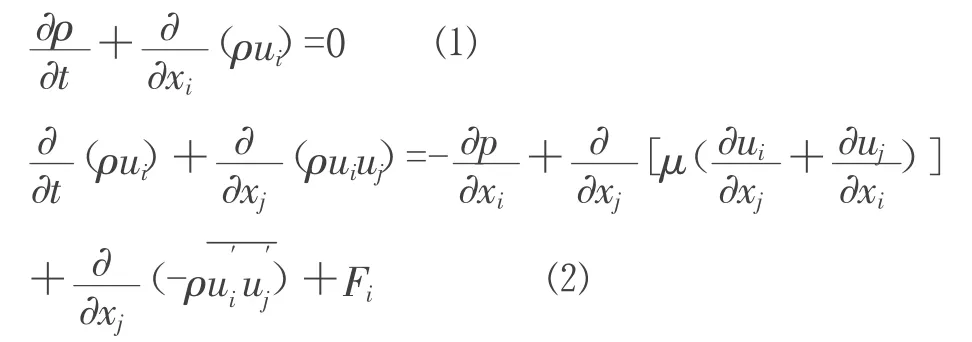
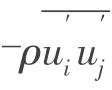
上述控制方程可以采用基于有限体积法的数值模拟算法来加以求解，本文利用Fluent 软件中基于多相流的基本模型，采用流体体积函数（Volume Of Fluid,VOF）方法捕获晃动液体的自由表面。VOF 方法被普遍采用来跟踪和捕获液体晃动问题中的自由表面。在VOF 方法中，流体（相）之间没有相互穿插，所有相的体积分数之和为1。在单元中, 如果第q 相流体的体积分数记为αq,则可能出现以下三个情况：

⑴αq=0：第q 相流体在单元中是空的。

⑵αq=1：第q 相流体在单元中是充满的。

⑶0＜αq＜1：单元中包含了第q 相流体和一相或者其他多相流体的界面。

2 模型算例

为了验证本文采用的基于多相流的基本模型CFD数值模拟方法，模拟内置立柱矩形TLD 系统中液体晃动特征的可行性，本文采用Love 等的内置立柱TLD 水箱振动台试验进行对比分析。试验水箱尺寸如图1 所示。

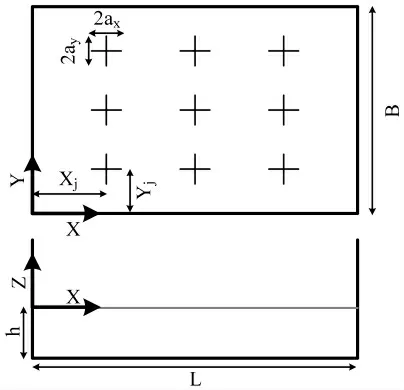
图1 水箱平面图及立面图

水箱的长宽高为L×B×H=889mm×785mm×785mm，水深h=133.35mm，立柱尺寸为ax×ay=117.75mm×117.75mm，且立柱中心点分别位于长和宽的1/4、1/2、3/4 倍距离位置处。试验在水箱底部施加单向水平正弦激励为：

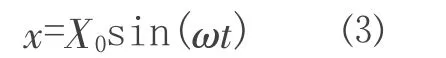
式⑶中：X0为位移激励幅值；ω 为外加激励对应的频率，TLD 系统对应的各阶固有频率为：

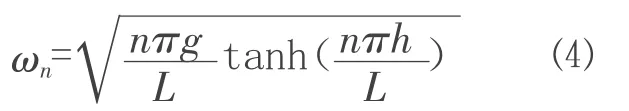
如式⑷中，n=1 则对应为TLD 系统的一阶晃动频率；g 为重力加速度，取9.8(m/s2)；h 为水深。

3 计算结果

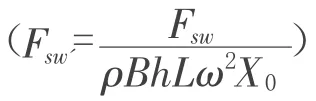
从图2 (a)- (b) 中可看到，在底部激励较小（X0/L=0.3%）时，侧壁波高和水平控制力随着激频比的增大而增大，在激频比达到0.92 左右时，侧壁波高和水平控制力达到最大值，随后随着激频比的增大，侧壁波高和水平控制力逐渐减小，可看到本文数值模拟的结果与试验结果较为一致，吻合精度较高。图2(c)(d)所示为侧壁波高幅值随激频比变化的数值模拟结果与试验结果在底部激励较大时（X0/L=0.6%）的对比。上述两图中可看到两种不同外激励幅值得出的数值模拟结果与试验结果基本一致，均在激频比达到0.92 左右时，侧壁波高和水平控制力达到最大值。由图2 中的各图可看到，本文所建立的CFD 数值模拟分析模型能较好地模拟内置立柱TLD 水箱液体晃动时所产生的水平控制力和侧壁波高，可以为高层及超高层建筑顶部安装有内置立柱TLD 水箱的振动控制效益分析提供参考。

4 结论

本文采用计算流体动力学（CFD）方法，对内置立柱的矩形TLD 水箱系统，在底部正弦位移激励时其中液体晃动的振动特征，建立了数值计算仿真分析模型，基于已有试验数据，验证了该模型及数值模拟技术的正确性，可以得到以下结论：

⑴通过与已有试验结果的对比分析，结果表明本文建立的基于有限体积法的CFD 数值仿真分析模型可较好地模拟内置立柱的矩形TLD 水箱在不同激频比作用下其中液体的晃动特性，能较好地预测箱内液体运动时的侧壁波高和水平控制力。

⑵通过对内置立柱TLD 的数值模拟研究发现，TLD系统在外激励与固有频率相近时，将出现共振现象，侧壁波高和水平控制力达到最大值，出于工程经济的考虑，应使TLD 系统尽可能的出现共振，实现效益最大化。

图2 数值模拟结果与试验结果的对比

⑶内置立柱会导致TLD 固有频率发生变化。本文算例中内置立柱导致TLD 的固有频率减小约8%。为了让TLD 系统发挥出其最大的减振效果，在调谐TLD 系统频率应考虑内置立柱对其固有频率的影响。