物理解题中的极限思维运用

叶志素

(江苏省连云港市灌云县下车中学 222231)

一、伽利略的“理想实验”

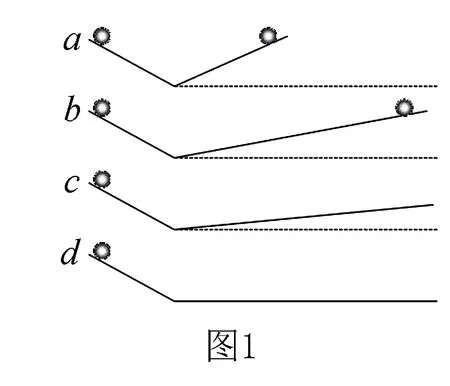
伽利略在实验中发现，若让小球从一定的高度无初速度释放，那么另一端的挡板与水平面的夹角越小，则小球运动的越远，若忽略摩擦和空气的阻力，小球将总能沿着光滑的斜面到达原来的高度.此时伽利略便思考，随着第二个斜面倾角的逐渐减小，小球也将运动的越来越远，如果继续减小第二个斜面的倾角直至水平，那么小球将再也达不到原来的高度，会以恒定的速度永远运动下去.至此，伽利略在理想实验的前提下，利用极限思维的方式得到了“力不是维持运动的原因” 的结论，推翻了亚里斯多德维持了两千多年的错误观点，也为牛顿第一定律的提出奠定了坚实的基础.

二、初中物理解题中极限思维的应用

极限思维在初中阶段的解题中具有非常广泛的应用，灵活使用极限思维能够帮助我们快速解决某些难以入手的题目，但大多学生都不懂如何使用极限思维，笔者在此根据以下几道例题来向各位讲解.

1.密度或压强习题中极限思维的应用

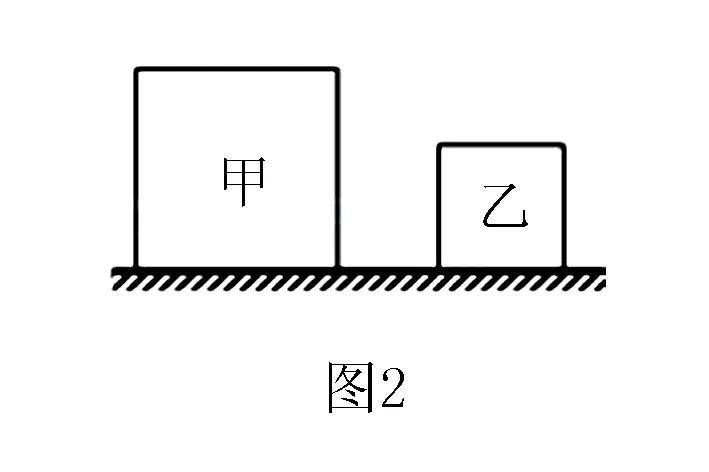
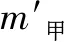
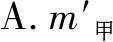
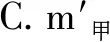
这道题要在甲乙两个物块截取相同的高度后的质量大小，对于初学者来说，读完题目后往往是无从下手，直觉上是认为原来相等，截取相同高度后，剩下部分也应该相等.但这样的思维是错误的，但作为老师如果用传统方法来给学生讲解，往往会因为繁复的推导过程使学生不知所措，但是利用极限思维便可以快速得找到突破点.由图2中可以看出甲物块比乙物块要高，我们可以一次性将乙物块全部切掉，而甲物块还有剩余，那么显而易见，是甲物块剩余部分的质量更大一点，故选择D项.这样的方法是不是既简单又直观？

2.运动学习题中极限思维的应用

例2 现AB两地间有一条河流，A地处于上游.河流上有甲乙两个休息点，甲在A地，乙在B地，现有一只船以速度v从甲休息站开往乙休息站，到达乙休息站后，立刻返回甲休息站，往返一次的时间为t，如果甲乙之间的距离为s，则下列选项中正确的是( )

A.t>2svB.t=2svC.t<2svD.以上情况均有可能

此题若要采取传统方法来解答，要对往返两种情况进行讨论，难以避免繁复的推导过程，且作为一道选择题会浪费过多的时间，极限思维在此处就有了用武之地.此题涉及了三个物理量：路程，船速和水流速度.我们选择将水流速度极大化，让水流速度与船速相等.当船逆流返回时，此时的合速度为0，则船将永远无法返回，即时间会无限大，所以此题的答案为A.

3.电学习题中极限思维的应用

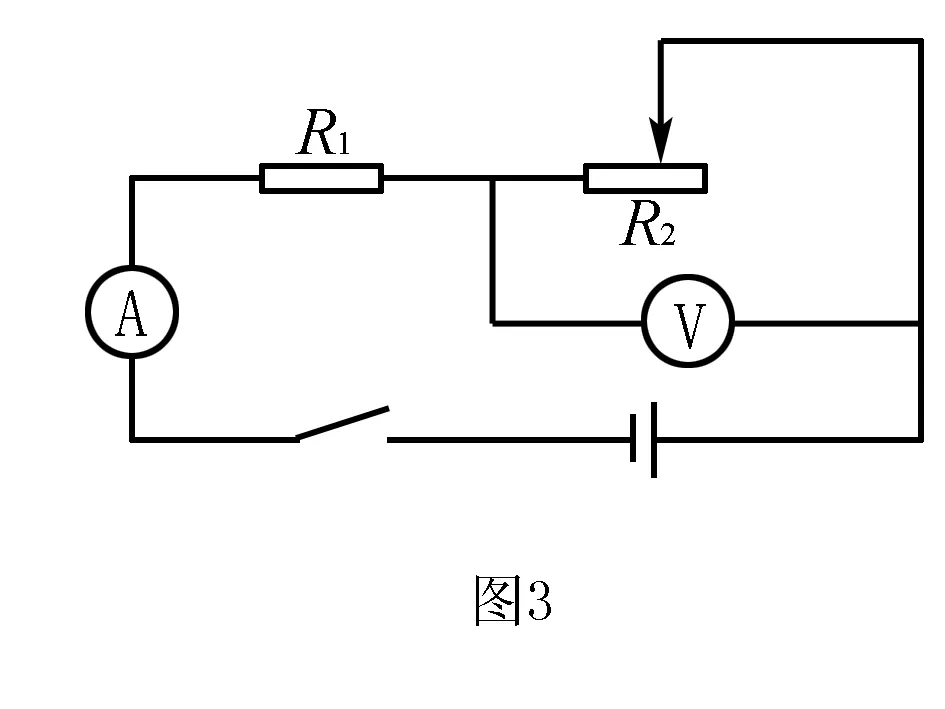
例3如图3所示，电源电压为12V，R1为定值电阻，滑动变阻器R2的变化范围为0～20Ω，如果电流表的量程为0～0.6A，电压表的量程为0～3V，为了不使两表损坏，求电阻R1的最小值.

在考虑电学问题时，情况往往会比较复杂，要充分结合电路图的实际情况，搞清楚串并联并画出等效电路.若电路要求我们求解某些电阻的取值范围或者电表的适用区间，我们就可以使用极限思想对某些值进行处理.

此题设定了电压表和电流表的量程，也就是有了两个限制条件.由题目中电路图可知，R1和R2是串联电路，利用极限的思维很容易想到：当滑动变阻器R2的阻值为0时，电路中的总电阻最小，此时此时电流表的示数达到最大，为了让电流表不超量程，根据欧姆定律可得电阻R1的阻值最小应为20Ω.而当滑动变阻器R2的阻值达到最大(20Ω)时，电压表的示数达到最大，此时应该保护电压表若，R1的阻值应为60Ω.综上所述，为保护两个电表，R1的阻值最小应该为60Ω.

三、如何学会使用极限思维？

在上述例题的讲解中，相信大家可以看到利用极限思维是一种非常灵活的思维方法，能够解决多种物理问题，并且具有极高的解题速率.

在初高中物理中有很多地方是可以使用极限思维的，对老师来说，在教学过程中可通过结合相关例题将传统方法与极限思维进行对比，一方面利用传统的方法来训练学生的推理以及逻辑能力，另一方面利用极限思维来培养学生的跳跃性思考能力，在两个思维层面来加深学生对于题型的理解，对于学生是有极大的帮助的；作为学生，我们要对每一种题型进行多角度的思考，判断题干中的变量是否是连续变化，利用多种题型来训练常见的极限思维方法，必要的时候需要请教老师，在思维成型后便可以敏捷地解决一些使用传统方法难以解决的题型，大大地提高了解题速率，为考试“争分夺秒”.

极限思维虽然非常巧妙，但我们也不能顾此失彼，传统方法所训练的基础推理以及逻辑能力才是我们在物理学习中稳步前行的保障.