例谈一线三等角模型的建立与应用

邹艺宣

(福建省漳州市华安一中 363800)

一、模型呈现

如图1，点A、E、C在同一条直线上，已知∠1=∠2=∠3=α，其中α角可以是任意的角，可以是锐角、直角或钝角，都有结论：△ABE≌△CED.

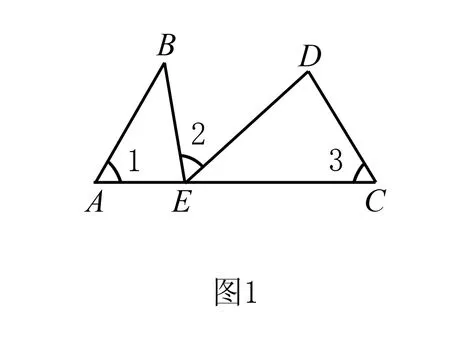
证明因为∠1=∠2=∠3=α，所以∠B+∠AEB=180°-α，∠DEC+∠AEB=180°-α,所以∠DEC=∠B，又∠1=∠3，所以△ABE≌△CED.

这个基本模型的特征是有三个相等的角，且三个角的顶点在同一条直线上，则它们的边所构成的两个三角形会始终相似.我们把这个基本图形称为一线三等角模型.

二、模型应用

1.显性模型，直接应用

例1如图2，在△ABC中，AB=AC=5,BC=8,点P是BC上的一个动点(不与点B、C重合)，连结AP，作∠APQ=∠B，PQ交AC于点Q.

(1)若BP=2,求CQ的长；

(2)若BP=x,CQ=y,求y关于x的函数关系式，并求出当BP为何值时CQ取得最大值.

分析第(1)问题目所给条件很明显已经具备一线三等角模型的特征，所以熟悉这个模型就可以快速联想到可以用相似来解题，可以提高解题的速度.第(2)问是要求由动点产生的最值问题，这是初中生的一个难点，但是第(2)的解答可以从第(1)题获得启发，两题之间是有联系的，只是把数字换成了字母，所用的方法是一样的，还是由一线三等角模型可以得到三角形相似，利用对应边成比例就可以得到y和x的函数关系式，再利用函数知识即可求出最大值.

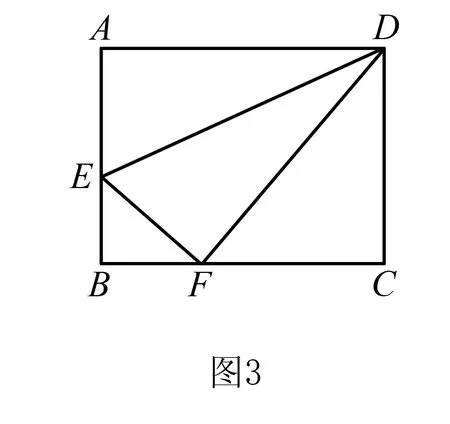
例2如图3，矩形ABCD中，AB=8,AD=10.点E是AB边上一点，把△ADE沿直线DE翻折，使点A恰好落在BC边上的点F处，则DE=.

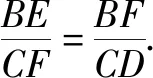
2.隐性模型，构造转化

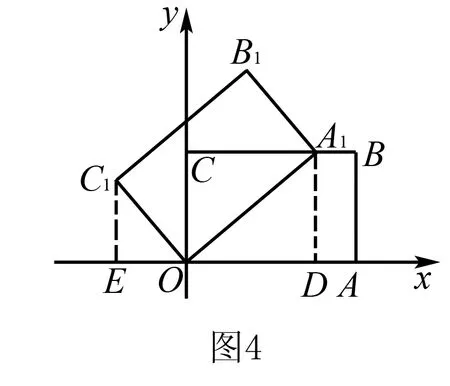
例3如图4，矩形OABC的两边OA,OC分别在x轴和y轴上，并且OA=5，OC=3若把矩形OABC绕着O点逆时针旋转，使点A恰好落在BC边上的A1处，则点C的对应点C1的坐标为( )

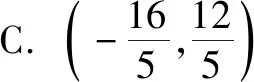
分析本题乍一看条件没有满足一线三等角模型的特征，但要求点的坐标，常添加的辅助线是过所求点C1作坐标轴的垂线，所以过点C1作C1E⊥x于点E，则会发现∠C1EO=∠C1OA1=90°.联想到一线三垂直模型，只要再过点A1作A1D⊥x于点D，则很快就可以找到解题的突破口.由△C1EO∽△ODA1得出答案为A.

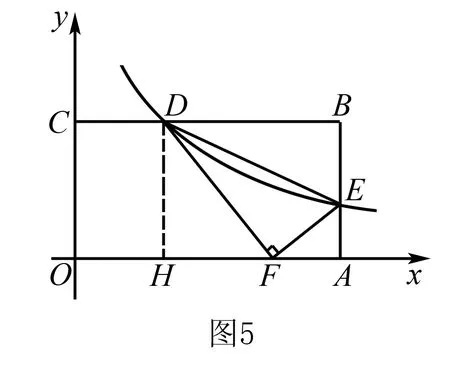
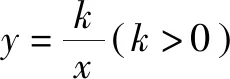
分析本题乍看不符合一线三等角模型，但时如果注意到∠DFE=∠OAB=90°,已经有点模型的影子，只要过点D作DH⊥OA于点H，则马上构造出一线三等角模型，快速找到解题的突破口.

在解决数学问题时，“如何找到解题的突破口”是很多学生较为困惑的.很多学生解题时没有思路和方向，而基本模型的提炼学习，可以帮助学生在众多的数学问题中找到具有共性的模型，这样可以为学生解题提供准确的解题思路和线索，还可以提高学生的数学核心素养.