基于粗糙集的矩形件优化填充排样方法研究

苗志民，盛步云，萧 筝，罗 军

（武汉理工大学机电工程学院&湖北省数字制造重点实验室，湖北 武汉 430070）

1 引言

矩形件优化填充排样是在备选的大量工件中选取合适规格的一系列工件，根据实际的工况条件，以最优的方式将其填满空白区域，获得最能满足设计意图的排样结果。在实际工作中，设计者基本采用手工试算或凭经验的方式进行排样，又需要综合考虑工件成本、加工与施工难易程度、企业偏好程度等诸多因素，造成排样困难、效率低下。目前，国内外学者在这方面进行了广泛的研究工作。文献[1]为解决矩形排样问题，采用不同启发式排样算法进行多目标优化，以求解最优布局；文献[2]针对矩形填充排样面积最小化问题，通过约束包络矩形的长宽比和制定内部填充策略，以提高最终布局的填充率；文献[3]通过动态约简填充排样问题的包络维数，将备选件对结果的负面影响定义为损伤程度，采用一种最小损伤优先法以求解最优布局问题；文献[4]研究基于属性重要度的优化填充排样算法，在考虑工件价格、颜色、花式的因素下，以材料利用率最高为目标进行优化排样；文献[5]建立了二维正交矩形布局问题的数学模型，利用图形矩阵化理论搜寻空白平面，通过动态填充启发式算法求解最优布局方式。上述研究中提出了一系列解决矩形排样问题的最优化方法，提高了排样效率与排样质量，但对工件价值的计算比较简单，大部分仅考虑了工件面积与材料利用率，而在填充排样中需要填满空白区域，排样的工件总面积是一定的。因此，在排样的过程中，矩形件价值的计算需要综合考虑工件成本、加工时间、施工效率和设计偏好度等诸多因素，以更好地满足设计人员的设计意图。针对矩形件优化填充排样问题，综合考虑价值评定因素，提出一种基于粗糙集理论的矩形件综合价值计算方法，建立优化填充排样模型，采用动态规划原理求解最优排样方式，并成功应用于系统开发，很好地解决了企业产品设计中的优化填充排样问题。

2 基本问题

2.1 排样问题描述

已知一待排样空白区域，工件系列共有r种，第i种工件的尺寸为li×wi（1≤i≤r），综合考虑价值评定因素情况下，计算综合价值为vi，对各类工件被选中的次数不做限制，排样的目标是在此区域排满的情况下，使得该区域所含工件总价值最大，并确定布置方式。

为满足实际的工况要求，工件的优化填充排样必须符合以下约束规则：

（1）相邻性，即同样型号规格的工件尽可能排布在一起，以缩短排样的工期；

（2）互不干涉性，即工件排布时需两两紧靠，且互不干涉，要求排满空白区域且不可超出；

（3）优先性，即后填入的工件不影响已填入区域工件的排布位置；

（4）统一性，即同一排样区域内工件排列方式保持同步，统一横排或统一纵排。

2.2 价值评定因素

排样工件尺寸的选择是由工件综合价值决定的。工件综合价值评定需要考虑的因素较多，这里选择工件成本、加工时间、施工效率和设计偏好度作为评价因素。

（1）工件成本：主要指材料成本，受工件的尺寸规格的影响较大；

（2）加工时间：主要考察加工的难易程度，以及对产品生产周期的影响；

（3）施工效率：工件生产完成后现场施工，施工安装的难易程度也作为评价的因素；

（4）设计偏好度：对于不同规格的工件其偏好程度不同，优先选用易于加工和施工的工件尺寸，节省成本。

2.3 排样相关概念

（1）段的分割。一个待排样的多边形空白区域称为段。已知待排的多边形的内角均为π/2或3π/2，称为排样多边形。排样过程中，需遍历排样多边形中内角为3π/2所对应的直角点，依次使用同方向的分割线将其划分为多个X向或Y向矩形子段区域，由于受到单个工件最大尺寸的限制，还需将子段区域进一步分割，段的水平分割和竖直分割示意图，如图1所示。

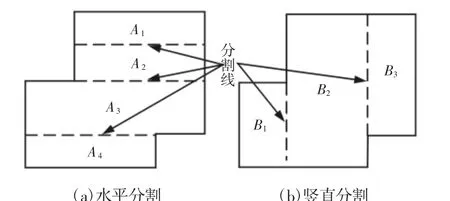
图1 段的分割图Fig.1 Segments Split Graph

（2）条带。一个或多个工件排列成一行（或列），称为条带。条带分为普通条带和同质条带，为了方便排样，采用同质条带，分为X向和Y向两种，如图2所示。

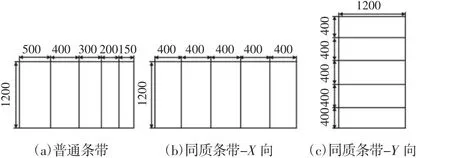
图2 条带图Fig.2 Bands Graph

（3）最优子段排样。对于排样多边形，将其分割成若干个X向或Y向子段，依次求解各子段的最优解以获得该区域的最大价值，排样方式，如图3所示。

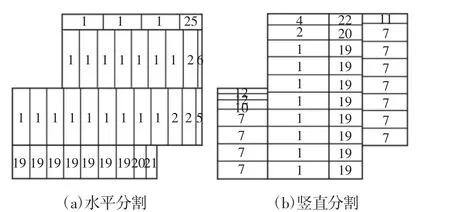
图3 排样方式图Fig.3 Nesting Mode Graph

3 基于粗糙集的矩形件优化填充排样模型

在排样过程中，备用可选的工件种类繁多，数量巨大，同时需要考虑诸多因素的影响，给决策带来困难。因此，实现优化排样的首要前提是工件综合价值vi的确定。粗糙集理论是用来处理不完整性和不确定性问题的有效数学手段[6]。通过粗糙集理论确定矩形件综合价值vi，为后续求解最优排样模型提供决策依据。

3.1 基于粗糙集的综合价值计算

设在排样过程中需考虑的决策因素为 E=（E1，E2，…，Em），决策属性为 F=（F1，F2，…，Fn），有如下定义：

定义1DS=是一个四元组的决策信息系统。其中，

U≠Ø为论域；

A≠Ø为属性集合，E为条件属性，F为决策属性，则有A=E∪F，E∩F=Ø；

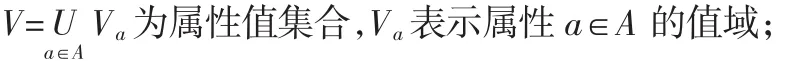
f：U×R→V为信息函数，R为U的一组等价关系，f映射U中每一对象的属性值。

（1）求F对E（k1≤k≤m）的依赖度 δE（kF）。δE（kF）表示DS根据的信息能够划分到等价类U/IND（E）的对象数占系统总对象数的比值，即：

式中：|*|—集合的基数。

（2）求条件属性Ek的重要度φEk与权重ωk。φEk表示从E去除Ek，计算其决策结果浮动的程度，浮动程度越大表示该属性所占权重越大。

（3）求矩形件的综合价值vi。vi指所有影响决策结果变化的Ek权重加权和。

3.2 矩形件优化填充排样模型

根据以上问题描述与工件综合价值的计算方法，建立矩形件优化填充排样模型。设排样多边形的最大价值为V，对于水平分割方式，分割成s个X向矩形子段，其总价值为VX，第k个子段尺寸为 xk×yk，ai为该子段中 xki×yk条带的个数。

则xki×y条带的价值：

第k个X向子段的价值：

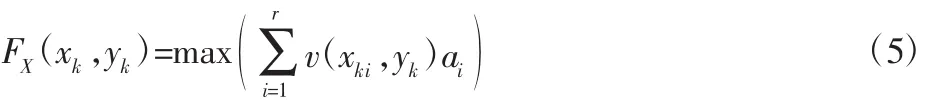
X向段的总价值：

对于竖直分割方式，分割成t个Y向矩形子段，其总价值为VY，第 k 个子段尺寸为 xk×yk，bi为该子段中 xk×yki条带的个数。

则 xk×yki条带的价值：

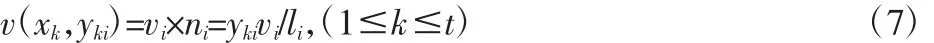
第k个Y向子段的价值：

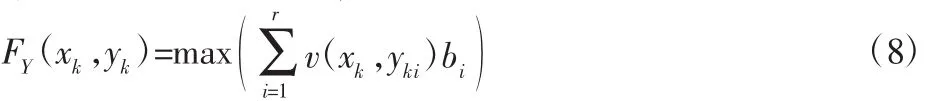
Y向段的总价值：

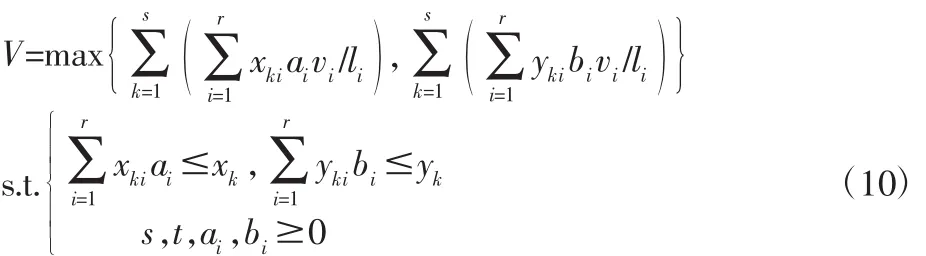
可见，该数学模型是背包问题[7-9]。下面将用动态规划原理求解，计算和最优布置方式。

3.3 基于最优子段排样的动态规划算法

动态规划算法的思路是将待求解的问题划分为多个相互联系的子问题，先求子问题的解，再通过子问题解来获得原问题解[10]。

设xmin、ymin为条带最小长度和宽度，Δx、Δy为长度和宽度方向的增量，生成X向最优子段xk×yk最大价值的动态递归式为：

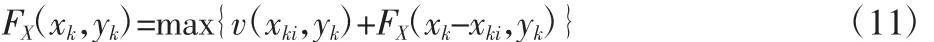
则基于最优子段的X向段最大价值动态规划算法，如图4所示。同理可求得Y向段全部可能尺寸的最大价值。

求解矩形件优化填充排样模型算法流程如下所示：

（1）输入排样多边形尺寸与工件数据；

（2）根据式（1）～式（3）将条件属性进行定量描述，依次计算决策属性表中的各矩形件的综合价值vi；

（3）根据式（4）、式（7）确定 X 向条带、Y 向条带的价值 v（xki，yk）、v（xk，yki）；

（4）运用动态规划算法分别求解式（10），计算排样多边形分别采用水平和竖直分割生成的最优子段排样总价值VX、VY；

（5）根据 VX、VY，计算排样模型最大价值 V=max（VX，VY），确定最优布置方式。

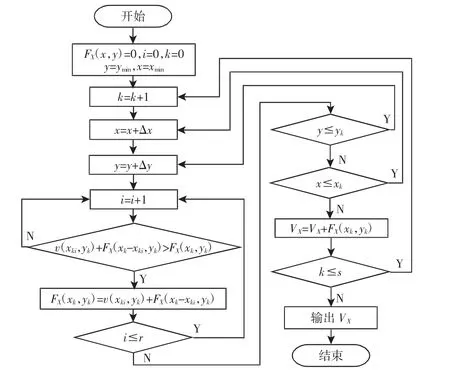
图4 基于最优子段的动态规划算法Fig.4 Dynamic Programming Algorithm Based on Optimal Sub Segments

4 应用实例

为验证上述方法的有效性，以国内某一建筑科技公司铝模板排模设计为例，基于C#语言开发铝模板智能排模设计系统，系统在SolidWorks平台上进行二次开发，所有排摸结果以3D模型格式输出。建筑楼面的形状大多为排样多边形，其配模模板有平面模板、支撑模板和角模板三部分。平面模板布置在矩形子段区域，支撑模板布置在段的分割线处，角模板布置在楼面边角位置，便于模板拆装与固定。在铝模板楼面排模设计过程中，由于支撑模板与角模板的尺寸、位置相对固定，故仅考虑平面模板的优化填充排样问题。已知，备选平面铝模板系列共有123种，由于研究铝模板在楼板平面内的排样问题，故仅需考虑其长宽尺寸，铝模板的标准尺寸规格，如表1所示。

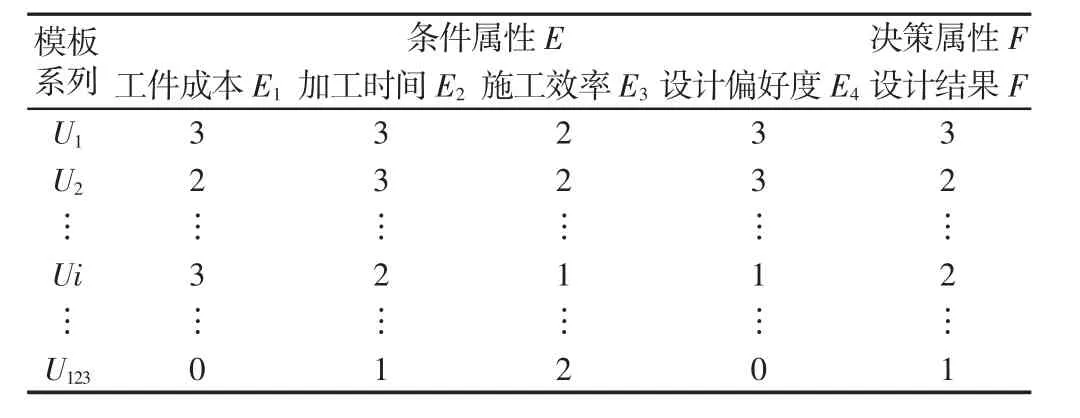
表2 决策属性表Tab.2 Decision Attribute Table

决策属性定性描述分为设计结果非常好（F1）、好（F2）、一般（F3）、不好（F4）四个值，记为F=（F1，F2，F3，F4），且F1=3，F2=2，F3=1，F4=0；决策因素有工件成本、加工时间、施工效率和设计偏好度，故条件属性分别记为E1、E2、E3、E4，其对应的定量描述分别为非常重要（3）、重要（2）、一般（1）、不重要（0），由企业铝模板设计规则与评价指标，依次得出E1～E4和F的决策属性值，如表2所示。根据决策属性表和式（1）～式（3）计算各模板的综合价值，其计算过程如下：

表1 铝模板尺寸规格Tab.1 Aluminum Formwork Size

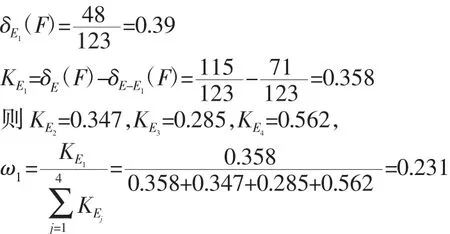
同理可求得ω2=0.223，ω3=0.184，ω4=0.362。

由式（4）得：

同理可求其余模板综合价值，其常见规格模板的综合价值，如表3所示。随机选取3个待排样的楼面区域，根据基于粗糙集理论的矩形件优化填充排样模型，利用基于最优子段排样的动态规划算法求解结果，如表4所示。X向段与Y向段排样结果，如图5所示。结果表明，1号区域和3号区域Y向段排样模板种类少，标准模板较多，易于统计和施工，且VXVY，故选用X向段排样方式。

表3 常见规格铝模板综合价值表Tab.3 Comprehensive Value of Common Aluminum Formwork

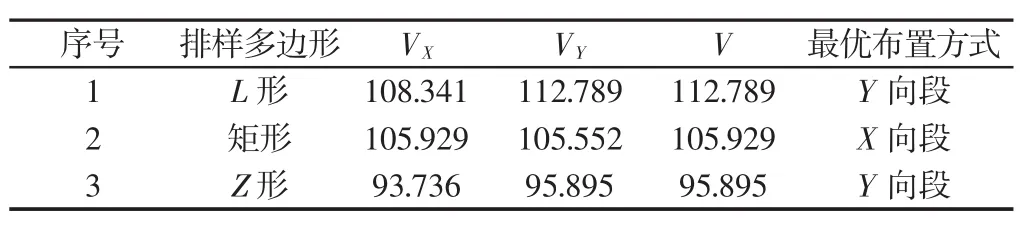
表4 排样结果表Tab.4 Nesting Result

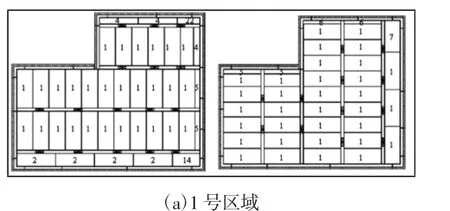
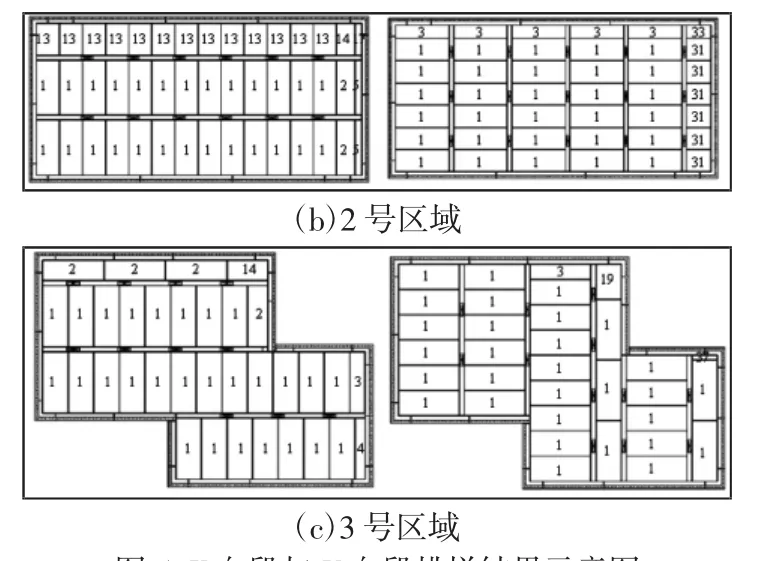
图5 X向段与Y向段排样结果示意图Fig.5 Nesting Result of X and Y Segements

5 结束语

将工件成本、加工时间、施工效率和设计偏好度作为矩形件综合价值的评定因素，提出一种基于粗糙集理论的矩形件综合价值计算方法，建立矩形件优化填充数学模型，将排样多边形划分为多个矩形子段，采用基于最优子段的动态规划算法计算出排样最大价值，确定最优布置方案，切实提高了企业产品设计中大规模排样的效率与质量。对于异形区域与异形工件的排样问题将是下一步主要研究的工作。