基于改进的U-Net生成对抗网络的图像翻译算法*
常 佳,王玉德,吉燕妮
(曲阜师范大学,山东 曲阜 273165)
0 引 言
图像翻译是将源域的输入图像向着目标域的输出图像转换的过程[1],是图像处理的一个重要领域。图像翻译(Image-to-Image Translation)广泛应用在计算机视觉任务中,如模糊图像修复[2-3]、人脸上妆[4]、图像上色[5]、图像生成[6]以及风格迁移[7]等。
Hertzmann等人首次提出了图像翻译模糊的概念[8],采用的是输入-输出图像对来训练一个非参数模型,然后利用这个模型训练输入的图像对应的输出图像,从而完成图像翻译。2014年Goodfellow等人受博弈论的启发[9],提出了生成对抗网络GAN。模型由生成器和判别器组成,生成器生成一个与真实图像类似的生成图像来迷惑判别器,判别器努力区分生成图像和真实图像。该模型利用对抗的思想实现了无监督图像翻译。Mirza等人提出了CGAN[10],在GAN生成器的输入中加入一个条件,将无监督图像翻译变成有监督图像翻译,从而可以按照人们的需要生成图像,实现图像翻译。Isola等人提出Pix2Pix[1],模型结构和CGAN一致,并且在损失函数中加入了L1损失,而生成器采用U-Net模型[11],大大提高了图像翻译的质量。
针对Pix2Pix生成的图像部分纹理、轮廓丢失以及噪声大等不足,提出了基于改进U-Net模型生成对抗网络的图像翻译算法。该算法重点解决的问题是生成器中反卷积层中信息强度的增强,通过生成器反卷积跳跃连接过程中逐次增加encoder重复次数来增强图像特征,从而提升图像翻译效果。
1 基本理论
2014年Goodfellow等人提出了生成对抗网络,基于二人零和博弈思想(两人的利益之和为零,即若一个人得到利益,则另一个人便失去利益),近年来已经成为深度学习比较热门的研究方向[12-13]。
GAN的模型包括两个部分——生成器(Generator,简称G)和判别器(Discriminator,简称D)。在训练过程中,生成器主要是生成一个与真实图片相似的图片;判别器的主要作用是判断输入图像是真实的还是生成的,输出结果是一个概率。若为真实图像,则输出为1;若是生成图像,则输出为0。生成器和判别器相互博弈,直到输出的概率为0.5时,判别器无法判别真假,模型达到最优。GAN的网络模型如图1所示。
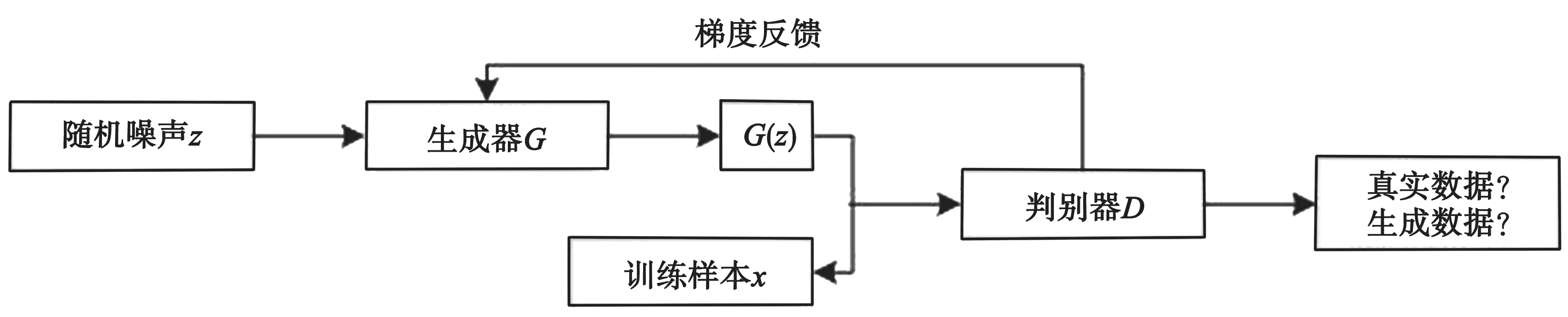
图1 生成对抗网络模型
GAN的优化函数为:
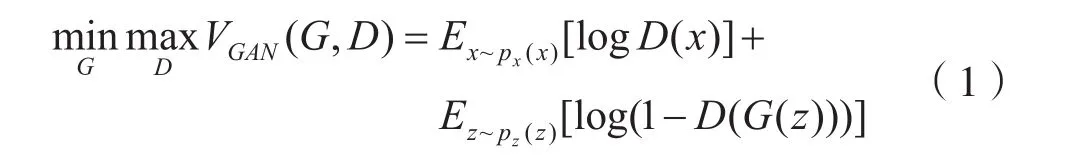
其中输入图像x服从px(x)分布,生成器的输入噪声z服从pz(x)分布。
实践中,GAN在训练过程中容易出现振荡而达不到均衡,出现部分模式崩溃现象,使得生成样本缺乏多样性。针对这一问题,Mirza等人提出了CGAN,期望网络根据输入条件生成指定的图像。与原始GAN不同的是,它在生成器的输入部分增加了条件约束,将无监督学习转换成有监督学习,其中加入的约束条件记为y,引导噪声生成图像模拟目标图像。CGAN的目标函数为:

其中,y是约束条件。
模型结构如图2所示。

图2 条件生成对抗网络模型
图像翻译质量是否提高是人们最关心的问题,常用的对图像翻译质量的评价指标分为主观评价和客观评价[14-15]。
主观评价采用的是用户调研方法,用户用肉眼直接观察图像翻译的质量。用户主观评价满意度指标用公式表示为:

其中A代表参加调研的人数,B表示从数据集中随机挑选的测试图像,N代表用户观察的最优的图像个数。
2 U-Net模型及其改进方法
2.1 U-Net模型结构
在神经网络中,浅层卷积核提取Low-Level特征,深层卷积核需要提取High-Level特征,从而尽可能保留更多的图像细节。Encoder-decoder只学习高级特征而丢失了低级特征,使得图像翻译的效果比较模糊,而U-Net模型可以同时学习高级、低级特征,将第i层拼接到第n-i层。这是因为第i层和第n-i层的图像大小是一致的,可以认为它们承载着类似的信息。这样就把浅层的特征通过channel维度跳跃连接到深层特征。Encoder-decoder和U-Net模型如图3和图4所示。
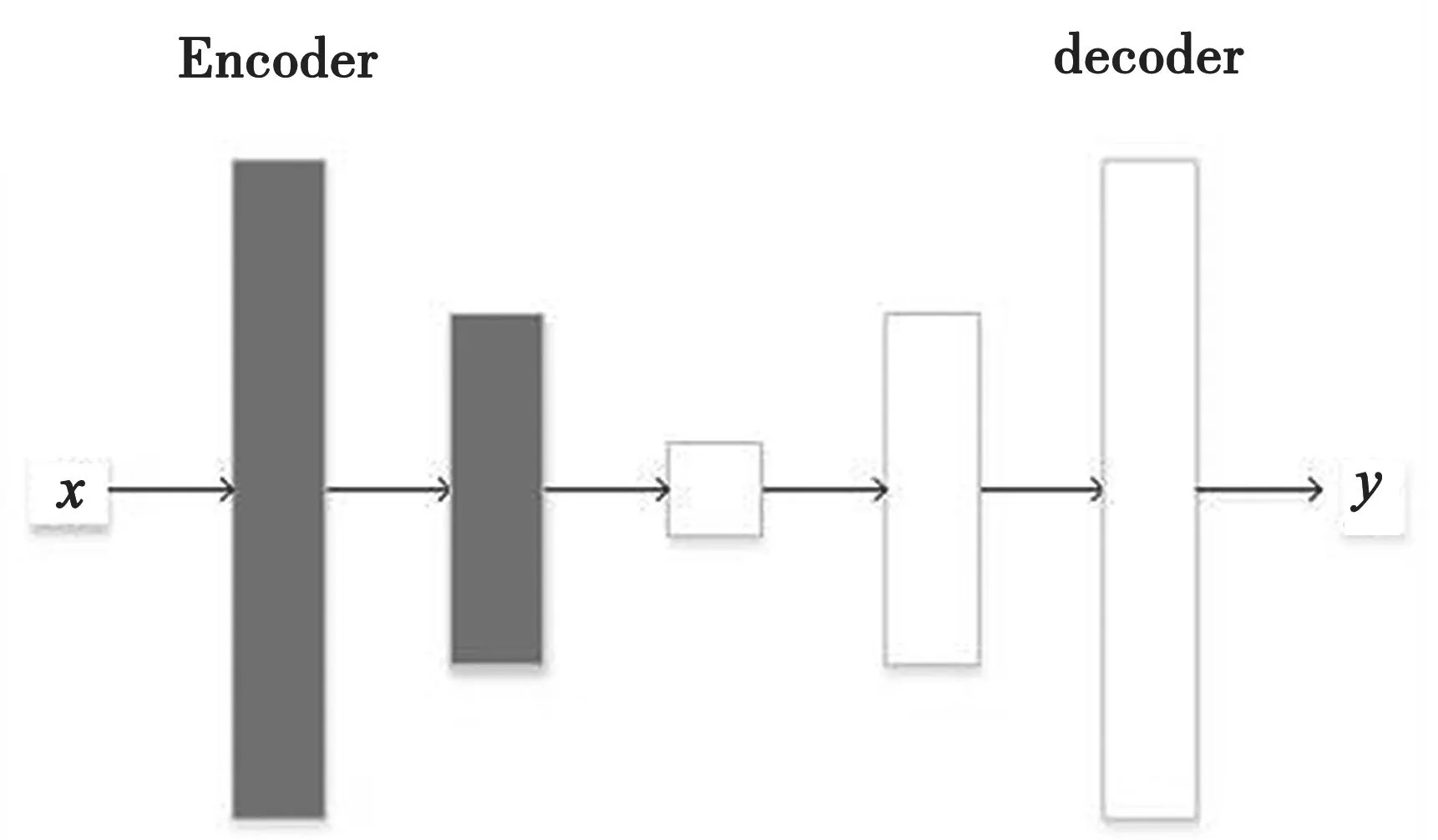
图3 Encoder-decoder

图4 U-Net模型
2.2 U-Net模型改进
U-Net模型第i层和第n-i层承载着类似的信息,通过跳跃连接就可以将第i层的特征复制到第n-i层,使得生成图像越接近于真实图像。但是,只做一次跳跃连接容易丢失图像纹理、轮廓等特征。为了增强图像特征表达能力,提高图像翻译效果,本文通过增加卷积层和反卷积层之间跳跃连接的次数来改进U-Net模型。改进的U-Net模型结构如图5所示。
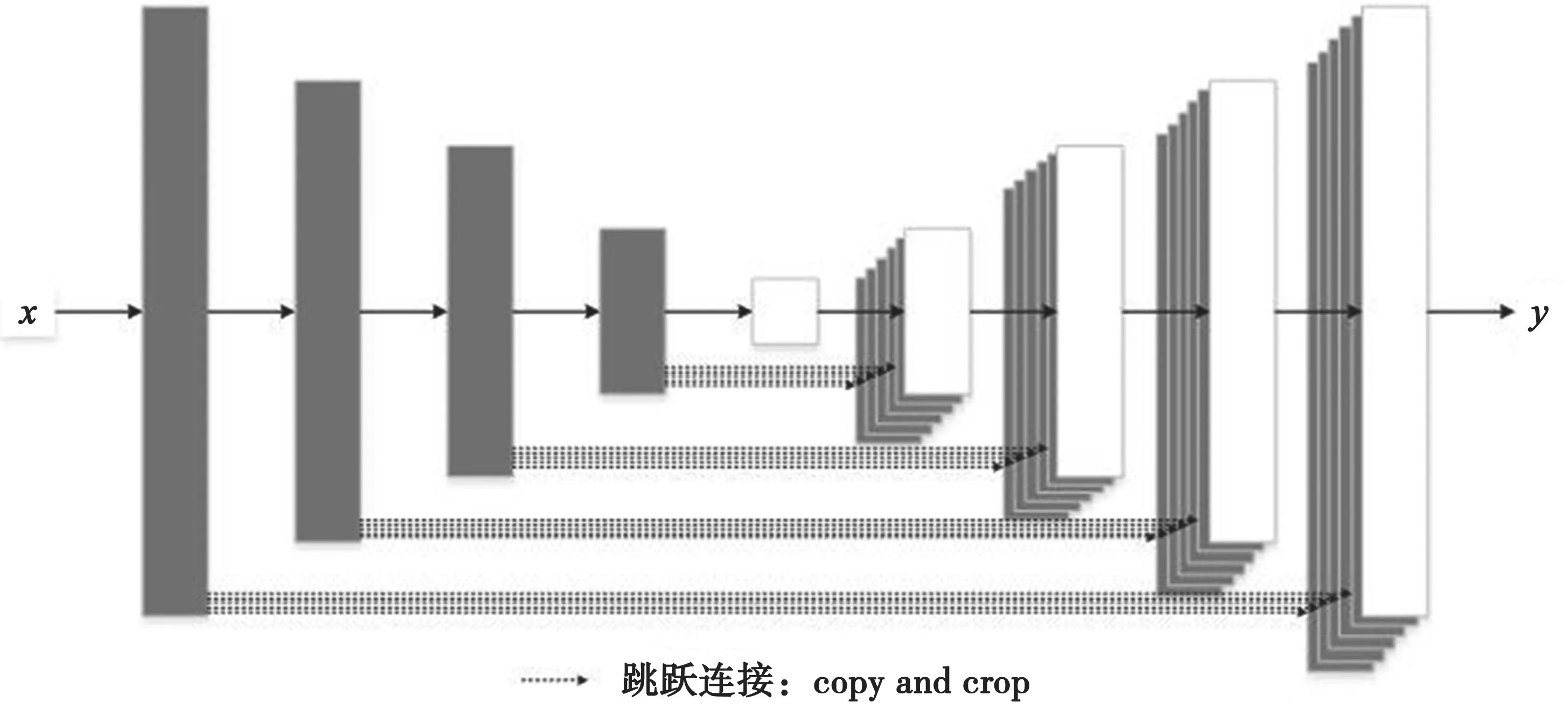
图5 改进的U-Net模型结构
生成器采用改进的U-Net模型,输入图像依次经过conv、激活函数和Maxpooling,然后将输出图像依次经过deconv、正则化、激活函数和dropout层,最后将图片大小相同的输出进行concat跳跃连接。生成器如图6所示。
判别器,是将真实图像和生成图像(或目标图像)进行concat(即预处理),得到的结果依次经过卷积、BN和激活函数层输出图像,然后经过扁平化和全连接层输出图片为真或者假的概率。判别器结构如图7所示。
3 图像翻译算法实现步骤
(1)对样本图像进行尺寸归一化处理,经过m个x×y(x可等于y)卷积核对输入的图片进行卷积操作,经过激活函数,选用n×n的池化单元完成下采样。
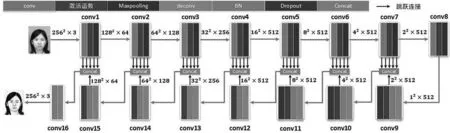
图6 生成器结构
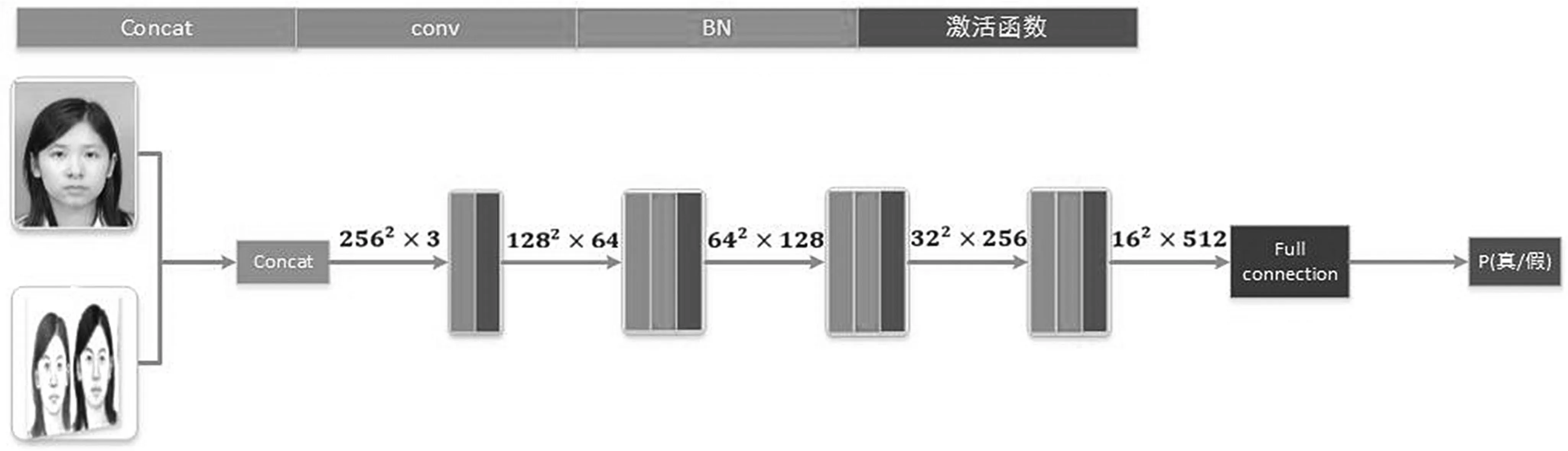
图7 判别器结构
(2)将encoder输出的结果进行反卷积、正则化和dropout操作。
(3)将encoder和decoder大小相同的输出进行concat操作,逐次经过卷积、BN和激活函数层,将输出的图像大小经过扁平化和全连接层,进而判断图像是真或假的概率。
(4)改变网络模型参数,优化算法,实验确定网络模型的最优参数。
(5)在步骤(4)的基础上,改变反卷积过程跳跃连接的重复次数,寻找最优反卷积过程跳跃连接次数的最优值,实现图像翻译。
4 实验与结果分析
本文选用的是CUHK人脸素描数据库里香港中文大学学生数据库,包括88张彩色图和88张素描图组成的训练集和100张彩色图和100张素描图组成的测试集。
实验条件为Intel(R) Core(TM) i5-4590 CPU@3.30 GHz,内存64 GB,Windows10操作系统,编程软件基于TensorFlow 1.10.0框架,python3.6.5。对图像进行预处理,模型卷积核为3×3,平均池化为2×2,步长为2,激活函数选择ReLU。
4.1 实验1
分别选用AdaGrad算法、RMSProp算法以及Adam算法等优化算法,实验迭代200次,实验观察算法对图像翻译质量的影响,结果如图8所示。
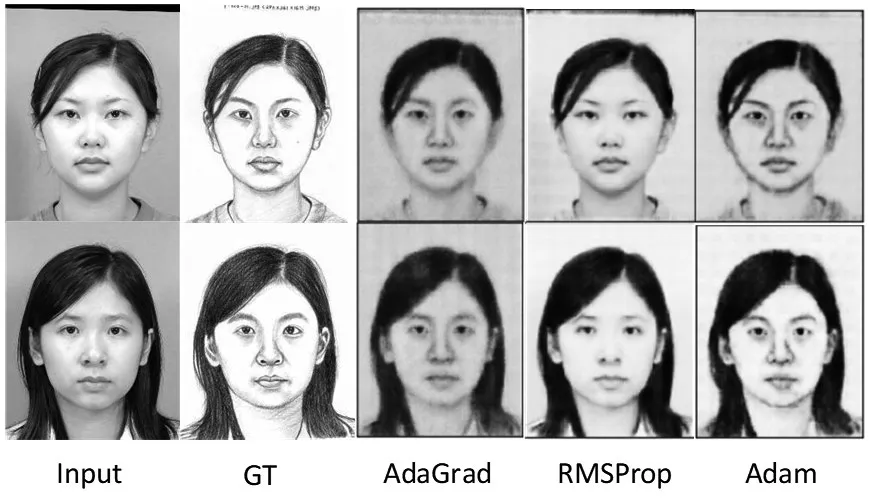
图8 不同优化算法翻译结果
从图8可知,当优化算法选择Adam时,翻译结果接近于GT图像,故选择Adam算法对实验进行优化。
4.2 实验2
优化算法选择Adam方法,改变网络模型学习率和迭代次数,研究网络模型参数对图像翻译质量的影响,实验确定模型参数。
研究网络模型中学习率、迭代次数等参数对改进后的图像翻译算法的影响,其中优化算法选择上面得出的Adam算法。
(1)迭代次数设定为200次,学习率分别设置为0.01、0.001、0.000 1,实验结果如图9所示。
从图9看出,学习率设置过大,生成的图像轮廓较为清晰,一些细节方面被遗弃;设置过小,噪声太大,会影响图像的轮廓。所以,学习率设置为0.001。
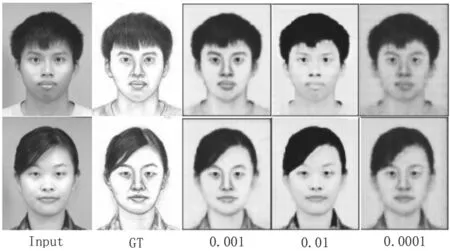
图9 不同学习率翻译结果
(2)学习率设为0.001,优化算法为Adam算法,改变网络迭代次数,实验结果如图10所示。

图10 不同迭代次数翻译结果
为了说明模型在不同迭代次数下生成图像的效果,列出不同迭代次数下生成器生成的图像、输入图像和目标图像进行对比。如图10所示,最左边是输入图像,最右边是目标图像,生成器生成的图像要向目标图像进行靠近,迷惑判别器。从图10可以看出,随着迭代次数的增加,生成器生成的图像在面部轮廓、纹理细节等方面越来越接近目标图像,同时背景噪声大幅度减少。
4.3 实验3
学习率设为0.001,迭代200次,优化算法为Adam算法,在U-Net模型的反卷积过程中逐渐增加concat跳跃连接的encoder重复次数。实验观察U-Net模型中反卷积跳跃连接encoder重复次数对图像翻译质量的影响,实验结果如图11~图16所示。
从图11可以看出,当选用原始模型时,生成器损失曲线从迭代2次时开始急剧下降到32万,之后在27万~32万之间来回震荡;迭代50次后,在23万~27万之间对抗,总体呈现下降趋势;判别器损失曲线在迭代3次时急剧下降到1.4,迭代25次左右时曲线损失增加到20,之后随着迭代次数的增加,曲线在1~7之间来回震荡,达成对抗。
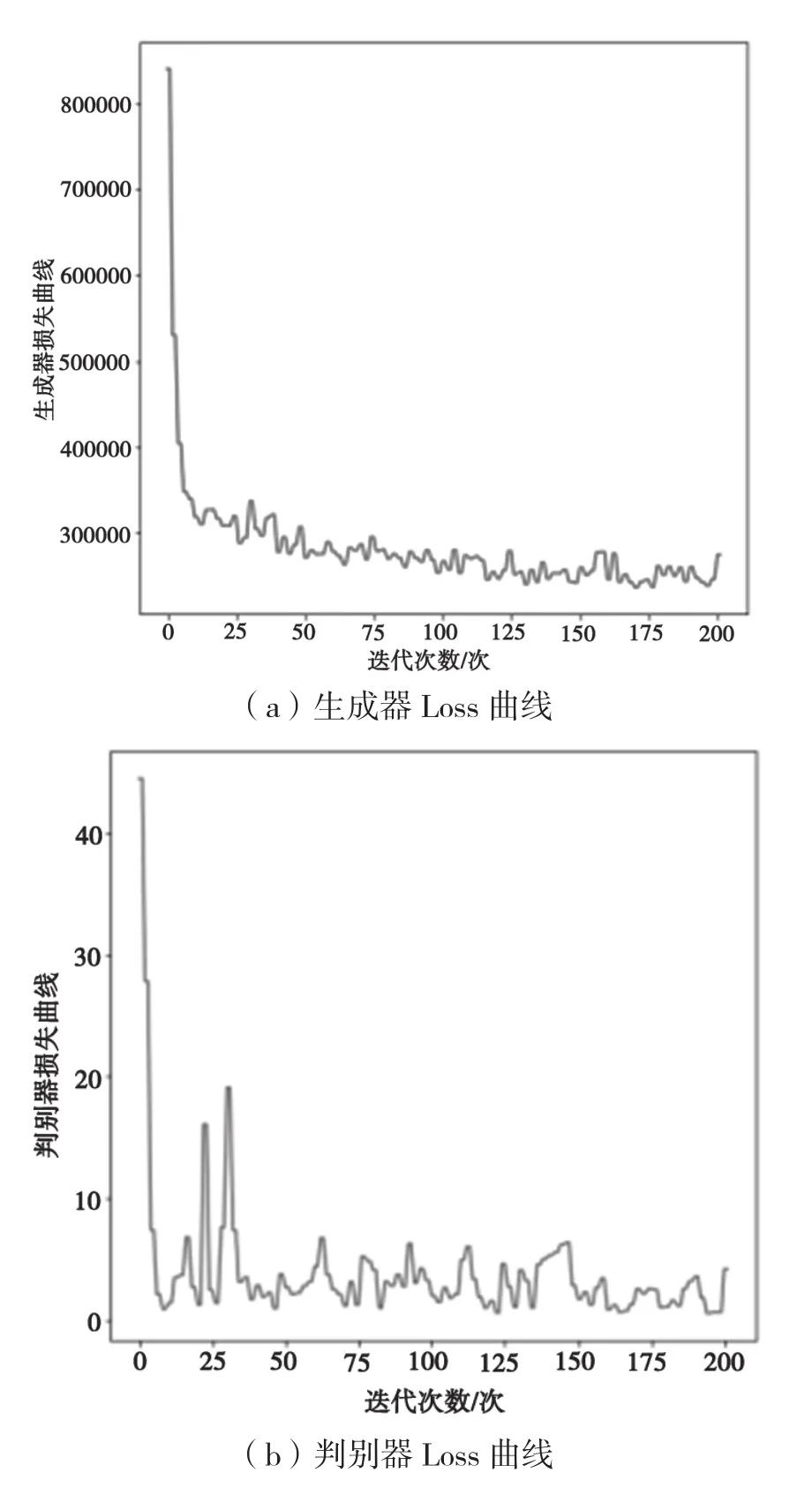
图11 原始模型Loss曲线
从图12可以看出,当跳跃连接encoder增加到2次时,生成器的损失函数曲线在迭代3次时急剧下降,然后随着迭代次数的增加损失在25万~28万之间来回震荡,达到对抗,总体呈现下降趋势;判别器损失曲线当迭代次数在50时急剧增加到40,之后在0~9之间震荡,不稳定。
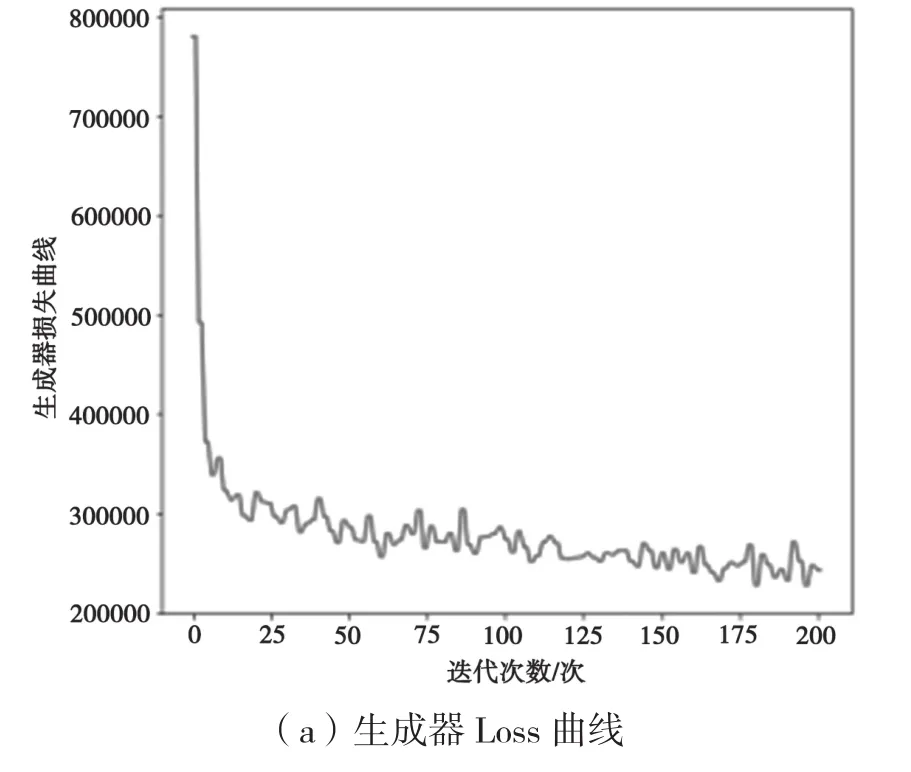

图12 跳跃连接encoder2次Loss曲线
从图13可以看出,当跳跃连接encoder增加到3次时,生成器的损失函数曲线在迭代3次时候急剧下降,然后随着迭代次数的增加损失在23万~33万之间来回震荡,达到对抗,总体趋势是收敛的;判别器损失曲线十分不稳定,迭代次数在50时急剧增加到43,之后在0~10之间震荡。

图13 跳跃连接encoder3次Loss曲线
从图14可以看出,当跳跃连接encoder增加到4次时,生成器的损失函数曲线在迭代3次时候急剧下降到35万,然后在2~50次时损失在20万~33万之间来回震荡,迭代次数在50之后震荡加剧;判别器损失曲线不稳定,迭代次数在50时急剧增加到60,之后在0~10之间震荡,迭代次数在75时急剧增加到58,对抗趋势较差。
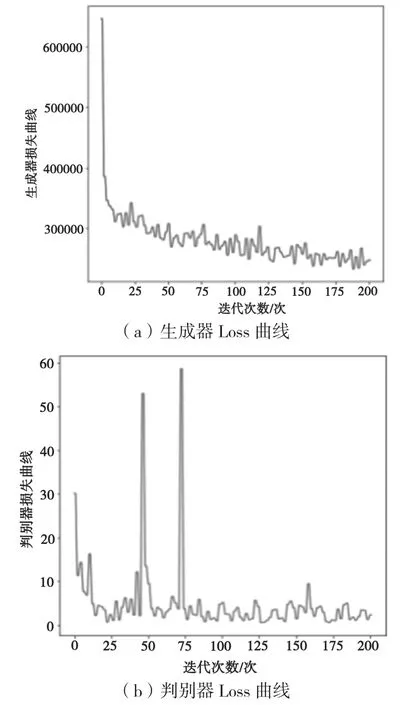
图14 跳跃连接encoder4次Loss曲线
从图15可以看出,当跳跃连接encoder增加到5次时,生成器的损失函数曲线在迭代3次时候急剧下降,然后随着迭代次数的增加损失在26万~33万之间来回震荡,达到对抗,总体趋势是收敛的;判别器损失曲线迭代次数在20时急剧增加,之后在0~8之间震荡,趋于稳定。
从图16可以看出,当跳跃连接encoder增加到6次时,生成器的损失函数曲线在迭代3次时候急剧下降,然后随着迭代次数的增加损失来回震荡加剧,未达到平衡;判别器损失曲线每隔50次急剧增加一次,十分不稳定。
encoder重复不同次数的生成图像,如图17所示。通过Loss曲线和生成的图像对比发现,当U-Net模型的concat层数encoder增加到5次时,图像翻译的效果最好。

图15 跳跃连接encoder5次Loss曲线
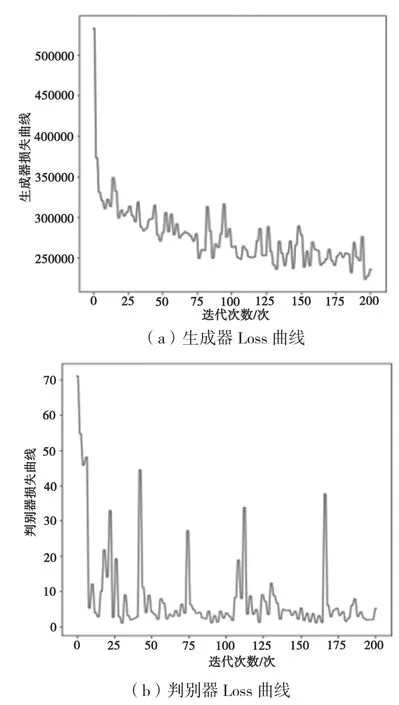
图16 跳跃连接encoder6次Loss曲线
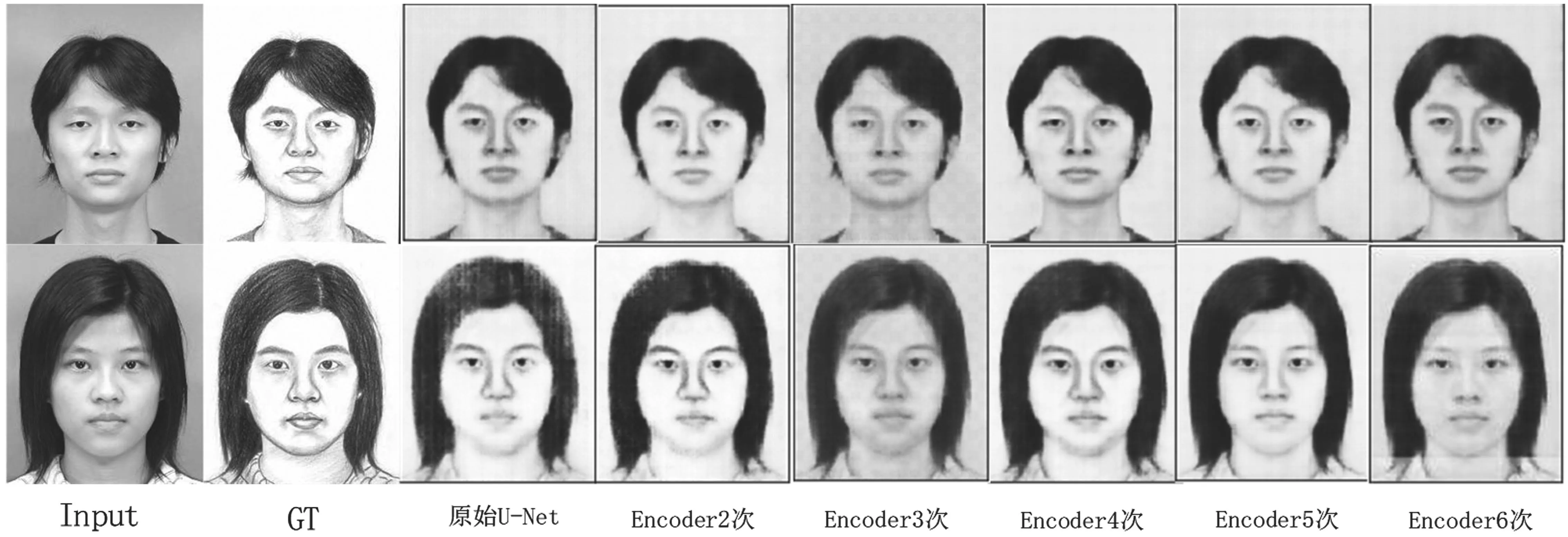
图17 encoder重复不同次数生成图像
实验选取不同跳跃连接encoder次数的图像翻译重复50次实验,图像翻译结果图像由专业人员、普通用户、学生100人对图像翻译结果进行评价,得出用户评价满意度指数。用户评价标准如表1所示,评价结果如表2所示。

表1 主观评价标准

表2 用户调研评价满意度指数
5 结 语
针对图像翻译质量问题,提出了一种基于改进U-Net模型的生成对抗网络图像翻译算法,主要通过增加反卷积过程跳跃连接中encoder的重复次数增强图像特征,得出了生成器反卷积跳跃连接重复次数为5时图像翻译的质量达到最好。论文研究结果可为图像翻译技术的实现提供理论支撑。

