永磁同步电机参数自整定及参数辨识技术研究

程 静，蔡华祥，陈 强，薛开昶

(1. 贵州装备制造职业学院，贵阳 550008；2. 贵州航天林泉电机有限公司，贵阳 550081；3．国家精密微特电机工程技术研究中心，贵阳 550081)

0 引 言

近十年来，永磁同步电机因其高控制精度高、响应速度快、功率密度大等特点使得它在交流伺服系统逐渐脱颖而出，并成为伺服系统执行机构应用的主流电机，其应用几乎遍及社会的各个领域，如高精度伺服转台、机器人系统、数控机床、医疗器械、自动化生产线等[1]。与此同时，随着技术的不断发展，各行各业的智能化水平都在不断提升，因此对永磁同步电机伺服系统也提出了更高的要求，主要体现在以下几个方面：①同步电机伺服驱动系统应具有自动识别电机参数的功能。②伺服驱动系统应具有随负载变化的自适应能力；③伺服系统具备控制器参数自整定、自调节的功能。基于此，本文主要从同步电机系统模型入手，分析伺服控制器参数整定的来源及依据，从而确定伺服控制所需的电机必要参数。并结合工程实际对必要参数进行辨识，使得控制器具有更广的适应性，降低控制器的调试时间，以及增加控制器的通用性[2]。

1 同步电机系统模型分析

为便于分析，建立同步电机数学模型前，通常需定义如下假设[3-4]：

①永磁材料的电导率为零。

②电动机定子绕组为三相Y型接法，三相绕组完全对称。

③相绕组中感应电动势波形是正弦的。

④铁磁部分磁路线性，不计饱和、剩磁、涡流、磁链损耗等影响。

⑤转子无阻尼绕组，永磁体无阻尼作用。

(1)

此时，电机同步电机运动学方程如下所示：

(2)

表贴式同步电机中，由于Lq≈Ld，进而有如下关系

(3)

式中,uq,ud分别为dq坐标下的q轴、d轴电枢电压分量；iq,id分别为dq坐标下的q轴、d轴电枢电流；Rs为电枢绕组电阻；ψq,ψd分别为dq坐标下定子磁链分量；φ为转子磁钢在定子绕组上的耦合磁链。Lq,Ld分别为dq坐标下的q轴、d轴等效电枢电感分量[5]；ωe=2πf·np为同步电机电角速度，f为定子电流频率。

对于表贴式同步电机而言，通常采用id=0的控制方式。依据上式可知，通过控制直轴电流iq就可以间接地控制同步电机电磁转矩，进而控制同步电机的转速。

若同步电机反电势为E,工程中通常取

(4)

式中,n为同步电机转速,r/min，kv为电机反电势常数，V/k r/min。

则还有如下关系：

(5)

式中，ke为国标规定的反电势常数值，(V/rad·s-1)，工程中常用kv来表示反电势常数。

根据国标GB/T 30549-2014的3.10规定，对于同步电机有

(6)

式中,kt为电机的转矩常数。

从而也有：

kv=60.46kt

(7)

2 控制器参数设计

如前所述同步电机的伺服控制模型如图1所示，模型包含位置环、速度环以及两个电流环(q轴电流环和d轴电流环)。由于表贴式同步电机通常采用id=0的控制方式，且两个电流环控制器参数可取相同的参数，因此通常同步电机多闭环伺服控制可以用图2所示的控制结构来简化。

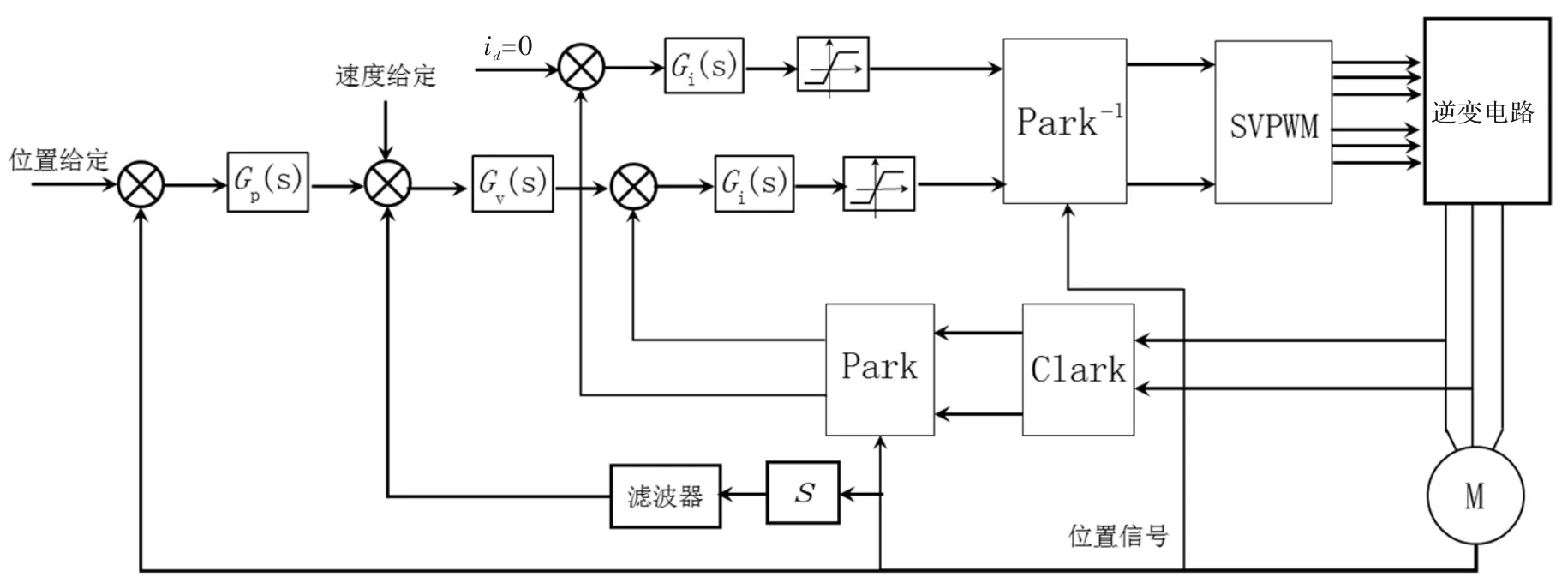
图1 同步电机伺服控制模型

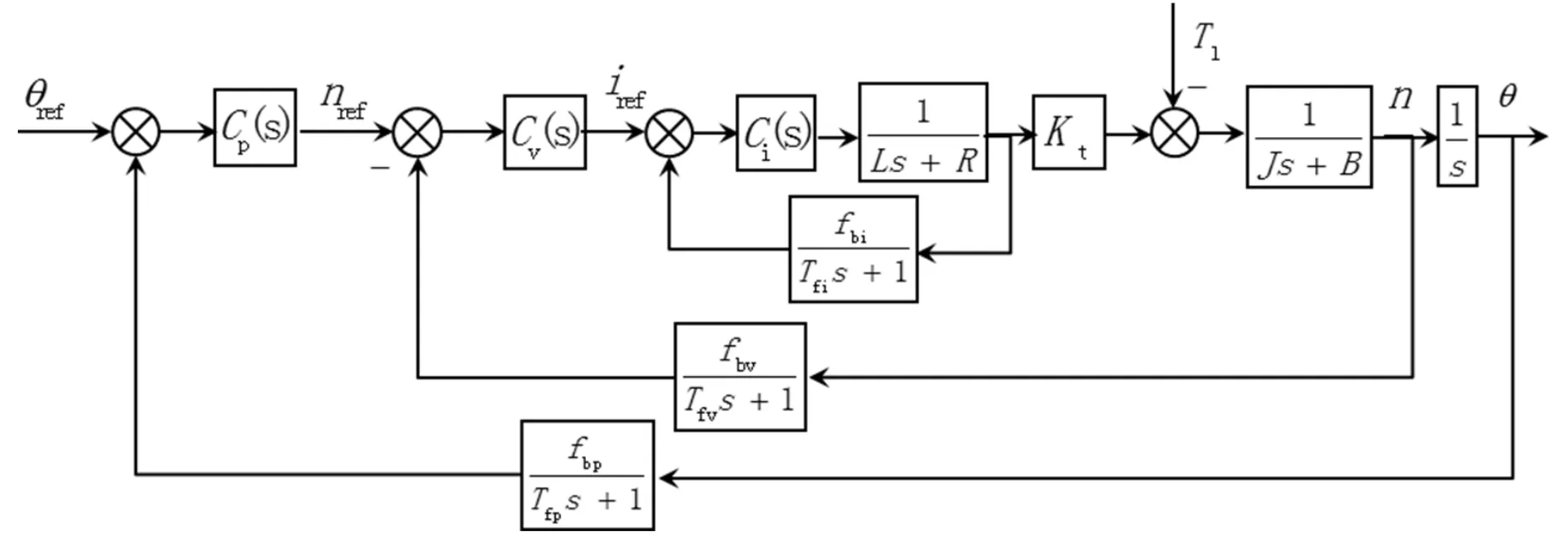
图2 同步电机简化控制结构

如图2所示，同步电机电流环开环传递函数可以用如下表达式来描述：

(8)

式中,Td为系统的延时时间常数，包含电流采样延时，电流环计算延时以及占空比更新延时等。但由于相比整个电流环中机电时间常数而言，Td值较小，该延时环节主要影响电流环高频特性，对电流环中、低频特性影响较小，甚至可忽略不计。故在设计电流环控制器参数时，通常不考虑延时环节，则有[6]

(9)

式中，ωcc为系统的开环截止频率。开环截止频率与系统闭环带宽关系为

ωcb=(1.1-1.4)ωcc

(10)

对于速度环，由于电流环闭环以后，输入电流近似等于输出电流，而根据前面分析可知输出电流与输出力矩呈线性关系

Te=ktiq

(11)

故速度环传递函数[7]如下

(12)

即

(13)

(14)

特别地，在工程应用中，由于阻尼系数B相比转动惯量其值非常小，导致其对速度环的影响很微弱，若仍按上述公式来计算速度环积分系数，将会导致速度环的稳态跟踪性能和抗干扰性能较差。因此，为保证转速无静差跟踪，工程中也常用下式来计算速度环的积分系数。

(15)

结合前面的分析可知，对于同步电机伺服控制器而言，若想实现控制器的参数自整定，则最少需要辨识几个参数：R、L、kt、J。

则速度环和电流环控制器参数可以依据所辨识的参数，设计为

(16)

3 参数辨识

3.1 电阻辨识

根据同步电机静止坐标系下定子电压方程，可知，当控制逆变器在定子两相之间施加小电压(如控制A相流入，B相流出)，同时给定一个确定的位置参考值，此时，电机将会在一个确定的位置保持静止不动，则可根据基尔霍夫电压定律可知，

(17)

式中，uab、iab分别为AB相之间的电压和电流稳态时，则有

uab=Udc=2Rsiab

(18)

从而可以知道同步电机电阻

(19)

需要注意的是，由于施加的电压值较小，因此必须要考虑以下几个问题：

①同步电机PWM死区压降Udead。

②逆变器单个场效应管压降Ufdmos。

③逆变器单个场效应管上续流二极管压降Ufkmos。

从而施加到定子绕组两端的电压计算公式如式(20)所示，式中D为PWM占空比。

因此，同步电机定子相电阻值可通过式(21)计算。

uab=(Udc-Ufdmos)·D-Udead-Ufkmos·(1-D)-Ufdmos

(20)

(21)

3.2 电感辨识

同步电机中电感主要对定子电流的瞬态变化有影响，因此可以用同步电机旋变坐标系下的定子电压方程来分析电机电感。

(22)

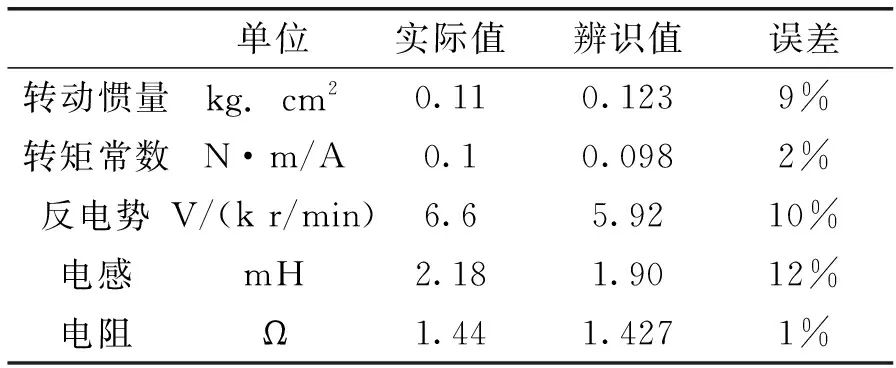
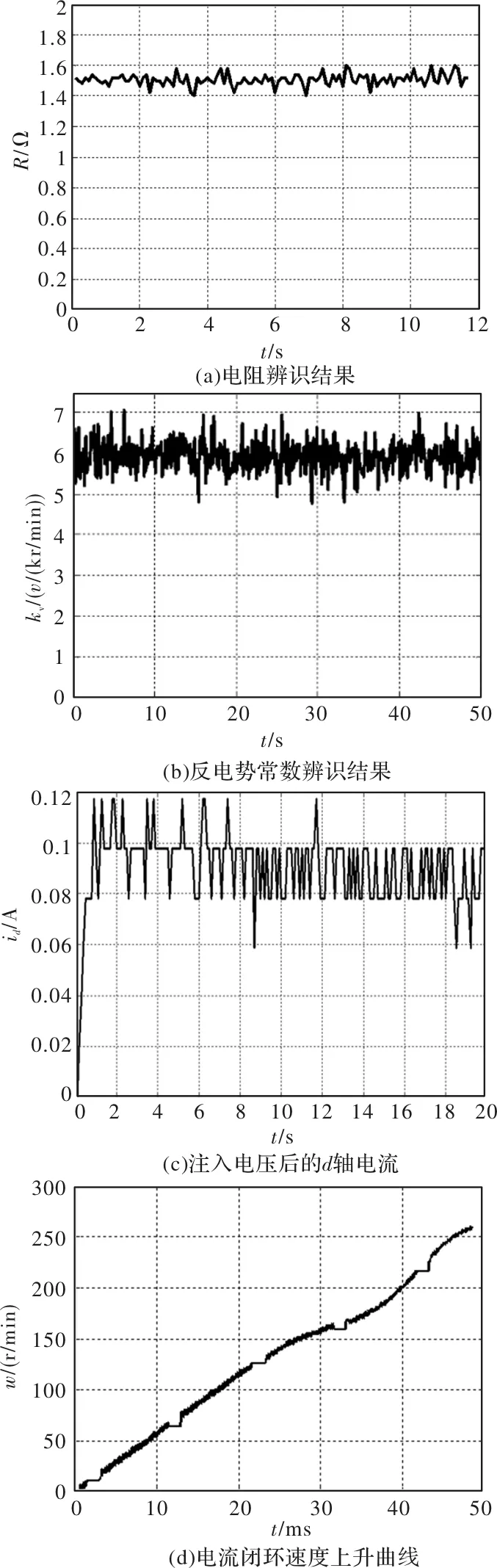
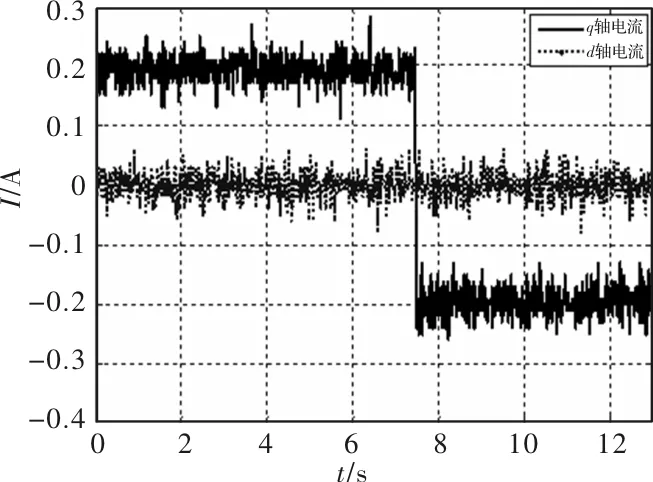
如公式所示，对于表贴式的同步电机而言，有Lq=Ld，可以只辨识一个电感参数即可。但对于内嵌式同步电机，由于Ld

控制uq=0，给定一个固定的ud，此时电机转子静止不动，ω=0，则

(23)

(24)

此外，这里需要注意的是，ud、uq是由三相定子相电压转化而来，与直流母线电压之间存在一个的比例关系，具体可通过式(25)计算：

(25)

则有：

(26)

3.3 转矩常数及反电势系数辨识

根据同步电机电压方程，采用id=0的控制方法，同时根据前面辨识的参数将电机控制器调整为电流闭环，则当电机运行到稳态时，有如下关系:

(27)

则此时可知反电势系数如下：

(28)

根据前面的分析可知，转矩常数可由下式求得：

kt=0.01654·kv

(29)

3.4 转动惯量辨识

根据同步电机的转矩方程

(30)

根据前面的分析，相比电机转子转动惯量，同步电机阻尼系数通常很小，甚至可忽略不计，为此，可以采取以下的近似方法获取电机转动惯量

(31)

需要注意的是，在该部分实验过程中，将控制器置为电流闭环。

4 实验验证

为验证所提出方法的有效性，搭建了永磁同步电机伺服驱动平台，将所提出的方法进行了实验验证。实验所用的伺服电机为科尔摩根公司研制的AKM21G系列伺服电机，电机上带有旋转变压器作为位置传感器，电机主要参数及辨识结果如表1所示。

表1 电机主要参数

从表1中可以看到对于同步电机电流环和速度环所需要的模型参数，均可辨识出来。从辨识精度来看，除电感参数误差略大于10%，其余参数误差都控制在10%以内。由于两个环路通常都是采用PI控制器，其对模型参数都有较宽的适用范围，因此，所辨识的参数误差在可接受范围内。图3(a)和图3(b)展示了电阻、反电势常数的辨识结果。图3(c)展示了电感辨识时，d轴注入电压后，其电流随时间上升变化的结果。图3(d)展示的是采用辨识出的电阻及电感，设计出相应的电流环控制器后，电流闭环，速度开环时，给定电流下的速度上升曲线。

图3 同步电机参数辨识结果

利用所提出的方法辨识出的电阻和电感，给定电流环频率为250Hz，依据式(24)设计相应的控制器后，其电流闭环结果如图4所示。给定电流分别为0.2A和-0.2A。可以看到d轴电流一直稳定在0附近，q轴电流能迅速响应到所给定的参考电流。

图4 电流环闭环结果

5 结 论

本文从永磁同步电机数学模型入手，分析了永磁同步电机电流环、速度环控制器设计所依据的4个模型参数。并基于此，对控制器设计所需的4个模型参数进行辨识，所提出的辨识方法均具有较强的可操作性。为验证所分析的控制器设计方法以及参数辨识方法，搭建了相应的永磁同步电机伺服驱动平台，针对所选用的AKM伺服电机，对其主要的模型参数进行辨识及控制器设计。实验结果证实了理论分析的正确性以及参数辨识及控制器参数设计的可行性，从而实现了控制器参数的自整定，实验数据也表明所提出的方法具有较好的工程使用价值。