影响风力发电机翼型气动性能的因素研究*

吴友健 杨 艺,2

（1.广东海洋大学 机械与动力工程学院；2.南方海洋科学与工程广东省实验室）

0 引言

化石能源的过度消耗使得全球气候变暖问题越来越严重，世界各国都在寻找清洁的可再生能源来实现可持续发展。风能作为一种环保能源受到大家的重视[1-2]，风力发电成为一种新兴的发电技术，许多国家都积极开展风力发电机的研究工作[3]。风力机有垂直轴和水平轴两种[4]，其中升力型垂直轴风力机由于具有无需偏航机构可适应全向风、造价低、结构简单[5-6]等优点而被受到重视。其工作原理是当来流过升力型叶片时会产生升力，升力沿圆周运动的切线方向分力形成的力矩推动风轮转动从而带动发电机工作。叶片是风力发电机的重要组成部分，叶片翼型气动性能的优劣对风力发电机的发电效率有很大的影响，因此对影响翼型气动特性的因素进行深入研究是十分必要的。

国内外学者对此做了相关研究。吕黎等人采用XFLR5程序来探究NACA4409和NACA0015翼型的气动性能差异，结果发现对称翼型NACA0015在正负攻角范围内都具有稳定的气动性能[7]。王旱祥等人发现减小翼型的弯度有利于提升其气动性能[8]。贾双林等人对 NACA63A010、NACA0018、NACA23012、NACA4412翼型进行气动性能分析，结果发现在这四种翼型当中，对称翼型NACA0018的气动性能最好，最适用于垂直轴风力机[9]。LI Xingxing等人通过增加翼型厚度的方法来获得一种新翼型，并证明了该新翼型的气动特性优于原翼型[10]。

目前对于影响风力机叶片翼型气动性能研究主要针对某单一因素开展，本文拟采用数值计算方法对多个因素进行详细研究，可以为进一步深入研究翼型气动特性和翼型设计优化提供系统性参考。

1 翼型气动性能参数

图1为气流绕流翼型示意图。翼型受到的合力可分解为升力和阻力，升力方向垂直于流速方向，阻力方向平行于流速方向，来流流过翼型表面时，上翼面速度大，下翼面速度小，根据伯努利定理，流速大则压强小，流速小则压强大，上下翼面存在的压差即为翼型的升力。来流方向与弦线的夹角α记为攻角，不同攻角下翼型的气动特性有较大的差异。翼型的升力系数Cl和阻力系数Cd是表征翼型气动特性的重要无量纲参数，表达式为：

式中，v为来流风速，m/s；c为翼型弦长，m。

升阻比Cl/Cd是指升力系数与阻力系数的比值，升阻比是衡量翼型综合性能的重要参数，升阻比越高说明翼型的气动性能越好，风力机发电效率越高[11]。

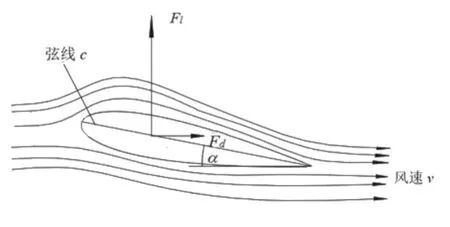
图1 翼型绕流示意图Fig.1 Airfoil flow diagram

2 翼型几何参数

翼型的气动特性主要取决于其几何形状，通常使用翼型的几何参数来表征其几何形状[12]。翼型的几何参数主要包括弦线、厚度、最大厚度、弯度及最大弯度，图2为翼型几何参数示意图。

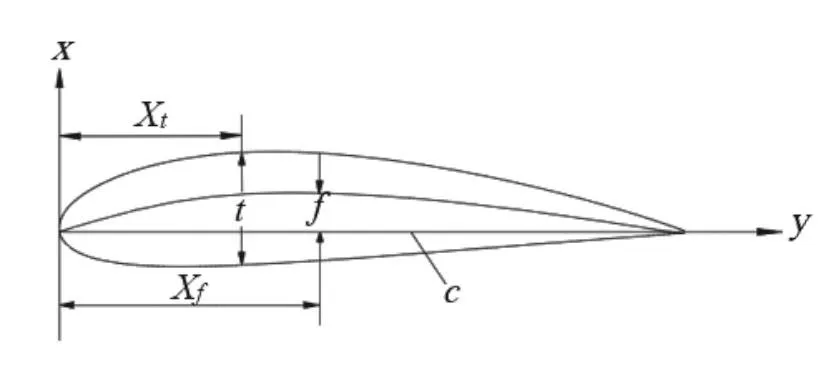
图2 翼型几何参数示意图Fig.2 Airfoil geometry parameter diagram

1）弦线c：翼型前缘至后缘的距离，其长度通常称为弦长。

2）最大厚度t：翼型上翼面与下翼面的最大距离。

3）最大厚度位置Xt：最大厚度所处位置与前缘的距离。

4）最大弯度f：翼型中弧线与弦线的最大距离。

5）最大弯度位置Xf:最大弯度所处位置与前缘的距离。

NACA翼型是美国宇航局开发的系列翼型，通常使用记号NACAXYZZ来表示，其中X表示翼型的最大弯度占弦长的百分比，Y表示翼型的最大弯度位置与前缘的距离占弦长的百分比；ZZ表示翼型的最大厚度占弦长的百分比[13]。以NACA2415为例，2代表翼型的最大相对弯度为弦长的2%，4代表翼型最大弯度位置与前缘距离为弦长的4%，15代表翼型的最大厚度为弦长的15%。通常我们将翼型的厚度与弦长的比值（t/c）称为相对厚度，弯度与弦长的比值（f/c）称为相对弯度。

3 数值模型

3.1 流场数值模型

风力机在低速下流动属于定常流动，空气可视为不可压缩气体，由于不考虑热量的传递故忽略能量方程，连续性方程和二维不可压缩N-S方程为[14]：

连续性方程：

N-S方程：

S-A（Spalart-Allmaras）是一个适用于低雷诺数流动单方程模型，通常被用于求解受到压力梯度作用的流动问题[15]，其输运方程为[16]：

3.2 数值求解

利用ICEM建立几何模型和进行结构化网格划分，网格数量为41 406。由于翼型近壁面处流场的参数变化梯度变化比较大，故在进行网格划分时对翼型近壁面处网格进行加密[17]。如图3所示，左侧为翼型整体网格分布图，右侧为翼型近壁面区域网格分布图。进口设置为速度进口，出口为压力出口，翼型壁面为无滑移壁面边界。建立基于S-A模型的数值计算，离散格式为二阶迎风格式，压力和速度耦合采用SIMPLE算法。当所有残差的最大值均小于10-5时，可以认为计算收敛。

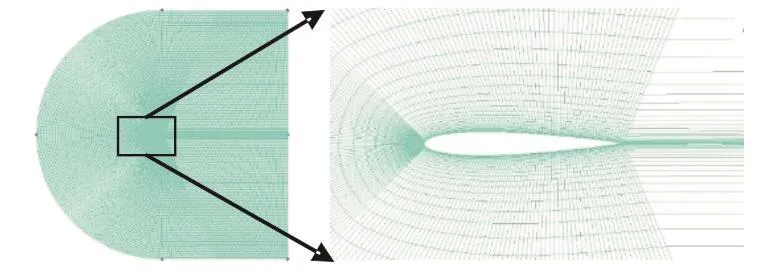
图3 翼型整体网格分布Fig.3 Airfoil overall mesh distribution

4 结果分析与讨论

4.1 数值方法验证

采用本文数值模拟方法模拟风洞测试的NACA0012翼型[18]气动性能，并将其结果与风洞试验值进行对比，验证数值方法的正确性。文献报导的风洞试验，研究雷诺数 Re=106，攻角范围为-18°-18°时NACA0012翼型的升力系数和阻力系数。选取其中部分攻角下的气动性能参数进行验证。图4和图5为翼型升力系数、阻力系数随攻角变化曲线，结果表明数值方法得到的升力系数与实验值趋势相同且误差很小，阻力系数有一定的差异，但误差在允许范围内，说明数值模拟方法可以准确有效模拟翼型气动性能。

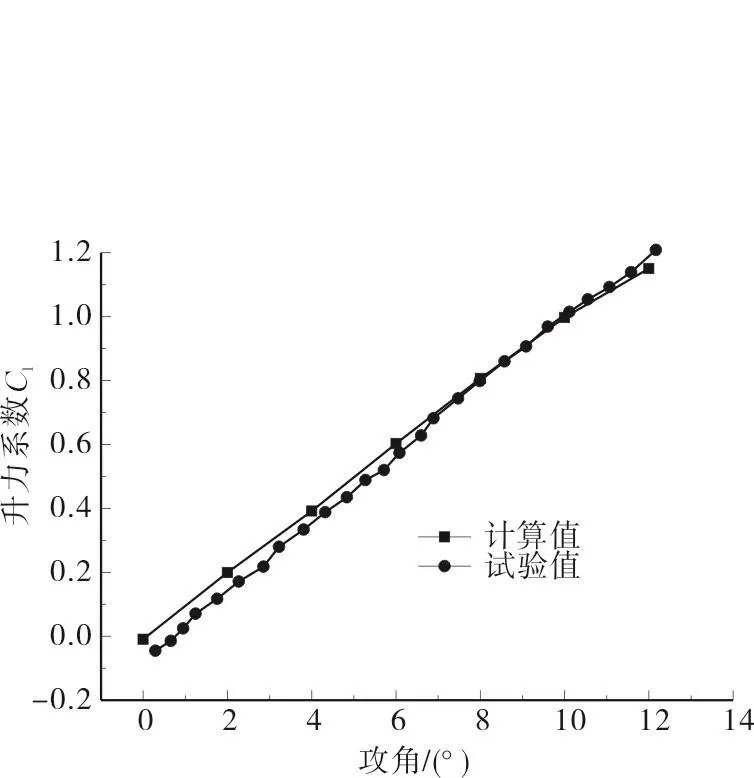
图4 NACA0012升力系数随攻角变化Fig.4 NACA0012 lift coefficient changes with angle of attack

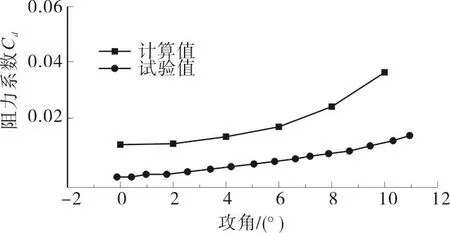
图5 NACA0012阻力系数随攻角变化Fig.5 NACA0012 drag coefficient changes with angle of attack

4.2 影响翼型气动特性的因素

翼型的气动特性随着攻角的变化而改变，故攻角是影响其气动特性的关键因素。除此之外，翼型的相对厚度、相对弯度及雷诺数都是影响翼型气动特性的因素。

4.2.1 相对厚度（t/c）对翼型气动特性的影响

选取NACA中的三种对称翼型进行研究，分别为NACA0014、NACA0016、NACA0018，其中，00代表翼型的相对弯度为零，即中弧线与弦线重合；翼型的最大厚度分别为弦长的14%，16%，18%，图6为三种翼型的几何轮廓示意图。

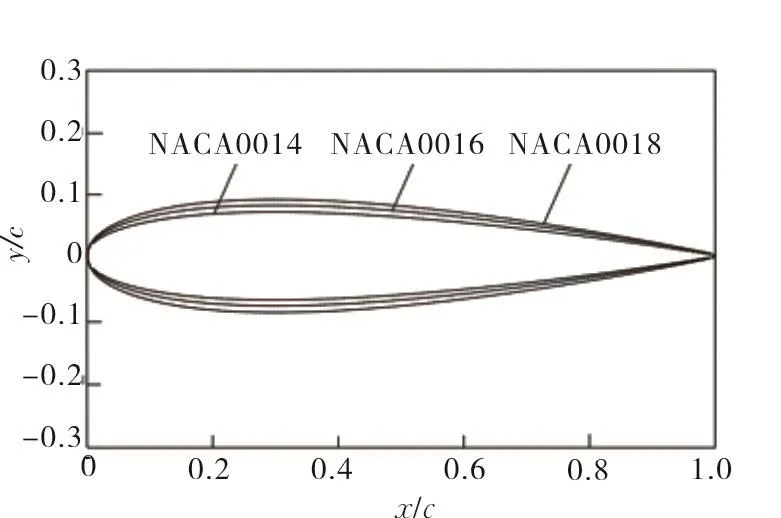
图6 不同相对厚度翼型几何轮廓对比Fig.6 Comparison of geometric profiles of different relative thickness airfoils

由图7可得，当攻角小于12°时，三种翼型的升力系数随着相对厚度的增加而减小，在12°攻角时三种翼型的升力系数达到最大值；随着攻角的继续增大，升力系数开始下降，在16°攻角时达到最小值0.65。由图8可得，在0°-12°攻角范围内三种翼型的阻力系数差异不大，阻力系数曲线接近重合。当攻角大于12°时，阻力系数开始快速上升，且翼型的相对厚度越小阻力系数越大。当攻角超过某一临界角后，翼型的升力系数下降、阻力系数上升的现象称为失速，此时三种翼型失速临界攻角近似为12°。

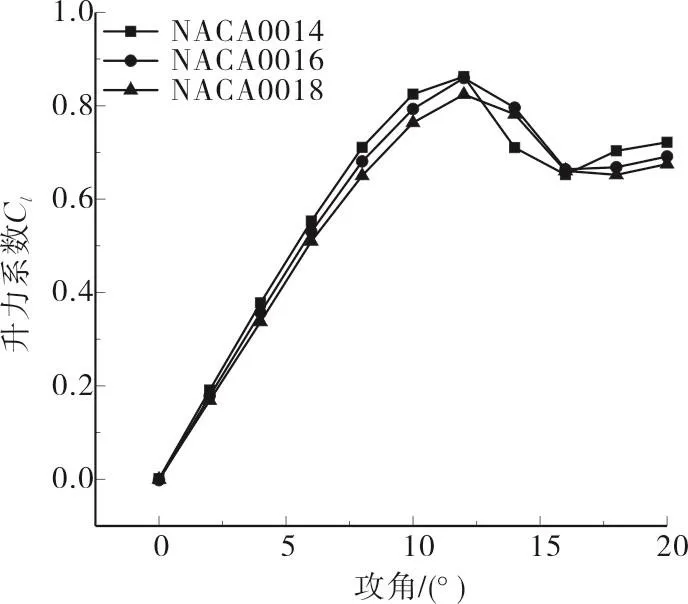
图7 不同相对厚度翼型升力系数随攻角变化曲线Fig.7 Different relative thickness airfoil lift coefficient changes with angle of attack

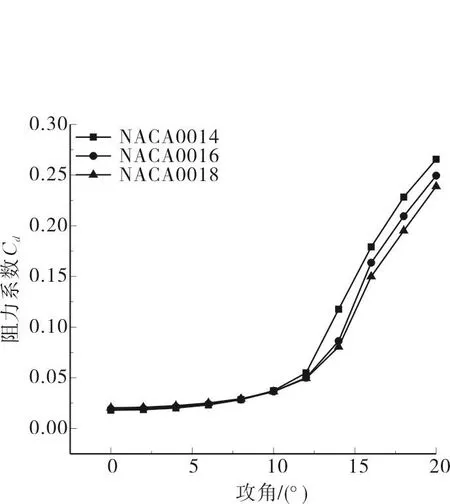
图8 不同相对厚度翼型阻力系数随攻角变化曲线Fig.8 Different relative thickness airfoil drag coefficient changes with angle of attack

由图9可得，在0°～20°攻角范围内，升阻比呈现出先增大后减小的变化趋势。三种翼型的最大升阻比均在8°攻角时出现，且相对厚度越小，最大升阻比越大。随着攻角的继续增加，翼型的升阻比开始下降，相对厚度对翼型升阻比的影响逐渐减小。

图9 不同相对厚度翼型升阻比随攻角变化曲线Fig.9 Different relative thickness airfoil lift-to-drag ratio changes with angle of attack

图10和图11分别为三种翼型在6°和16°攻角时的流线图。由图可知，在6°攻角时，翼型没有出现旋涡，而在16°攻角时，翼型已经出现较大的分离涡，气流分离现象十分严重，翼型进入严重的失速状态。在16°攻角时，三种翼型都出现较大的旋涡，其中NACA0014的分离点与前缘距离0.15c（c为弦长），NACA0016的分离点与前缘距离0.20c，NACA0018的分离点与前缘距离0.28c。由此可得，当翼型处于失速状态时，相对厚度越小，涡的范围越大，与前缘的距离越近，翼型的失速越严重。当攻角超过失速角后，翼型的边界层会发生分离，其尾部形成旋涡，导致压差阻力大大增加，翼型的气动性能急剧下降进入失速状态。这也解释了图7和图8中当攻角超过12°后，为何翼型的升力系数下降、阻力系数显著上升。

综上所述，在攻角小于失速攻角时，相对厚度小的翼型可以获得更好的气动性能效果；当攻角大于失速角后，相对厚度大的翼型的气动性能更佳。

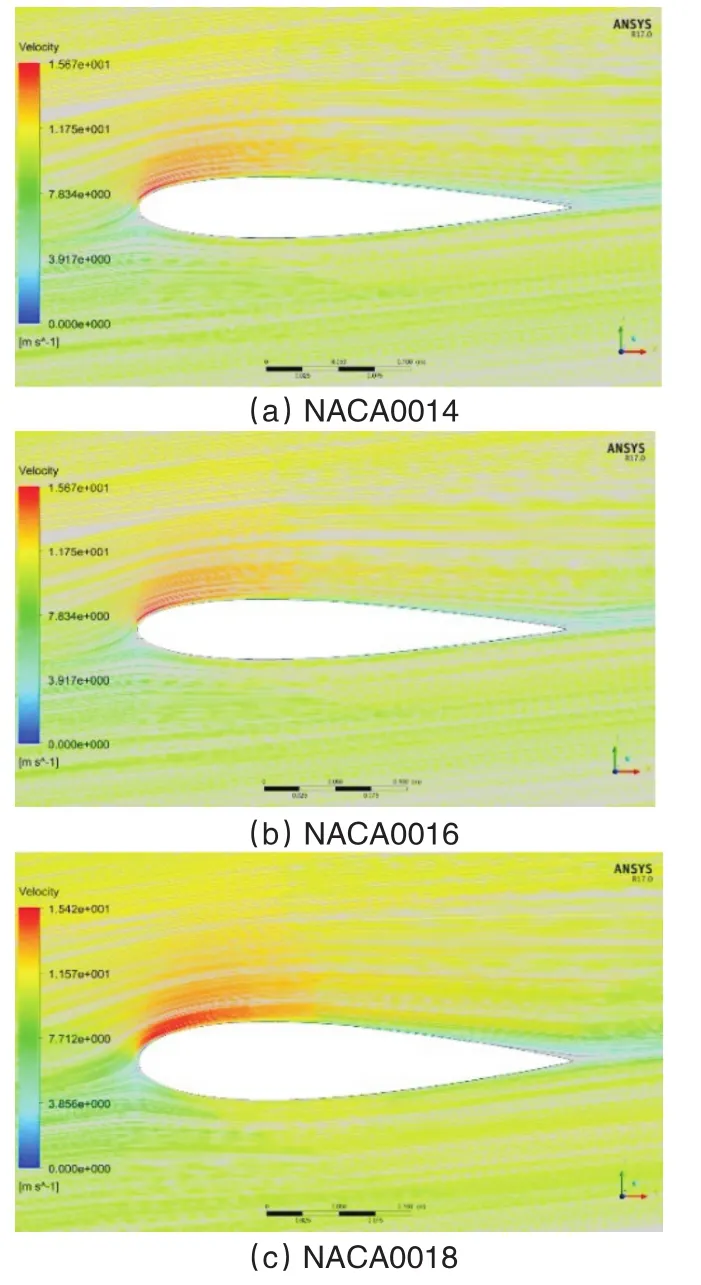
图10 6°攻角时翼型速度流线图Fig.10 Airfoil speed streamline diagram at 6°angle of attack

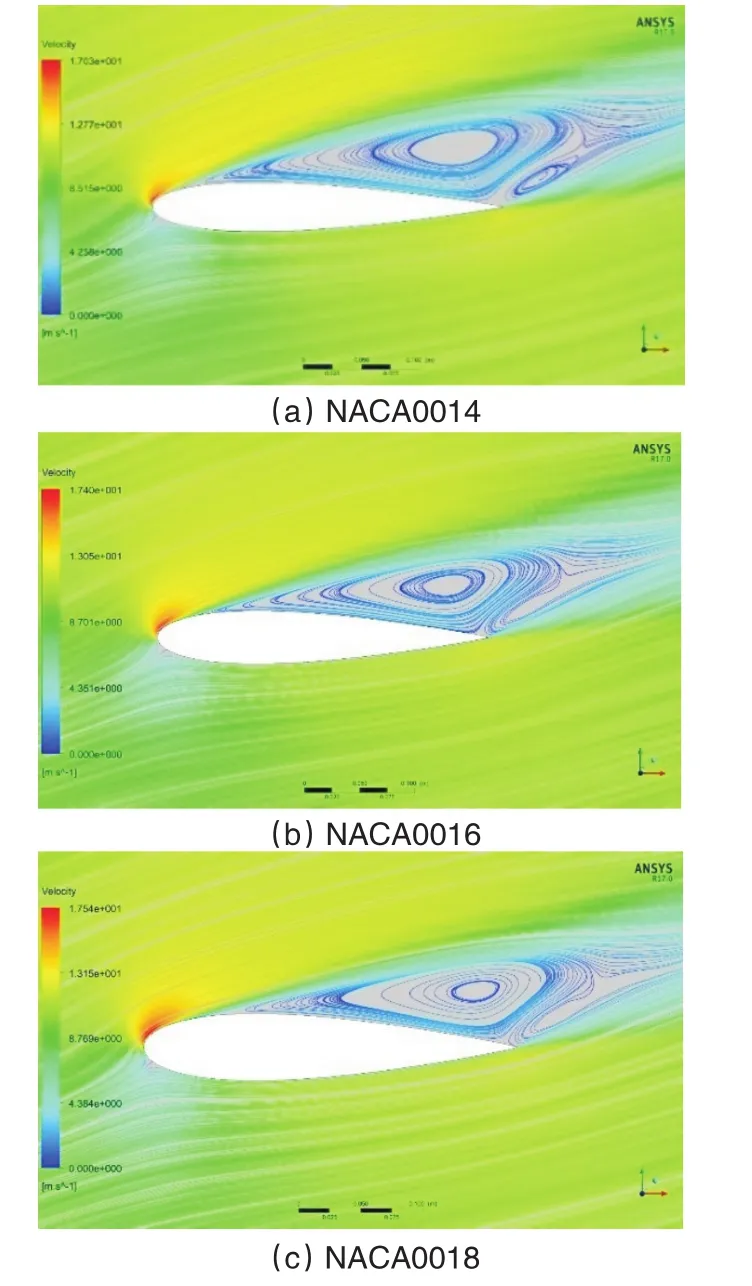
图11 16°攻角时翼型速度流线图Fig.11 Airfoil speed streamline diagram at 16°angle of attack

4.2.2 相对弯度（f/c）对翼型气动特性的影响

选取NACA0018、NACA2418、NACA4418三种翼型来分析相对弯度对翼型气动特性的影响，三种翼型最大弯度占弦长的百分比分别为0%、2%、4%，图12为三种翼型的几何轮廓示意图。

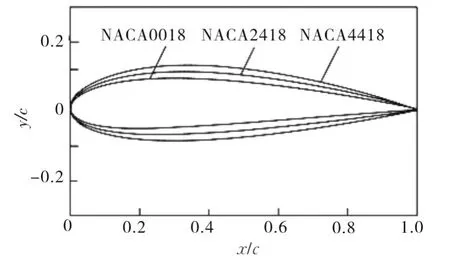
图12 不同相对弯度翼型几何轮廓对比Fig.12 Comparison of geometric profiles of different relative camber airfoils

由图13可知，在0°～20°攻角范围内，翼型的升力系数随着相对弯度的增加而增大。在12°攻角时，三种翼型的升力系数均达到最大值，随后升力系数开始下降。由图14可知，在0°～12°攻角范围内，三种翼型的阻力系数差异较小；当攻角大于12°时，三种翼型的阻力系数开始快速上升，但差异仍然不大。

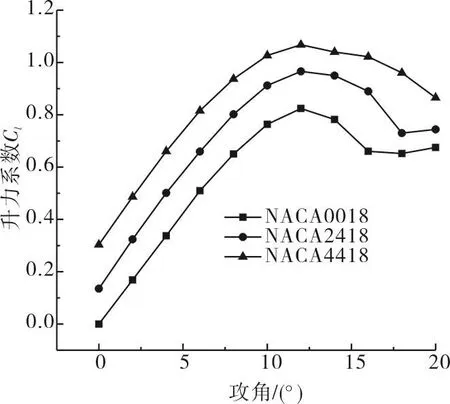
图13 不同相对弯度翼型升力系数随攻角变化Fig.13 Different relative camber airfoil lift coefficient changes with angle of attack

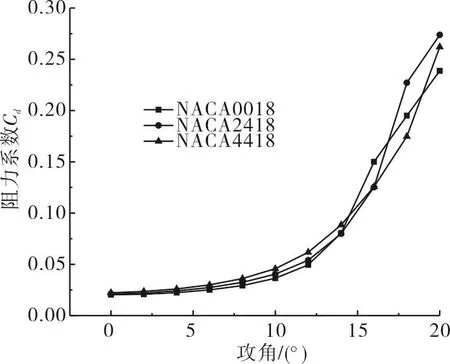
图14 不同相对弯度翼型阻力系数随攻角变化Fig.14 Different relative camber airfoil drag coefficient changes with angle of attack

由图15可知，翼型的升阻比呈现出先增大后减小的趋势，且翼型的相对弯度越大，不同翼型的最大升阻比越大，其最大升阻比所对应的攻角越小。当攻角超过失速角后，翼型升阻比受相对弯度的影响开始逐渐减小。

图15 不同相对弯度翼型升阻比随攻角变化Fig.15 Different relative camber airfoil lift-to-drag ratio changes with angle of attack

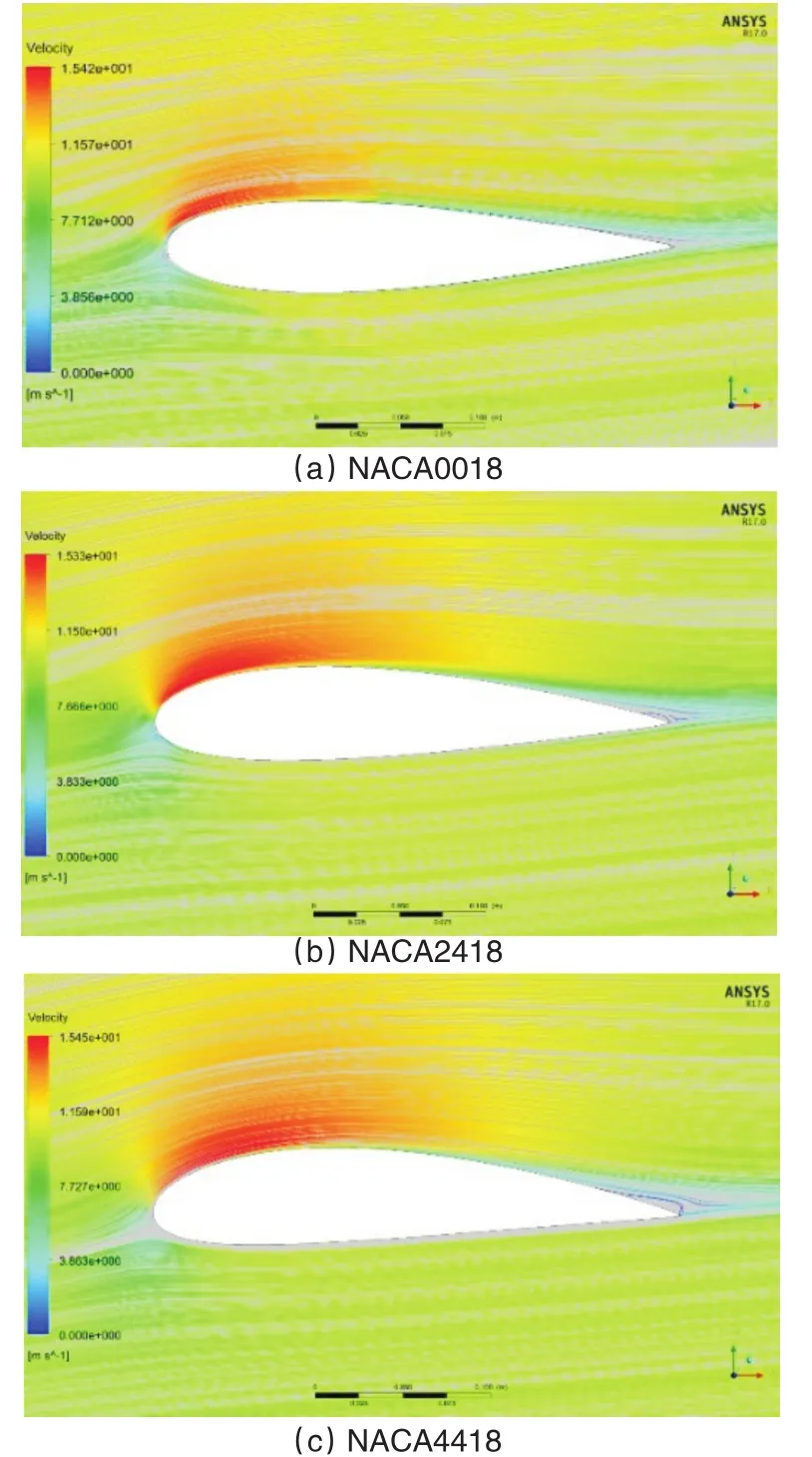
图16 6°攻角时翼型速度流线图Fig.16 Airfoil speed streamline diagram at 6°angle of attack

图17 16°攻角时翼型速度流线图Fig.17 Airfoil speed streamline diagram at 16°angle of attack

图16和图17分别为翼型在6°和16°攻角时的速度流线图，在6°攻角时相对弯度越大，流动分离出现得越早，涡的形成也越早。在16°攻角时，三种翼型都出现严重的气流分离，其中NACA0018的分离点与前缘距离0.26c（c为弦长），NACA2418的分离点与前缘距离0.36c，NACA4418的分离点与前缘距离0.48c。由此可得，当翼型未失速时翼型的弯度越大其尾部涡的出现越早；当翼型处于失速状态时，弯度越小涡的范围越大，与前缘的距离越近，翼型的失速越为严重。

综上所述，在0°～20°攻角范围内，相对弯度越大翼型的气动性能越佳。

4.2.3 雷诺数对翼型气动特性的影响

雷诺数是一个可以用于判断流体流态的无量纲参数，其实质是指流体的惯性力与粘性力的比值，通常用Re表示。雷诺数对叶片翼型的气动特性有较大的影响[19]，因此研究不同雷诺数下翼型的气动参数十分有必要，图18～图20为翼型在不同雷诺数下的NACA0018翼型气动特性参数随攻角变化曲线。

由图18可得，当攻角小于5°时，不同雷诺数下的升力系数没有太大的差异，曲线几乎接近重合。随着攻角的继续增大，升力系数曲线开始分离，且雷诺数越大升力系数越大。由图19可知，翼型的阻力系数随着雷诺数的增加而减小，并且翼型所对应的失速攻角越大。从整体上看，翼型的升阻比随着雷诺数增加而增大，且最大升阻比所对应攻角越大。当攻角超过失速角后，雷诺数对升阻比的影响开始逐渐减小，升阻比曲线有重合的趋势。

图18 不同雷诺数时NACA0018翼型升力系数随攻角变化Fig.18 NACA0018 airfoil lift coefficient changes with angle of attack with different Reynolds numbers

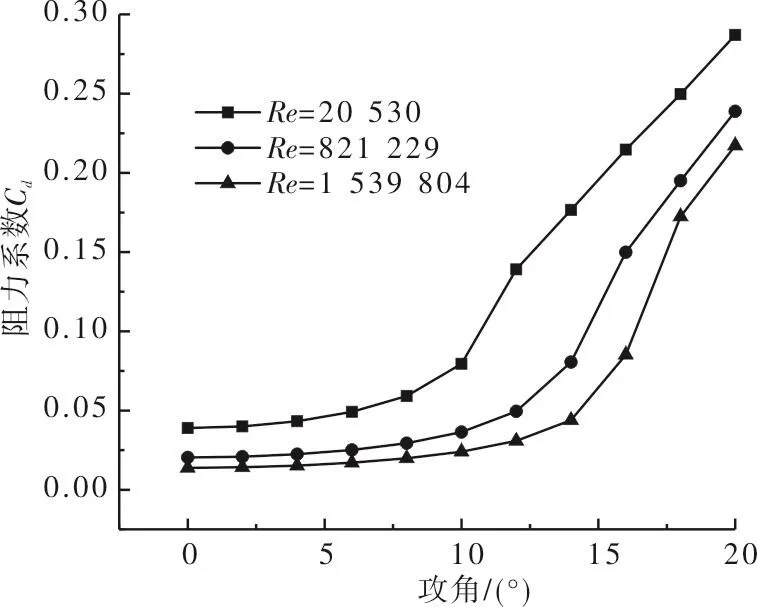
图19 不同雷诺数时NACA0018翼型阻力系数随攻角变化Fig.19 NACA0018 airfoil drag coefficient changes with angle of attack with different Reynolds numbers

图20 不同雷诺数时NACA0018翼型升阻比随攻角变化Fig.20 NACA0018 airfoil lift-to-drag ratio changes with angle of attack with different Reynolds numbers

5 结论

本文系统研究影响翼型气动性能的因素，主要得到如下结论：

1）基于FLUENT软件建立S-A模型对攻角范围为-18°-18°时NACA0012进行数值计算，并与文献风洞试验得到的升力系数和阻力系数数据进行比较，结果表明计算值与试验值吻合，验证了数值方法的正确性。

2）当攻角小于失速角12°时，翼型的升阻比随着相对厚度的增大而减小；随着相对弯度的增大而增大。当翼型处于失速状态时，翼型的相对厚度和相对弯度越小，其尾部出现的涡越大，与前缘的距离越近，流动分离的速度越快。

3）比较不同雷诺数NACA0018翼型的气动特性参数，结果表明雷诺数越大，翼型的升力系数、升阻比越大，翼型的气动性能越好。