基于COMSOL的非牛顿流体在管道中的流动特性研究＊

李亚飞，周 懿，胡 钺，高 政

（船舶动力工程技术交通行业重点实验室，湖北 武汉430063；武汉理工大学 能源与动力工程学院，湖北 武汉430063）

1687年牛顿提出，作一维剪切流动的水，其剪切应变速率与剪切应力的大小成正比，这个规律就是后来著名的牛顿内摩擦定律。在流变学中，流变性符合这一规律的流体被称作牛顿流体；反之，则为非牛顿流体。相比于牛顿流体，非牛顿流体在工农业生产乃至医学研究中出现得更为广泛，比如石油钻井采出液的集输处理、聚合物塑料制品加工、人体血液在血管中的流动等。上述这些情形都涉及非牛顿流体在管道内的流动问题，因此非牛顿流体在各种管道环境下的流动机理具有充分的研究价值。1867年，J.C.麦克斯韦提出线性黏弹性方程，开始了非牛顿流体力学的研究。但由于黏弹性流体问题具有的复杂性，一直到20世纪50年代后相关研究领域才得到较为迅速的发展，并逐渐成为一门独立的学科[1]。相比牛顿流体在管道流动领域已较为成熟的研究成果，关于非牛顿流体的研究还有很大的发展空间。针对非牛顿流体的研究方法主要包括实验法、解析解法与数值解法。实验法最为直接，可检验其他方法的正确性，但是成本较高且实验结果的普遍性不佳。解析解法是理论上最为准确理想的研究方法，通过建立合适的微分方程组，使用纯数学方法得出方程的精确解；但对于非牛顿流体复杂的流动情况来说，求解的难度过大。数值解法则是应用计算机将物理场离散化，之后将流体微分方程组转化为代数方程并求出各个节点上的参数值，属于一种近似解法[2]。由于数值解法容易获得且能保证足够的求解精度，其已经成为研究非牛顿流体问题最为常用的方法。

国外学者对非牛顿流体的研究开始最早。在圆管道方面，CHEBBI[3]使用积分边界层方法，分析了幂律流体层流在圆管入口段与充分发展区的流动特性，获得了与实验数据吻合度较高的结果。对于非圆管道，GUCKES[4]使用有限差分法求解幂律流体和宾汉流体，给出了2种流体在偏心圆环管中流动的平均体积流率。MITSUISHI等人[5]使用高聚合物非牛顿流体作为实验材料，给出了偏心圆环管中非牛顿流体流速与压降之间的关系。

国内对于非牛顿流体管内流动的研究起步较晚，成果也较国外少。姜笃志[6]分析了非牛顿流体在管道内流变性的一般规律并建立模型。杨旭等人[7]分析了非牛顿流体的本构及流动规律，基于空间分数阶微积分方法，建立了分数阶非牛顿流体本构模型，使用分数阶的阶数大小来反映非牛顿流体流动的空间记忆性强弱。

经过以上分析可以看出，中国对非牛顿流体管内流动这一研究领域的研究不太成熟，大多数停留在对非牛顿流体管内流动进行基本的数值模拟这一阶段，而缺少对于模拟条件的多样化拓展以及对结果数据之间关系更加详尽的讨论。关于非牛顿纳米流体管内流动这一新兴领域更是空白。又考虑到非牛顿流体管内流动在工业上的广泛应用，进一步进行相关方面的数值研究是很有必要的。

本文使用COM SOL Multiphysics这一软件作为计算平台，采用有限元分析法对非牛顿流体流经不同管道时体现出的流动特性进行数值模拟研究。

1 数学模型与数值模拟方法

1.1 控制方程组

一切的流体流动过程，都以以下3个基本的物理学原理为基础：质量守恒定律，牛顿第二定律与能量守恒定律。将这些物理学用于构建流动模型，将会导出一组方程，即连续性方程、动量方程与能量方程。这些方程是上述物理学原理的数学描述，本文不讨论传热，所以不引入能量守恒方程，质量守恒定律（连续性方程）：

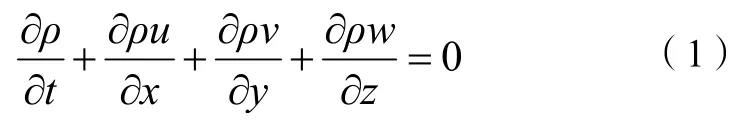
式（1）表示的是瞬态三维可压流体流动的连续性方程，本文所分析的流体流动处于稳态且不可压缩，密度ρ不会随着时间的变化而改变，所以，流体流动的数学描述为：

式（3）（4）（5）是对于任何流体都成立的动量守恒方程，是微元体内流体动量对于事件的变化率等于外界作用于该微元体上的各种力的和。简称动量方程，也称纳维斯托克斯（N-S）方程。

1.2 本构方程

本构方程是反映物料宏观性质的数学模型，又被称为流变状态方程或是流变方程。在流变学中，本构方程是在某些假定条件下，对流体或弹性体的材料力学行为的数学描述，可以用来区分流体类型。前述的牛顿内摩擦定律即最简单的流体本构方程。本构方程与连续性方程、运动方程一起构成封闭的方程组，用于求解流体的流动特性。

在本文仿真中使用的幂律流体的本构方程式为：

式（6）中：m为黏稠系数，Pa·sn，表示物料的黏稠程度；n为幂律流变指数（简称幂律指数），为无量纲量，表示非牛顿流体的流动特性偏离牛顿流体的程度（n=1时为牛顿流体）。

1.3 非牛顿流体管道流动模型

1.3.1 流体切应力

对于圆形管道内的流体流动，非管壁处流体剪应力ô与管壁处剪应力ôw的取值满足下列均匀流动方程式：

式（7）（8）中：Δp为管道压降；r为圆柱坐标系中的r方向坐标位置；L为管道长度；R为管道半径。

1.3.2 剪切应变速率

剪切应变速率描述的是流体的剪切流动，定义为单位时间的剪切应变变化：此选用的是COMSOL Multiphysics中的Laminar flow求解器模块。这个模块内置了许多流动的基本物理参数，可以在这些参数的基础上结合前文所述的数学模型定义更多仿真所需要的变量。

式（9）中：γ为剪切应变。

值得注意的是，剪切应变速率常与速度梯度混淆。实际上二者是不同的概念。速度梯度是流体的速度对空间坐标的导数，用du/dy来表示。在数学上，二者的数值有时相等，这是因为一般速度梯度符合：

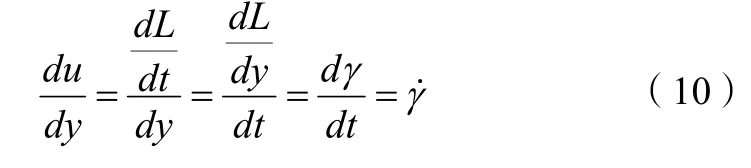
但二者的物理意义并不相同，且数值上有时并不相等（如流体在同轴圆筒之间的流动，此时有角速度的影响）。

1.3.3 广义雷诺数

对于圆管内非牛顿流体流动的雷诺数Re计算，目前多是仿照牛顿流体，近似按照黏度或者对比牛顿流体压降的公式计算其广义雷诺数Re´：

式（11）中：D为圆管直径；n为流变指数，不同流体二者的取值不同；k为流变系数。

对于牛顿流体来说，n´=1，k´=μ。所以，牛顿流体雷诺数为：

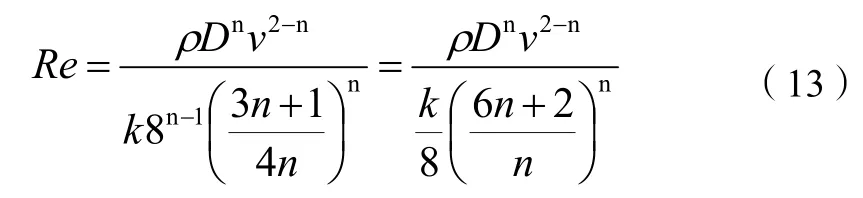
1.4 求解器介绍

本次模拟使用的COM SOL Multiphysics是一款功能强大的多物理场仿真软件，可以对多个领域的物理过程进行模拟计算。本文研究的是非牛顿流体在管道内的流动特性，因上述均匀流动方程式的推导并没有涉及流体的性质与流动状态，所以该方程式适用于所有的流体与流动状态。

1.5 数值计算方法

本文涉及的数值计算使用的是有限元分析法（Finite elementmethod，FEM）。它的基本思路为：一个物体或系统被分解为由多个相互联结的、简单、独立的点组成的几何模型。在这种方法中这些独立的点的数量是有限的，因此被称为有限元。由实际的物理模型中推导出来的平衡方程式被使用到每个点上，由此产生了一个方程组，这个方程组可以用线性代数的方法求解。

1.6 网格局部加密与独立性验证

在数值仿真过程中，网格的数量与大小与仿真结果的精度密切相关。更多的网格数目虽然能够提高结果的精度，但是也意味着要耗费更多的计算机算力资源。经衡量，使用COMSOLMultiphysics中的Meshrefine功能对模型的关键计算区域进行局部网格加密，模型的其他部分则保持相对较大的网格密度。

局部加密效果如图1所示。

图1 网格局部加密效果图

此外，为了保证求解结果的精度，每组仿真计算时都需要多次调整网格的数量，检查计算结果是否因为网格密度不同而出现较大的误差。经过调整，确认每组仿真的网格数量保持在200万～400万之间为宜，这时求解精度已经足够。

2 仿真结果及分析

2.1 物理模型

2.1.1 几何模型

本组仿真选用了2种不同截面的长直管道，分别为圆形截面、矩形截面管道。这2种截面管道的形状示意与几何尺寸数据如图2和表1所示，管道整体如图3所示。

图2 管道截面形状与尺寸示意图

表1 管道几何尺寸数据

图3 管道整体示意图

非牛顿流体从管道的一端流入，在管道内进行流动过程后，从另一端流出。

此后的时间里，王施凯仿佛突然被打通了任督二脉，开始发愤图强，努力学习……过了一个春·天一个夏天后，期末考试他竟真的考到了班级中游。王施凯本人的说法是有天晚上起夜，发现老爸在看他小时候的照片和奖状，一时间激发了奋斗的意志。当然，大老爷们半夜抹眼泪这种事情他是不会告诉赵明月的。赵明月也没多问，心照不宣地继续为他讲题。

2.1.2 流体性质

本组仿真选用的非牛顿流体为幂律流体（幂律指数n≠1），其黏度与剪切应变速率的关系遵循下式：

其余的流动特性参数列如表2所示。

表2 不同截面管仿真中非牛顿流体的流动特性参数值

2.2 边界条件

选用如下边界条件：①进口边界条件。进口速度uin，取值固定为0.15m/s；进口温度Tin为293.15K（20℃）。②出口边界条件。出口压力为0。③壁面边界条件。无滑移边界条件，即壁面处的流体速度为0；常壁温边界，壁面温度TW为333.15K（60℃）。④其他。流体不可压缩，所有管道区域内流体处于层流状态。

2.3 幂律指数对非牛顿流体管道流动的影响

对于幂律流体，当幂律指数n＜1时，流体表现出剪切稀化效应；当幂律指数n＞1时，流体表现出剪切增稠效应。为了探究幂律指数n对幂律流体在管道中流动特性的影响，控制进口速度uin=0.15m/s，管截面当量直径de=0.1m，管长l=0.8m，参数相同，幂律流体n取0.6～1.4，对圆形截面管道内的非牛顿幂律流体进行流动特性的仿真。不同幂律指数下非牛顿幂律流体的速度场分布如图4所示。

图4展示了不同幂律指数条件下幂律流体在管道各个横截面上的速度场分布。观察靠近管道入口段的速度场横截面，可以发现随着n的增大，流体的速度入口段长度越来越短。这是因为当幂律指数n＞1时，流体表现出剪切增稠效应，而且该效应会随着n的增大而得到强化（剪切稀化效应同理）。剪切增稠效应下的流体流动性降低，速度梯度小，更容易达到充分发展状态；反之，剪切稀化效应下的流体流动性提高，速度梯度大，速度入口段长。

此外，幂律指数也对流体充分发展区最大速度有一定影响，两者呈正相关关系。上述结论均可以从MUKHERJEE的研究中得到验证。

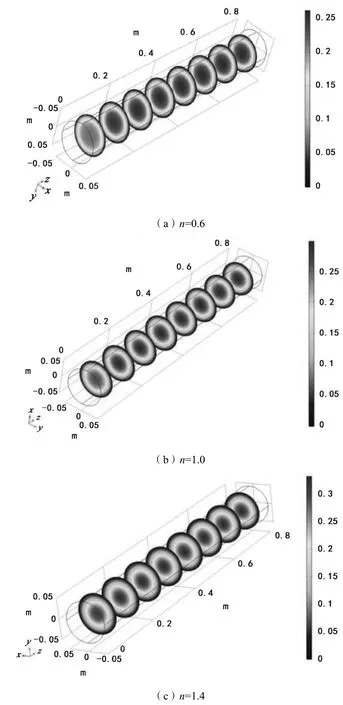
图4 不同幂律指数下非牛顿幂律流体的速度场分布（单位：m/s）

2.4 截面形状对非牛顿流体管道流动的影响

保持进口速度uin=0.15m/s，幂律指数n=0.6，管截面当量直径de=0.1m，管长l=0.8m，参数相同，对不同截面管道内的非牛顿流体进行流动特性仿真。

2.4.1 截面形状对速度入口段长度的影响

在本组仿真中，在各管道的轴向中心截面上绘制速度云图，观察非牛顿流体在不同截面管道中的速度入口段长度。不同截面形状管道轴向中心截面速度云图如图5所示，从图5可以看出，流体在管道入口段形成速度边界层，边界层逐渐向截面中心流动汇集，最后消失形成稳定的流态。矩形形状的管道内非牛顿流体的速度入口段长度比圆形管道的长。这说明速度入口段的长度与管道截面形状有关。截面为圆形的管道内的非牛顿流体更早到达充分发展阶段，流态更为稳定。

图5 不同截面形状管道轴向中心截面速度云图（单位：m/s）

2.4.2 截面形状对速度场分布的影响

为了更直观地观察出管道内的速度场分布情况，重新选取数个沿管道轴向等距分布的管道横截面来绘制速度云图。通过观察每个截面云图的变化过程，可以得出非牛顿流体的速度沿径向与轴向发展的情况。两种截面形状管道的横截面速度场分布如图6所示，从图6可以看出，流体在管壁处速度为0，最大速度中心位于各管道的横截面几何中心区域，但并不是一开始就在中心区域达到最大速度。在2种管道靠近入口段的截面，可看到速度最大值区域分散在截面的几何中心周围。对于矩形截面管道来说这种现象更为明显，云图中能够看到入口段截面形成两三个速度中心区域，由此可见，速度最大区域首先出现在靠近管道截面角区的位置，之后在向轴向发展的同时向径向截面几何中心合并，最终在中间达到流动速度峰值。

3 结论

本文通过COMSOLMultiphysics平台，使用有限元法与局部优化网格技术建立了非牛顿流体在不同横截面管道中的流动模型。

图6 两种截面形状管道的横截面速度场分布（单位：m/s）

通过以上数值模型，分析了非牛顿流体在管道内的速度分布，并讨论了流体流动特性参数之间的关系，以及管道截面形状和幂律指数对流体流动性能的影响。具体总结如下：对于幂律流体，更高的幂律指数n值将使流体更多表现出剪切增稠效应，进一步使得速度入口段长度逐步减短；反之，则表现出剪切稀化效应，增长速度入口段的长度。在相同的边界条件下，横截面为矩形的管道中流体的速度入口段长度最长，随后为圆形截面管道；管道内流体流动的发展从接近截面角区的位置开始，之后再向管道截面几何中心处发展。