基于双频蝙蝠算法的树状灌溉管网规划

吕石磊，卢思华，魏志威，李震*，吴奔雷

基于双频蝙蝠算法的树状灌溉管网规划

吕石磊1,2，卢思华1，魏志威1，李震1,2*，吴奔雷1

(1.华南农业大学电子工程学院，广东 广州 510642；2.国家柑橘产业技术体系机械化研究室，广东 广州 510642)

以管网投资费用最低为目标，建立了改进的自压树状灌溉管网规划模型，通过定义管网用水节点的上层水节点来保证管道连通性；同时，提出了改进的双频蝙蝠算法，通过使用双脉冲频率策略均衡算法多样性与收敛性。基于12个100维度测试函数的寻优结果表明，与遗传算法、粒子群算法及蝙蝠算法相比，双频蝙蝠算法能够有效提高全局搜索能力；应用双频蝙蝠算法分别对10节点和34节点的管网进行规划设计，管网投资费用均值较蝙蝠算法可分别减少23.60%和31.03%。

自压树状灌溉管网；管网部署；双频蝙蝠算法

灌溉管网是农业节水工程的重要组成部分[1]。树状管网结构简单、节省管材，是灌溉管网的主要部署形式，规划设计以管网投资费用最低为目标，包括管网部署规划和管道管径优化[2]。其中，管网部署规划以用水节点之间的管道部署为决策变量，寻求满足管网管道连通性的解决方案[3]。

业界曾探索应用神经网络[5]、图论[6]等方法来解决管网部署规划问题，并使用遗传算法(GA)[7]、粒子群算法(PSO)[8]等及其改进算法对管径进行优化设计。马孝义等[9]提出了基于整数编码GA算法的两级管网设计方法；杨建军等[10]基于环路方法生成了初始管网部署方案，使用GA算法对管道管径进行设计。这些研究本质上是对树状灌溉管网依次进行管网部署规划设计和管道管径优化设计，但未考虑二者之间的协调关系。现阶段，业界将管网规划设计问题描述为以用水节点之间的管网部署和管径尺寸为决策变量的离散组合优化问题，并使用智能优化算法对管网进行综合设计。李海滨等[11]提出了管网部署与管道管径同步设计的管网规划模型。在此基础上，IBRAHIM等[12]使用PSO算法求解了该管网规划模型；邱金亮等[13]研究了灌溉作业制度对管网设计的影响；朱成立等[14]使用蚁群算法对管网部署和管径优化进行了综合设计；AFSHAR等[15]使用了启发策略来解决给水管网的规划设计问题。这些研究多使用智能优化算法对管网规划进行同步设计，但是使用的管网规划模型未考虑用水节点之间的连通性问题，需要工程人员结合设计经验，事先提供管网的初步连接图，降低了管网规划模型的通用性。

笔者以自压树状灌溉管网为研究对象，以管网投资费用最低为目标，综合考虑管道部署和管径优化问题，寻求满足管网特定约束条件和管道连通性的最小应用成本方案，提出基于上层水节点的树状管网规划模型，并且提出改进智能优化算法对规划模型进行求解，以此来得到高效实用的树状管网规划设计方法。

1　自压树状管网规划模型的设计

1.1　管网规划模型

自压树状灌溉管网由水源点、用水节点及与节点之间的连接管道组成。在已知用水节点位置的情况下，管网设计可被描述为以管道长度为边、求解满足目标条件的加权有向图问题。以管网投资费用最低为目标，依据文献[8–13]，建立管网规划模型。

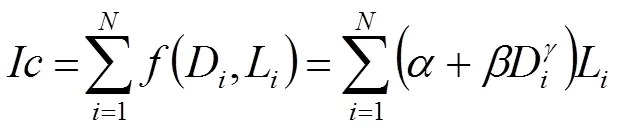
式中：为管网投资费用(元)；为用水节点之间的连接管道数量；D和L分别是管道的管径 (mm)和管长(m)；、和分别为管道造价系数和指数。

管网用水节点压力约束、管道流速约束和管径约束分别如式(2)、式(3)、式(4)所示。

min≤V≤max(3)

min≤D≤max(4)

式中：E为水源点的水面标高(m)；()为水源点与管道之间的连接管道数量(=1,2,…,)；为管网局部水头损失系数；、、表示与管材有关的管道水头损失系数；Q为管道流量(m3/h)；G为管道流入的用水节点地面高程(m)，P为该用水节点允许的最低水压(m)；max和min分别为管道允许的最大和最小流速(m/s)；max和min分别为管道可使用的最大和最小管径(mm)。

1.2　模型分析与改进

现有的解决方法均需要根据工程设计经验生成管网初步连接图[9–13]来保证管道连通性。通过引入上层水节点，笔者将最小管网投资费用问题转换为对用水节点及其对应不同上层水节点的选择组合问题，以此来保证管道连通性，无需管网初步连接图，以提高管网规划模型的扩展性。

1) 根据树状灌溉管网的单点供水原则[9]，若管网除水源点外存在个用水节点，则一定存在条连接管道，因此，为保证管网的管道连通性，对于任一用水节点N(=1,2,…,)，有且只有1条连接管道与之相连，并向其供水。

2) 记与管道另一端相连的节点为N(≠)，则节点N为节点N的上层水节点，即水流通过管道，由节点N流向N。若节点N为水源点，则根据管网的节点压力约束可知，自压树状灌溉管网水源点的水面标高E应大于节点N的地面高程G，如式(2)所示；若节点N不为水源点，从增加管网鲁棒性角度出发，令G≥G，则使得在水源点不作业或发生故障的情况下，管网分支仍有可能独立工作：因此，为保证管道连通性，对于任一用水节点N，有且只有1个上层水节点N通过管道向其供水，并且G≥G。

以用水节点为决策变量，综合考虑管道长度和管径尺寸，保证管网的管道连通性，提高管网的作业鲁棒性。记树状灌溉管网的水源点0参数为(0,0,E)，用水节点N参数为(x,y,G) (=1,2,…,)。其中，(x,y)为节点地面坐标，G为节点地面高程。对于任一用水节点N，其可用的上层水节点集合S如式(5)所示。

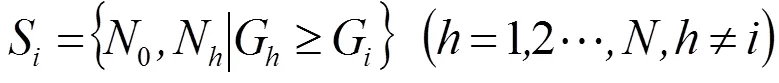
则对于该节点N，一定存在1个上层水节点NϵS，二者连接管道的长度L可通过式(6)得到。

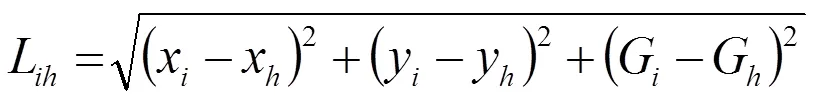
记管道的管径为D，则改进的管网规划模型如式(7)所示。

2　双频蝙蝠算法

2.1　双脉冲频率策略

笔者提出在蝙蝠算法(BA)[16]全局搜索操作中加入双脉冲频率策略，即双频蝙蝠算法(DFBA)。DFBA算法使用双脉冲频率，即1和2分别表征个体最优解和群体最优解对蝙蝠位置更新过程的影响；同时，1和2随当前目标函数的适应值和算法的迭代进程进行参数自适应学习。DFBA算法的全局搜索操作如式(8)、式(9)、式(10)所示。

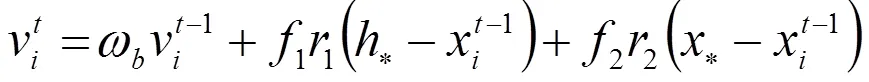
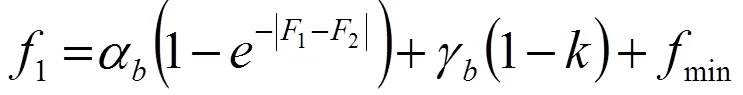
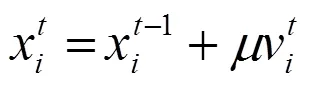
式(8)中：为当前迭代次数；v、x分别表示蝙蝠更新后的速度参数与位置参数；为速度参数的递减权重系数，ω较大，保证了算法前期具有较强的全局搜索能力，ω较小，使算法后期具有较强的局部搜索能力；*为蝙蝠的当前个体最优解；*为蝙蝠群体的当前全局最优解；1和2为(0.5,1.5)范围内的随机数。

式(9)中：1为蝙蝠群体的当前函数适应值均值；2为当前最优蝙蝠个体的函数适应值；=/max为算法迭代进程的评价指数，max为算法最大迭代次数，则ϵ (0,1]；min为常数，用于约束参数1的最小值；参数1主要受目标函数适应值和算法迭代进程的影响，二者权重系数分别为正常数α和ϒ；若记参数1与2之和为常数，则2=–1。随着算法迭代进程变化，参数1取值将从递减为min，参数2取值将从0递增为–min。在算法前期，参数1较大，能够增加蝙蝠群体的多样性，从而增强算法的全局搜索能力；在算法后期，2较大，能够保证算法具有较好的收敛性。

式(10)中：为位置参数的递减权重系数，用于约束蝙蝠全局搜索操作的更新步长，取值范围为(0,1]。

2.2　自适应局部搜索策略

对于蝙蝠，生成随机数βϵ [0,max]，若β<R，则蝙蝠将进行局部搜索操作，如式(11)、式(12)所示。因为脉冲发射频率将随着算法迭代进程变化而增大，则蝙蝠群体在算法后期进行局部搜索操作的概率也将随之增大。

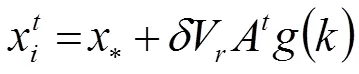
式(11)、式(12)中：*为蝙蝠群体的当前全局最优解；ϵ [–1,1]为随机向量；V为目标函数可行解域的边界距离与蝙蝠群体数量的比值向量，目的是使局部搜索步长随待求解问题的规模自适应变化；A为蝙蝠群体的当前脉冲响度均值。()为随算法迭代进程变化的指数递减函数，用于约束蝙蝠局部搜索操作的更新步长，如式(12)所示。

记蝙蝠群体数量为N，进行局部搜索操作的概率为，则蝙蝠群体单次迭代计算的时间复杂度为O((1+)×N)，其中0<<1。记算法迭代次数为M，则DFBA算法的时间复杂度为O((1+) ×M×N)。

2.3　双频蝙蝠算法性能测试

使用12个测试函数来分析算法性能，如表1所示。其中，1、2、…、5为单峰函数，6、7、…、12为多峰函数。测试环境：Microsoft Windows 7 Pro 64–bit，Intel® Core™ i7–7500U @ 2.70 GHz，8.0 GB RAM，Matlab R2016b。对照GA算法[17]、PSO算法[18]、BA算法[16]、DBA算法[19]、IBA算法[20]的参数设置同原文献。

在DFBA算法中，速度参数权重系数随算法迭代进程变化线性递减，ωmax=0.9，ωmin=0.1；脉冲频率权重系数α=1，ϒ=1.5；双脉冲频率之和=3，min=0.5，max=2.5；位置参数权重系数随算法迭代进程变化线性递减，max=0.7，min=0.3；局部搜索操作函数()的系数为=2，a=2.176 6，1=–2.088 6，2=27.334 9；算法其余控制参数为min=0.3，max=0.7。

各算法种群规模均为50，最大迭代次数均为500次，独立运行50次。基于100维度函数适应值均值的迭代曲线如图1所示，部分结果使用了对数化处理。在单峰函数(1~5)中，PSO算法优于BA算法和GA算法；在多峰函数(6~12)中，BA算法和PSO算法的寻优结果互有优劣。DBA算法在单峰函数中有较好的求解精度，IBA算法在多峰函数(11~12)中表现出一定优势。与对照算法相比，DFBA算法的求解精度和收敛速度均具有较大优势。在多峰函数(6~12)中，DFBA算法曲线出现了不同程度的“陡降”，这主要是因为DFBA算法后期增加了局部搜索操作概率，并且使用较小步长在蝙蝠群体的当前全局最优解附近进行搜索，因而有助于提高算法的求解精度。

表1　测试函数

I~XII分别表示函数f1、f2、…、f12。

3　基于双频蝙蝠算法的树状管网设计

3.1　构建规划模型解空间

管网规划模型决策变量包括用水节点N(=1,2,…,)与上层水节点N(=1,2,…,,≠)之间的连接管道长度L和管道管径D，因此，规划模型的解空间为{L,D}。若管网存在个用水节点，则解空间维度为2。由式(5)、式(6)可知，管道长度L为离散变量，受市场标准限制，管道管径D也为离散变量。由于DFBA算法的变量为连续参数，因此需对算法解空间进行离散化处理。

对于连接管道长度L，需在用水节点N的上层水节点集合S中选择上层水节点N，则在算法解空间中存在对应解xϵ [0,1]，x与N在集合S中序号T的对应关系如式(13)所示。对于管道管径D，在算法解空间中存在对应解xϵ [0,1]，根据式(13)可确定管道管径集合中序号T。

式中：|S|表示集合S中元素数量，||表示集合中元素数量。

由于管网中所有的用水节点均需满足节点压力约束条件，笔者使用罚函数将管网规划模型和约束条件转换为无约束的目标函数，如式(14)所示。

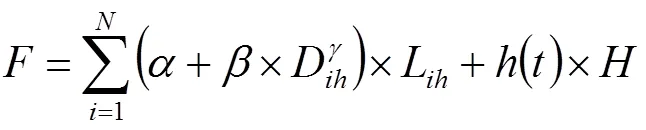
步骤1：初始化树状灌溉管网的节点参数，根据式(5)构建各用水节点的上层水节点集合。若管网中存在多个地面高程相等的用水节点，则分别计算各用水节点与其上层水节点集合的距离均值，均值最小的用水节点将优先成为其他用水节点的上层水节点。

步骤2：初始化DFBA算法参数，构建基于DFBA算法的可行解空间。

步骤3：根据式(8)、式(9)、式(10)计算DFBA算法迭代解；若蝙蝠个体满足局部搜索条件，根据式(11)、式(12)进行算法局部搜索操作。

步骤4：根据式(13)，对DFBA算法的可行解空间进行离散化处理，确定各用水节点的上层水节点及管道管径；根据式(6)，计算连接管道长度，构建管网规划模型可行解空间。

步骤5：根据式(14)，计算管网投资费用，基于函数适应值更新算法的全局最优解。

步骤6：判断是否达到终止条件，如不满足终止条件，则转至步骤3。

3.2　设计案例

分别使用GA算法、PSO算法、BA算法和DFBA算法对管网案例进行设计。管网包括1个水源点和9个用水节点，节点架构同文献[6,9,11–12]。由于提出的管网设计方法通过选择用水节点的上层水节点来保证管网部署的管道连通性，并且使用节点参数自行计算管道连接长度，因而无需使用管网初步连接图。管网节点参数与管道单价如表2所示。在目标函数式(14)中，管道造价参数可通过表3数据的拟合计算得到，即管道造价系数=1.5，=5.37×10–4，管道造价指数=1.92[9,11]；在管网用水节点压力约束式(2)中，局部水头损失系数=1.1，以硬质塑料管材为标准，管道水头损失系数=9.48×104，=1.77，=4.77；各节点的最低水压=10 m；在管道流速约束式(3)中，max=3 m/s，min=0.5 m/s。

表2　10节点管网参数

各算法的种群规模均为50，最大迭代次数均为500次，独立运行50次。各算法基于目标函数式(14)的设计结果，包括管网投资费用最优解、均值和最差解，如表3所示。结果表明，基于PSO算法的设计结果优于GA算法；BA算法在离散组合优化过程中存在易于陷入局部最优的问题。与之相比，基于DFBA算法的管网设计可得到稳定的最优结果，管网投资费用的最优解为20 900元，其均值较BA算法均值减少了23.60%。设计结果表明DFBA算法有效减少了算法陷入局部最优的概率，从而具有良好的算法性能；因此，基于DFBA算法的管网设计方法具有较好的精准性。

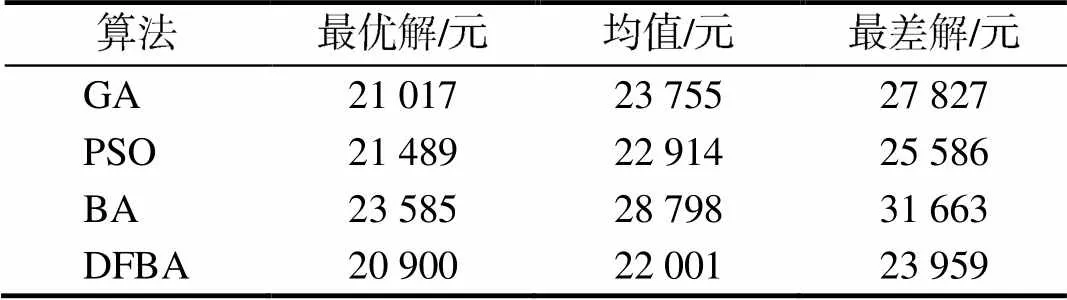
表3　10节点管网各算法的投资费用

使用DFBA算法可得到若干管网最优设计结果，其中之一如图2所示，图中节点架构表明，各用水节点及其对应上层水节点的组合关系，如节点6→7表示节点6为节点7的上层水节点。节点2→3、节点6→4之间的水流流向与原文献[6,9,11–12]中管网节点的初步连接关系不同，这是因为笔者提出的管网规划模型能够根据节点参数自行计算连接关系，设计结果不受管网初步连接图的限制。在计算过程中，得到符合文献管网节点初步连接关系的最优设计结果(图2)所示，管网投资费用最优解为21 585元，均值为24 227元，均值较DFBA算法增加了9.19%。由此说明，笔者提出的设计方法具有更好的通用性。

图2　10节点管网最优设计结果

3.3　扩展案例

由于现有解决方法需使用管网初步连接图，随着管网规模的扩大，即增加管网节点，该项准备工作的难度将随之增大；同时，增加节点使得规划模型的可行解空间呈指数式增大，从而对模型最优解的搜索难度也将随之增大。为进一步验证设计方法的扩展性，扩展案例使用的管网包括1个水源点和33个用水节点，各节点参数如表4所示。

表4　34节点的管网参数

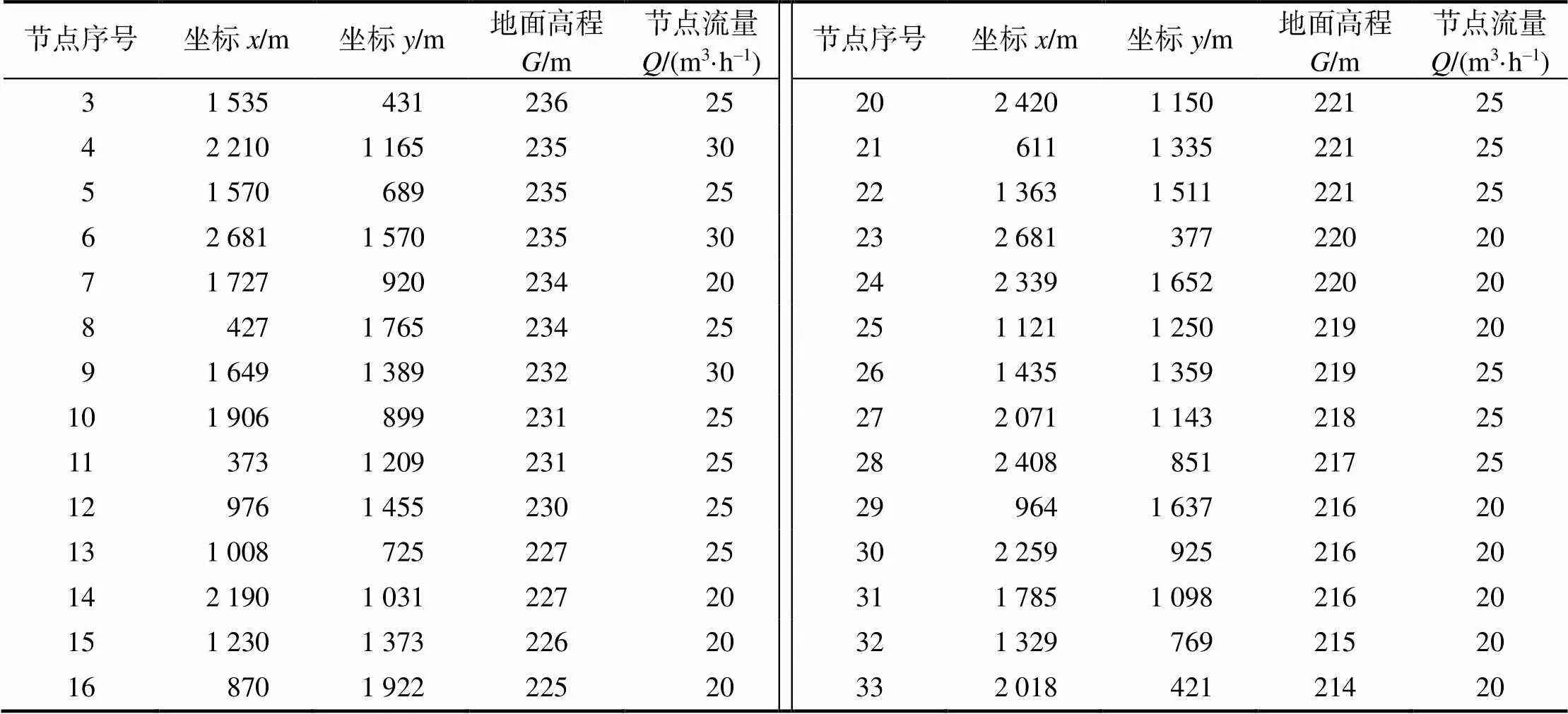
表4(续)

基于各算法的管网投资费用列于表5。基于PSO算法的设计结果优于GA算法和BA算法。与之相比，基于DFBA算法的管网设计仍可得到稳定的最优结果，管网投资费用的最优解为107 091元，其均值较BA算法均值减少了31.03%。表明基于DFBA算法的管网设计方法具有较好的扩展性。为进一步提高设计方法的实用性，笔者设计了一套基于DFBA算法的树状灌溉管网设计软件系统，在输入管网节点参数并设置相关算法参数后，该系统将自动完成管网智能设计过程并输出结果。基于DFBA算法的扩展案例设计结果如图3所示。

表5　34节点管网各算法的投资费用

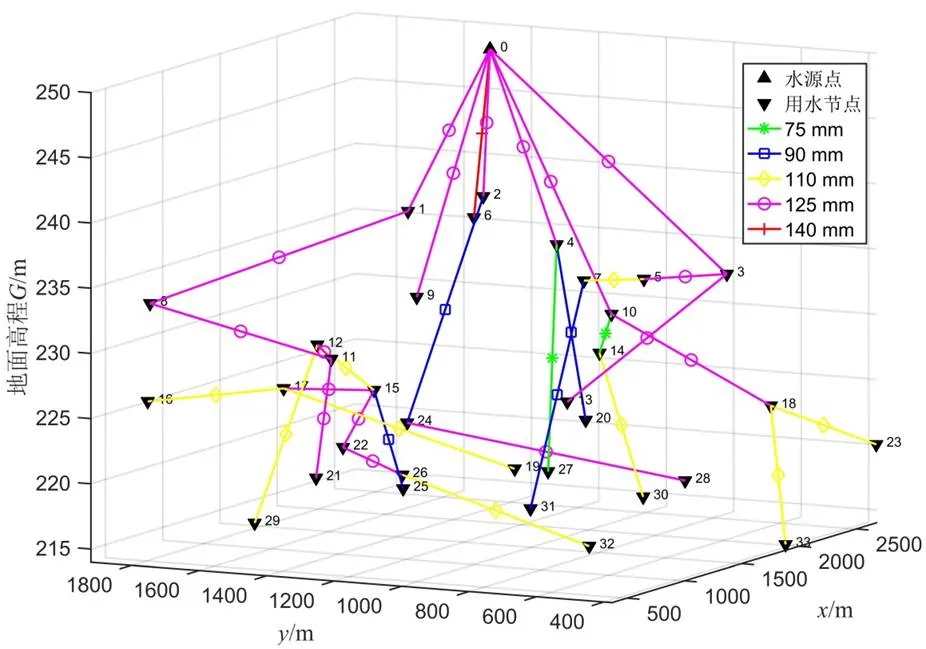
图3　基于DFBA算法的34节点树状灌溉管网

4　结论

笔者提出了改进的自压树状灌溉管网规划模型，并通过2个不同拓扑结构的管网案例验证了基于DFBA算法的管网设计方法的有效性。研究结果表明：改进管网规划模型，能够通过对用水节点与上层水节点的不同组合来保证树状灌溉管网的管道连通性，不需要使用管网初步连接图，具有较好的通用性与扩展性。

测试函数验证了基于双频脉冲策略的DFBA算法具有较好的全局搜索能力和寻优精度，管网案例验证了基于DFBA算法的管网设计方法能够有效减少管网投资费用，具有较好的实用性。

树状灌溉管网规划设计问题较为复杂，单一模型难以全面描述管网的多变性特点。提出的设计方法能够在使用不同规划模型的情况下，应用DFBA算法，通过寻找用水节点及其对应上层水节点的最佳组合来自行完成设计过程。后续将进一步研究基于不同部署形式的规模化灌溉管网智能规划作业方法。

[1] ALEXIOU D，TSOUROS C．Design of an irrigation network system in terms of canal capacity using graph theory[J/OL]．Journal of Irrigation and Drainage Engineering，2017，143(6)：06017002．

[2] 杨建军，战红，丁玉成．基于圈的单水源树状管网优化改进遗传算法[J]．排灌机械工程学报，2010，28(2)：164–168． YANG J J，ZHAN H，DING Y C．Improved genetic algorithm for optimization of single source tree-type pipe network based on cycle[J]．Journal of Drainage and Irrigation Machinery Engineering，2010，28(2)：164–168．

[3] 马雪琴，吕宏兴，朱德兰，等．基于遗传算法的树状灌溉管网优化设计[J]．中国农村水利水电，2013(4)：50–52． MA X Q，LYU H X，ZHU D L，et al．Tree-type pipe network optimization design based on genetic algorithm[J]. China Rural Water and Hydropower，2013 (4)：50–52．

[4] 马朋辉，李援农，胡亚瑾，等．基于和声搜索算法的自压式树状管网优化设计[J]．中国农村水利水电，2016 (6)：14–18． MA P H，LI Y N，HU Y J，et al．Optimal design of gravity tree-type pipe network based on harmony search algorithm[J]．China Rural Water and Hydropower，2016 (6)：14–18．

[5] 周荣敏，林性粹．压力输水树状管网遗传优化布置和神经网络优化设计[J]．农业工程学报，2002，18(1)：41–44． ZHOU R M，LIN X C．Genetic optimization layout and artificial neural networks optimal design of pressurized tree water-pipe network[J]．Transactions of the Chinese Society of Agricultural Engineering，2002，18(1)：41–44．

[6] 周荣敏，雷延峰．基于改进单亲遗传算法的树状管网布置优化[J]．水利学报，2012，43(10)：1243–1247． ZHOU R M，LEI Y F．Optimal layout of tree pipe networks based on improved single parent genetic algorithm[J]. Journal of Hydraulic Engineering，2012，43(10)：1243–1247．

[7] 王新坤．基于不可行度的机压树状管网退火遗传算法优化[J]．农业机械学报，2009 (9)：63–67． WANG X K．Optimization of pumping tree pipe network by using annealing-genetic algorithms based on infeasible degree[J]．Transactions of the Chinese Society of Agricultural Machinery，2009 (9)：63–67．

[8] BABU K S J，VIJAYALAKSHMI D P．Self-adaptive PSO–GA hybrid model for combinatorial water distribution network design[J]．Journal of Pipeline Systems Engineering and Practice，2012，4(1)：57–67．

[9] 马孝义，范兴业，赵文举，等．基于整数编码遗传算法的树状灌溉管网优化设计方法[J]．水利学报，2008，39(3)：373–379． MA X Y，FAN X Y，ZHAO W J，et al．Tree-type pipe network optimization design method based on integer coding genetic algorithm[J]．Journal of Hydraulic Engineer- ing，2008，39(3)：373–379．

[10] 杨建军，丁玉成，赵万华．基于双重编码遗传算法和图论的自压树状管网优化[J]．农业机械学报，2010，41(1)：81–85． YANG J J，DING Y C，ZHAO W H．Optimization of Gravity tree-type pipe network based on dual codeing genetic algorithm and graph theory[J]．Transactions of The Chinese Society of Agricultural Machinery，2010，41(1)：81–85．

[11] 李海滨，马孝义，赵文举，等．树状管网布置与管径同步优化方法研究[J]．系统仿真学报，2009，21(11)：3180–3183． LI H B，MA X Y，ZHAO W J，et al．Layout and diameter simultaneous optimization method of tree pipe network[J]. Journal of System Simulation，2009，21(11)：3180–3183．

[12] IBRAHIM M，LI H B，LIU Y，et al．Optimization of tree pipe networks layout and size，using particle swarm optimization[J]．Wseas Transactions on Computers，2014，13：219–230．

[13] 邱金亮，王静，左传英，等．基于组合遗传算法的树状管网整体优化设计模型[J]．中国农村水利水电，2013 (9)：26–28，32，36． QIU JL，WANG JJ，ZUO C Y，et al．Tree pipe network optimization design method based on combined genetic algorithm[J]．China Rural Water and Hydropower，2013 (9)：26–28，32，36．

[14] 朱成立，谢志远，柳智鹏．基于蚁群算法的灌溉管网布置与管径优化设计研究[J]．江西农业学报，2015，27(3)：93–96． ZHU C L，XIE Z Y，LIU Z P．Research on layout of irrigation pipe network and optimized design of pipe diameter based on ant colony algorithm[J]．Acta Agriculturae Jiangxi，2015，27(3)：93–96．

[15] AFSHAR M H，AKBARI M，MARIÑO M A. Simultaneous layout and size optimization of water distribution networks：engineering approach[J]．Journal of Infrastructure Systems，2005，11(4)：221–230．

[16] YANG X S，HOSSEIN G A．Bat algorithm：a novel approach for global engineering optimization[J]. Engineering Computations，2012，29(5)：464–483．

[17] PARSOPOULOS K E，VRAHATIS M N．Particle swarm optimization method for constrained optimization problems[J]. Intelligent Technologies-Theory and Applica- tion：New Trends in Intelligent Technologies，2002，76(1)：214–220．

[18] DAMOUSIS I G，BAKIRTZIS A G，DOKOPOULOS P S. Network-constrained economic dispatch using real-coded genetic algorithm[J]．IEEE Transactions on Power Systems，2003，18(1)：198–205．

[19] CHAKRI A，YANG X S，KHELIF R，et al. Reliability-based design optimization using the directional bat algorithm[J]．Neural Computing and Applications，2018，30(8)：2381–2402．

[20] WANG G G，CHU H C E，MIRJALILI S. Three- dimensional path planning for UCAV using an improved bat algorithm[J]．Aerospace Science and Technology，2016，49：231–238．

[21] ROBINSON J，RAHMAT-SAMII Y．Particle swarm optimization in electromagnetics[J]．IEEE Transactions on Antennas and Propagation，2004，52(2)：397–407．

Planning of tree-type irrigation pipe network based on the dual-frequency bat algorithm

LYU Shilei1,2, LU Sihua1, WEI Zhiwei1, LI Zhen1,2*, WU Benlei1

(1.College of Electronic Engineering, South China Agricultural University, Guangzhou, Guangdong 510642, China; 2.Division of Citrus Machinery, China Agriculture Research System, Guangzhou, Guangdong 510642, China)

An improved planning model of tree-type irrigation pipe network is proposed with the purpose of minimizing the expenditure of construction. Pipeline connectivity is guaranteed by using the concept of high-level nodes. Meanwhile, an improved dual-frequency bat algorithm(DFBA) is proposed to balance the diversity and convergence of the proposed algorithm by dual-frequency strategy. The optimization 100 dimension results of 12 test functions indicate that the DFBA can enhance global search capability effectively in comparison to the genetic algorithm, the particle swarm optimization algorithm and the original bat algorithm. Finally, planning experiments are performed on 2 pipe network cases, which consist of 10 nodes and 34 nodes respectively. Compared to the original bat algorithm, the mean values of investment cost obtained using the DFBA can be reduced by 23.60% in the pipe network of 10 nodes, and 31.03% in the pipe network of 34 nodes, respectively.

tree-type pipe network; pipe network layout; dual-frequency bat algorithm

10.13,331/j.cnki.jhau.2020.01.015

TP301.6; S274.2

A

1007-1032(2020)01-0099-08

2019–08–22

2019–10–03

国家自然科学基金项目(61601189，31971797)；现代农业产业技术体系建设专项(CARS–26)；广东省科技计划项目(2016A020210088)；广州市科技计划项目(201803020037)

吕石磊(1984—)，男，河北石家庄人，博士，副教授，主要从事农业信息化研究，lvshilei@scau.edu.cn；

，李震，博士，教授，主要从事机电一体化技术应用研究，lizhen@scau.edu.cn

吕石磊，卢思华，魏志威，李震，吴奔雷．基于双频蝙蝠算法的树状灌溉管网规划[J]．湖南农业大学学报(自然科学版)，2020，46(1)：99–106．

LYU S L, LU S H, WEI Zhiwei, LI Z, WU B L. Planning of Tree-type irrigation pipe network based on the dual-frequency bat algorithm[J]．Journal of Hunan Agricultural University(Natural Sciences), 2020, 46(1): 99–106.

http://xb.hunau.edu.cn

责任编辑：罗慧敏

英文编辑：吴志立