基于TensorFlow 手写体数字识别系统的研究

李建新

（广州工商学院 计算机科学与工程系，广州528138 ）

0 引言

目前，手写体数字识别是人工智能机器学习领域众多研究者关注的一个热点，广泛应用于公安、税务、交通、金融、教育等行业的实践活动中。在实际应用中，对手写数字单字识别率的要求比手写普通文字识别要苛刻许多，识别精度需要达到更高的水平。由于手写数字识别没有文字识别那样的上下文，不存在语意的相关性，而数据中的每一个数字又至关重要。因此，提高手写数字识别率，成为人工智能的重要研究领域。

人工神经网络是一种类似于大脑神经突触联接的结构，进行信息处理的数学模型，具有学习和记忆功能，可以让神经网络学习各个模式类别中的大批量训练样本，记忆各个模式类别中的样本特征。在识别样本时，将逐个与记忆中各模式类别的样本特征相比较，从而确定样本所属类别。人工神经网络通过学习调整内部大量节点之间相互连接的关系，可获得众多优化的模型参数。

1 手写体数字识别系统

1.1 系统组成

手写体数字识别系统由输入、预处理、识别等环节组成，系统架构如图1 所示。

输入环节包括MNIST 手写体数据集输入和用户预测图片里的手写体数字；预处理环节主要指用户手写体数字预测图片的预处理；识别环节包括卷积神经网络、分类识别器、损失函数和优化器。卷积神经网络实现数字手写体0～9 特征提取，分类识别是手写体数字识别最关键的部分。经过卷积神经网络提取来的特征被送到分类器中，对其进行分类识别。分类识别器由softmax 完成，softmax 得到当前样例中属于不同种类的概率分布情况。

优化器在神经网络训练和测试过程中，根据计算结果与损失函数要求，调节模型可变参数，让神经网络参数尽快达到理想误差范围。

1.2 MNIST 数据集训练与测试

训练一个卷积神经网络时，需要大量的数据、设置卷积的层数、卷积核大小、池化的方式（最大、平均）、损失函数、设置目标（如：手写数字的识别，输出一个10 维向量）等，让卷积神经网络通过不断的训练更新参数，向设置的目标靠近，最后可以通过这些参数来预测样本。

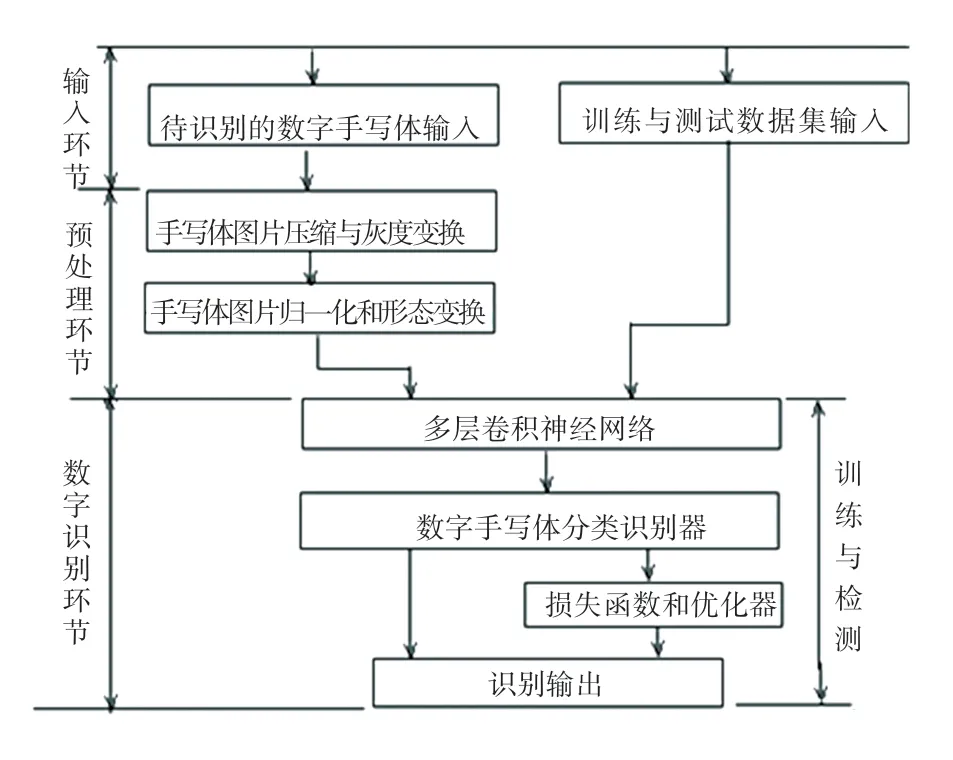
图1 手写体数字识别系统组成Fig.1 Composition of handwritten digit recognition system

通常情况下，假设样本由K个类组成，共有m个，则数据集可由式（1）表示：

式中，x（i）∈R（n +1）；y（i）∈｛1，2，…，K｝，n +1 为特征向量x的维度。

MNIST 是机器学习中的一个数据集，包含0～9的不同人手写数字图片。数据集由60 000 个手写数字训练样本和10 000 个手写数字测试样本组成，每个样本是一张28 * 28 像素的灰度手写数字图片。则MNIST 数据集的训练集m＝60 000，n +1＝784，K＝10、MNIST 数据集的测试集m＝10 000，n+1＝784，K＝10；分别由式（2）、式（3）表示为：

机器学习模型设计时，将提供大量的数据以训练一个手写体数字的机器学习，所得到的模型参数，最终用于预测用户图片里面的数字。

1.3 卷积神经网络与分类器

卷积神经网络是系统的核心部分，是由输入层、多个卷积层、多个池化层、多个全连接层以及输出组成的多层感知器。卷积层为局部连接，用于提取图像特征；池化层用于进一步降低输出参数数量，提高了模型的泛化能力；全连接层进行特征关系和权重值计算，完成分类处理。手写体数字识别卷积神经网络的组成示意如图2 所示。

在TansorFlow 中卷积层、池化层和全连接层部分代码如下：

图2 手写体数字识别卷积神经网络组成Fig.2 Composition of convolution neural network for handwritten digit recognition

为了提高卷积神经网络对手写体数字识别的准确率，可以通过多种途径来实现。如：增加卷积层数量，以便进行更高层次的特征提取；改变各卷积层的卷积核大小，以便调整特征提取范围，或改变卷积步长；增加卷积层中卷积核的数量，意味着提取特征图的数量（一个卷积核卷积出来一个特征图），也就意味着可以从更多的角度提取原图的特征，避免视角单一，卷积出来多个特征图后要重新组织输出形态，用以适应下一层的输入要求。

分类器采用Softmax 回归算法，该算法能将二分类的Logistic 回归问题扩展至多分类。Softmax 回归算法对于给定的输入值x（i），输出的K个估计概率可由式（4）［1］表示：

其中，K为类别的个数，和bi为第i个类别对应的权重向量和偏移向量，在TensorFlow 中用张量表示。

上述Softmax 回归算法在TansorFlow 中的相应代码如下：

1.4 损失函数和优化器

通常采用的损失函数“交叉熵”（cross -entropy），如式（5）［2］所示：

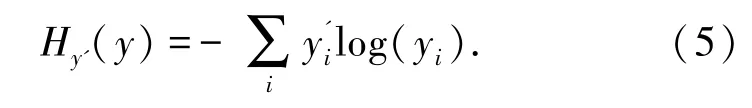
式中，y为预测概率的分布，y＇ 为实际样本的标签值。

TensorFlow 中提供了8 种优化器，即BGD、SGD、Momentum、Nesterov Momentum、Adagrad、Adadelta、RMSprop 和Adam，模型训练一般采用梯度下降优化器。

在TansorFlow 中，损失函数、学习率为learning_rate 的优化器代码［2］如下：

由以上系统组成可知，MNIST 数据集、卷积神经网络与分类器、损失函数和优化器是人工神经网络学习模型训练机制的组成部分。

2 用户手写体数字识别

通过对MNIST 数据集的训练和测试，模型参数达到要求并予以保存。在用户实际应用时可以导入模型参数对用户手写数字识别。由于MNIST 数据集手写数字以张量形式存在，其形态为1 维［784］，而用户手写数字可以各种像素的数字图像存在，故用户手写数字在识别前需要将其图像进行预处理，需与MNIST 数据集28×28 像素达到一致。

2.1 数字预处理

预处理对于系统设计非常重要，经过预处理后的图像才能进行特征提取。因此，预处理的好坏直接影响着识别结果。因导入的点阵图形大小各异，需将点阵图形压缩成与MNIST 数据集中的大小相一致，调整用户手写数字灰度图像形态为［28，28］；随后将用户手写数字图像转换为灰度图像。灰度图像像素值纯黑色的灰度级别为0，纯白色的灰度级别为255，介入两者之间还有许多灰度级别。由于MNIST 数据集图片像素纯白色～纯黑色采取正规化的0～1 区间，故用户手写数字灰度图像也须进一步正规化到0～1 区间。用户手写数字预处理流程如图3 所示。

图3 用户手写数字预处理流程Fig.3 Preprocessing process and code of handwritten digits

经处理后的数字图片格式与MNIST 数据集的图片格式相同，则可将图片输入到网络中进行识别。

2.2 检测用户手写数字图像的神经网络

对用户手写数字图像进行检测的卷积神经网络，与MNIST 数据集的训练和测试的卷积神经网络结构相同。模型参数为MNIST 数据集的训练与测试得到并保存模型参数，主要是卷积神经网络的各层参数。只要恢复、使用之前保存的模型参数，用这些已知的参数构建卷积神经网络，通过其将用户手写数字图像从卷积神经网络输入，以完成到输出的映射，获得相应数字。

2.3 数字识别实现

TensorFlow 是一个开源的机器学习框架，在图形分类、音频处理、推荐系统和自然语言处理等场景下有着丰富的应用，并提供了多种编程语言的接口。本系统建立在TensorFlow 平台上，分二部分完成：

2.3.1 建立模型参数

（1）导入MNIST 数据集，并构建卷积神经网络学习模型；

（2）对学习模型进行训练和测试；

（3）评价学习模型是否为最佳模型参数，是则保存模型参数，否则修改学习模型，继续执行（2）、（3）步骤。

2.3.2 用户手写数字识别

（1）数字预处理，以使用户手写数字与MNIST数据集一致；

（2）使用保存的模型参数构建用户手写数字识别模型；

（3）用户手写数字输入手写数字识别模型，得到用户手写数字输出。

3 实验数据分析

实验分为无卷积神经网络和有卷积神经网络。实验以损失函数、训练数据准确率和测试数据准确率为参考，见表1。

表1 训练损失值与数据准确率Tab.1 Training loss and data accuracy

由表1 中上半部数据可知，随着学习率的增加，损失函数值的减少，训练准确率和测试准确率均增加，但学习率增加过大。如，学习率为1.0 和1.5 时，导致数据准确率发生振荡。

由表1 中下半部数据可知，当学习率小于0.65时，前20 轮训练损失函数收敛很快，训练准确率和测试准确率很快达到0.98 以上，最高为1。学习率过大，如0.75，损失函数找不到最小点，无法收敛，甚至出现未定义或不可表示的值。

4 结束语

通过实验比较了无卷积和卷积在神经网络中的作用，对学习训练参数、优化器也做了比较，取得了相应数据，学习率大小对无卷积神经网络影响为引起数据准确率发生振荡，对有卷积神经网络影响为引起损失函数找不到最小点，数据准确率大幅度下降。在学习率大小合适条件下有卷积神经网络的损失值和学习率均明显优于无卷积神经网络，实验结果挖掘了神经网络对图形内在的特性。

本研究是手写体数字识别系统开发的组成部分，其成果对整个系统开发工作奠定了很好的基础。