一种基于蝙蝠算法的多目标跟踪数据关联方法

王宇杰，李 宇，黄海宁

(1. 中国科学院声学研究所，北京100190；2. 中国科学院先进水下信息技术重点实验室，北京100190；3. 中国科学院大学，北京100049)

0 引 言

数据关联问题一直是多目标跟踪方法中关键性的问题，它决定了目标更新时所使用的探测信息，所以数据关联算法的性能直接决定了多目标跟踪算法的跟踪性能。国内外学者对数据关联的方法进行了深入的研究，其中最早提出的数据关联方法是最近邻算法 (Nearest Neighbor, NN)[1]，它直接将量测与距离最近的目标关联，方法简单，运算量小，但在处理多目标关联问题时，关联正确率低。在理想化的建模假设下，多假设跟踪算法 ( Multiple Hypothesis Tracking, MHT)[1-3]被认为是在贝叶斯角度的最优方法，但当目标数目增加时，它需要很大的计算量和内存。概率数据关联算法(Probabilistic Data Association, PDA)[1,3]计算落入目标跟踪门内的所有量测的关联概率，依据概率进行关联，但在目标数目增加时，PDA 难以满足关联性能要求。在此基础上发展出的联合概率数据关联算法 (Joint Probabilistic Data Association,JPDA)[3]将PDA 推广到了多个目标的情况，使用所有观测值和所有目标进行概率计算，是对多目标进行跟踪的比较优秀的方法，但是需要的计算量极大。

数据关联问题和组合优化问题具有很高的类似度，对多目标数据关联问题建模，演化为组合优化问题，再利用一些智能优化算法进行最优估计是解决多目标数据关联问题的一个方向[4-5]，一些仿生优化算法[6]在多目标关联领域也取得了较好的效果。蝙蝠算法(Bat Algorithm, BA)[7-9]是Yang于2010 年提出的一种仿生优化算法，近几年蝙蝠算法已经在很多领域取得了应用。本文通过对数据关联问题进行建模，并对蝙蝠算法的搜索更新规则进行改进，提出了一种适用于数据关联的改进蝙蝠算法(Bat Algorithm Data Association,BADA)，使其可以成功应用于数据关联问题。经过仿真验证，改进的蝙蝠算法应用于数据关联切实可行，并且有比较好的效果，在计算复杂度上也远低于传统算法。

1 数据关联优化形式

(1) 对于每一个量测，最多只有一个目标与其关联。

(2) 对于每一个目标，也只有一个量测与其关联。

数据关联的目标函数可以表示为

式中：gi,j表示目标i 和量测j 的关联程度；uij为目标i 和量测j 关联情况。

由上述两个假设得到的约束条件为

由uij组成关联矩阵U，uij的值为0 或1，当量测与第i 个目标关联时，uij为1，否则为0，u0j表示第j 个量测来源于杂波信号。关联矩阵U 的表达式为

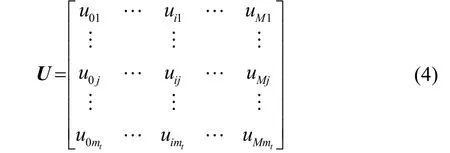
对于量测与目标之间的关联程度gi,j，本文使用似然函数来评价：

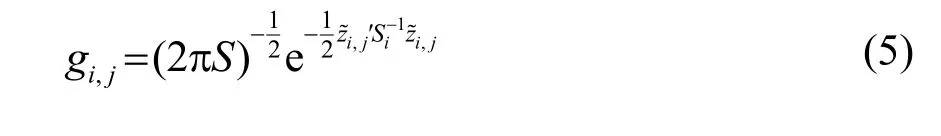
其中：

式(5)、(6)中：zi表示第i 个目标该时刻的预测值；yj表示第j 个目标的测量值。t 时刻目标一步预测的状态矩阵为，S 表示残差。

当目标的预测值和目标该时刻回波正确关联时，则似然函数gi,j的值最大。在理想情况下，当所有目标的预测值都和目标该时刻的回波正确关联，则目标函数J 的值最大。所以，通过将数据关联问题建模成组合优化问题，最大化目标代价函数J，可以解决数据关联问题。

2 蝙蝠算法描述

蝙蝠算法是模仿蝙蝠回声定位系统提出的一种仿生算法。在自然界，蝙蝠通过向四周发射超声波脉冲进行捕猎和定位。在接收到回波之后，它们可以确定自己的位置，并且发现周围的猎物和障碍。再者，在蝙蝠群中，每一只蝙蝠都可以通过独立搜索发现最有营养的区域，或者和种群中其它个体交流，向其它个体发现的最有营养的区域移动。蝙蝠算法最重要的思想是蝙蝠的定位系统运作方式，为了对其有一些合适的调整，Yang 提出了以下规则[7-9]：

(1) 所有的蝙蝠都使用回声定位系统对目标位置进行探测，并且可以区分猎物和障碍。

(2) 所有的蝙蝠在一定的位置以一定的速度随机飞行去搜索目标，它们发射的声波频率、声强和声脉冲发射频率以一定的规律变化。在理想化的规则里，假设每一个蝙蝠都可以自动地调整声波频率和脉冲发射的频率，这种自动调节系统依据离目标猎物的远近进行调节。

(3) 在真实的环境中，蝙蝠发声声强的变化可以依据多种方式。而我们假设声强是从最大声强向最小的声强变化。

由上述规则，Yang 提出的经典蝙蝠算法，算法如下：

(1) 定义目标函数ξ ( x)；

(3) 对蝙蝠群中的每一只蝙蝠的位置xi进行步骤(4)；

(5) 对蝙蝠群中的每一只蝙蝠位置ix 进行步骤(6)～(11)；

(6) 使用式(7)、(8)、(9)产生新的蝙蝠位置；

(8) 本地搜索：在最优蝙蝠位置附近更新该只蝙蝠；

(10) 接受该蝙蝠为当前最优蝙蝠x∗；

(12) n=n+1；

(13) 循环执行步骤(5)～(12)，直至达到结束条件；

(14) 排序蝙蝠群中的蝙蝠，输出最优蝙蝠位置x∗。在步骤(7)、(9)中rand[0,1]表示取0～1 之间的随机数。

在每一次循环中，蝙蝠群中的每一只蝙蝠都会进行移动，对于每次移动，使用式(7)～(9)进行更新：

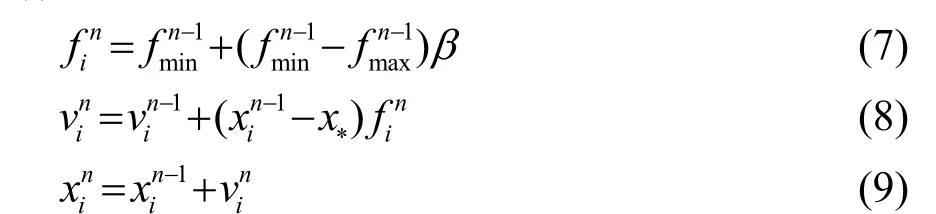
其中：β 是一个0～1 之间的随机数；在算法流程中x∗是蝙蝠群中当前时刻最优蝙蝠位置；和代表了第i 只蝙蝠在第n 次迭代中的速度和位置。式(7)被使用来限制蝙蝠移动的范围和速度。算法流程中第(8)步本地搜索部分，是从当前时刻蝙蝠群中选择最优蝙蝠，使用随机漫步在最优蝙蝠附近生成新的蝙蝠方案更新该只蝙蝠。

这里 的α 和γ 是固定值，并且0＜α ＜1 ，γ＞ 0。从式(10)和(11)中可以看出，随着n 趋向于无穷大时，趋向于0，趋向于。在很多文章中，为了简化算法，α 和γ 的取值一般是相同的，在0.90～0.99 范围内，本文选取α =γ = 0.98。

3 适用于数据关联的蝙蝠算法

经典蝙蝠算法主要用于解决连续性优化问题，而组合优化问题是一种离散优化问题。受蝙蝠算法解决旅行商问题(Traveling Salesman Problem, TSP)[10]的启发，需要对经典蝙蝠算法进行一些改进，以使其可以适用于数据关联问题。

在本文所提出的算法中，蝙蝠群的每一只蝙蝠都代表一种可能的关联方案。比如某时刻存在4个目标，传感器探测到了9 个量测，则蝙蝠群中的第i 只蝙蝠位置可能为xi= (2,5,3,9)，其第一个位置的2 表示第二个量测和第一个目标关联，其余类似。经典蝙蝠算法中的一些参数ri、 Ai、fi和iv 也并不都适用于离散的数据关联，需要进行一些新的定义。

在经典的算法中，速度vi的更新由声波频率if 和该蝙蝠与最优蝙蝠之间的距离共同决定，如式(8)所示，其显然是无法应用于离散的数据关联问题。从式(8)中可以看出，速度的大小是依赖于该蝙蝠与最优蝙蝠之间的距离再乘上一个系数，声波频率fi。针对数据关联问题，本文对其进行了调整，使用汉明距离DHamming来定义两只蝙蝠的距离，定义该蝙蝠的速度为1 到汉明距离之间的一个随机整数，表达式为

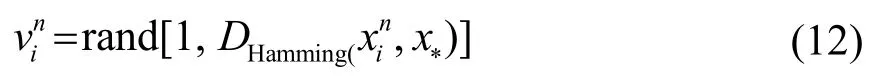
式中，rand[]⋅表示取随机数。

式(9)是蝙蝠算法中蝙蝠的更新运算，该式同样无法应用于数据关联问题中，本文定义运算⊕进行蝙蝠的更新，公式为

运算⊕参照以下规则进行：

(1) 如某一蝙蝠为(2,5,3,9)，首先随机确定一个位置，比如第三个位置，然后随机生成一个量测编号，比如4，使用新生成的量测编号代替原来位置的量测编号，则该只蝙蝠的邻近蝙蝠就是(2,5,4,9)。

(2) 如果随机产生的量测编号发生重复，比如第三个位置随机生成的量测编号为2，而(2,5,2,9)不满足前文提出的第二条假设。这时对调产生重复的两个量测编号的位置，则该只蝙蝠的邻近蝙蝠就是(3,5,2,9)。

使用上述提出的产生邻近蝙蝠位置的方法，在每一次迭代过程中，产生个该蝙蝠的邻近蝙蝠，在其中选择最优的一只更新位置，得到位置。

下面给出了适用于数据关联的改进后的蝙蝠BADA 算法如下：

(1) 使用式(1)定义目标函数J ( x )；

(3) 对蝙蝠群中的每一只蝙蝠ix 进行步骤(4)；

(5) 对蝙蝠群中的每一只蝙蝠位置ix 进行步骤(6)～(11)；

(6) 使用式(12)、(13)产生新的蝙蝠；

(8) 本地搜索：在最优蝙蝠位置附近更新该只蝙蝠位置；

(10) 接受该蝙蝠位置为最优蝙蝠位置x∗；

(12) n=n+1；

(13) 循环执行步骤(5)～(12)，直至达到结束条件；

(14) 排序蝙蝠群中的蝙蝠位置，输出最优蝙蝠位置x∗。

结束条件一般为目标函数达到要求或者循环次数到达预设值。在本文中，设置当循环次数n达到15 次时，算法结束，排序蝙蝠群中的蝙蝠位置，输出的最优蝙蝠位置x∗为最终的数据关联结果。

4 仿真实验与实测数据处理

4.1 仿真实验

为验证BADA 算法的性能，仿真了双目标情况下的方位历程信息。两个目标起始方位分别为250°和280°，在65 s 附近发生了一次交叉，如图1 所示。图1 中圆圈和三角分别表示目标1 和目标2 的回波，干扰回波没有在图中体现。设检测概率Pg=0.95，干扰回波在观测门限内均匀分布，杂波密度为0.1，目标回波服从正态分布，存在均值为0，标准差为0.6 的加性高斯白噪声，使用卡尔曼滤波进行跟踪。用NN 算法和JPDA 算法进行对比，结果如图2 所示。JPDA 算法和BADA 算法在两个目标发生交叉时都可以进行正确的关联，而NN 算法在目标发生交叉时，发生关联错误的概率较大。

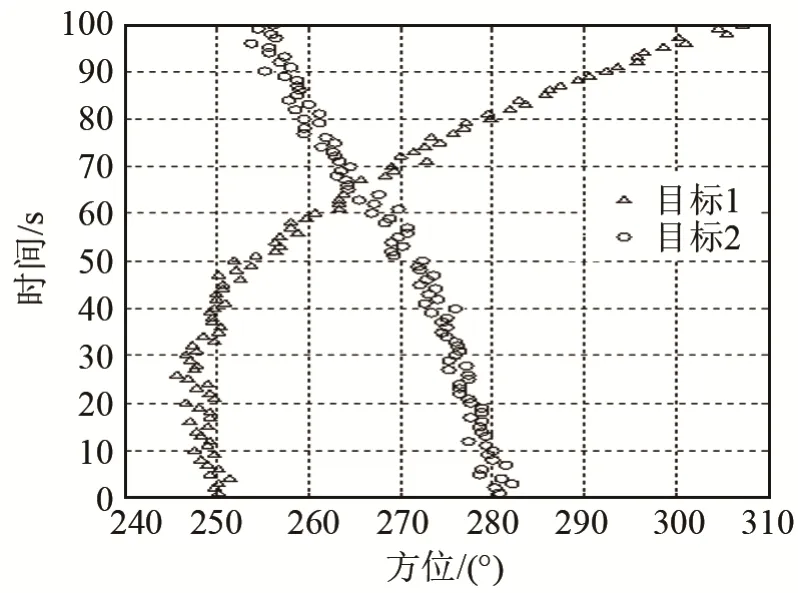
图1 两目标回波仿真数据Fig.1 Echo simulation data of two targets

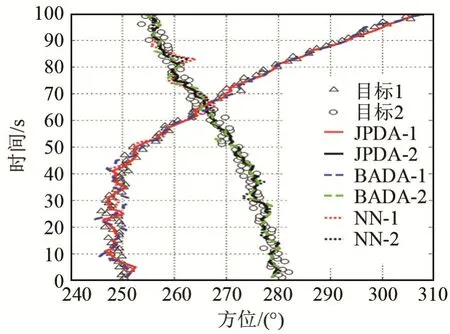
图2 NN 算法、JPDA 算法和BADA 算法仿真结果比较Fig.2 Comparisons between the simulation results of NN algorithm, JPDA algorithm and BADA algorithm

分别使用BADA 算法、JPDA 算法和NN 算法进行1 000 次的独立重复试验，统计其平均绝对误差、平均运算时间和正确关联概率。一次正确的关联为两个目标的跟踪结果始终保持在目标真实位置的附近，如图2 中JPDA 算法和BADA 算法的结果，而NN 算法对于目标2 的跟踪在交叉时发生了错误。两个目标中只要存在一个目标发生关联跟踪错误，即认为关联跟踪错误。正确关联概率使用式(14)计算：

其中：η 为正确关联概率；l 为正确关联跟踪次数；K 为独立重复试验总数，本文中取1 000 次。

在当高斯噪声均值为0、标准差为0.3 时的情况下，3 种算法都有很高的正确关联概率，NN 算法的运算时间最短，误差最大，比较结果列于表1中。当高斯噪声均值为0、标准差为0.6 时算法性能比较结果见表2。BADA 算法在误差和正确关联概率与JPDA 算法相近的情况下，运算时间极大的减小，而NN 算法虽然运算时间极快，但其误差较大，正确关联概率过低，在应用中会出现大量的关联错误。

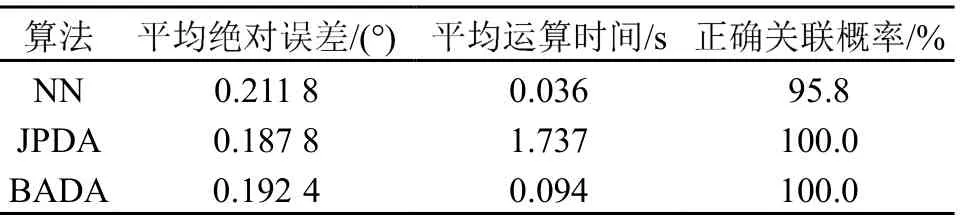
表1 双目标情况下3 种算法性能比较(噪声标准差=0.3)Table 1 Performance comparison of three algorithms in the case of two targets ( noise standard deviation = 0.3)

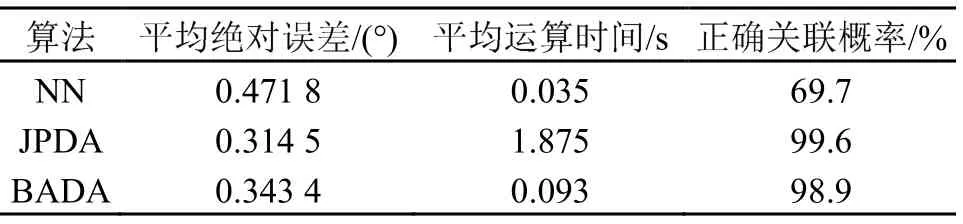
表2 双目标情况下3 种算法性能比较(噪声标准差=0.6)Table 2 Performance comparison of three algorithms in thecase of two targets ( noise standard deviation = 0.6)

为验证更为复杂情况下的算法性能，仿真了同时存在6 个目标的方位历程数据，6 个目标发生了多次交叉，复杂度较高。图3 是使用BADA 算法的关联跟踪结果，不同标记分别代表不同目标的回波。干扰回波在观测门限内均匀分布，杂波密度为0.1，目标回波服从正态分布，存在均值为0，标准差为0.35 的加性高斯白噪声，干扰回波同样存在但未在图中体现，不同颜色的轨迹是使用BADA 算法对不同目标进行关联跟踪的结果。可以看出在轨迹更为复杂的多目标情况下，BADA算法对6 个目标进行了准确的关联，未出现关联跟踪错误。

图3 基于BADA 算法六目标跟踪结果Fig.3 Tracking results of six targets based on BADA algorithm

同样，用上述的6 个目标方位仿真数据，分别对BADA 算法、JPDA 算法和NN 算法进行1000 次独立、重复试验，计算3 种算法的平均绝对误差、平均运算时间和正确关联概率。在正确关联概率的计算中，只要有一个目标关联错误即为错误关联。算法性能比较结果见表3，BADA 算法的运算时间相较于JPDA 算法有了明显的降低，只有不到后者的10%，具有更好的实时运算性能，且正确关联概率也处于较高水平。

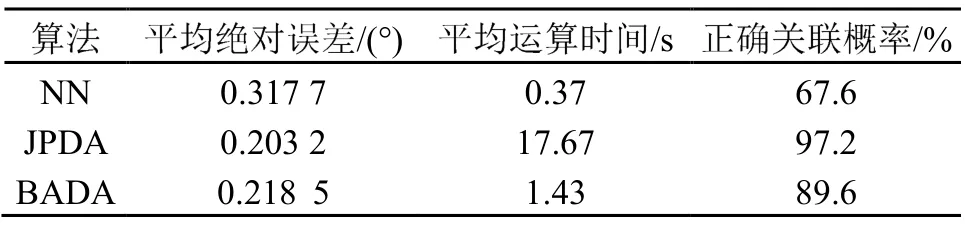
表3 6 个目标情况下3 种算法性能比较Table 3 Performance comparison of three algorithms in the case of six targets

4.2 实测数据处理

图4 是对某次海试的某段数据进行频域波束形成之后的结果。在这段时间内存在多个目标并且目标的方位轨迹之间存在交叉、平行和逐渐靠近，也存在有大量的干扰和噪声，复杂度极高，且具有一定代表性。阈值检测之后使用BADA 算法进行关联跟踪，结果如图5 所示。图5 中白色圆圈是对方位历程图进行阈值检测的结果，阈值检测过程中每10 s 得到一个方位检测结果，不同颜色分别代表不同目标的跟踪结果。

由图5 可见，BADA 算法对6 个较强目标进行了正确的关联，在复杂轨迹情况和干扰回波影响下都没有发生关联跟踪错误。

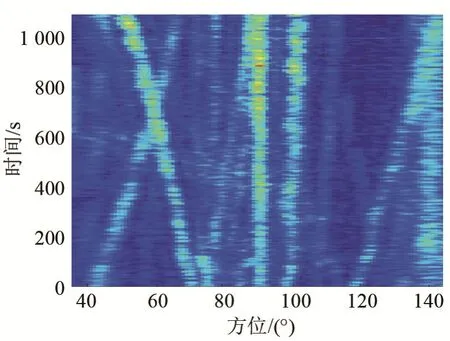
图4 某次海试的某段方位历程图Fig.4 A section of bearing-time-record in a certain sea trial

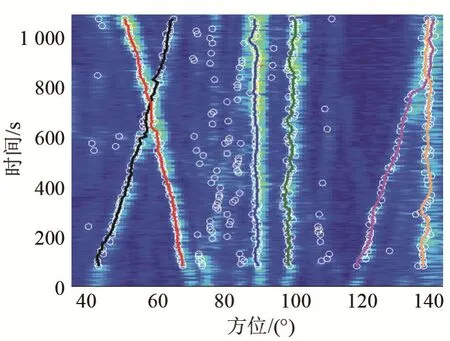
图5 BADA 算法关联跟踪结果Fig.5 Tracking results of the BADA algorithm

5 结 论

针对多目标跟踪中的数据关联问题，本文提出了一种基于蝙蝠算法的数据关联方法。将数据关联问题建模成组合优化问题，然后通过改进蝙蝠算法，使其可以适用于解决多目标跟踪中的数据关联问题，并且取得了较好的效果。该方法本质上是一种近似最优的方法。通过仿真结果可以看出，该方法在多目标、多杂波、多航迹交叉的情况下可以正确地关联目标，关联跟踪性能与JPDA 处于同一级别，运算复杂度迅速减小，实时性更好。通过对试验数据的分析，证明基于蝙蝠算法的数据关联方法应用于真实情况是切实可行的，并且有较好的关联跟踪效果。