压力衰竭地层地应力变化及影响因素

胡棚杰 李忠慧 赵毅 楼一珊 方满宗

1.长江大学石油工程学院；2.长江大学·油气钻井技术国家工程实验室防漏堵漏研究室；3.中海油能源发展股份有限公司工程技术湛江分公司

压力衰竭地层易发生井下事故。J.Geertsma(1973)［1］通过实验证明孔隙压力下降会导致地应力下降，J.Laurent (1993)［2］通过石灰石实验验证了孔隙压力变化会导致岩石Biot 系数变化，R.R.Hillis (2001)［3］研究证明孔隙压力降低会导致最小水平主地应力的降低，V.A.Dunayevsky 等(2010)［4］通过实验证明了压力衰竭会导致断层的活跃，梁何生等(2004)［5］在不考虑岩石弹性模量和泊松比变化的情况下推导出地应力随孔隙压力变化计算公式；刘向君等(2011)［6］通过岩石力学实验得到孔隙压力对岩石弹性模量、泊松比、抗压(拉)强度、黏聚力等影响显著，闫传梁等(2013)［7］通过对压力衰竭地层的井周应力分布规律分析安全钻井井斜角的变化规律；赵凯等(2017)［8］通过衰竭后地层应力变化研究确定了地层压裂起裂和延伸的变化规律，刘阳等(2018)［9］通过简化地层模型分析得到压力衰竭后安全钻井液密度窗口的变化规律。

笔者在平行地层考虑岩石力学参数的变化，运用广义胡克定律，建立地应力计算新模型，地应力的变化受多因素影响：油气压力、弹性模量、泊松比、原始地应力等，展现出水平主地应力在2 个方向上的变化不等，即油气压力下降后主地应力差会发生改变。在现场实际应用中，通过主应力差得到油气压力衰竭井段的有效剪应力变化情况，预测出4 处井漏高发点，其中3 处如期发生，表明本地应力计算模型对地应力的预测更准确。

1 压力衰竭地层地应力预测新模型

目前压力衰竭后地应力的计算模型［10-11］都是根据广义胡克定律推导出的，计算表达式如式（1）。

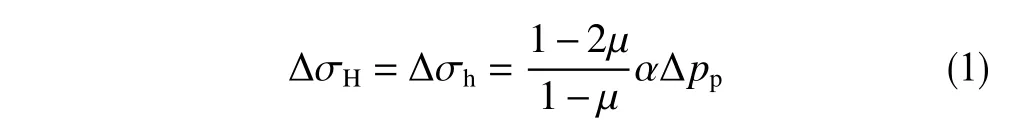
式中，ΔσH、Δσh为最大、最小水平地应力的变化量，MPa；μ为泊松比，无量纲；α为有效应力贡献系数，无量纲；Δph为地层压力变化量，MPa。

该模型仅考虑孔隙压力对地应力的影响，考虑因素过少，压力衰竭后地应力预测具有较大误差。压力衰竭后水平地应力的改变应与地层原始受力状态以及压力衰竭前后岩石特性参数有关，针对原有模型的不足，对其进行改进，假设地层岩石为横观各向同性弹性材料，则压力衰竭前地层岩石在地应力作用下的形变方程为

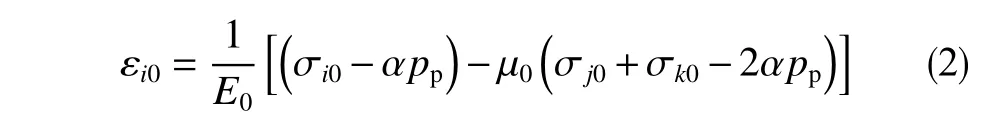
压力衰竭后地层岩石在地应力作用下的形变方程为

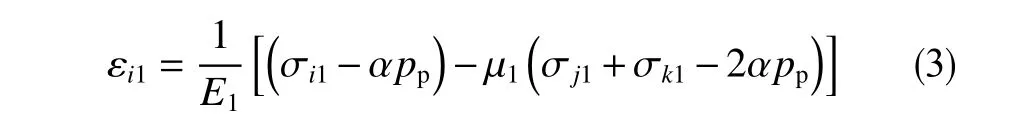
式中，ε为岩石形变，无量纲；μ为岩石泊松比，无量纲；E为弹性模量，MPa；α为应力贡献系数，无量纲；pP为孔隙压力，g/cm3；σ为地层应力，i、j、k分别代表空间直角坐标中3 个不同的方向，同时σx=σH(水平最大主应力)、σy=σH(水平最小主应力)、σz=σH(垂向主应力)。

地层压力下降后，基岩应力必然增加将导致岩石颗粒挤压变形，油气田地表会出现一定程度的下沉。但是下沉量一般远小于储集层埋深，可以认为上覆岩层压力在油气压力衰竭前后不变，即σv0=σv1=σv。同时由于致密圈闭层的存在，限制了岩石在水平方向上的变形，即εH1-εH0=εh1-εh0=0，建立了地应力计算模型［12］

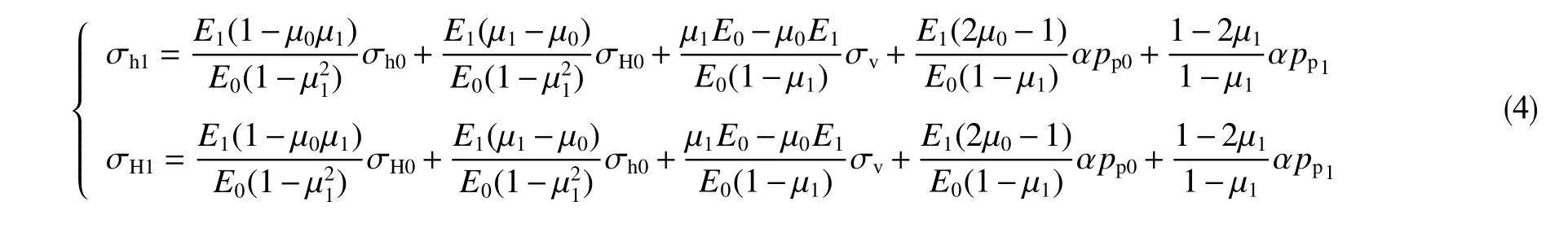
式中，μ为岩石泊松比，无量纲；E为弹性模量，MPa；σv、σH、σh为3 个主地应力；p为孔隙压力，g/cm3。

在本模型中当E1=E0、μ1=μ0时，式(4)即变成式(1)，即本模型变换成前人所推导出的地应力计算模型，因此前人推导的油气压力衰竭后的地应力计算模型为本模型的特殊情况，本模型更具有一般性。另外，压力衰竭后σH1与σh1的组成项中有3 个共同项，说明了孔隙压力pP、上覆岩层压力 σv对衰竭后水平地应力在2 个水平方向上具有同等影响力，其主要原因在于将岩层看作是横观各向同性材料。同时σH0、σh0系数相减得到，即σH0对压力衰竭后对地应力的影响权重高于σh0，压力衰竭后最小水平主应力的下降程度将会大于最大水平主地应力的下降程度。

2 地应力差变化规律

应力差与岩石的破坏之间有着紧密的联系：金衍等人(2008)［12］通过实验发现法向应力差的增大会促使水力裂缝穿透岩性突变体并继续沿着原来方向扩展。李勇明等人(2015)［13］通过实验得到高水平应力差会是水力裂缝更易穿过天然裂缝，刘玉章等人(2015)［14］通过软件模拟得到同样结论，可知压力衰竭后应力差增大易导致井壁处产生裂缝连通天然裂缝而导致井漏。通过本模型式(4)推导出法向应力差为式(5)，水平应力差为式(6)

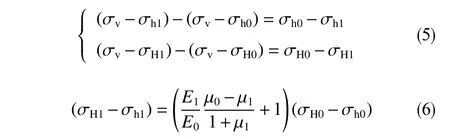
根据式(6)，得到应力差增量式(7)

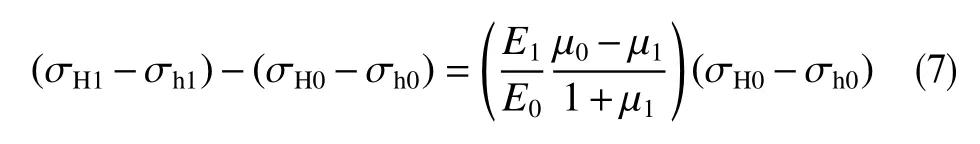
压力衰竭后岩石具有泊松比下降(μ1＜μ0)、弹性模量增加(E1＞E0)的一般性质，结合式(5)可知：压力衰竭之后水平地应力差会增大，应力差的增大程度主要与岩石泊松比与弹性模量的变化有关。

3 压力衰竭后裂缝面有效剪应力变化模型

假设在压力衰竭之前地层天然裂缝长为2a并且裂缝面平行于某一主地应力方向，裂缝所受地应力分别为σ1、σ2(σ1＞σ2)，裂缝面与σ1的夹角为α。通过对裂缝面的受力分析，裂缝面所受的正应力σn、剪应力τn见式(8)、式（9）

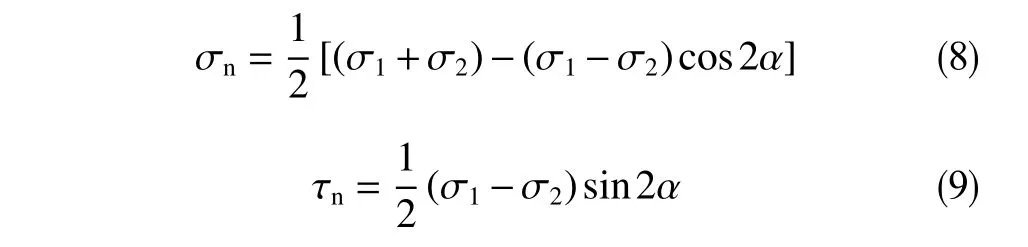
地层岩石受到三向压力，天然裂缝一般为闭合状态，则裂缝壁面会有摩擦力的存在，则裂缝面所受的有效剪应力为

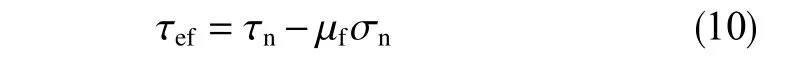
式中，μf为岩石内摩擦系数，无量纲。

式(8)、（9）代入式(10)，有

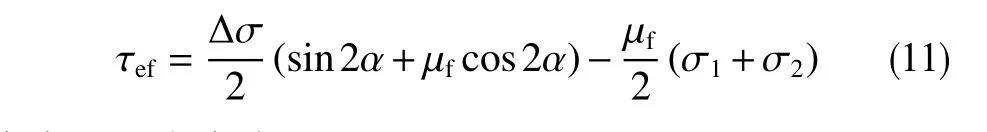
式中，Δσ为应力差，MPa。

4 应用实例

莺歌海盆地DF 气田于20 世纪末投入生产，气藏地质分层自上而下分别为第四系、莺歌海组、黄流组，储层为莺歌海组Y2 段Ⅲ气组，埋深1 235～1 275 m，平均孔隙度18%，有效渗透率约10×10-3μm2。开采初期储层与上部地层都属于正常压力系统，经过近20 年衰竭式开采，储层压力(当量密度)衰竭至0.46 g/cm3。储层原始及压力衰竭后水平地应力、有效剪应力变化见图1～图4。

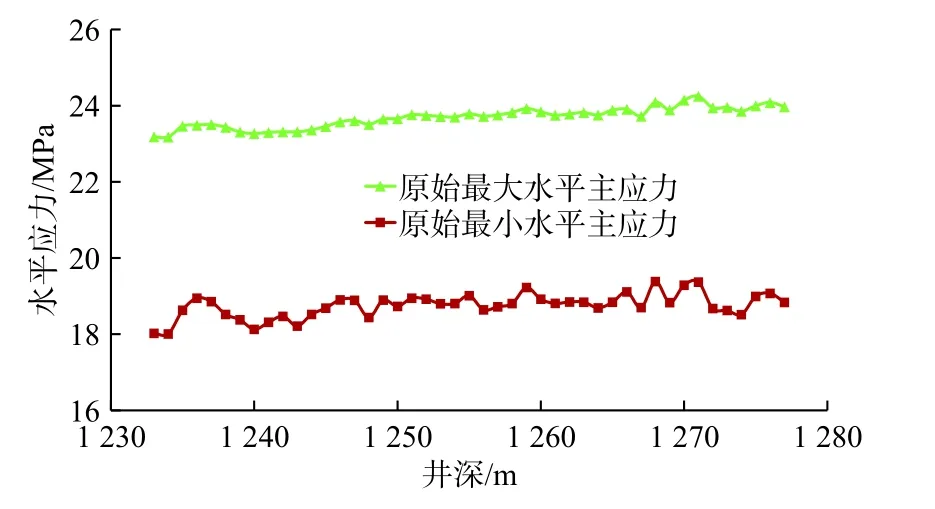
图1 原始水平地应力Fig.1 Original horizontal in-situ stress

从图2 中可以看出油气压力当量密度从1.03 g/cm3衰竭至0.46 g/cm3后，最小水平主地应力下降程度基本在19%左右浮动，最高达到20.5%，最低达到17%；最大水平主地应力下降程度基本在13%左右浮动，最高达到16.1%，最低达到7.5%；从数据上表明最小水平主地应力下降程度大于最大水平主地应力。同时在该图中2 条水平主地应力降低程度曲线变化趋势基本一致，主要原因在于本模型是基于岩层为横观各向同性材料；但变化幅度有着明显不同，主要原因是地层原始水平主地应力本就不相等，对于压力衰竭后地应力的变化表现出不同程度。

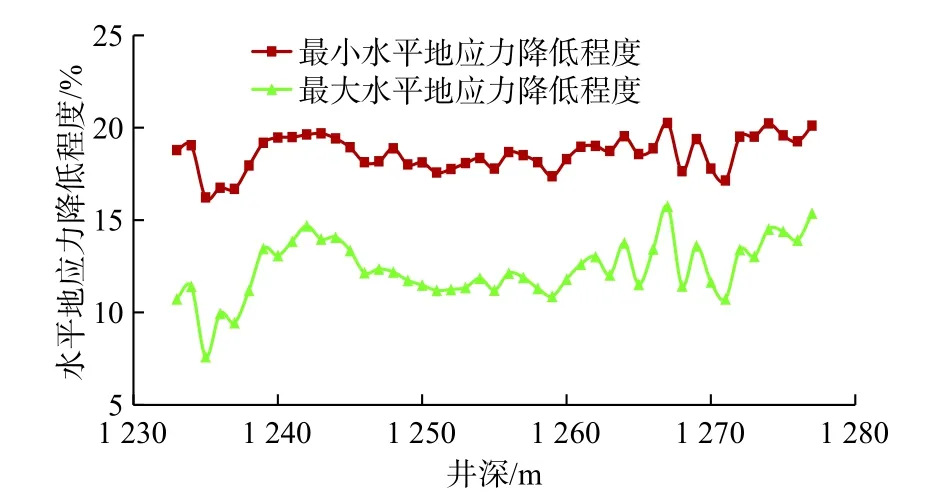
图2 压力衰竭后水平地应力降低程度Fig.2 Reduction degree of horizontal in-situ stress after pressure failure

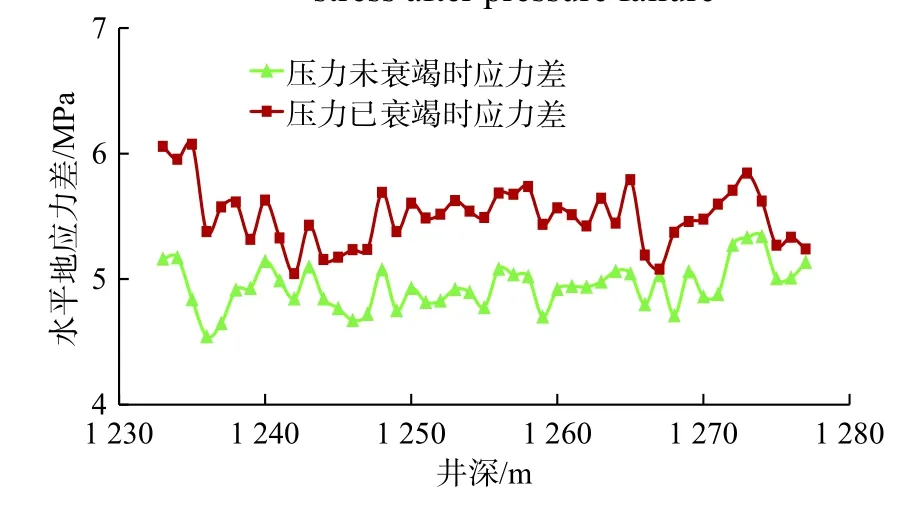
图3 衰竭后水平应力差变化Fig.3 Changes in horizontal stress difference after failure

从图3 中可以看出1 235～1 275 m 井段压力衰竭后应力差与原始应力差之间的差值最高达到1.24 MPa，平均值为0.56 MPa，可知油气压力衰竭后地层应力差增大明显。

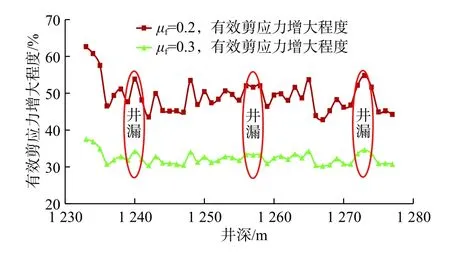
图4 衰竭后有效剪应力变化Fig.4 Changes in effective shear stress after failure

从图4 可看出当岩石内摩擦系数μf=0.2 时有效剪应力增大程度基本在50%左右浮动，而当岩石内摩擦系数μf=0.3 时有效剪应力增大程度基本在33%左右浮动。表明岩石内摩擦系数越小油气压力衰竭后岩石有效剪应力增大程度越大，即胶结越疏松的岩石压力衰竭后有效剪应力增大越厉害，发生井下复杂的概率越高。图中2 条曲线变化趋势基本一致，但变化幅度明显不同，内摩擦系数越小有效剪应力增大程度的波动越剧烈。同时在图中可以看出1 235～1 275 m 井段共有3 处有效剪应力突增点，均如期发生了井漏事故，表明本论文提出的地应力计算模型在现场应用中具有良好效果。

5 敏感性分析

本论文地应力计算模型对于比原有模型，压力衰竭后地应力受到弹性模量、泊松比的变化以及上覆岩层压力影响，为了探究弹性模量、泊松比的变化及上覆岩层压力对地应力的影响，采用单因素分析法进行敏感性分析，分析某一种因素时,保持其他因素不变。分析所用数据为第四部分实例应用数据。表1 为DF 气田地层原始数据统计。

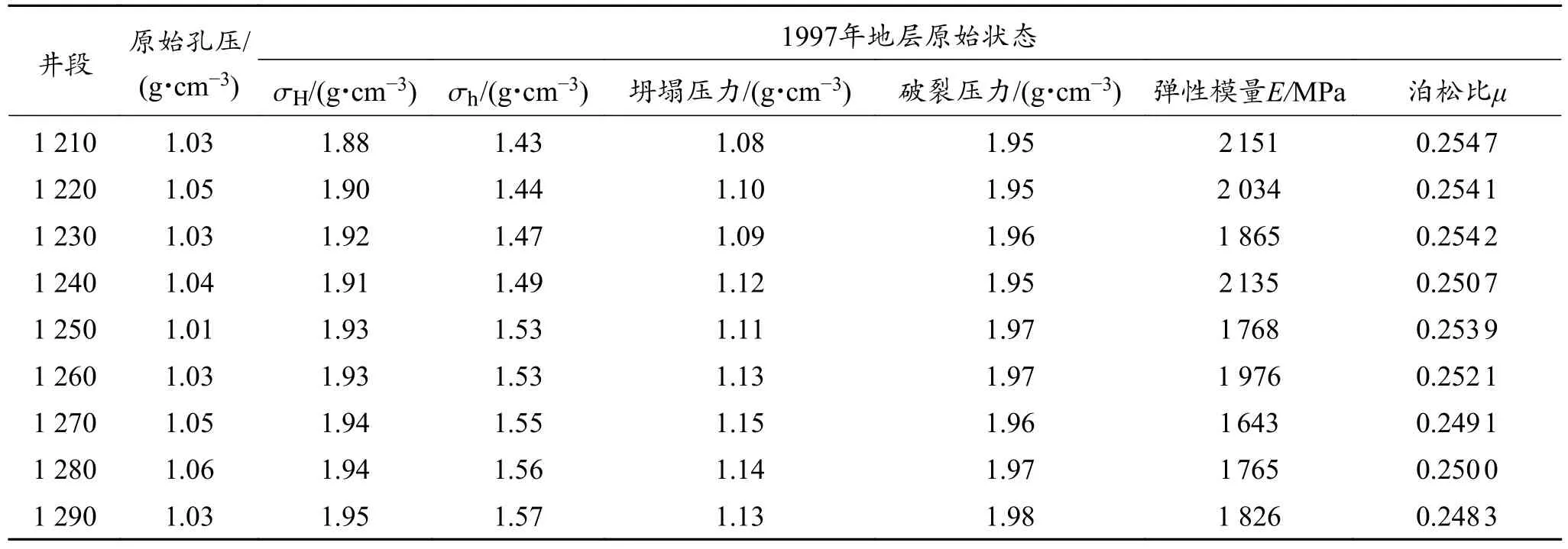
表1 DF1-1 井附近地层压力未衰竭时的地层实际状态Table 1 Actual state of formation near Well DF1-1 when formation pressure is not exhausted

5.1 弹性模量变化

当μ0=μ1=μ、pp0=pp1=pp时，图5 所示为不同弹性模量下对应的水平地应力值。当弹性模量增加5%时，最大水平主地应力平均增加1.598%，最小水平主地应力平均增加0.658%；当弹性模量增加15%时，最大水平主地应力平均增加4.793%，最小水平主地应力平均增加1.975%；当弹性模量增加25%时，最大水平主地应力平均增加7.989%，最小水平主地应力平均增加3.291%；当弹性模量增加35%时，最大水平主地应力平均增加11.185%，最小水平主地应力平均增加4.608%；当弹性模量增加45%时，最大水平主地应力平均增加14.391%，最小水平主地应力平均增加5.924%。可以看出，弹性模量的增大会导致水平地应力增加，但是最大水平地应力增大程度明显大于最小水平主地应力，说明弹性模量的增大会导致水平应力差的增大。从图5a可以看出弹性模量对最大水平主地应力的影响几乎不随井深而变化，但在右图中可以看出弹性模量对最小水平主地应力的影响随着井深的增加而加剧。

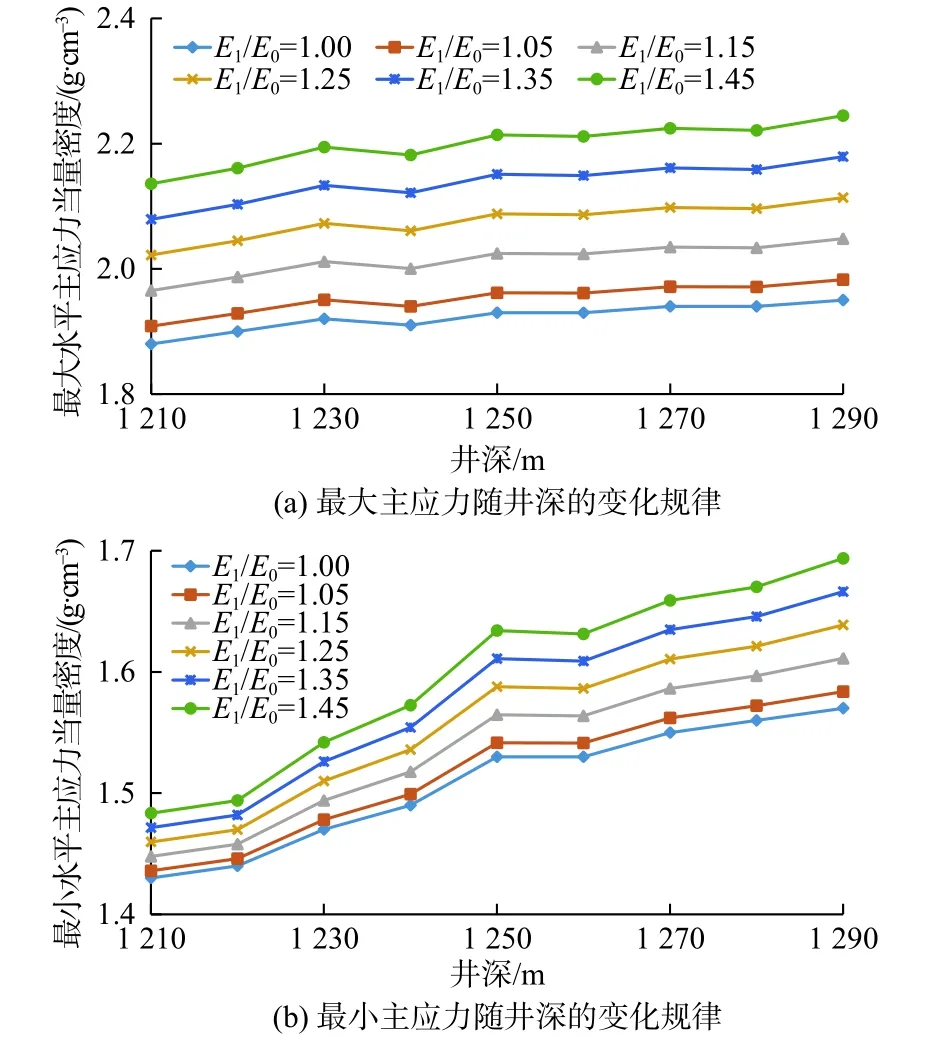
图5 不同弹性模量下的水平地应力Fig.5 Horizontal ground stress under different elastic modulus

5.2 泊松比变化

当E0=E1=E、pp0=pp1=pp时，图6 所示为不同泊松比下对应的水平地应力值。从图中可以看出泊松比的变化对水平地应力的影响不随井深而改变，同时泊松比每下降10%，最大、最小水平主地应力当量密度几乎都下降0.1 g/cm3；当泊松比每上升10%，最大、最小水平主地应力当量密度也几乎都上升0.1 g/cm3。因此，泊松比下降(或上升)，对水平地应力差几乎不产生影响。

6 结论

(1)当E1=E0、μ1=μ0时本论文建立的地应力计算模型即变成前人推导出的地应力计算模型Δσh=ΔσH=(1-2μ0)/(1-μ0)αΔp，可以看出前人建立的模型为本模型的特例，本模型更具有一般性。

(2)根据本模型解释，孔压降低之后最小水平主地应力降低值大于最大水平主地应力，水平地应力差增大。通过岩石有效剪应力来验证其预测地应力效果，预测结果与实际现场相符。

(3)压力衰竭后岩石所受有效剪应力增大明显。将本文模型应用于SF1-1 井并与该井实际钻井情况结合分析发现：有效剪应力突增点井壁不稳定，易发生井漏事故。压力衰竭地层井壁有效剪应力可作为判断该井段是否易发生井漏的依据之一。

(4)岩石弹性模量的增加会导致水平地应力差的增大，且其对最小水平主地应力的影响随井深的加深而变大；泊松比对水平地应力的影响几乎相同，不会导致水平地应力差的变化。