基于生成式对抗网络的中国电影连续观影数据预测①
姜禄瑶,曲丽萍
1(上海市崇明区融媒体中心广播电视部,上海 202158)
2(上海大学 上海电影学院规划办公室,上海 200444)
1 引言
近年来,中国电影市场迅速发展,无论其银幕数量还是票房收入均逐年上升.2017年,中国电影市场的票房收入达到559.1 亿人民币,正式成为仅次于北美的全球第二大电影市场.同时,2017年中国电影银幕数量新增银幕9597 块,总共达到50 776 块,稳居世界电影银幕数量第一位.
在电影上映过程中,观影数据可以体现观众对于相关电影的评价,以及这些观众向他人推荐该电影的倾向.因此,实时观影数据与电影最终的票房及观众评分均高度相关[1].在电影上映过程中,合理的挖掘和分析实时观影数据有助于电影营销方了解观众动向,从而有针对性的调整影片营销和发行的战略.其中,准确的预知电影上映时期票房,观影人数和其它观影数据的走势将能为电影营销,院线排片等提供有效的指导和帮助,提升电影单场平均上座率和场均收益.近年来,得益于机器学习技术的快速发展,电影票房预测模型被广泛提出和应用.Hossein 等[2]利用86 部电影上映前四天的动态推特数据作为特征,并利用多种机器学习模型对电影票房进行预测.文献[3]对用户评论进行分析,提取其中的情绪信息作为特征,并利用非线性回归器,如:决策树,人工神经网络,支持向量机等对票房收入进行评估.文献[4]利用特征交叉组合网络和稠密跳接网络对电影上映前信息进行深度特征提取,并预测上映后的票房.文献[5,6]均利用机器学习算法对电影周边信息进行分析,并预测电影票房.
上述研究虽可通过社交数据,演员信息,电影类型、上映日期等电影上映前的信息来预测电影观影数据,却忽略了电影上映时期实时变化的动态信息(dynamic information),因此目前仅应用于电影总票房预测,而非每日票房预测.文献[7]虽然利用深度神经网络(DNN)对电影每日票房进行预测,但仍未使用实时动态信息.
目前,许多动态信息编码算法,如LSTM,马尔科夫链等被提出和应用在各个预测领域,例如:车辆轨迹预测[8]以及与本文目标类似的金融数据预测[9]等,并取得了优异的效果.
在电影数据分析中,动态信息可以有效表征和编码由电影上映时期不可控因素(如主要演员违法,国家出台新政策等)对各观影数据所带来的影响和变化.在文献[10]中,作者基于高斯混合模型(Gaussian Mixture Model,GMM)对电影上映首日的数据进行分析.其研究结果表明,每日票房均对下一日票房具有显著影响,利用该信息可有效提高预测精度.因此,相对于仅利用电影上映前的静态信息,同时分析上映前的静态信息和上映时期的动态信息来对电影观影数据进行预测将理论上取得更精确的结果.为了有效利用电影上映时期的动态信息,本文提出一种基于傅里叶变换的动态信息编码算法.该算法将已上映日期的动态数据(由于已上映日数的差别,原始数据的长度将不同)编码至一对大小固定的频谱图中,作为后续特征提取器和分类器的输入.
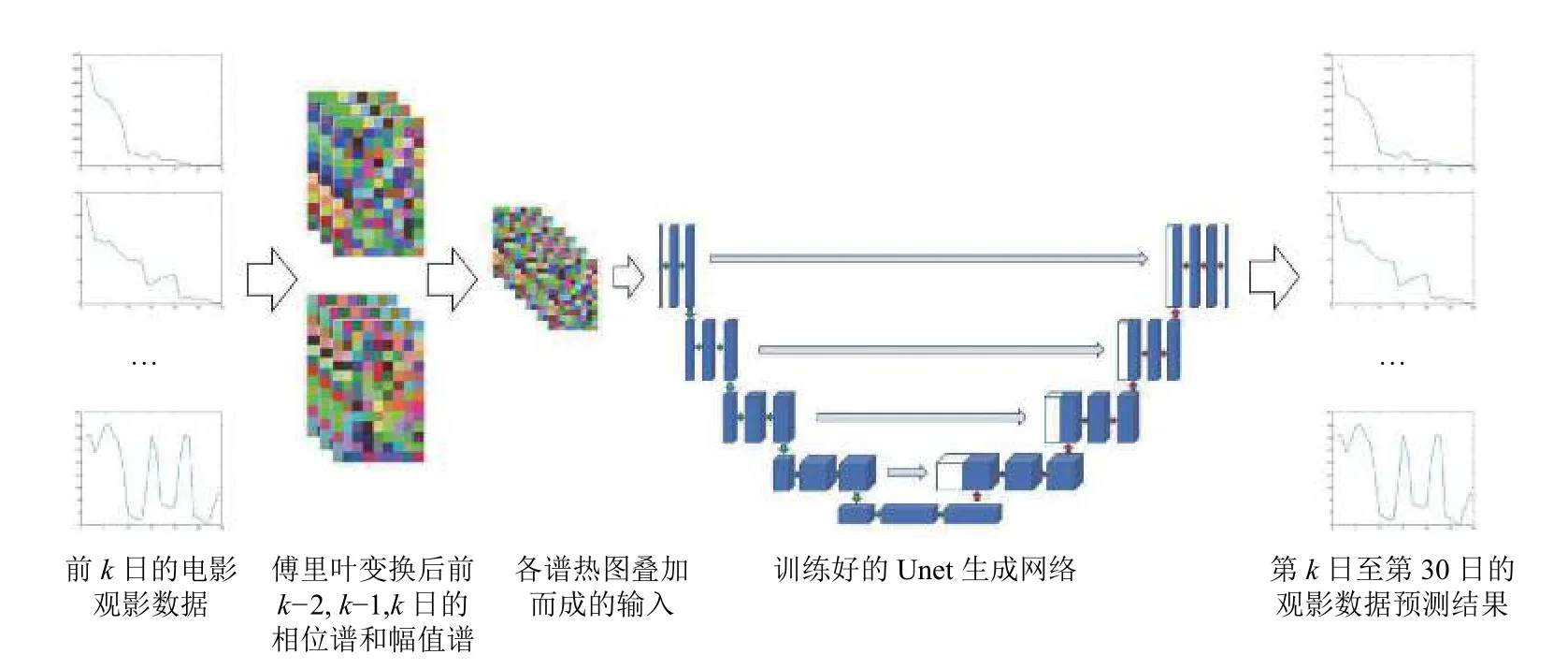
生成式对抗网络[11]是一类近年来被广泛应用[12]的深度学习模型,其思想是通过学习生成器的生成能力和判别器的判别能力,优化寻找二者的纳什均衡.由于生成式对抗训练算法(generative adversarial training)在近年来显示出的优异的性能,生成式对抗网络被改进并应用到多种生成和预测任务中,如图像翻译(imageto-image translation)[13],图像修复[14],行为预测[15,16]等.虽然该类方法在计算机视觉各领域取得了成功,然而其在电影观影数据分析上的应用却未被系统的研究.考虑到本文的目标为利用给定日期的电影观影数据预测余下日期的电影观影数据,其输入和输出均为矩阵形式,与图像翻译类似.因此,本文基于生成式对抗网络(GAN)对电影观影数据进行预测.该系统的总流程如图1所示.

图1 本文算法流程图
2 相关工作
2.1 傅里叶降维算法
傅里叶变换(Fourier Transform,FT)是一种线性积分变换,可将时间信号转换到频率域.转换后的频谱信号将时间信号分解为一个基波和多个谐波的和,从而可获得时间信号各个同频率范围内的信号强度,其定义如下:
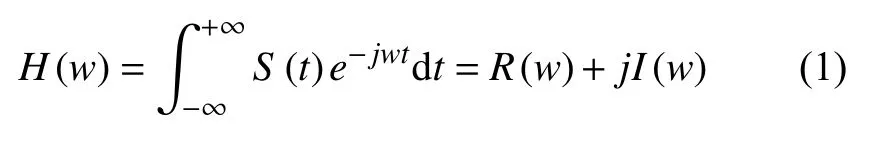
其中,S(t)为初始时间信号,H(w)为转换后的频谱信号.在实际应用中,由于时间信号一般为离散且长度有限的序列,因此之前大部分时频转换算法采用离散傅里叶变换(Discrete Fourier Transform,DFT)对时间信号进行处理.如图2所示,假定离散时间信号S(t)长度为n帧,则其进行离散傅里叶变换后的频谱信号可表示为:

其中,N为频率点采样个数.通过控制参数N,文献[17,18]提出了一种时间信号降维算法.当利用DFT 处理长度不同的时间信号时,其将频率点采样个数设置为相同的值N从而使得转换后的信号具有相同个数的谐波分量.其中,各谐波分量的幅值M(k)和相位信息P(k)(k=0,1,2,···,N–1)可通过式(5)和式(6)计算获得.
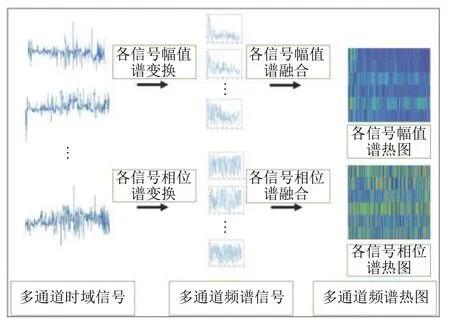
图2 傅里叶降维算法[18]
因此,不同长度的离散时间信号均可转换为两个长度为N的一维信号(N个幅值和N个相位值).相比于降采样和重采样法会使得信号发生畸变,直方图法导致信号动态信息丢失,该算法的优势在于:①可在大幅缩减信号长度,以利于基于CNNs的全局特征的提取;②可将不同长度的信号转化为同样长度的;③同时保留信号幅值信息(幅值)和上下文动态信息(相位),同时保持这些信息不发生畸变.
2.2 生成式对抗网络
生成式对抗网络(Generative Adversarial Networks,GAN)于2014年由Goodfellow 等[11]提出,是一种非监督学习方式.该类网络一般由两个卷积神经网络组成:生成网络和判别网络.生成网络对原始输入进行特征提取和重建以生成与训练集中目标尽可能类似的输出,以欺骗判别网络.与此同时,训练集中的真实样本和生成样本将用于训练判别网络,使得该网络可以尽可能地区分真实样本和生成样本.两个网络在训练过程中将进行多轮博弈,对抗,同时不断调整各自参数.该过程的最终目的是使得生成网络的性能达到极限,使得由其生成的样本可以最大限度地欺骗已经训练好的,性能已达极限的判别网络,让其难以区分真实样本和生成样本.
3 预测模型
基于上述傅里叶降维算法和生成式对抗网络,本文提出一种电影实时观影数据预测算法.针对指定电影,该算法根据已上映各日的电影票房,上座率,排片量等公开信息预估之后各日的上座率,票房等.首先,算法将基于傅里叶降维算法对电影已上映日各信息进行预处理,将其由多通道时域信号转化为固定大小的多通道频谱信号.然后,基于生成式对抗网络对转换后的信号进行动态深度特征提取,并对后续日期的电影数据进行预测.本文算法框架如图1所示.
3.1 数据预处理
在一般情况下,卷积神经网络的输入层尺寸保持固定,因此训练和测试样本数据的尺寸也需通过预处理使其保持一致.由于电影数据的尺寸会根据已上映日数的改变而发生变化,本节首先将各部电影不同日期的数据进行转换,以保证各个数据尺寸大小一致.
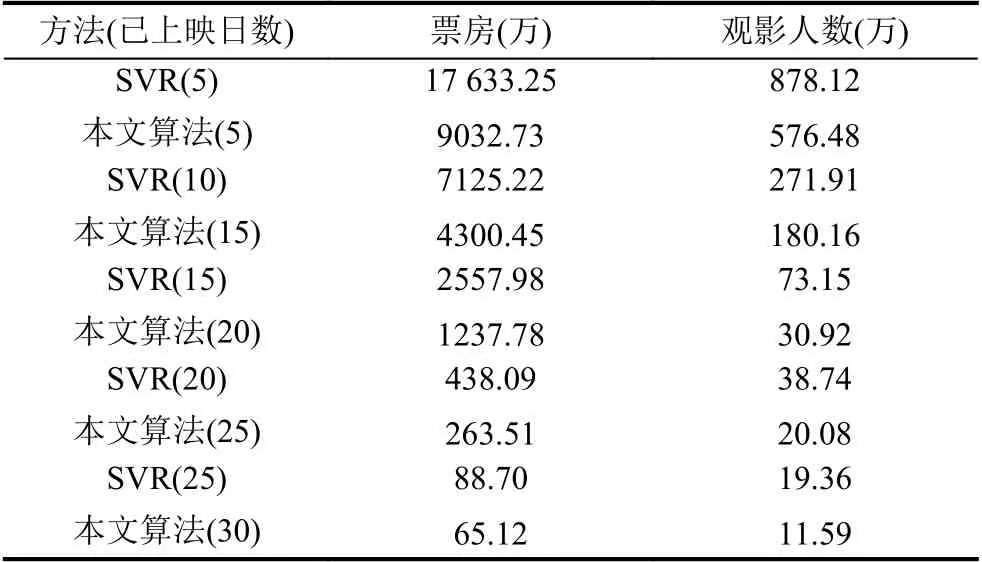
假设给定电影的数据包含n日信息,每日信息维度为k维,则该数据等同于通道数为k,帧数为n的多通道时间信号.如图2所示,通过将上述傅里叶降维算法的采样点数设置为N(N 相比于传统手工特征,卷积神经网络可以根据任务目标对提取输入信号的最优特征,从而在近年来许多模式识别任务上都取得了更好的效果.因此,本文利用卷积神经网络对转换后的频谱数据提取深度特征. 虽然上述转换后的频谱信号已经包含原始信号全局的幅值和动态信息,但却无法提供其中一小段日期的动态信息.考虑到在一般情况下,每日的上座率和票房均与前一日和后一日的相应数据有着紧密的联系.因此,在一般情况下,已上映日中最后几日的观影数据的动态信息将与待预测数据有着最紧密的联系.为了提取这几日的局部动态信息,本文同时将多日的数据频谱图进行编码作为卷积神经网络的输入以提取深度动态频谱特征.假设给定电影的数据包含n日信息,d(1,t)为给定电影从上映第1日至第t日多通道电影数据(t≤n),为了获取动态特征,连续k日的信息d(1,n),d(1,n–1),···,d(1,n–k+1)将基于公式被转换为2k个大小为频谱热图(k个幅值谱热图Am(1,n),Am(1,n–1),···,Am(1,n–k+1),k个相位谱热图Ph(1,n),Ph(1,n–1),···,Ph(1,n–k+1)). 其中,f(1,n)为给定电影从上映第1日至第n日的动态深度频谱特征. 在将高维的电影频谱数据进过特征提取转换为低维的深度特征之后,本文通过再次通过卷积神经网络(G)对得到的低维特征进行反卷积以此预测后续日期的电影数据,其过程可表示为公式: 其中,d(n+1,30)为预测得到的,从第n+1日至第30日观影数据,f(1,n)为作为输入的已上映日期的观影数据.为了提取多层次信息,本文利用Unet 深度网络[19]进行深度特征提取(f)和数据预测(G).Unet 于2015年提出,并在图像分割上取得了优异的效果.Unet 结构简单,且可以提取多层次特征,因此被成功用于图像动态信息(temporal modeling)预测[15].同时,由于生成式判别网络在预测任务中的良好效果,本文利用类似结构对电影观影数据进行预测.其中,生成网络为修改后的Unet,其需要优化的参数数量为7.3 M.同时,由于Residual Network 目前在多个公开的图像分类数据集上均取得优异的分类效果,因此本文选择的的判别网络为Residual Network 101[20].其参数量为42.6 M.该网络使用单个12 G GPU 完成训练时间大约为5 小时. 在训练时,Unet 首先将输入的动态频谱数据进行编码,并生成预测数据.接着,该预测数据将输入Residual Network 进行分类,若判别为假,则Unet 将继续训练,直到其生成的数据被Residual Network 判别为真.此时,我们再利用生成数据和真实数据对Residual Network进行训练,直到其能判别出生成数据为假.根据该方式训练多轮后,直到Residual Network 无论如何训练都无法判别生成数据为假时,训练停止,并利用此时的生成网络进行数据预测. 本文所提出的算法具体步骤如图3所示.假设原始数据包含前k日的观影信息,算法首先将编码后的频谱数据输入生成网络进行特征提取和第k+1日到第30日的观影数据生成.接着,将生成网络的输入(编码后的频谱数据)和输出(生成的观影数据)基于公式X进行配对后得到的数据将为一个包含X层的二维矩阵组VF.该步骤的目的是为判别网络提供限制条件,使其能根据生成网络的输入来对预测数据进行判别,从而避免训练好的生成网络错误收敛,使其在不同输入时的输出为一个相同的电影观影数据.在训练过程中,包含生成数据的二维矩阵组的标签为0.同时,本文将真实的第k+1日到第30日观影数据与对应的编码后的频谱数据基于公式X进行配对得到VT,并将其标记为1.之后,利用所有标记好的真实数据和生成数据对判别网络进行训练.在生成式判别网络的训练过程中,生成网络和判别网络会相互博弈,调整各自的参数,使两者性能都不断提升.因此,训练完成后的生成网络将具有良好的预测性能. 图3 预测算法框架 为了验证所设计模型的预测效果,本文收集了近三年在国内上映的电影数据进行分析.该电影集包含2018年国内票房前60,2017年票房前70和2016年票房前70的共200 部电影.对于每部电影,其上映前30日内的15 种信息被统计,包括:上映日期,上映日数,排片占比(%),观影人次(万),人次占比(%),场均人次(个),平均票价(元),排座总量(万),排座占比(%),上座率(%),用户退票率(%)和是否法定节假日.其中最后一项中的法定节假日定义为周末和国家公共假日,其值为0 (非法定节假日)或1 (法定节假日).一般情况下,由于节假日观影人数较工作日有着显著上升,因此该信息对电影观影数据有着巨大影响.在本文实验中,200 部电影信息被分为3 个不重复的子集.其中训练集(training set)包含100 部,用于训练网络;验证集(development set)包含40 部,用于调整网络的超参数(hyper-parameters);剩余60 部组成测试集(test set),用于展示模型效果.为了方便广大学者,该数据集已经公开,可通过链接进行下载(https://drive.google.com/drive/folders/1NhZtK601 JSbTzX5kR060qkiKOd58gq5?usp=sharing). 本文利用3 种常用于时间信号的度量方式来计算预测值与真实值的相似度:均方误差(Mean Square Error,MSE),皮尔逊相关系数(Pearson Correlation Coefficient,PCC)以及相对误差.均方根误差用于度量预测值xi与真实值yi之间差异程度,其定义如式(7)所示: 在本文实验中,i代表第i日,i的值固定为30.与此同时,皮尔逊相关系数定义为: 其中,X为预测的时间信号,Y为真实的时间信号,cov(X,Y)为两者的协方差,σX和σY分别为两者的标准差.而相对误差定义为: 本文利用修改后的Unet 提取深度频谱特征和电影观影数据预测.在训练中,该网络利用随机梯度下降(Stochastic Gradient Descent,SGD)法对参数进行优化,其中学习速率为0.005,学习速率衰减为0.000 01,冲量(momentum)为0.5.与此同时,本文采用Residual Net 作为分类器,其同样利用随机梯度下降法对网络参数进行优化,其中学习速率为0.001,学习速率衰减为0.000 01,冲量为0.9. 实验结果如表1所示,表中所示为各日预测结果的平均值.当仅给定前5日数据时,4 个指标的后25日的预测结果平均相对误差均较大,分别达到26.8%,23.0%,17.0%和19.6%.而当获取前15日数据或更多日期的数据后,本文算法对未上映日期的观影数据预测能力将较为精确且趋于稳定,其预测误差均接近甚至小于10%.图4为基于动态算法的电影“侏罗纪世界”的预测结果示例. 为了验证本文算法对于给定日期不同情况下的适用性,表2比较了5 种不同情况下本文算法的预测效果,分别为:(1)给定各部电影前5日观影数据,预测各电影之后25日的观影数据;(2)给定各部电影前10日观影数据,预测各电影之后20日的观影数据;(3)给定各部电影前15日观影数据,预测各电影之后15日的观影数据;(4)给定各部电影前20日观影数据,预测各电影之后10日的观影数据;(5)给定各部电影前25日观影数据,预测各电影之后5日的观影数据. 为了比较本文动态算法与传统静态算法的优劣,表2展示了由本文方法预测得到的观影数据结果和仅用静态数据预测得到第k日后的总票房或总观影人数预测结果.其中,用于预测静态数据包括:导演获奖次数,男女主角的人气(国内演员定义为百度贴吧粉丝数,国外演员定义为Twitter 粉丝数),男女主角的获奖次数等.最后利用支持向量机(Support Vector machine Regression,SVR)对这些数据进行学习和预测.其具体算法可参考文献[21].根据结果可知,相比于利用静态数据进行预测,本文所提出的动态算法预测效果显著提升.相对于使用静态数据,在各个预测实验中,使用动态算法使得预测误差均下降超过45%.其中,在预测上映15日至第30日的总票房和总观影人数时,利用动态算法所得到的结果误差分别下降高达51.6%和57.7%. 表1 日观影数据预测平均结果 图4 侏罗纪世界观影数据预测结果示例 针对当前电影观影数据预测方法未利用上映时动态信息的缺点,本文提出一种基于生成式对抗网络的电影观影数据预测算法.该算法首先提取各电影已上映日期的15 种数据构成基本特征向量,然后利用傅里叶变换对这些特征向量进行动态编码.最后利用生成式对抗网络对编码后的频谱图进行分析,从而预测和生成未上映日期的电影观影数据.实验结果表明,本文提出的预测算法相对于基于静态数据的预测算法精度显著提升.由于训练数据数量所限,本文暂时未使用更加复杂的深层次网络结构,因此预测效果仍有提升空间.未来的工作将着重于采集更多相关数据,并设计更加适合用于观影数据预测的深度网络. 表2 预测算法MSE 对比3.2 动态频谱数据编码

3.3 上座率和票房预测
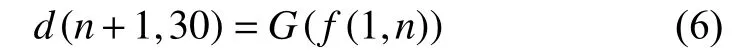
4 实验
4.1 数据库
4.2 实验设定
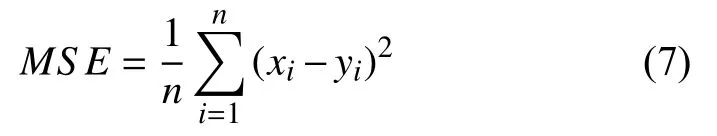


4.3 实验结果


5 结束语